双解析函数的一个带共轭值的边值问题

曾 伟

(西南民族大学预科教育学院，四川 成都 610041)

双解析函数的一个带共轭值的边值问题

曾 伟

(西南民族大学预科教育学院，四川 成都 610041)

讨论了双解析函数的一个带共轭值的边值问题.首先通过双解析函数的plemelj公式，把所要解决的边值问题转化为一类积分方程的形式.然后证明了几个有用的不等式，再结合函数论知识中的积分方程理论和压缩映像原理，得到了该问题的解的存在性和唯一性.

双解析函数;plemelj公式;积分方程理论;压缩映像原理.

设G是复平面上的一个区域，w(z)是G上的一个复函数，它具有关于的二阶导数.如果在G上，我们有=0，则称w(z)是G上的双解析函数.

在文［5］中，赵桢老师给出了双解析函数的定义，证明了一个双解析函数能够用解析函数唯一的表示出来，并且初步研究了双解析函数.在文［6－8］中，王明华和曾伟分别研究了双解析函数的相关性质，并讨论了双解析函数的几个边值问题.本文将在上述内容的基础上，研究双解析函数的一个带共轭值的边值问题.

本文将研究双解析函数w(z)的一个边值问题:

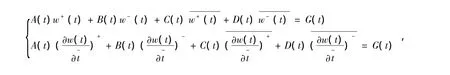
称它为条件R.

1 准备工作

命题1:(双解析函数的Cauchy积分公式)设D为复平面的有界区域，其边界D=L，由有限条光滑闭曲线组成.w(z)是D内的双解析函数，且w(z)∈，则

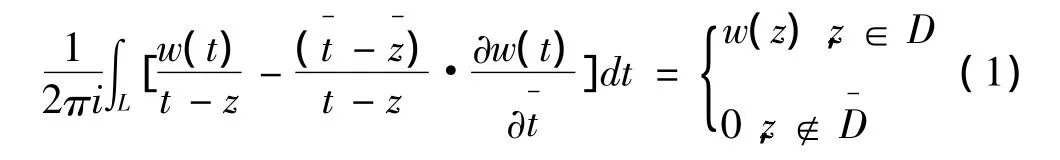
设L是一条光滑曲线，f1(t)，f2(t)是定义在L上的绝对可积复函数，定义Cauchy型积分如下:

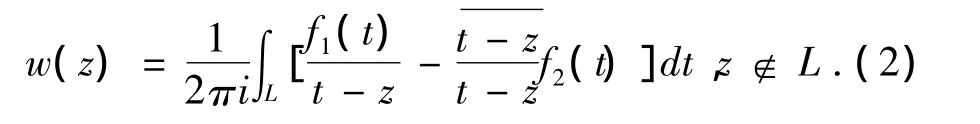
显然，w(z)在L外双解析.

命题2:(plemelj公式)

设L是一条光滑的Jordan闭曲线，D+，D－分别是D的内部和外部区域，f1(t)，f2(t)是定义在L上满足Ho¨lder条件的复函数，则当z分别从D+，D－趋近于t0(t0∈L)，有极限值且极限值为:

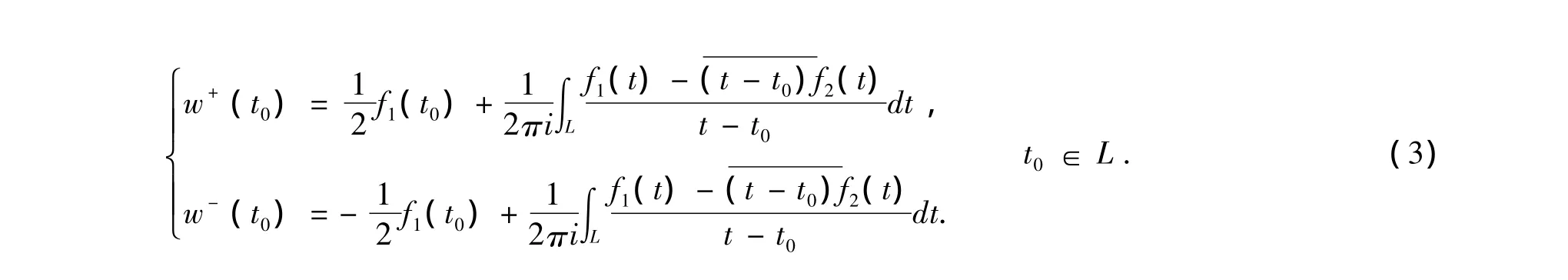
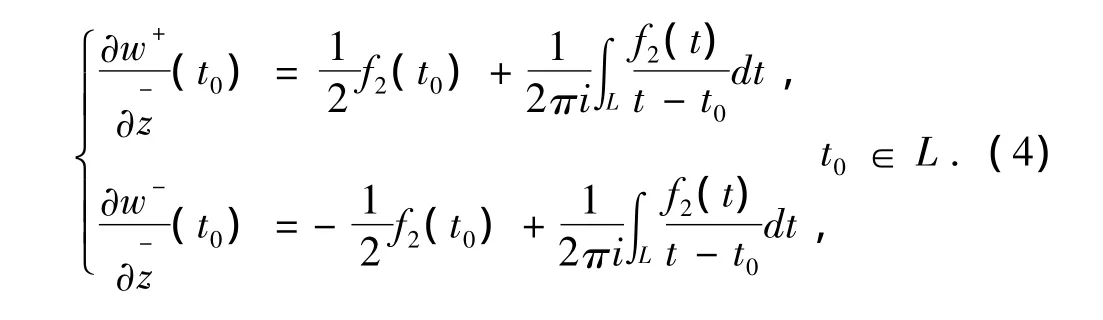
2 问题的转化

设A(t)，B(t)，C(t)，D(t)，G(t)是D的边界L上的已知函数，要找一个函数w(z)，使它在L上满足条件R，在L外双解析.显然由(3)式和(4)式可知，条件R可以转化为:

其中，

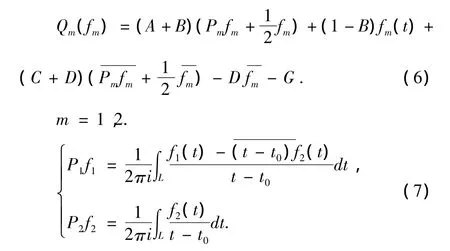
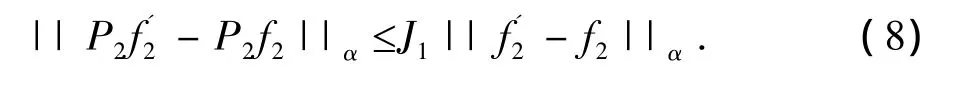
和

(2)提供制作平台。创客空间为创客提供从创意产生到实物制作所必须的工具设备。随着3D打印技术的成熟，开源硬件的兴起，使得不依托大型工厂，在社区、家里制作产品成为可能。不同技术领域的创客空间，还可根据具体项目加配相应的工具。

那么，

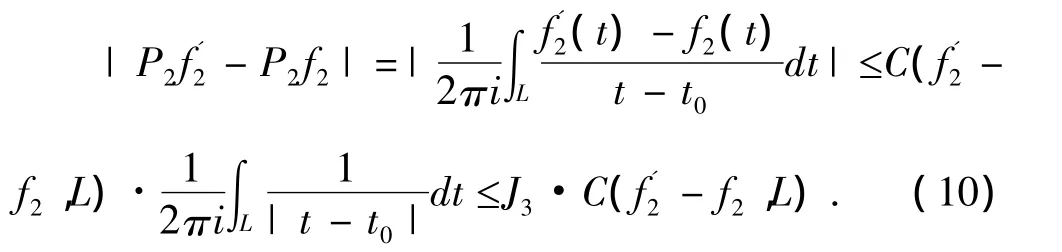
并且

则，仿照文［9］中的定理1的证明，我们有

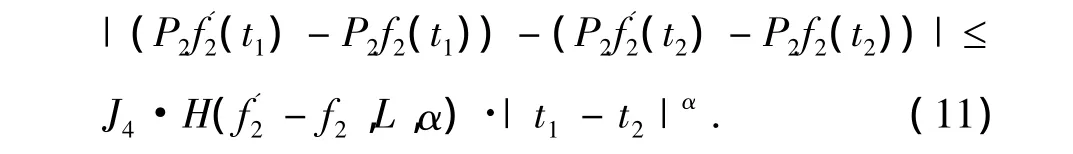
由(10)，(11)式，并且取J1=max{J3，J4}，则(8)式成立.

而对于(9)式，

由(8)式可知，取J2=J1+J5，则(9)式成立.

定理 2:设f2(t)∈H(L，α)被取定，且(t)，f1(t)∈H(L，α)，那么:

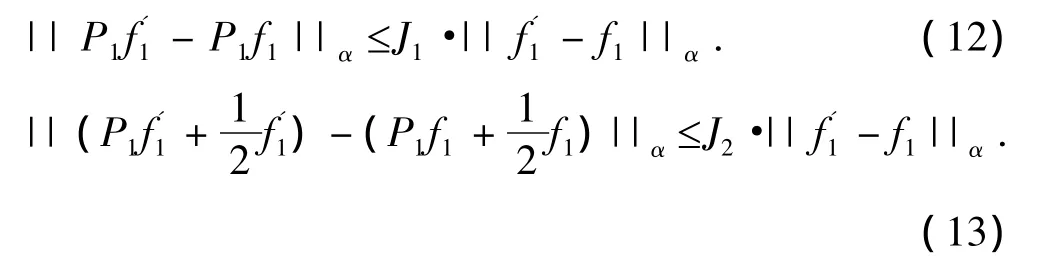
证明:由(7)式可知，

显然，由(8)(9)式可知，定理2成立.

定理3:在定理2的条件下，以下两个不等式成立

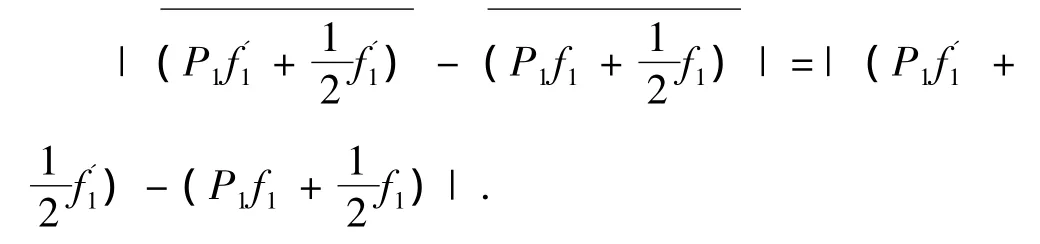
所以，仿照定理1的证明，易得定理3成立.

3 问题R的结果

定理 4:如果A(t)，B(t)，C(t)，D(t)∈H(L，α)，且r=J2(||A+B||α+||C+D||α+||1－B||α+||D||α)，那么当r＜1时，问题R中的第2个方程有唯一解.

证明:因为f2(t)，f'2(t)∈H(L，α)，那么

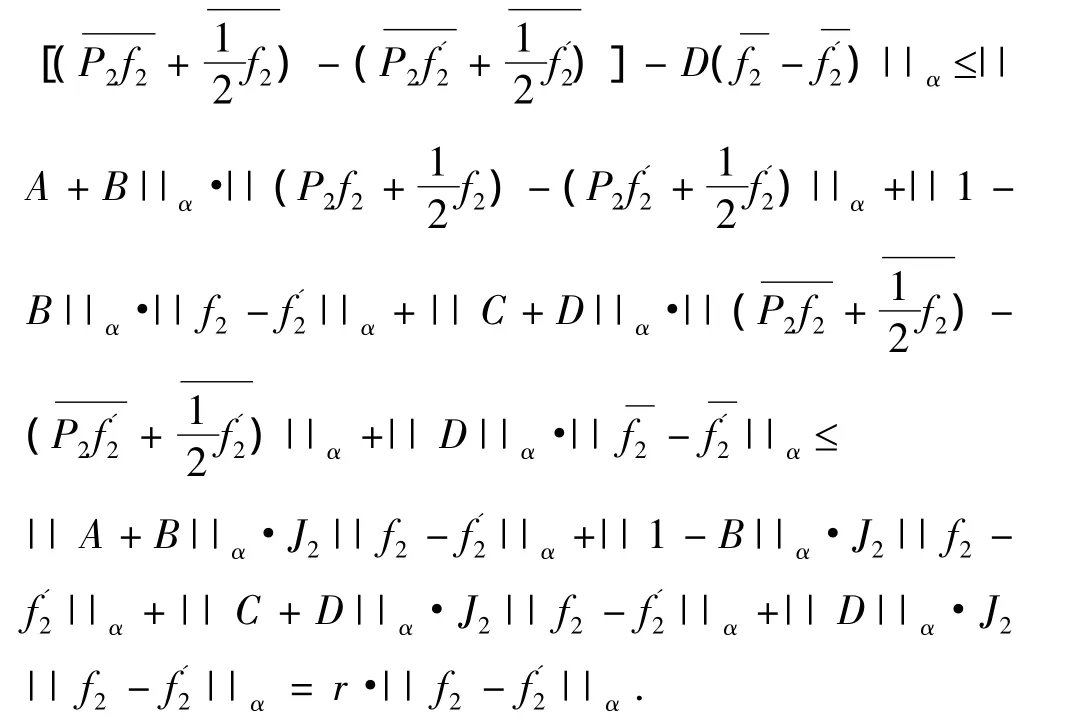
因为r＜1，所以由压缩映像原理，问题R中的第2个方程有唯一的一个解，记为f2(t).

定理5:在定理4的条件下，且f2，f1是取定的函数，那么问题R中的第1个方程有唯一解.

证明:

因为r＜1，所以由压缩映像原理，问题R中的第1个方程有唯一的一个解，记为f1(t).

定理6:在定理4的条件下，问题R的解存在并且唯一.

证明:由定理4和定理5的结果直接得证.

本文所得的定理，推广了文献［6－8］的结论，使得双解析函数的研究结果更加完善.下一步我们将研究双解析函数在双曲复数中的某些边值问题.

［1］维库阿·依·涅.广义解析函数［M］.中国科学院数学研究所，译.北京:人民教育出版社，1960.

［2］闻国椿.共形映射与边值问题［M］.北京:高等教育出版社，1985.

［3］路见可.解析函数边值问题［M］.上海:上海科学技术出版社，1987.

［4］李子值.函数论的边值问题［M］.河北:河北大学出版社，2000.

［5］赵桢.双解析函数与调和函数以及它们的基本边值问题［J］.北京师范大学学报:自然科学版，1995，61(2):175－179.

［6］王明华.双解析函数的性质及Hilbert边值问题［J］.北京师范大学学报:自然科学版，1998，34(1):13 －20.

［7］曾伟.无穷直线上双解析函数的一类非正则型边值问题［J］.西南民族大学学报:自然科学版，2013，39(4):554－559.

［8］曾伟.无穷直线上非齐次2阶方程=f的Riemann边值问题［J］.西南民族大学学报:自然科学版，2014，40(3):394 －198.

［9］黄沙，焦红兵，乔玉英，等.Clifford分析中的多个未知函数的非线性边值问题［J］.数学学报，1998，41(6):1185 －1192.

［10］杨丕文.k－正则函数及其某些边值问题［J］.四川师范大学学报:自然科学版，2001，24(1):5 －8.

［11］杨丕文.正则向量函数及某些函数论性质［J］.四川师范大学学报:自然科学版，1999，22(4):359－364 .

［12］杨柳.k－正则函数的性质及其Riemann边值问题和它的反问题［J］.四川师范大学学报:自然科学版，2005，28(1):39 －42.

［13］赵桢.双解析函数与调和函数以及它们的基本边值问题［J］.北京师范大学学报:自然科学版，1995，61(2):175－179.

［14］曾伟.k－正则函数的某些性质及其共轭k－正则函数的Riemann边值问题［J］.西南民族大学学报:自然科学版，2009，35(2):210－217.

［15］曾伟.k－正则函数的非正则型Riemann边值问题［J］.四川师范大学学报:自然科学版，2007，30(3):291 －294.

A boundary value problem with conjugate value for bianalytic functions

ZENG Wei
(School of Preparatory Education，Southwest University for Nationalities，Chengdu，610041，P.R.C.)

This paper discusses a boundary value problem with conjugate value for bianalytic functions.With plemelj formula，the problem is translated into an integral equation，and then，the existence and the uniqueness of the solution for this problem are proved by using the theory of integral equations and the contract mapping theorem.

bianalytic function;plemelj formula;theory of integral equations;contract mapping theorem

O175.2

A

2095-4271(2015)06-0741-04

10.11920/xnmdzk.2015.06.016

2015-06-30

曾伟(1980－)，男，四川成都人，讲师，研究方向:复偏微分方程的边值问题.Email:zw0830@163.com

中央高校基本科研业务费专项项目(2015NZYQN39)

(责任编辑:付强，张阳，李建忠，罗敏;英文编辑:周序林)