利用插值型无单元Galerkin方法求解KdV-B方程

裴凯燕，郭龙飞，任红萍

(太原科技大学应用科学学院，山西 太原 030024)

该问题的解析解为

利用插值型无单元Galerkin方法求解KdV-B方程

裴凯燕，郭龙飞，任红萍

(太原科技大学应用科学学院，山西 太原 030024)

首先讨论移动最小二乘插值法，并利用移动最小二乘插值法建立形函数，结合KdV-B方程的Galerkin积分弱形式，提出求KdV-B方程数值解的插值型无单元Galerkin方法(IEFG)，并推导其相应的公式，跟无单元Galerkin方法相比，利用插值型无单元Galerkin方法计算时，本质边界条件可直接施加，从而可提高计算效率，并给出算例说明了该方法的有效性.

无网格方法;移动最小二乘插值法;形函数;插值型无单元Galerkin方法(IEFG);KdV-B方程

无网格方法是继有限元法之后发展起来的一种新型的数值计算方法，其因为不需要构建网格，只需要节点信息来建立变量的逼近函数，所以具有前期处理简单，计算精度高等优点，目前已经是计算科学的研究热点之一［1-2］.

现有的无单元 Galerkin方法［3］、重构核粒子法［4］、无网格局部 Petrov-Galerkin 方法［5］、配点法［6］、径向基函数法［7］、复变量无网格方法［8］、局部边界积分方程法［9］、边界径向点插值法［10］、边界无单元法［11］等，这些均属于无网格方法.

在构建无网格方法的形函数的过程中，移动最小二乘法是运用最广的方法之一，在它的基础上，Belystschko等人提出了无单元 Galerkin方法(EFG)［3］，Liew等人提出了改进的移动最小二乘法，张赞等人又基于改进的移动最小二乘法，对无单元Galerkin方法进行了改进.

为提高无网格方法的计算速度，Liew、任红萍等人在移动最小二乘近似的基础上，考虑了复变量的情况，建立了复变量移动最小二乘法［12］、复变量移动最小二乘插值法［13］、复变量边界无单元法、复变量无单元Galerkin方法等.

由于通过移动最小二乘法求得的形函数不能够满足Kronecker δ函数的性质，定解问题的边界条件不能够直接施加，计算效率低，故对其进行了改进，即Lancaster提出的移动最小二乘插值法.之后，任红萍等人提出改进的移动最小二乘插值法［14］，并对无单元Galerkin方法作了相应的研究和改进［15］.

KdV-B方程是一类非线性偏微分方程，它是由Burgers方程和Korteweg-de Vries(KdV)方程相结合而成［16］.KdV-B方程来源于很多物理现象，比如潜水波的传播、波在填充有粘性流体的弹性管里的传播和弱非线性等离子波的耗散效应.因此求解KdV-B方程的重要性和实际意义就凸显而出.

1 插值型无单元Galerkin方法形函数的构造方法:移动最小二乘插值法

在移动最小二乘近似中，设被近似函数为u(x)，(x∈D)，且在xi处的值是给出的，记为ui=u(xi)，(i=1，2，…，n).

u(x)的近似函数可以写成如下形式:

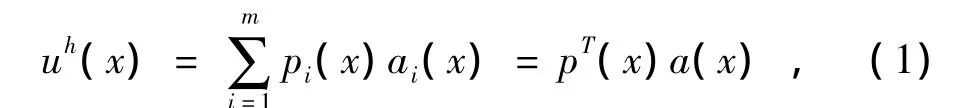
在上式中，pi(x)，i=1，2，…，m，是单项式基函数;ai(x)是对应基函数的系数.

定义如下函数:

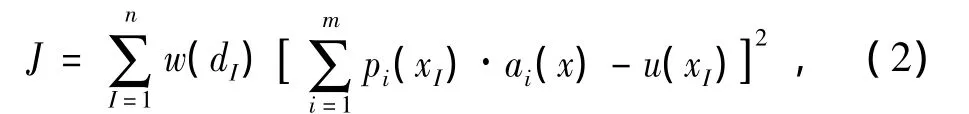
其中，xI，(I=1，2，…，n)，J分别是点x的影响域内的节点和节点误差值的加权平方和，w(dI)是关于x和xI间的距离单调递减的权函数，具有紧支集特性.

式(2)写成矩阵形式为:

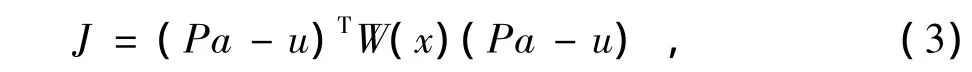
其中

令Ja=0，我们得到

其中矩阵A(x)和B(x)分别为

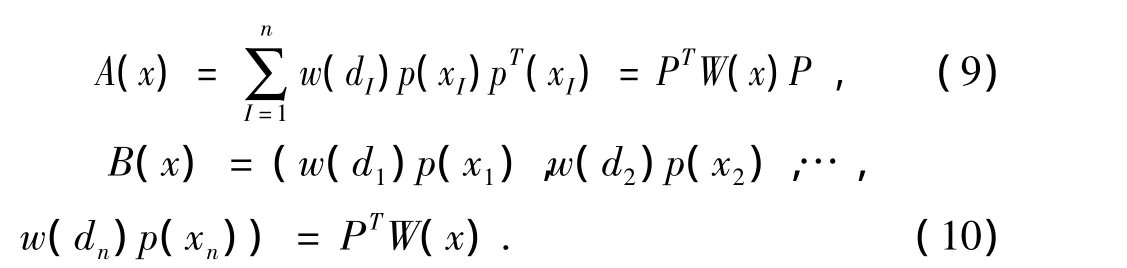
由式(8)可以得到

逼近函数uh(x)的表达式为

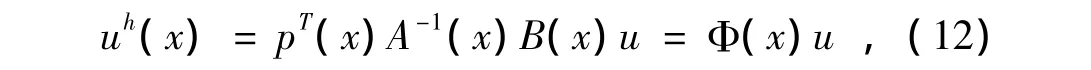
这里Φ(x)称为形函数，

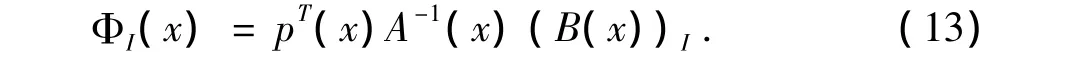
式(12)中的uh(x)不经过插值节点，现在建立插值型移动最小二乘法.

在空间span(p1，p2，…，pm)，我们定义如下内积

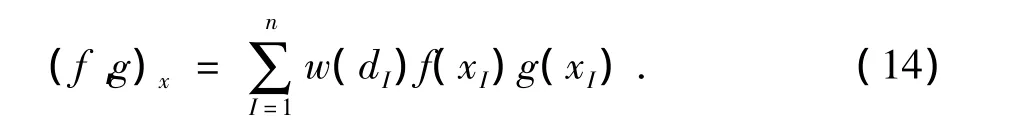
相应定义范数为

在x点基函数p1(x)≡1单位化为

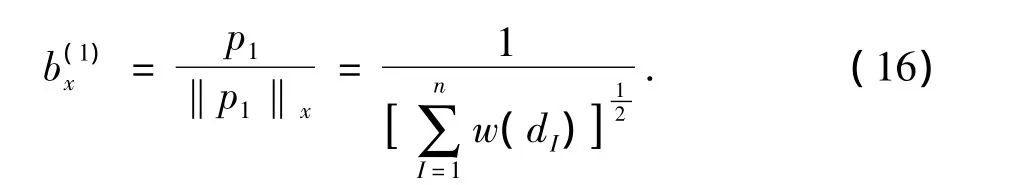
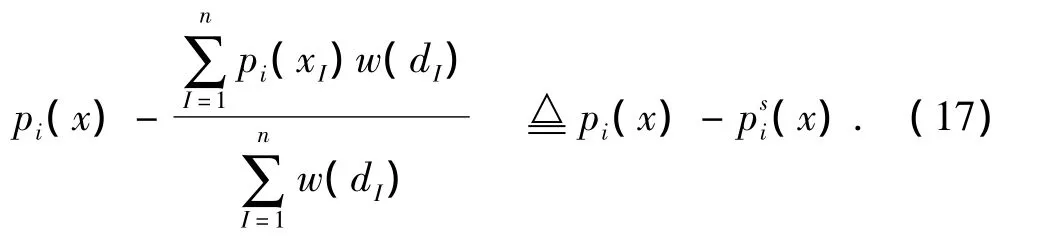
采用新的基函数b(1)x(x)，b(2)x(x)，…，b(m)x(x)和在节点奇异的权函数

其中r是影响域的半径，得到的形函数ΦI(x)，(I=1，2，…，n)，满足 Kronecker δ函数的性质，即

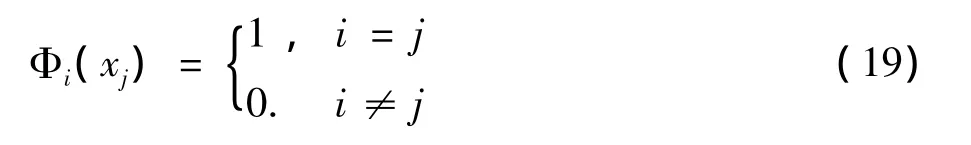
至此我们提出了移动最小二乘插值法，其插值特性在［13］中已经被证明.

2 KdV-B方程的插值型无单元Galerkin方法

KdV-B方程形式如下

其中 ε，λ，γ，和 μ 是参数，角标x和t表示对x，t的微分.

初始条件为

边界条件为

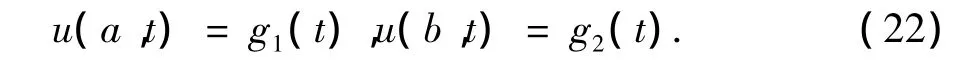
那么式(20)的积分弱形式为

通过分部积分法，我们得到

通过式(12)，得

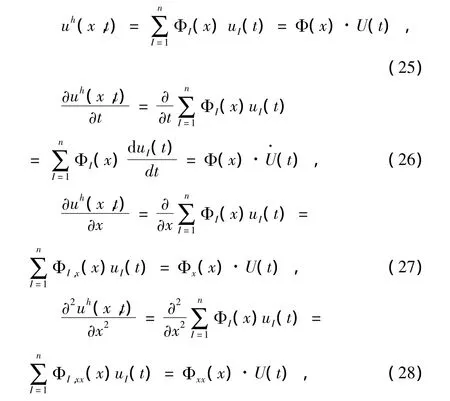
其中

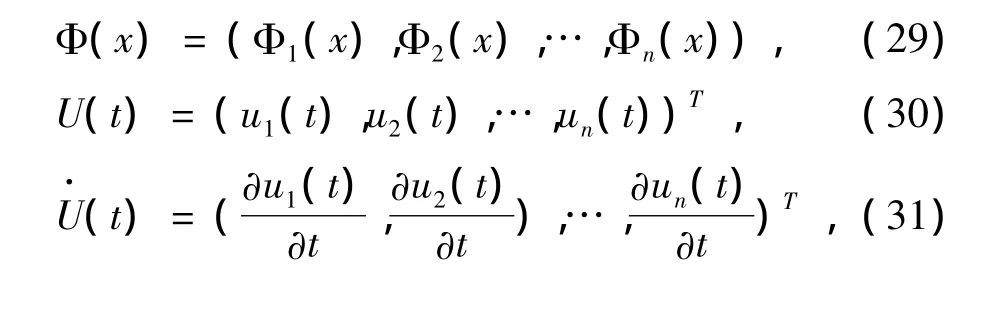
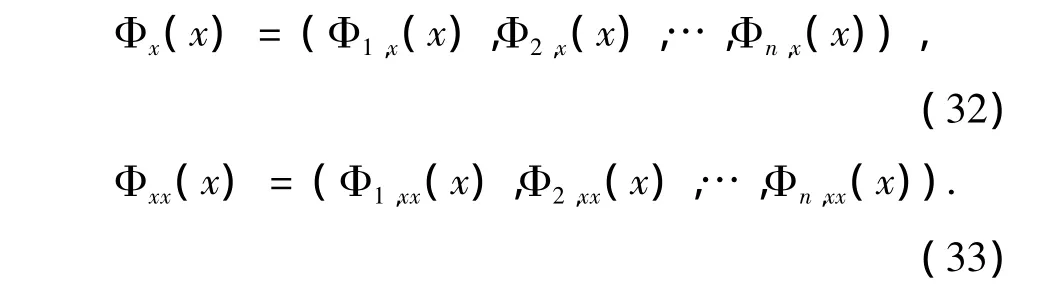
把式(25)-(33)代入式(24)，得

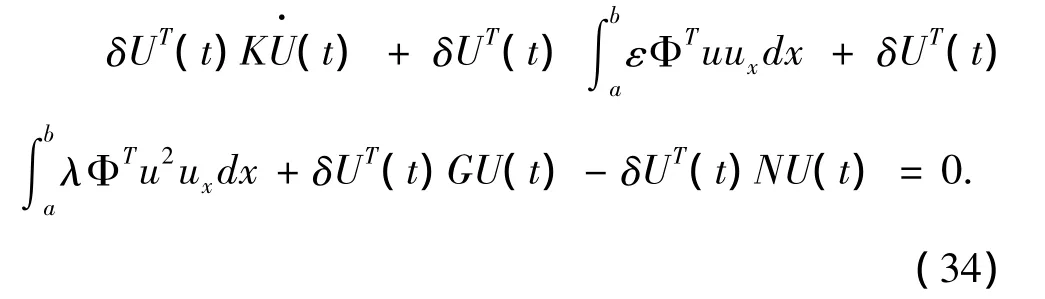
由δUT(t)的任意性，上式可以写成如下形式

其中

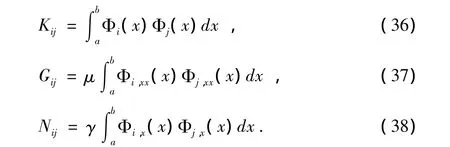
通过中心差分法我们把式(34)中的时间变量离散化，得到

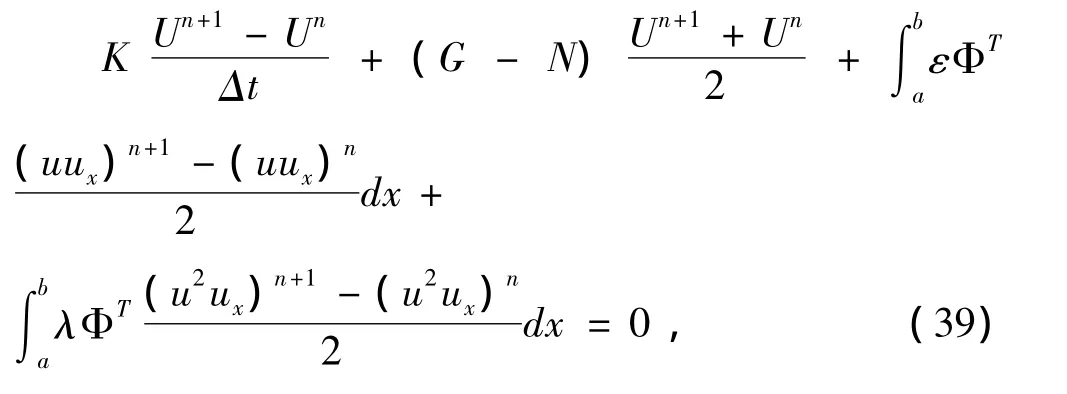
其中，Δt是时间步长，并且

用以下公式就可以把式(39)中的非线性项(uux)n+1和(u2ux)n+1线性化

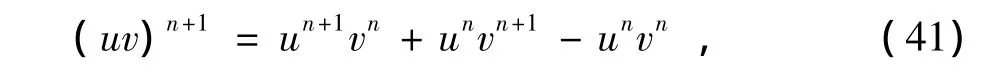
于是，有

因为

我们有

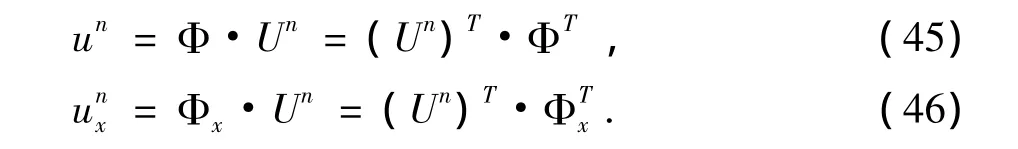
把式(44)-(46)代入式(39)，得

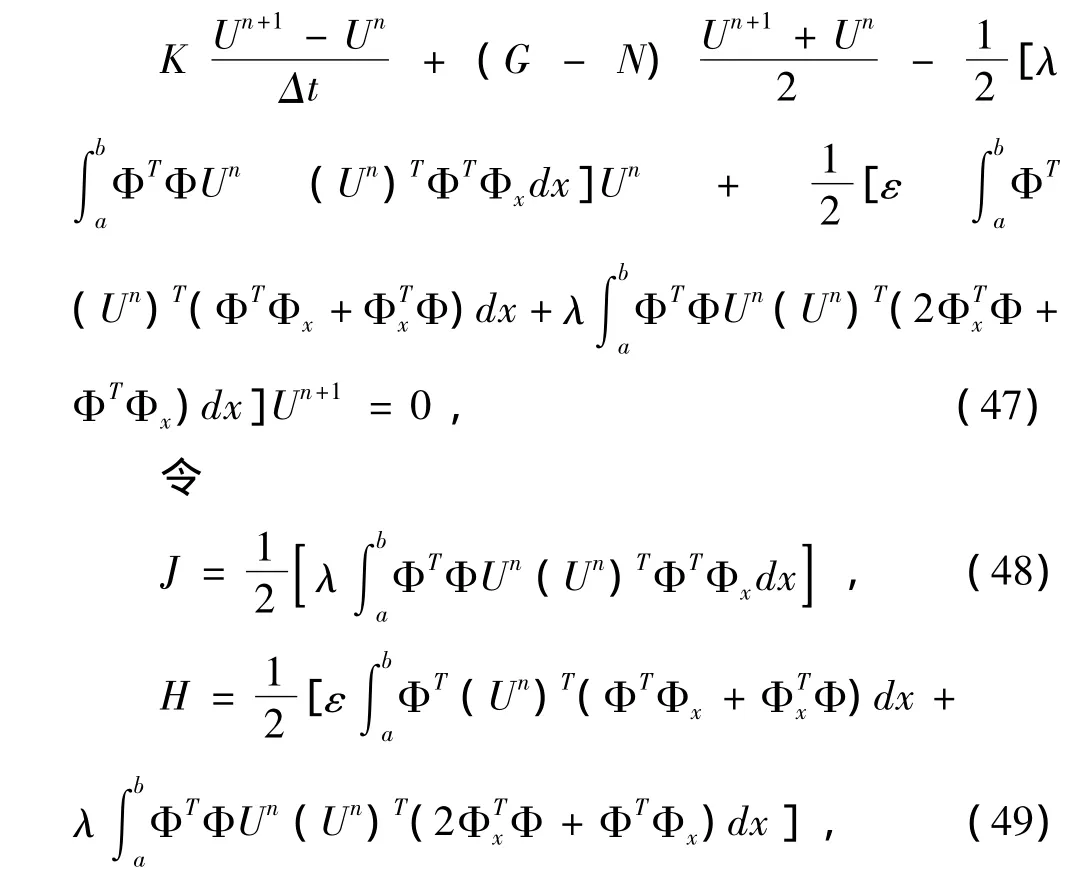
式(47)可以写作

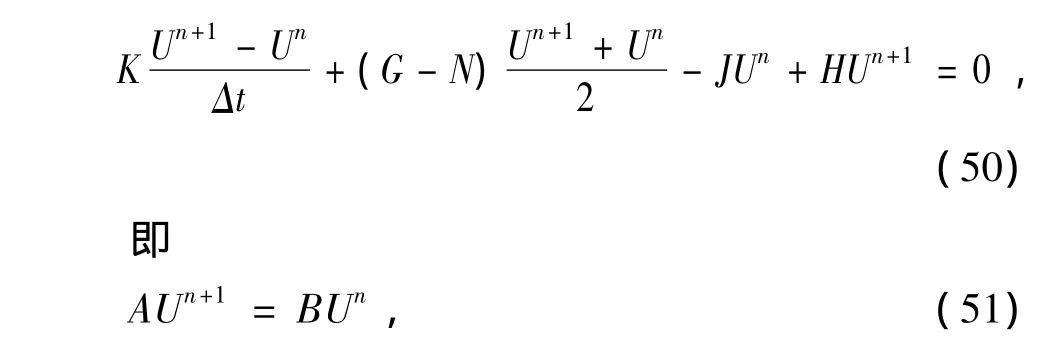
其中

以上过程即为KdV-B方程的插值型无单元Galerkin方法.

3 数值算例

以下给出两个算例来说明插值型无单元Galerkin方法的有效性，并对其数值结果分别与解析解和无单元Galerkin方法的数值解进行了比较.

相对误差公式为

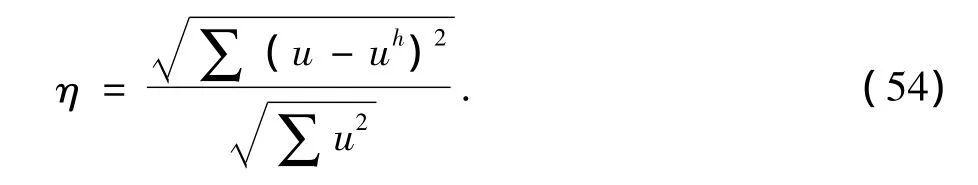
算例中，我们选用了二次基函数 (1，x，x2)和权函数(18).

3.1 算例1

KdV-B方程

边界条件为

初始条件为

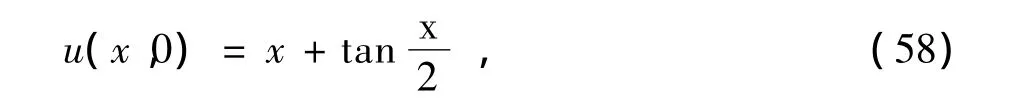
该问题的解析解为

这个算例中，在定义域上均匀分布21个节点，图1为IEFG方法的数值解与解析解在t=0.005时刻的比较，图2为IEFG方法、无单元Galerkin方法的数值解与解析解在t=0.01时刻的比较，可以看到插值型无单元Galerkin方法的数值解与解析解吻合的很好.图3为相对误差和时间步长的关系，时间步长越小相对误差也越小.

3.2 算例2

KdV-B方程

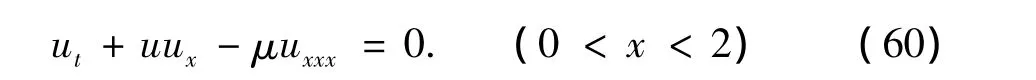
边界条件为

初始条件为

其中

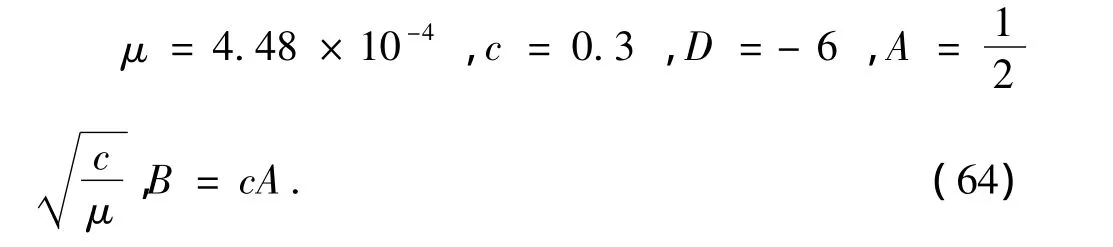
该问题的解析解为

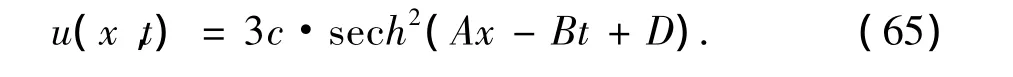
算例中，在定义域上均匀分布81个节点.图4为IEFG方法的数值结果与解析解在t=0.025时刻的对比.图5为IEFG方法、无单元Galerkin方法的数值结果和解析解在t=0.01时刻的比较.图6为相对误差与节点数之间的关系.表1为EFG方法和IEFG方法在t=0.01时刻的相对误差，由表格也可以看出IEFG方法比EFG方法有更高精度.图7为运行时间和迭代次数之间的关系，观察发现插值型无单元Galerkin方法比无单元 Galerkin方法节约了大约30%-50%的计算时间.

4 结论

本文给出了一种由改进的移动最小二乘插值法所得的形函数与KdV-B方程的Galerkin积分弱形式相结合得到KdV-B方程的插值型无单元Galerkin方法，由于移动最小二乘插值法的形函数满足Kronecker δ函数的性质，KdV-B方程的IEFG方法可以直接施加本质边界条件.数值结果表明IEFG方法使得计算精度有所提高，并且计算效率有了明显提高.插值型无单元Galerkin方法比无单元Galerkin方法节约了大约30%-50%的计算时间.

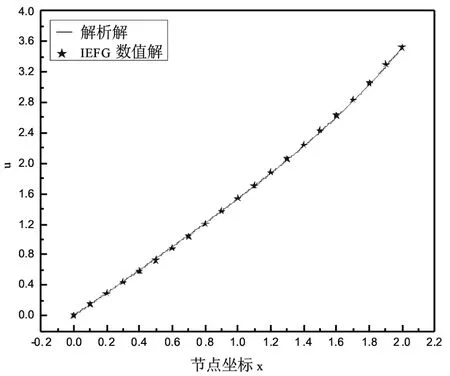
图1.t=0.005时刻的解析解与IEFG数值解Fig.1.Exact solution and numerical results of u(x，0.005)

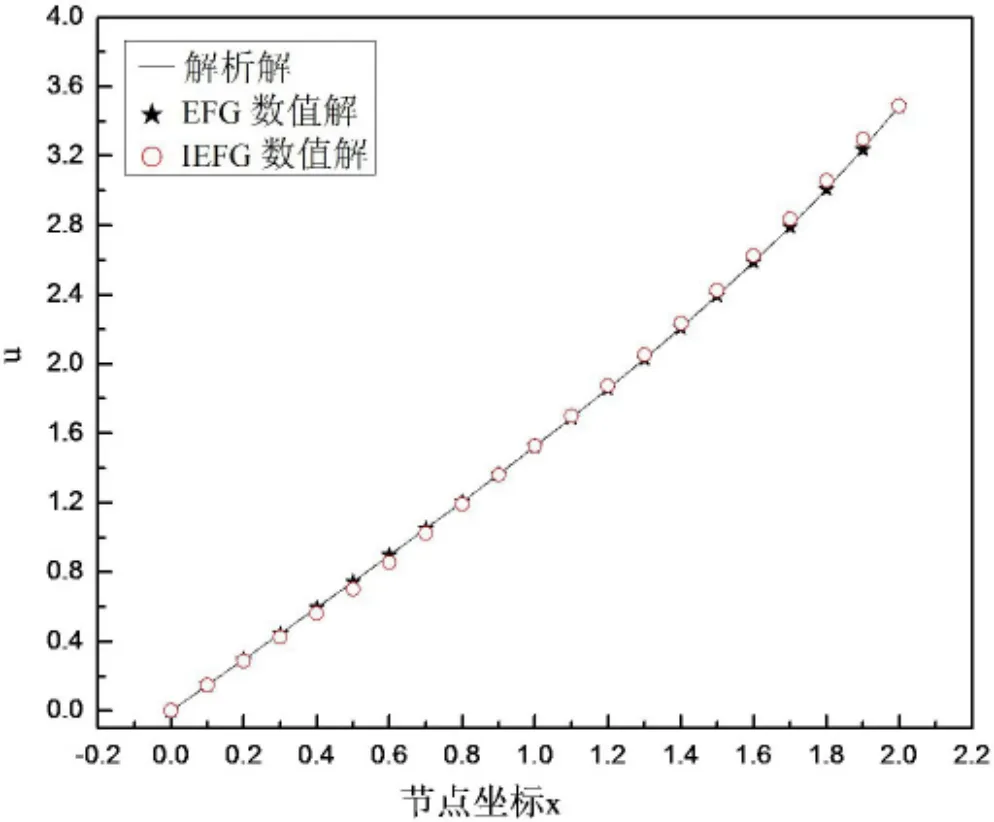
图2 t=0.01时刻的解析解与IEFG、EFG数值解Fig.2 Exact solution and numerical results of u(x，0.01)

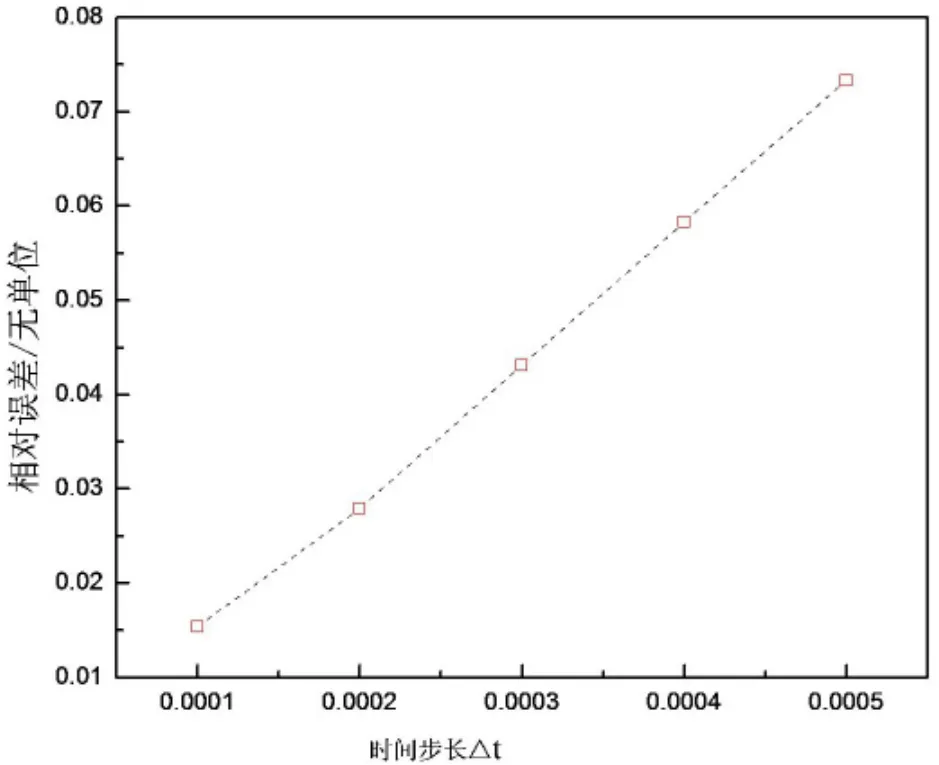
图3 相对误差与时间步长的关系Fig.3 Relationship between the relative error and time step

图4 t=0.025时刻的解析解与IEFG数值解Fig.4 Exact solution and numerical results of u(x，0.025)

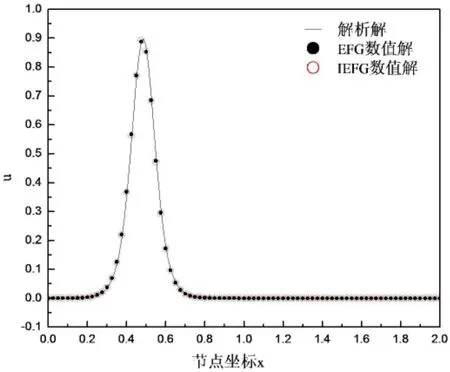
图5 t=0.01时刻的解析解与IEFG、EFG数值解Fig.5 Exact solution and numerical results of u(x，0.01)

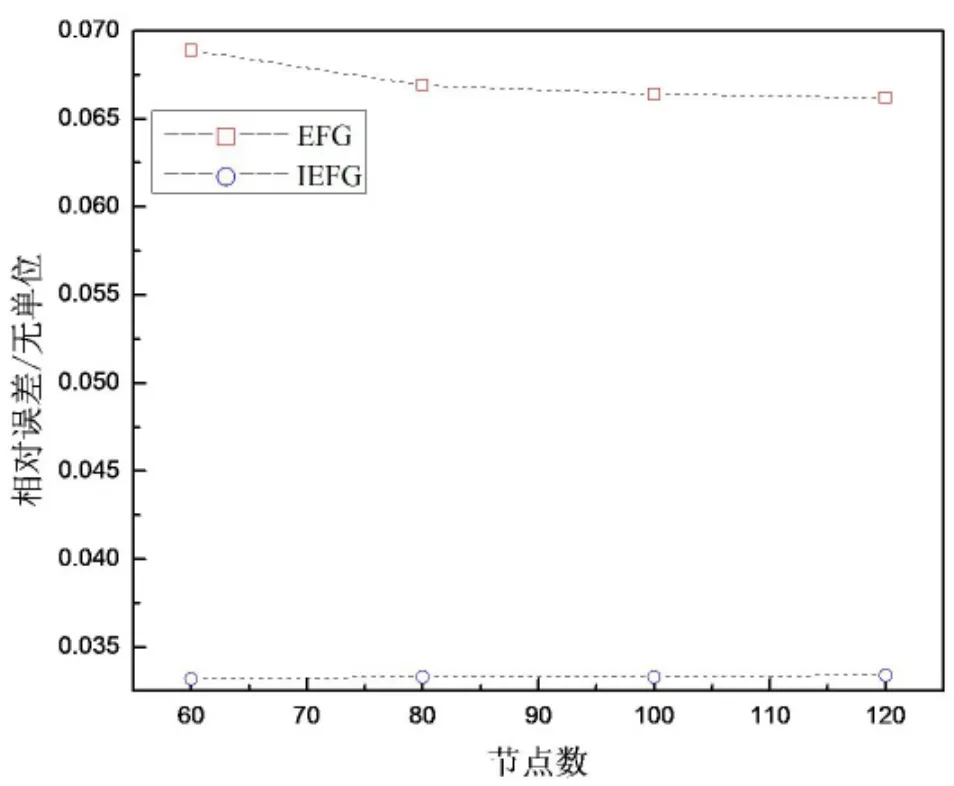
图6 t=0.01时刻的相对误差与节点数的关系Fig.6 Relationship between the relative

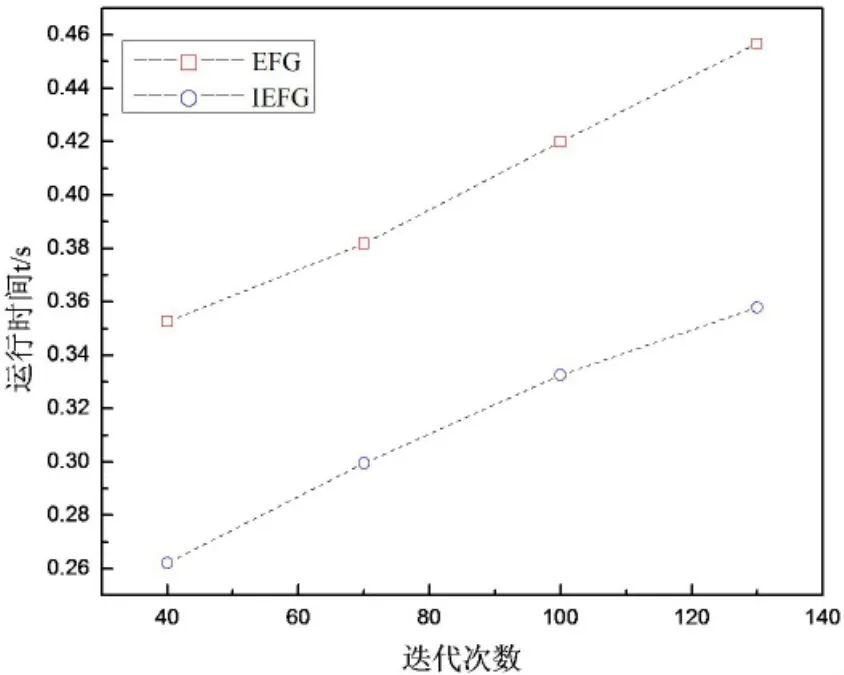
图7 迭代次数和运行时间的关系Fig.7 Relationship between the running time and the number of iterations

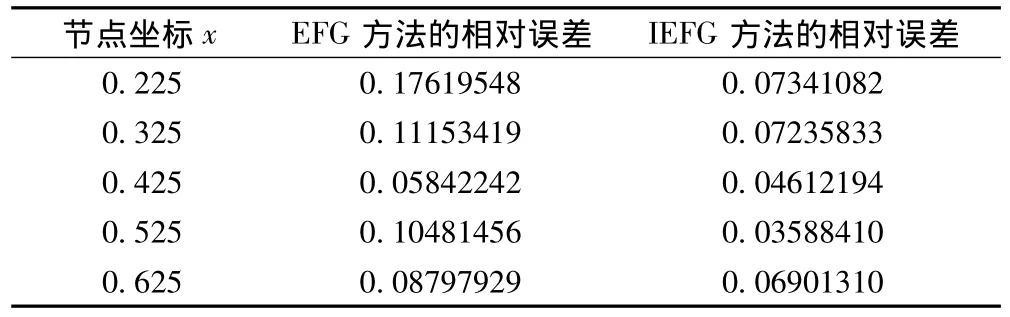
表1 t=0.01时刻的IEFG、EFG方法的相对误差Table 1 The relative error of EFG method and IEFG method at t=0.01

［1］REN HONGPING，CHENG YUMIN.The interpolating element-free Galerkin(IEFG)method for two-dimensional potential problems［J］.Engineering Analysis with Boundary Elements，2012，36(5):873-880.

［2］ZHANG ZAN，WANG JIANFEI，CHENG YUMIN，et al.The improved element-free Galerkin method for three-dimensional transient heat conduction problems［J］.Science China Physics，Mechanics ＆ Astronomy，2013，56(8):1568-1580.

［3］BELYTSCHKO T，LU Y Y，GU L.Element-free Galerkin methods［J］.International Journal for Numerical Methods in Engineering，1994，37:229-256.

［4］LIU W，JUN S，ZHANG Y.Reproducing kernel particle methods［J］.International Journal for Numerical Methods in Engineering，1995，20:1081-1106.

［5］ATLURI S N，ZHU T L.A new meshless local Petrov-Galerkin(MLPG)approach in computational mechanics［J］.Computational Mechanics，1998，22:117-127.

［6］ALURU N R.A point collocation method based on reproducing kernel approximations［J］.International Journal for Numerical Methods in Engineering，2000，47:1083-1121.

［7］WENDLAND H.Meshless Galerkin method using radial basis functions［J］.Mathematics of computation，1999，68(228):1521-1531.

［8］CHENG YUMIN，LI JIUHONG.A complex variable meshless method for fracture problems［J］.Science in China Ser.G Physics，Mechanics＆ Astronomy，2006，49(1):46-59.

［9］ZHU T ，ZHANG J，ATLURI S N.A meshless numerical method based on the local boundary integral equation(LBIE)to solve linear and non-linear boundary value problems［J］.Engineering Analysis with Boundary Elements，1999，23:375-389.

［10］GU Y T，LIU G R.A boundary radial point interpolation method(BRPIM)for 2-D structural analyses［J］.Structural Engineering and Mechanics，2003，15:535-550.

［11］CHENG YUMIN，PENG MIAOJUAN.Boundary element-free method for elastodynamics［J］.Science in China Ser.G Physics，Mechanics ＆Astronomy，2005，48(6):641-657.

［12］LIEW K M，FENG C，CHENG YUMIN，et al.Complex variable moving least-squares method:A meshless approximation technique［J］.International Journal of Numerical Methods in Engineering，2007，70:46-70.

［13］REN HONGPING，CHENG JING，HUANG AIXIANG.The complex variable interpolating moving least-squares methed［J］.Applied Mathematics and Computation，2012，219:1724-1736.

［14］REN HONGPING，PEI KAIYAN，WANG LIPING.Error analysis formoving least squares approximation in 2D space［J］.Applied Mathematics and Computation，2014，238:527-546.

［15］REN HONGPING，WANG LIPING，ZHAO NA.The interpolating element-free Galerkin(IEFG)method for steady-state heat conduction problems［J］.International Journal of Applied Mechanics，2014，6(3):1450024.

［16］CHENG RONGJUN，CHENG YUMIN.A meshless method for the compound KdV-Burgers eqution［J］.Chinese Physics B，2011，20(7):070206.

Interpolating element-free Galerkin method for the compound KdV-B equation

PEI Kai-yan，GUO Long-fei，REN Hong-ping
(School of Applied Science，Taiyuan University of Science and Technology，Taiyuan 030024，P.R.C.)

An interpolating moving least squares method is discussed first.Combining the shape function constructed by the IMLS method and Galerkin weak form for the compound KdV-B equation，the interpolating element-free Galerkin(IEFG)method for the compound KdV-B equation is put forward，and the corresponding formulae are obtained.Compared with the conventional EFG method，in the IEFG method，the boundary conditions can be directly applied.Numerical results show that it not only has high computational accuracy，but also enhances computational efficiency greatly.

meshless method;interpolating moving least squares method;shape function;interpolating element-free Galerkin(IEFG)method;KdV-B equation

O24

A

2095-4271(2015)06-0748-06

10.11920/xnmdzk.2015.06.018

2015-03-15

裴凯燕(1990-)，女，汉族，山西人，硕士研究生，研究方向:微分方程与工程数值计算

任红萍(1966-)，女，汉族，山西人，教授，博士，研究方向:工程数值计算.E-mail:hpren@tyust.edu.cn

山西省自然科学基金项目(2014011006-2);太原科技大学博士研究基金项目(No.20102024);太原科技大学研究生科技创新项目(No.20145010)

(责任编辑:付强，张阳，李建忠，罗敏;英文编辑:周序林)