中立型分数阶微分控制系统能控性*

王智，蒋威(安徽大学数学科学学院，安徽合肥230601)

中立型分数阶微分控制系统能控性*

王智，蒋威
(安徽大学数学科学学院，安徽合肥230601)

摘要:研究一类分数阶中立型微分控制系统的能控性问题，对系统状态方程的分析，利用拉普拉斯变换通过基本控制系统的基础解给出了控制系统通解的表达式，并且通过构造格拉姆矩阵，研究了控制系统能控性的充分必要条件;最后通过举出一个格拉姆矩阵的计算举例来进行验证。

关键词:分数阶;微分方程;能控性;中立型

在科学生产等与人类有关的发展过程中，系统的能控性在每次的进步中发挥着重要的作用，诸如管理系统、生态系统、电力系统、工业工程系统等实际控制系统的研究，出现了大量的控制微分问题，引起不少学者的关注，并取得了重要的成果［1－3］。文献［4］中，研究了分数阶微分控制系统能控性。在文献［5］的基础上，进一步研究中立型分数阶微分控制系统能控性。

研究如下形式的中立型分数阶微分控制问题的能控性:

其中x(t)∈Rn为状态变量，CDα(·)定义为α阶的Caputo导算子(0＜α＜1)，常数矩阵C满足C∈Rn×p，矩阵A，B，D是n阶常数矩阵且D≠0，初始函数φ∈C(［－1，0］，Rn)控制输入u(t)∈Rp。

1　预备知识

定义1［6］设f(t)∈C(［0，∞)，R)，称

为α阶Riemann-Liouville分数积分。

定义2［6］设f(t)∈C(［0，∞)，R)，α∈(0，1 )称

为f(t)的α阶Caputo分数导数。

定义3［6］具有双参数的Mittag-Leffler函数为

2　基本系统与概念

定义4如果存在函数X(t)满足:

这里，I为n×n单位矩阵，则称X(t)为系统(1)的基础解。

对式(1)的基础解X(t)，设Xk(h) = X(k+h)，h∈［0，1］，k = 0，1，2，…，那么对于t∈［k，k+1］，X(t) = Xk(t－k)，根据式(2)，可得:

且Ik=［0，0，…，I］n×n(k+1)，即得:

定理1方程(2)的解表示为

证明利用拉普拉斯变换，可以得:

X(t) = Xk(t－k)，即证得:，定理证毕。

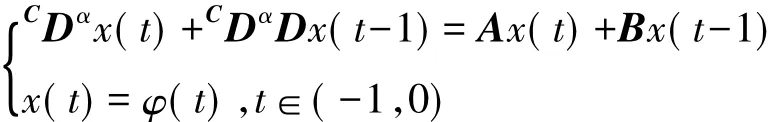
定理2系统(1)的解为

3　主要结果

构造格拉姆矩阵W(0，t)满足:

这里“T”表示矩阵的转置。

定理3式(1)在区间［0，t1］上可控的充分必要条件矩阵W(0，t1)正定。

证明先证式(1)能控。

因为W(0，t1)是正定的，也就是说W(0，t1)是非奇异的，知W(0，t1)的逆存在，定义控制u(t)满足:

为方便讨论，这里记:x(t1) = b(b为任意实数)，函数G(t)满足:

将式(7)代入式(6)，根据式(5)，可得:即系统(1)是能控得证。

另一方面，如果W(0，t1)不是正定的，即W(0，t1)是奇异的。设存在非零矩阵Z，使得ZTW(0，t1) Z = 0，且:

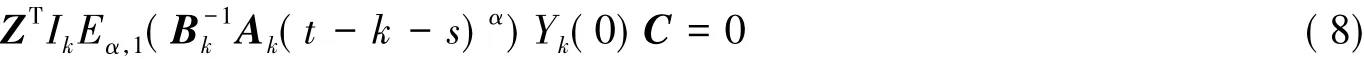
假定系统是能控的，那么一定存在控制u1(t)，使得在终点状态x(t1) = 0，且对应的控制u1(t)

同理，矩阵Z也有一个相对应的控制u2(t)，且满足:

比较式(9)、(10)，化简可得:

将其两边同时乘以ZT，有:

比较式(7)，知ZTZ=0，而这与已知矛盾，即证明完毕。

4　应用实例

考虑式(1)，选择t1=1，k=0，α=β=，有Ak=A0=，Bk=Ik=I，C=，Y(0) = X(0) = I，应用定00理4.1，证明式(1)是能控的。因为:

通过计算，得到:

参考文献:

［1］郑祖庥.泛函微分方程理论［M］.合肥:安徽教育出版社，1994

［2］刘豹，唐万生.现代控制理论［M］.3版.北京:机械工业出版社，2006

［3］蒋威.退化时滞微分系统［M］.合肥:安徽大学出版社，1998

［4］JIANG W.The Controllability of Fractional Control Systems with Control Delay［J］.Computers and Mathematics with Applications，2012，64(10):3153-3159

［5］蒋威.中立型线性控制系统的能控性［J］.中国控制，1995(2):121-128

［6］PODLUBNY I.Fractional Differential Equations［M］.San Diego Academic Press，1999

［7］ZHOU X F，WEI J，HU L G.Controllability of a Fractional Linear Time-invariant Neutral Dynamical System［J］.Appl Math Lett，2013(26):418-424

［8］FU X.Controllability of Neutral Functional Differential Systems in Abstract Space［J］.Appl Math Comput，2003(141):281-296

［9］LAKSHMIKANTHAM V.Theorem of Fractional Functional Differential Equations［J］.Nonlinear Anal，2008，69(10):3337-3343

［10］WEI J，SONG WZ，FEI S.The Function-controllability of the Nonlinear Control Systems with State and Control Delay［J］.Word Scientific London，2000(10):143-148

Controllability of Neutral Fractional Differential Control Systems

WANG Zhi，JIANG Wei
(School of Mathematical Sciences，Anhui University，Anhui 230601，China)

Abstract:A class of the controllability of neutral fractional differential control systems is studied，and the systems equation is analyzed.By using of Laplace transformation for the basic control system，the control systems solution expression is given，and by Gram-matrix construction，the necessary and sufficient conditions for controllability of the control system is researched.Finally the validity of the theory is verified by example.

Key words:fractional; differential equations; controllability; neutral

中图分类号:O172

文献标识码:A

文章编号:1672－058X(2015) 08－0001－05

doi:10.16055/j.issn.1672－058X.2015.0008.001

收稿日期:2015－01－03;修回日期:2015－02－28.

*基金项目:国家自然科学基金(11371027).

作者简介:王智(1988-)，男，安徽淮南人，硕士硕士生，从事微分控制系统能控性研究.