最优正规基下并行乘法器的设计*

苏丹丹，付　萍(.罗定职业技术学院，广东罗定5700; .北京昌平区回龙观中学，北京000)

最优正规基下并行乘法器的设计*

苏丹丹1，付萍2
(1.罗定职业技术学院，广东罗定527200; 2.北京昌平区回龙观中学，北京102200)

摘要:利用简单的组合逻辑电路分别在Ⅰ型和Ⅱ型最优正规基上设计出了新的并行乘法器，其中Ⅰ型最优正规基并行乘法器所需异或门数为3n－4，与门数为n，Ⅱ型最优正规基并行乘法器所需异或门数为2n－2，与门数为n;与Sunar和Koc于2001年在Ⅱ型最优正规基上提出的并行正规基乘法器对照，此乘法器大大减少了所需要的门数，从而有效地降低了硬件消耗的资源.

关键词:有限域;最优正规基;乘法器;门数

有限域计算(即加法，减法，乘法和求逆等)被广泛用于编码理论，计算机代数学和密码学［1，2］.有限域计算尤其乘法计算极大地影响着各种密码算法的加/解密速度，因此，设计性能优越的乘法器显得尤其重要.各种乘法器的算法极大地依赖于有限域基的选择.有限域有多种基，如多项式基、正规基等.在这些基中，使用正规基对算术操作的硬件执行是非常有效的.1986年，Omura和Massey首次在文献［3］中提出正规基乘法器.

根据Menezes在文献［1］中所列举的数据，在n∈[2，2 001 ]范围内属于Ⅰ型最优正规基的m有117个，属于Ⅱ型最优正规基的m有319个.因此，研究最优正规基是非常有意义的.尽管Massey-Omura正规基乘法器对Ⅰ型和Ⅱ型最优正规基都有效，但所需异或门数为2n(n－1).基于Massey-Omura乘法器，2001年，Sunar 和Koc在文献［4］中在Ⅱ型最优正规基上提出了一种并行正规基乘法器，其所需异或门数为1.5n(n－1)，与门数为n2.文中利用简单的组合逻辑电路分别在Ⅰ型和Ⅱ型最优正规基上设计出新的并行乘法器，其中Ⅰ型最优正规基并行乘法器所需异或门数为3n－4，与门数为n，Ⅱ型最优正规基并行乘法器所需异或门数为2n－2，与门数为n.与Sunar-Koc正规基乘法器对照，此乘法器大大减少了所需要的门数，从而有效地降低了硬件消耗的资源.

1　相关引理和定理

引理1［5］设和为E在F上互为对偶的两组基，则对

任意u∈E，有

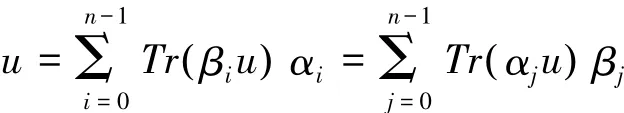
引理2［6］设为E在F上的一组Ⅰ型最优正规基，T=(ti，j)为其乘法表。则当

j=0，1，…，n－1时，有

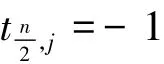
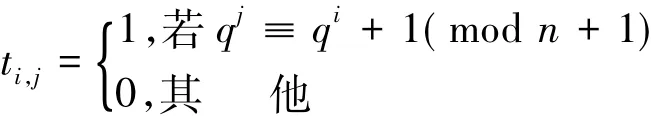
引理3［7］设为E在F上的一组Ⅰ型最优正规基，则N的对偶基为

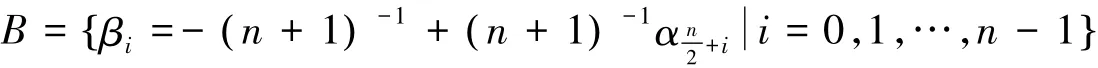
定理1［8］设n+1是素数，q是模n+1的一个原根，则F上n个非单位元的n+1次单位根是线性无关的，且组成E在F上一组最优正规基，记为，这里α是一个n+1次本原单位根，称N为E在F上的一组Ⅰ型最优正规基。

引理4［6］设为F2n在F2上的一组Ⅱ型最优正规基，T=(ti，j)为其乘法表，则

而当i=1，2，…，n－2时，有

引理5［9］设为F2n在F2上的一组Ⅱ型最优正规基，则N是自对偶正规基。

2　算法设计

设X，Y∈F2n，元素X和Y分别用最优正规基N及其对偶基B表示为

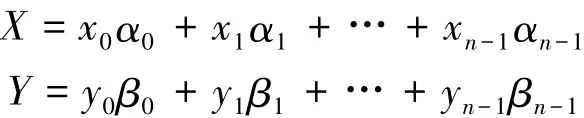
设二者的乘积用对偶基表示为

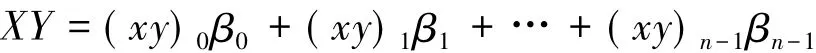
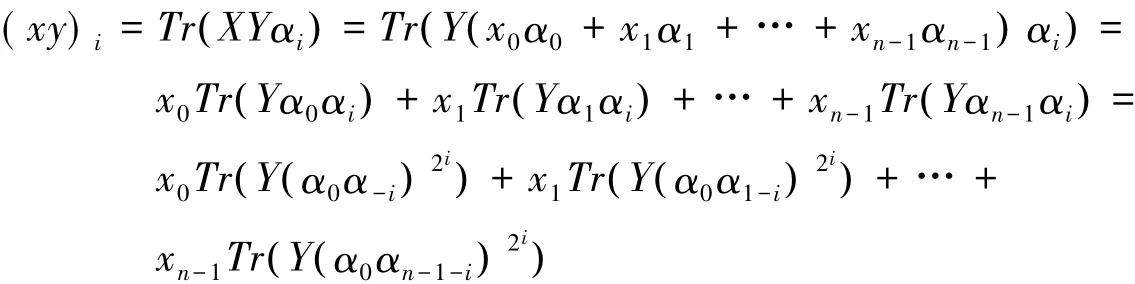
(其中足标均取模n的最小非负剩余).

又由引理1知:

同理有:

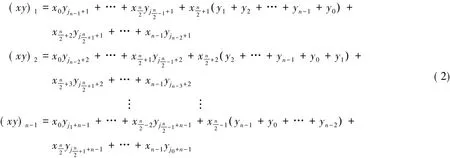
其中足标均取模n的最小非负剩余.

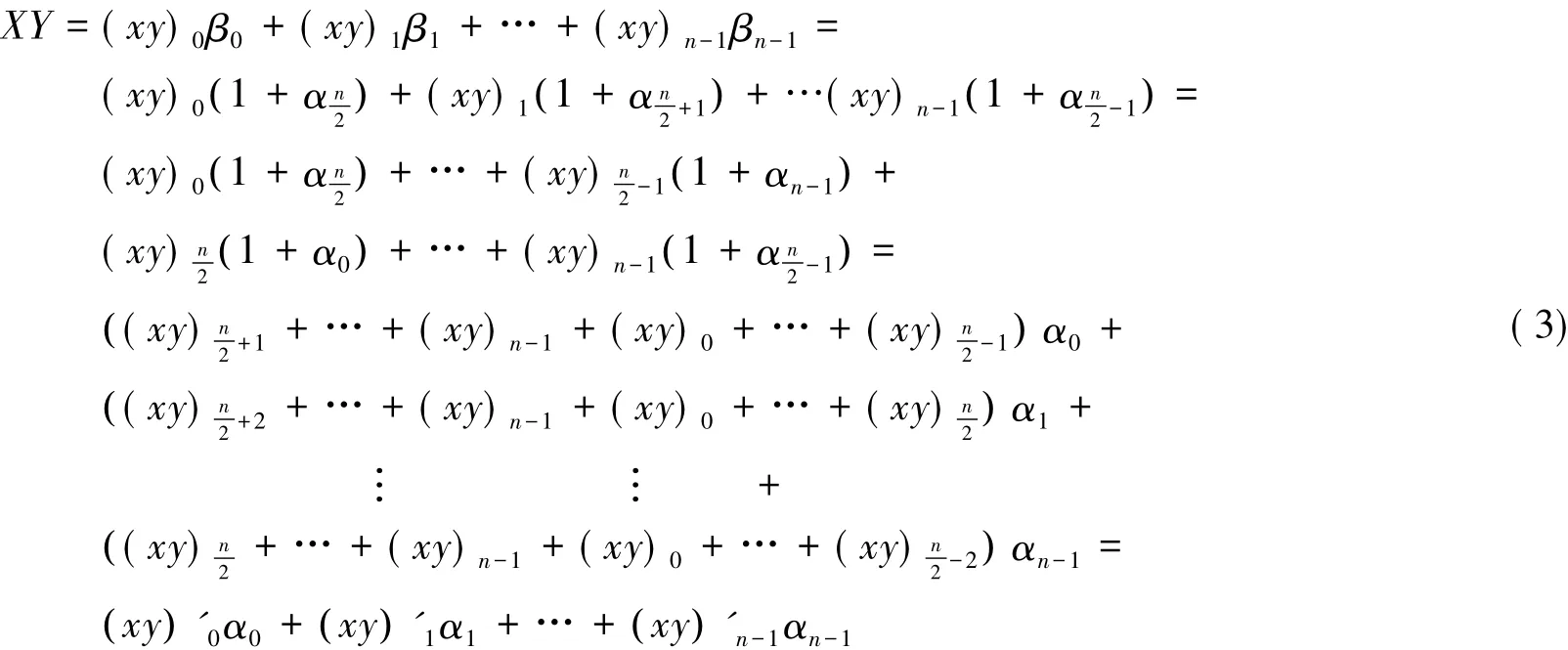
其中足标均取模n的最小非负剩余.

情形2:若N为Ⅱ型最优正规基，则由引理4知αα0=α1，ααn－1=αn－1+αt，其中t=0，1，…，n－1且2t+1≡±3 (mod 2n+1).以及i=1，2，…，n－2，有ααi=αm+αk，其中m，k = 0，1，…，n－1，2m≡2i+1(mod 2n+1)，2k≡－(2i+1)(mod 2n+1)，故

又由引理1知:

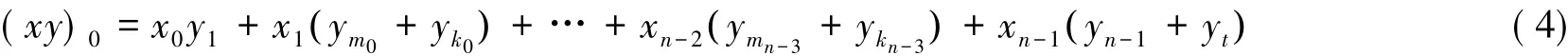
类似地可得:

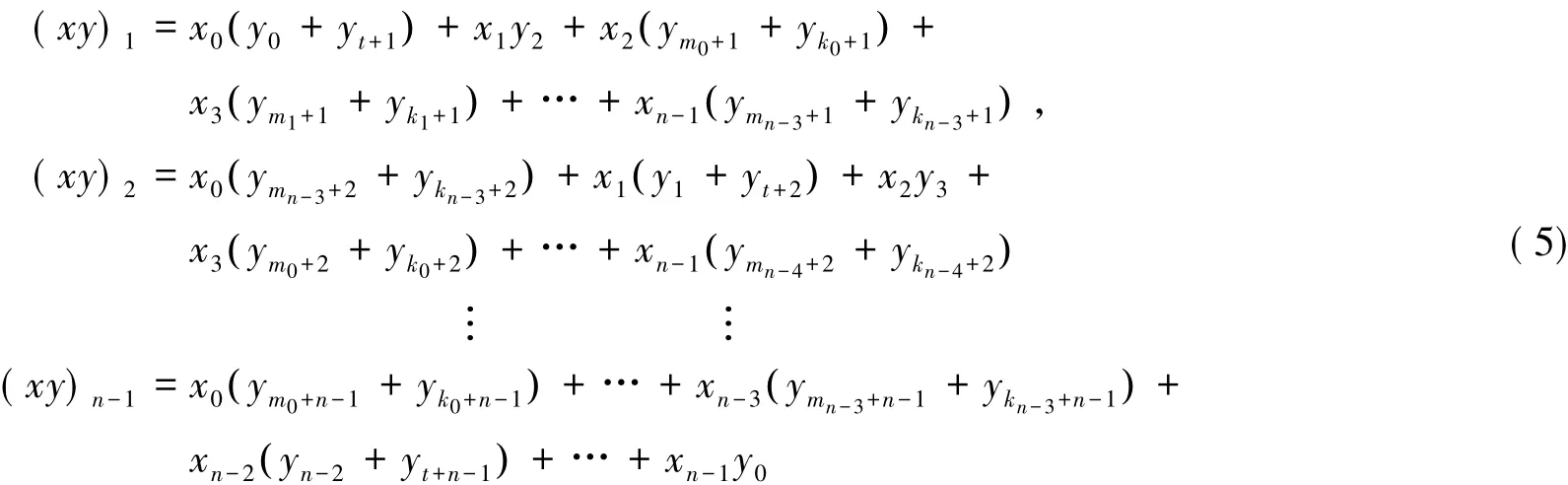
其中足标均取模n的最小非负剩余.

进而由引理5可知N是自对偶的，故

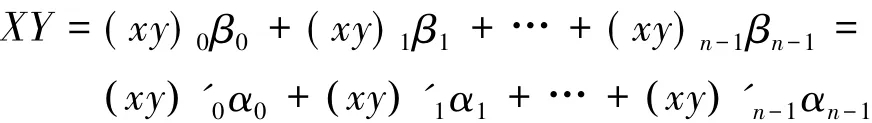
综上所述，完成一次乘法计算需要3步:

(Ⅰ)确定yj0，yj1，…，yjn－1，yjn+1，…，yjn－1及yt，ym0，ym1，…，ymn－3，yk0，从而获得所需的yi，i=0，1，…，n－1.

22

(Ⅱ)利用(1)，(2)，(3)，(4)式计算(xy)0，(xy)1，…，(xy)n－1.

(Ⅲ)若N为Ⅰ型最优正规基，利用(3)式把XY在对偶基B上转换到最优正规基N上表示.

第一步可借助计算机工具(使用C/C++/Matlab程序)确定，第二、三步由简单的组合逻辑电路实现.第一步简单的Matlab程序如下:

输出结果为

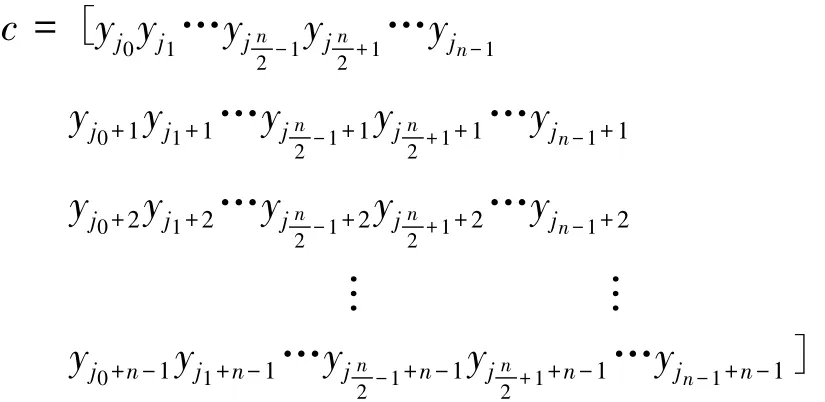
确定yt，ym0，ym1，…，ymn－3，yk0，yk1，…，ykn－3程序类似.

3　算法复杂度的简单分析

若N为Ⅰ型最优正规基，在计算(xy)i，i=0，1，…，n－1时，所需的异或门数为2n－2，与门数为n;在计算(xy ) 'i，i=0，1，…，n－1时，所需的异或门数为n－2.综合所需的异或门数为3n－4，与门数为n.若N为Ⅱ型最优正规基，在计算(xy)i=(xy ) 'i，i=0，1，…，n－1时，所需的异或门数为2n－2，与门数为n.

设计将复杂和消耗资源的工作由计算机工具处理(使用C/C++/Matlab程序)，而实际设计的硬件电路最后形式是简单的组合逻辑电路，且该最优正规基下的并行乘法器，Ⅰ型最优正规基并行乘法器所需异或门数为3n－4，与门数为n，Ⅱ型最优正规基并行乘法器所需异或门数为2n－2，与门数为n.

参考文献:

［1］MENEZES A J.Applications of Finite Fields［M］.Boston:Kluwer Academic，1993

［2］LIDL R，NIEDERREITER H.Introduction to Finite Fields and Their Applications［M］.New York:Cambridge University Press，1994

［3］OMURA J，MASSEY J.Computational Method and Apparatus for Finite Field Arithmetic.US Patent Number 4587627［P］.1986

［4］SUNAR B，KOC C K.An Efficient Optimal Normal Basis TypeⅡmultiplier［J］.IEEE Trans on Computer，2001，50(5):83-87

［5］GEISELLMANN W，GOLLMANN D.Duality and Normal Basis Multiplication［J］.Cryptography and CodingⅢ，1991(187):195

［6］廖群英，孙琦.有限域上最优正规基的乘法表［J］.数学学报，2005，48(5):947-954

［7］WAN Z X，ZHOU K.On the Complexity of the Dual Basis of a TypeⅠOptimal Normal Basis［J］.Finite Fields and Their Applications，2007，13:411-417

［8］MULLIN R，ONYSZCHUK I，VANSTONE S，et al.Optimal Normal Bases in GF(pn)［J］.Discrete Applied Math，1988-1989，22:149-161

［9］LIAO Q Y，SUN Q.Normal Bases and Their Dual-bases Over Finite Fields［J］.Acta Mathematica Sinica，English Series，2006，22 (3):845-848

Parallel Multiplier Design based on optimal Normal Basis

SU Dan-dan，FU Ping
(1.Luoding Polytechnic，Luoding 527200，China; 2.Beijing Changping Huilongguan School，Beijing 102200，China)

Abstract:A new parallel multiplier is designed by simple combinational logic circuits based on type I optimal normal basis and typeⅡoptimal normal basis respectively.For the type I optimal normal basis，the parallel multiplier needs 3n-4 XOR gates and n AND gates，for the typeⅡoptimal normal basis，the parallel multiplier needs 2n-2 XOR gates and n AND gates.Compared with the normal basis parallel multiplier based on typeⅡoptimal normal basis proposed by Sunar and Koc in 2001，this multiplier greatly reduces required gates so as to effectively decrease the resources of consumption.

Key words:finite fields; optimal normal basis; multipliers; gates

中图分类号:O154.2

文献标识码:A

文章编号:1672－058X(2015) 08－0014－05

doi:10.16055/j.issn.1672－058X.2015.0008.004

收稿日期:2015－05－08;修回日期:2015－06－20.

*基金项目:国家自然科学基金资助项目(10990011).

作者简介:苏丹丹(1980-)，女，湖北随州人，讲师，硕士研究生，从事应用数论研究.