多变时滞不确定中立型系统的滑模控制*

董翠丽，蒋　威(安徽大学数学科学学院，合肥230601)

多变时滞不确定中立型系统的滑模控制*

董翠丽，蒋威
(安徽大学数学科学学院，合肥230601)

摘要:研究了不确定中立型系统的滑动模态控制.系统含有多个变时滞和非线性外部干扰项;根据当前状态和时滞状态给出了滑模面的设计，滑模控制器的设计保证了系统的状态轨线在有限时间内被驱动到指定的滑模面上并保持运动;再利用构造Lyapunov函数的方法给出了闭环系统渐进稳定的一个充分条件，充分条件以线性矩阵不等式的形式给出.

关键词:变时滞中立型系统;滑模控制器;线性矩阵不等式

滑模变结构控制，简称滑模控制.其主要研究的是一类非线性控制理论，是由Utkin等人提出并倡导的［1］.经历近几十年的研究，已在各个领域得到了迅速发展及广泛的应用.并形成了一个相对独立的研究分支.在变结构控制系统中，其非线性主要是体现在控制作用的不连续特性上.可以将系统的运动分成两个阶段:第一阶段是到达运动阶段，即通过滑模控制器的设计保证系统运动在有限时间内到达预先设定好的滑模面上;第二阶段是设计一种稳定的滑模面，并在滑模控制器的作用下保证系统的滑模运动是渐进稳定的.滑模变结构控制的优点在于:当系统进入滑模运动阶段，系统具有对参数摄动和外界干扰及不确定性的不敏感性.这种不敏感性表明，滑模控制非常适合作为一种不确定性系统的鲁棒控制器.目前，变结构控制理论已经受到了国内外学者的广泛重视［2，3］.

在实际控制系统中，大多数系统普遍存在不确定因素、状态时滞及控制变量时滞，且匹配条件往往不容易得到满足，这就使得滑模控制系统很难达到所期望的良好品质.为此，针对不同类型的实际系统的滑模控制问题进行了广泛而深入的研究［4－7］.将研究具有多个变时滞且含有多个非匹配不确定项和非线性外部干扰项的中立型系统的滑动模态控制.

1　预备知识

考虑具有非线性干扰和多变时滞的不确定中立型系统:

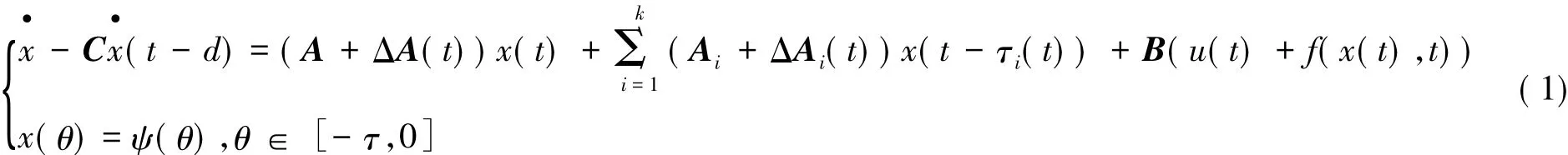
其中x(t)∈Rn，u(t)∈Rm分别为系统的状态变量和控制输入，f(x(t)，t)∈Rn为系统的外部干扰项，ψ(θ)为状态初始条件，A、B、C和Ci，(i=1，…，k)为具有相容维数的实常数矩阵，ΔA(t)和ΔAi(t)，(i= 1，…，k)表示时变参数不确定性，0＜d＜τ为已知的实常数时滞，τi(t)，(i = 1，…，k)为时变时滞且满足0≤τi(t)≤τ，(t)≤1－ε，(i=1，2，…，k)其中0＜ε＜1为常数.

对于式(1)给出假设条件:

(a)假设矩阵B是列满秩的，并且(A，B)是可镇定的，即存在一个实矩K∈Rm×n使得A－BK是稳定的.

(b)ΔA(t) = DF(t) E，ΔAi(t) = DiFi(t) Ei，i=1，2，…，k，其中:D，E，Di和Ei，(i=1，2，…，k)是已知的常数矩阵，F(t)和Fi(t)是未知的时变实矩阵且满足.

(c)外部干扰项f(x(t)，t)∈Rn是有界的，即f(x(t)，t)≤ρ，其中ρ＞0是已知常数.引理1［7，8］设X，Y是适合维数的实数矩阵，则对于任意常数μ＞0，有:

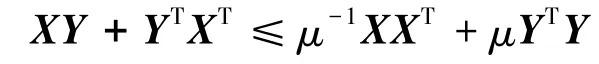
引理2［7，8］设D和E是适合维数的实数矩阵，F(t)是适合维数的时变实矩阵且满足:

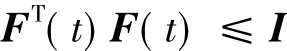
则对于任意常数μ＞0，有:DF(t) E+ETFT(t) DT≤μ－1DDT+μETE.

主要目标是设计一个滑模控制器，使得式(1)的状态轨线在有限时间内达到所期望的滑模面上，并保证闭环系统是渐进稳定的.

根据式(1)的当前状态和时滞状态，设计一个滑模面:

其中P是待选的正定矩阵.

2　滑模控制器的设计

滑模控制器的设计需要两步来完成.第一步骤:设计一个滑模控制器，并保证式(1)的状态轨线在有限时间内达到滑模面式(3)上且在其上进行运动.第二步骤:设计一种稳定的滑模面，并保证系统在该滑模面上的运动是渐进稳定的.

考虑式(1)的控制输入:

其中K为m×n阶实矩阵且满足A－BK是稳定的，

其中uα，uβ分别是系统(1)的等价控制和开关控制，ε0是一个正常数.sign(s(t) )为符号函数，即:sign(s(t) ) =［sign(s1(t) )，sign(s2(t) )，…，sign(sm(t) )］T，其中:

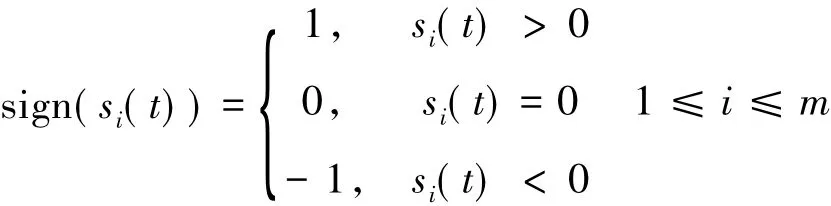
下面给出式(1)在有限时间内到达滑模面上并在其上进行运动的充分条件.

定理1若式(1)满足假设条件(a)－(c)，且其控制输入由式(4)－(7)给出，则式(1)的状态轨线在有限时间内到达滑模面式(3)上.

证明设Lyapunov函数为

且V是正定的.对Lyapunov函数(8)两边关于时间t求导得:

由假设条件(b)及式(7)代入上式并化简可得:

又因为

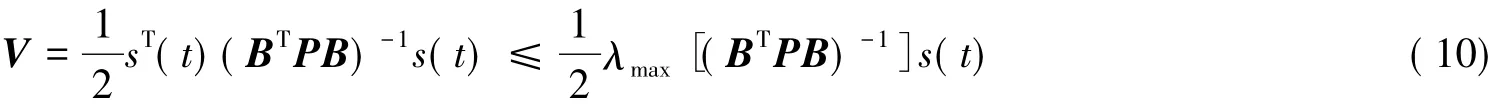
因此，根据文献［9］可知，式(1)的状态轨线在有限时间内达到滑模面式(3)上.证毕.

下一步设计一个稳定的滑模面，使得滑模控制系统在内部参数摄动与外部扰动时保持良好的品质.

定理2设式(1)满足假设条件(a)－(c)，如果存在正定阵P＞0，R＞0，Qi＞0，(i=1，2，…，k)及正常数μ、μi，(i=1，2，…，k)，且满足线性矩阵不等式:

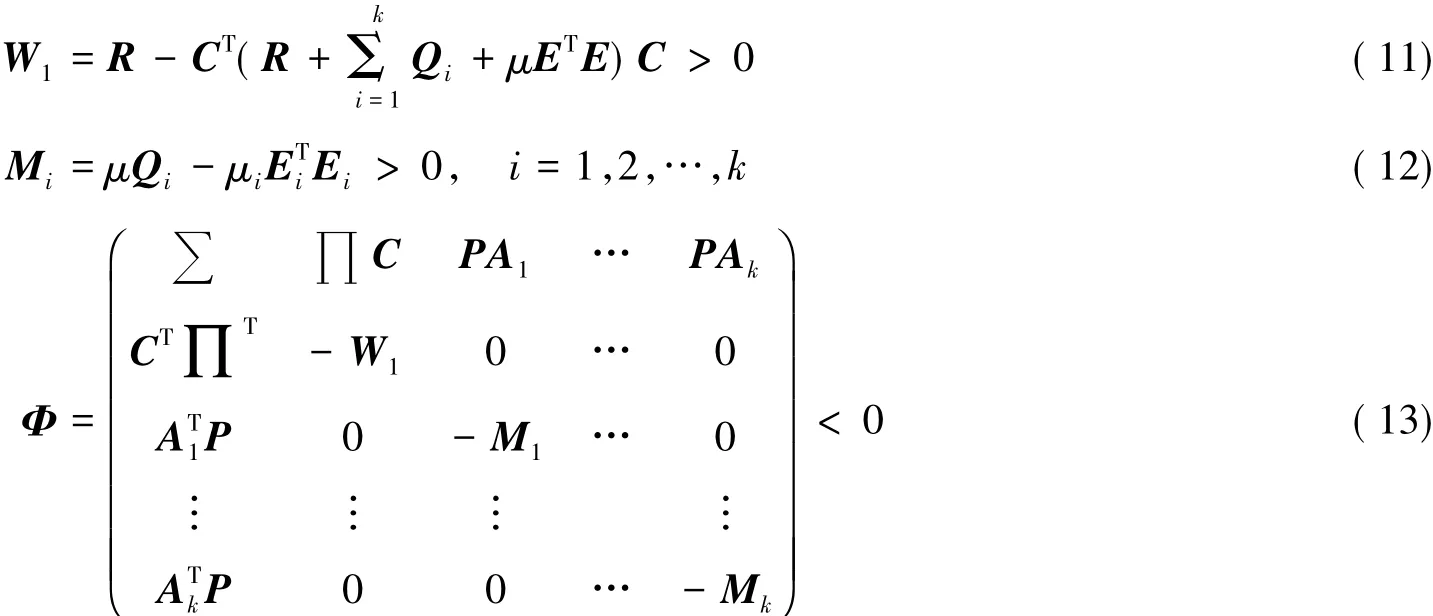
其中

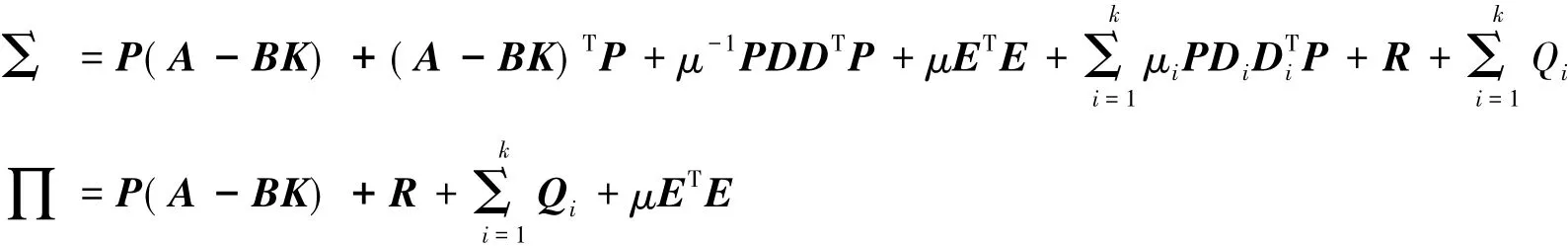
则在滑模面方程式(3)下，滑模控制率式(4)－(7)使得闭环系统是渐进稳定的.

证明由题意可构造Lyapunov函数为

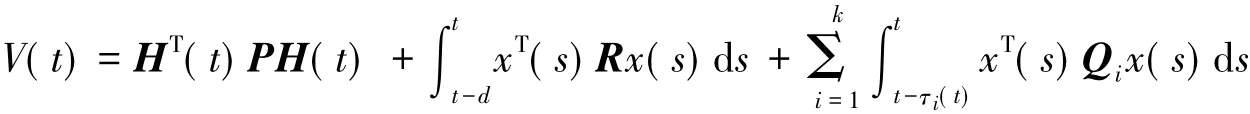
其中P，R，Q1，…，Qk为正定矩阵，H(t) = x(t)－Cx(t－d).将上式两边关于t求导并将式(1)及式(4)代入可得:

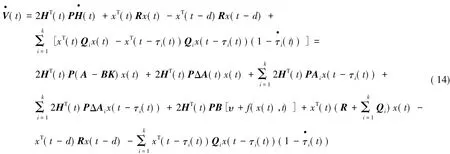
由滑模面方程式(3)可知:s(t) = 0

因此有:

根据引理2和假设条件(b)可知:存在正常数μ、μi，i=1，2，…，k.使得下列式子成立:

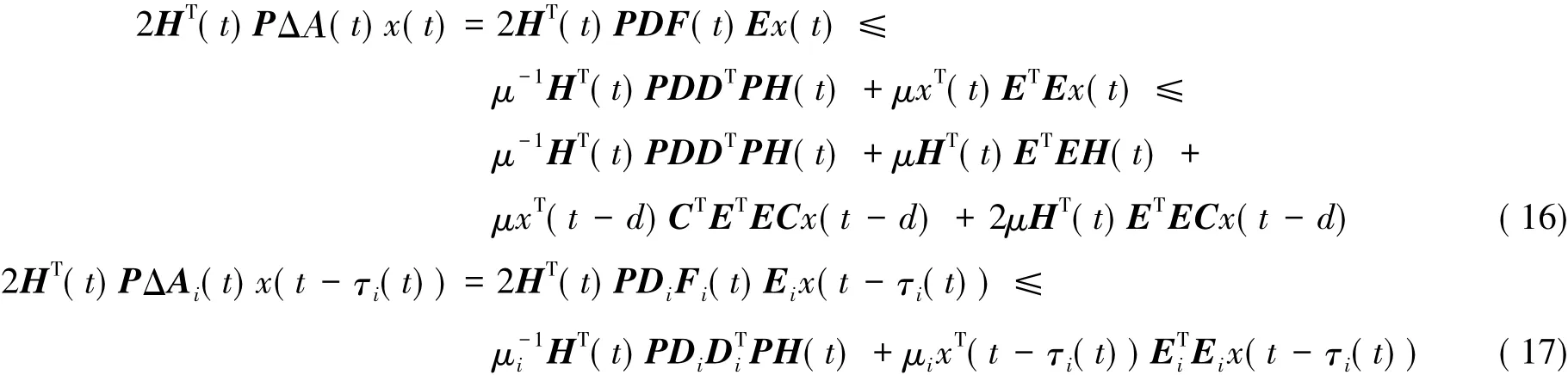
其中i=1，2，…，k.

又易知:

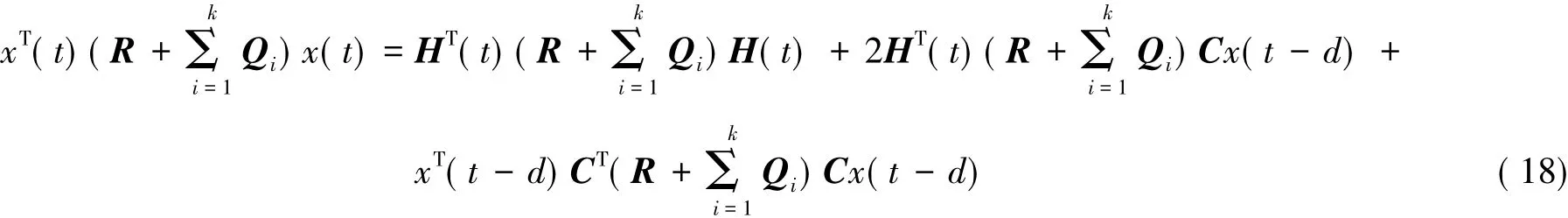
因此，将式(15)－(18)代入式(14)并化简可得:

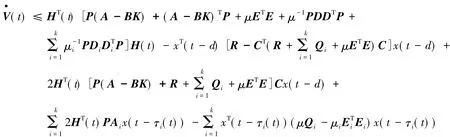
令σ=(H(t)，x(t－d)，x(t－τ1(t) )，…，x(t－τk(t) ) )T，再根据定理已知条件可得(t)≤σTΦσ.又由于Φ＜0为负定矩阵.从而，由文献［10］的定理9.8.1可知:在滑模面方程式(3)下，滑模控制率式(4)－(7)使得闭环系统是渐进稳定的.

注根据定理2可知，利用构造Lyapunov函数的方法给出了闭环系统渐进稳定的一个充分条件，充分条件以线性矩阵不等式的形式给出.因此，当线性矩阵不等式是可行的时候，则由式(3)给出的滑模面的设计及由式(4)－(7)给出的控制率的构造保证了式(1)的状态轨线能在有限时间内到达滑模面上并在其上保持运动.

参考文献:

［1］UTKIN V I.Variable Structure Systems with sliding mode［J］.IEEE Trans Automat Cont，1977，26(2):212-22

［2］KHAZALI E R.Variable Structure Robust Control of Uncertain Time-Delay Systems［J］.Automatica，1998，34 (3):327-332

［3］高为炳.变结构控制理论基础［M］.北京:科技出版社，1990

［4］员陈鑫，蒋威.具外部扰动的变时滞不确定奇异系统的滑动模态控制［J］.纯粹数学与应用数学，2012，28(4):531-539

［5］LIEN C H.Delay-dependent and Delay-independent Guaranteed Cost Control for Uncertain Neutral Systems with Time-varying Delays Via LMI Approach［J］.Chaos Solitons and Fractals，2007，33(3):1017-1027

［6］NIU Y，WC H D，LAM J.Robust Integral Sliding Mode Control for Uncertain Stochastic Systems with Time-varying Delay［J］.Automatica，2005，41(5):873-880

［7］YOUGUO H，MUYONG Z.Sliding Mode Control for a Class of Uncertain Neutral Delay Systems［J］.Procedia Engineering，2011，(15):1181-1185

［8］NIU Y，LAM J，WANG X.Sliding-mode Control for Uncertain Neutral Delay Systems IEE Proc［J］.Control Theory Appl，2004，151 (1):38-44

［9］JIA F，JIANG W.Sliding Mode Control for Fractional Differential Systems with State-delay［J］.Chin.Quart.J.of Math.2012，27 (1):117-122

［10］HALE J K，VERDUYN L S M.Introduction to Functional Differential Equations［M］.New York:SpnngerVerlag，1993

Sliding Mode Control of Uncertain Neutral System with
Multiple Time-varying Delays

DONG Cui-li，JIANG Wei
(School of Mathematical Sciences，Anhui University，Hefei 230601，China)

Abstract:This paper mainly researches the sliding mode control of uncertain neutral system.The system involves multiple time-varying delays and nonlinear external perturbations.A sliding surface is designed based on the current state and delayed state.The design of the sliding mode controller guarantees that the trajectory of system can be driven onto the sliding surface in a finite time and maintains moving on it.By the Lyapunov function，a sufficient condition given in the form of linear matrix inequality for asymptotic stability of the closed-loop system is obtained.

Key words:neutral time-varying delays systems; sliding mode control; linear matrix inequality

中图分类号:O231.2

文献标识码:A

文章编号:1672－058X(2015) 08－0019－05

doi:10.16055/j.issn.1672－058X.2015.0008.005

收稿日期:2015－01－03;修回日期:2015－02－21.

*基金项目:国家自然科学基金(11371027).

作者简介:董翠丽(1990-)，女，安徽阜阳人，硕士研究生，从事泛函微分方程及控制论研究.