OFDM信号压缩采样重构算法的FPGA实现

苗长云，沈广平，戈立军（天津工业大学电子与信息工程学院，天津　300387）



OFDM信号压缩采样重构算法的FPGA实现

苗长云，沈广平，戈立军
（天津工业大学电子与信息工程学院，天津300387）

摘要：针对OFDM信号压缩采样重构的优化正交匹配追踪（OOMP）算法，提出了一种基于FPGA的OOMP算法实现方案.该方案将算法分为并串变换、求系数、解方程3个步骤，在Altera公司Stratix IV系列FPGA芯片EP4SE530F43C2上采用多时钟控制的乘法器级联SRAM结构，实现了矩阵向量相乘，节约了存储资源；在Quartus II开发环境下采用VHDL语言编写了OOMP算法程序，并采用Modelsim软件对其进行了门级时序仿真，实现了OOMP算法.仿真结果表明：该方案具有复杂度低、处理速度快等优点.

关键词：优化正交匹配追踪算法；现场可编程门阵列；乘法器；SRAM；硬件描述语言

随着人们对通信信息量需求的日益增大，为了满足未来不断增长的数据传输速率的要求，增加系统带宽来提高传输速率是直接有效的方法，而超宽带（UWB）通信系统的大带宽具有在提高传输速率方面明显优势[1]. 3～10 GHz是首个支持UWB通信的频段，最高支持数据传输速率480 Mbps；60 GHz频段系统则可实现高于5 Gbps传输速率的超高速无线数据传输.现有的3～10 GHz标准、60 GHz标准超宽带系统均规定OFDM是实现超宽带的高速无线个域网的物理层方案之一，并且OFDM-UWB具有频带利用率高、抗符号串扰能力强、抗频率选择性衰落能力强等优点，研究基于OFDM-UWB系统具有重要的应用价值.而高速采样ADC是OFDM-UWB系统面临的首要挑战与技术瓶颈，根据香农-奈奎斯特采样定理，无失真地恢复原始信号，要求采样频率至少是输入信号频率2倍以上才能实现.

针对此问题，文献[1]提出并行压缩采样（PSCS），并采用传统正交匹配追踪（OMP）算法重构压缩采样后信号；文献[2]基于OFDM信号频域稀疏位置已知的特点，提出扩展并行压缩采样（EPSCS），并采用优化正交匹配追踪（OOMP）算法重构信号.目前国内外的压缩采样重构的FPGA实现都是基于文献[1]中传统OMP算法.基于传统OMP算法，文献[3]采用一种动态流水线结构，加法器级联RAM实现乘积的随加随存，不断存储更新最大列的结构；文献[4]采用多RAM存储数据的地址及数据，简化矩阵求逆的复杂度的结构.这些传统OMP算法方案对于硬件资源有诸多浪费，需不断寻找乘积最大列，最大列矩阵会随着残差不断更新变的越来越大，并在求残差时，在FPGA硬件实现中需对最大列矩阵求逆[5]，使实现变得异常复杂.

针对文献[2]提出的用于EPSCS的OOMP算法，本文提出了一种基于FPGA的OOMP算法实现方案，可将原先硬件矩阵求逆运算转变成解方程的乘除运算[6]，而乘除运算在FPGA有固定模块.该方案在Altera公司Stratix IV系列FPGA芯片EP4SE530F43C2上采用多时钟控制的乘法器级联SRAM结构，实现矩阵向量相乘，节约了存储资源；在Quartus II开发环境下采用VHDL语言编写了OOMP算法程序，并采用Modelsim软件对其进行门级时序仿真，实现了OOMP算法.

1　算法原理

1.1 OFDM信号模型

在OFDM系统中，频域信号X=[X0，X1，…，XN-1]T通过N个相互正交的子载波进行传输，其中第k个子载波上的数据Xk为PSK、QAM[7]等数字映射的结果，则经过IDFT调制的时域信号可表示为

定义向量x = [x0，x1，…，xN-1]T，则（1）式可表示为矩阵形式

式中：z = [z0，z1，…，zN-1]T为N×1维高斯白噪声.经过DFT[8]解调所得频域信号可表示为

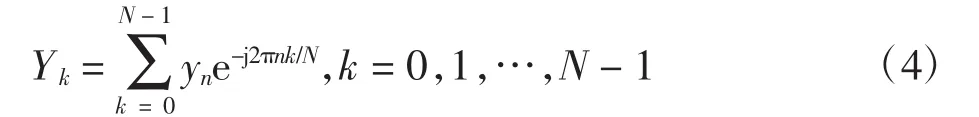
定义向量Y = [Y0，Y1，…，YN-1]T，则将（4）式写为矩阵形式

式中：QH为N×N维傅里叶变换矩阵[9]；Z = QHz为高斯白噪声的频域形式.

1.2 PSCS原理

PSCS是基于随机解调[10]（RD）的压缩采样原理的延伸，其相当于将RD结构扩展为多行：

式中：Φi（t）[11]为以奈奎斯特频率变化的取值为±1的伪随机序列；P为路数；S为段数；M为总的观测值数量，M = SP.传统信号重构算法[12]从少量观测信号中恢复信号，如图1所示.在总观测点数相同的情况下，PSCS结构中的采样速率为RD的1/P，即PSCS以复杂度的提升换取采样速率的降低，对于不稀疏的OFDM信号可达到降低采样速率的效果.

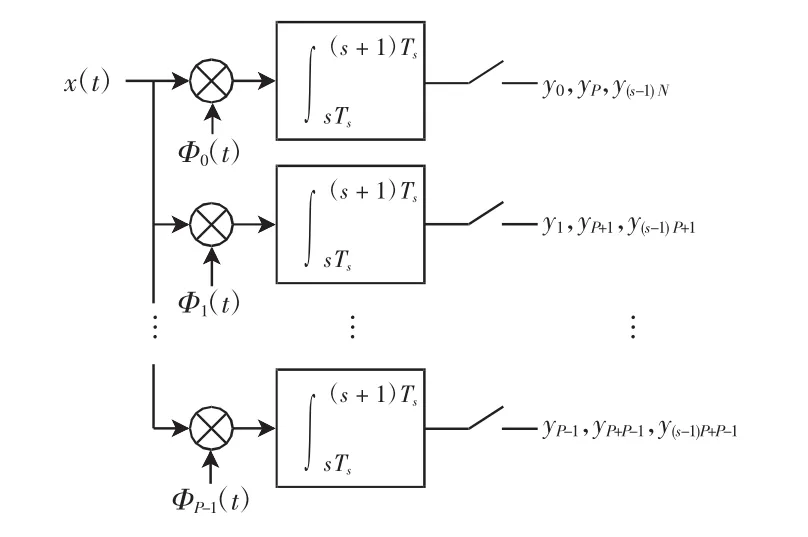
图1　PSCS框图Fig.1 PSCS algorithm block diagram

1.3 OOMP算法原理

OOMP算法是基于传统OMP[13]算法的一种延伸，对传统OMP算法做了最优化处理，如图2所示.输入为压缩采样得到测量值向量y，长度为M，观测矩阵V是满足一定条件的M×N伪随机序列，在已知迭代次数K的情况下[14]，得到稀疏位置的系数Ck为

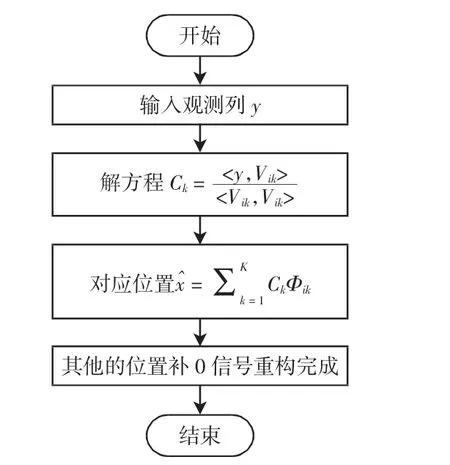
图2　OOMP算法流程图Fig.2 Optimized OMP algorithm flow chart

已知OFDM信号基矩阵Ψ的稀疏位置，可以恢复原始信号的非稀疏位置，并在稀疏的位置上补零[15]，得到重构信号

2　OOMP算法实现方案

本设计选用Altera公司Stratix IV系列FPGA芯片P4SE530F43C2，设计在Quatrus II软件开发环境下进行，用Modelsim进行了相应的功能仿真.将FPGA实现的过程分成3部分：并串转换、求系数、解方程，实现原理框图如图3所示.

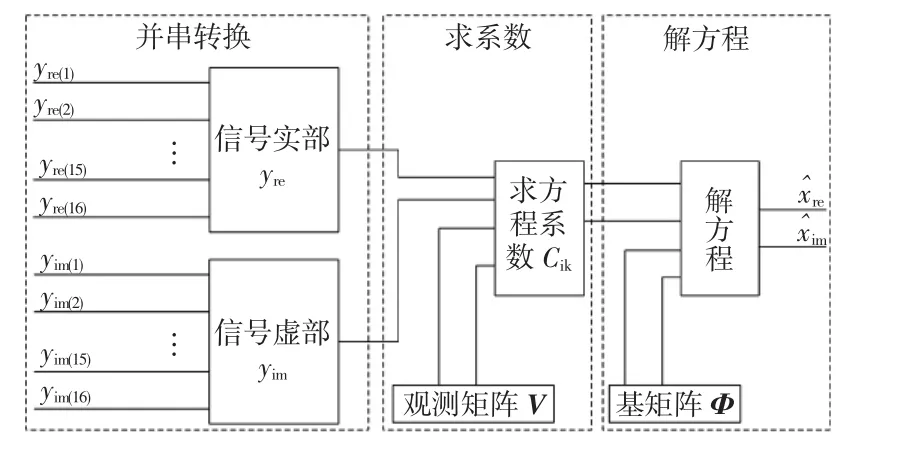
图3　优化OMP原理框图Fig.3 Functional block diagram of optimized OMP

构建只读存储器ROM1、ROM2、ROM3和ROM4. ROM1用来存储测量矩阵实部，ROM2存储测量矩阵虚部，ROM3用来存储基矩阵实部，ROM4存储基矩阵虚部.乘法器级联SRAM的乘累加器结构是实现本设计思路的重要载体，它由有符号数复数乘法器、延时SRAM和求和减法器组成，复数乘法器相乘值做SRAM延时输入和求和减法器加项输入，SRAM延时输出做求和减法器负项输入，求和减法器输出接回求和减法器做正项输入，正项输入求和减负项输入得到累加和.原始OFDM信号经PSCS压缩采样后输入信号是复数信号，长度N = 165，稀疏度K = 112，总采样点M = 160，并行路数P = 16，分段数S = 10.

2.1并串转换

并串联设计转换如图4所示.并串转换各模块中，控制单元用来产生整个并串模块的时钟clk、clk_r 和clk_112；数据写入模块是将16路并行的PSCS采样后OFDM信号按时钟clk_r写入，同时以clk时钟读出，clk是clk_r的16倍，通过读写时钟的不同实现16路并行输入PSCS采样点串行1路输出采样点，相当于压缩采样（CS）1路信号；地址产生器分配数据读写地址；数据存储器实现按行存入经过并串转换输出的数据，并根据地址产生器产生的读地址读数据，向量与矩阵相乘需多次读出向量非稀疏的位置与矩阵求内积，向量写入时钟是clk，读出时钟clk_112，128*clk= 160*clk_112，实现写入160抽样点，读出128个抽样点；写使能产生器是在采用乒乓操作读写RAM中的数据时，使读写在2个RAM中分别同时进行.

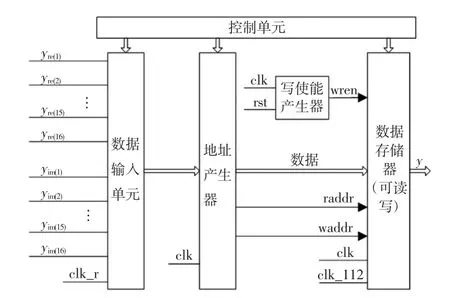
图4　串并转换设计图Fig.4 Design diagram of equation solution

2.2求系数

FPGA中实现求系数的硬件设计，如图5所示.时钟模块产生数据处理所需要的时钟，采用clk_112和clk_160，clk_112=160*clk_160，实现160次累加；数据存储器存储并串转换后数据y，虚部和实部分开存储；模块地址产生器用来产生测量矩阵地址addrv；测量矩阵存储按列存储测量矩阵V，虚部和实部分开存储；延时共轭器是对测量矩阵延时并对复数求共轭得number1*；乘加器实现求乘累加，乘加器1实现测量矩阵V与y数据的乘累加运算，乘加器2实现测量矩阵自乘累加运算；共轭器对输出结果求共轭；除法器用来做除法运算，除法器1实现乘加器1与乘加器2除法运算，除法器2实现除法器1两倍余数与乘加器2的除法运算，进而得到数据除法四舍五入的进位；加法器实现除法四舍五入进位与除法器1值求和，得到Cik.

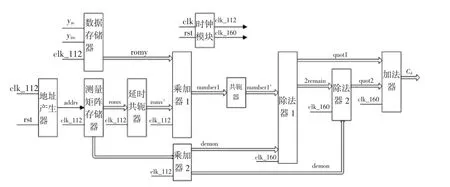
图5　求系数的设计图Fig.5 Design diagramof computing coefficient

2.3解方程

FPGA中实现解方程的硬件设计图如图6所示.

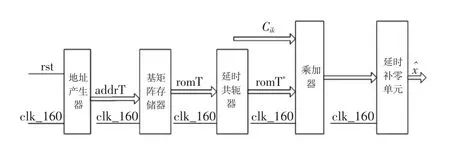
图6　解方程的设计图Fig.6 Design diagram of equation solution

图6中，T为基矩阵Φ，地址产生器用来产生基矩阵的地址addrT；基矩阵存储器按列存储，虚部和实部分开存储；延时共轭器用来对基矩阵求共轭来做矩阵相乘；乘加器用来做乘累加和，完成矩阵系数Cik与基矩阵乘累加和，得到延时补零单元用来对得到数据的稀疏的位置补零.

3　FPGA仿真及结果分析

数据处理时，对数据值做一定比例放大，根据读写时钟变换完成输入数据并串变换得到y实部和虚部y_re和y_im，V_re和V_im是存储在ROM1和ROM2中观测矩阵V实部和虚部，如图7所示. z6是y与V做内积得到虚部，矩阵V自内积只有实部z7，Cik_re 和Cik_im是求方程系数实部和虚部如式（7），z6除以z7结果延迟一个时钟clk_160得到Cik_im，如图8所示，T_re和T_im是存储在ROM3和ROM4中基矩阵Φ实部和虚部，如式（8）Cik和Φ相乘得到实部和虚部是z12和z13，z12和z13累加得z14和z15，如图9所示.

图7　仿真结果1Fig.7 Simulation result 1

图8　仿真结果2Fig8 Simulation result 2

图9　仿真结果3Fig9 Simulation result 3

将得到结果与Matlab中OFDM原始信号的数据做比较，如图10所示，在OOMP算法的FPGA实现方案中，恢复数据保持了原OFDM信号数据的结构特征，数据重构比较理想. FPGA硬件资源消耗见表1，可知本方案与文献[3]所使用的方法相比，少用2 648个LE.该方案具有处理速度快、实现简便和占用较少的硬件资源等优点.

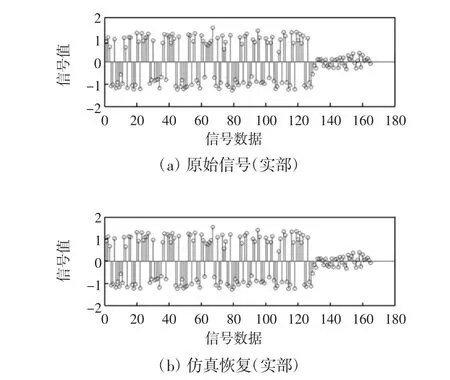
图10　恢复信号与输入信号的对照图（信号的实部）Fig.10 Contrast diagram of reconstruction signal and input signal（real component of signal）

表1　FPGA硬件资源消耗Tab.1 Hardware resources consumption of FPGA

4　结语

本文提出了一种基于FPGA的OOMP算法实现方案.该方案在FPGA芯片EP4SE530F43C2上实现了矩阵向量相乘，节约了存储资源；在Quartus II开发环境下，采用VHDL语言编写了OOMP算法程序，并采用Modelsim软件对其进行了门级时序仿真，实现了OOMP算法.本方案具有实现复杂度低、处理速度快等优点，主要针对稀疏信号，对于实际信号传输有很重要的意义.本文没有对非稀疏信号进行处理，但非稀疏信号可经过变换域转换为稀疏信号，并通过OOMP算法进行处理，这将是今后一个重要的研究方向.

参考文献：

[1] MISHALI M，ELDAR Y C，ELRON A J. Xampling：Signal acquisition and processing in union of subspaces [J]. IEEE Transaction on Signal Processing，2011，59（10）：4719-4734.

[2] YU Z，HOYOS S，SADLER B M. Mixed-signal parallel compressed sensing and reception for cognitive radio[C]//33th IEEE International Conference on Acoustics，Speech and Signal Processing. Las Vegas：IEEE，2008：3861-3864.

[3]刘颖，苗长云，厉彦峰.基于FPGA的网络电话终端的研究[J].天津工业大学学报，2009，28（1）：75-78. LIU Y，MIAO C Y，LI Y F. Design of terminal unit in IP net telephony system based on FPGA [J]. Journal of Tianjin Polytechnic University，2009，28（1）：75-78（in Chinese）.

[4] BLACHE P，RABAH H，AMIRA A. High level prototyping and FPGA implementation of the orthogonal matching pursuit algorithm[C]// 11th International Conference on IEEE. Montreal：IEEE，2012：1336-1340.

[5]陈伟凯.基于压缩的OFDM系统稀疏信道估计理论研究[D].天津：天津大学，2012. CHEN W K. Research on compressive sensing based sparse channel estimation in OFDM systems[D]. Tianjin：Tianjin University，2012（in Chinese）.

[6]何雪云，宋荣芳，周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究[J].南京邮电大学学报：自然科学版，2012，30（2）：60-65. HE X Y，SONG R F，ZHOU K Q. Study of compressive sensing based sparse channel estimation in OFDM systems[J]. Journal of Nanjing University of Posts and Telecommunications: Natural Science，2012，30（2）：60-65（in Chinese）.

[7]姚航.基于压缩感知的OFDM系统稀疏信道估计研究[D].西安：西安电子科技大学，2014. YAO H. Research on channel estimation techniques based on compressed sensing in OFDM systems [D]. Xian：Xidian University，2014（in Chinese）.

[8]韩林，王正彦，孟南南.压缩感知理论及OMP算法FPGA实现研究[J].工业控制计算机，2014，27（1）：76-78. HAN L，WANG Z Y，MENG N N. Compressed sensing theory and OMP algorithm by FPGA [J]. Industrial Control Computer，2014，27（1）：76-78（in Chinese）.

[9]方标，黄高明，高俊，等.一种分段分块式压缩采样模型的设计[J].西安电子科技大学学报：自然科学版，2014，41 （4）：151-157. FANG B，HUANG G M，GAO J，et al. Design of a segmented and blocked compressive sampling model[J]. Journal of Xidian University：Natural Science，2014，41（4）：151-157（in Chinese）.

[10] AGRAWAL T，LAKKUNDI V，GRIDDIN A，et al. Compressed sensing for OFDM UWB systems[C]// 2011 IEEE Radio and Wireless Symposium. Phoenix：IEEE，2011：190-193 （in Chinese）.

[11] KIROLOS S，LASKS J，WAKIN M，et al. Analog-to-Information conversion via random demodulation[C]//2006 IEEE/ Dallas/CAS Workshop on Design，Application，Integration and Software. Richardson：IEEE，2006：4.

[12]张弓，文方青，陶宇，等.模拟-信息转换器研究进展[J].系统工程与电子技术，2015，37（2）：229-238. ZHANG G，WEN F Q，TAO Y，et al. Advances in analog-toinformation convertor [J]. Systems Engineering and Electronics，2015，37（2）：229-238（in Chinese）.

[13]孟南南.压缩感知算法的FPGA实现[D].青岛：青岛大学，2013. MENG N N. The FPGA implementation of compressed sensing algorithm[D]. Qingdao：Qingdao University，2013（in Chinese）.

[14]吴浩.基于随机解调的压缩采样与波形重构的实现[D].成都：电子科技大学，2013. WU H. Realization of compression samplong and the waveform reconstruction based on the random demodulation. [D]. Chengdu：University of Electronic Science and Technology of China，2013（in Chinese）.

[15]黄晓霞.基于压缩采样的模拟到信息转换的研究与实现[J].软件导刊，2011，10（8）：19-21. HUANG X X. Research and implementation of analog-to-information conversion in compressive sensing [J]. Software Guide，2011，10（8）：19-21（in Chinese）.

FPGA implementation of compression sampling reconstruction algorithm based on OFDM signal

MIAO Chang-yun，SHEN Guang-ping，GE Li-jun
（School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Abstract：According to optimized orthogonal matching pursuit（OOMP）algorithm in the compressed sampling reconstruction of OFDM signal，a scheme of OOMP based on FPGA is proposed. The scheme divides the algorithm into parallel-serial conversion，computing coefficient and solving equation. In Altera′FPGA Stratix IV EP4SE530F43C2，matrix -vector multiplication is implemented in the cascade structure of multiplier and SRAM，which is controlled by multiple clocks，to save resources. In the Quartus II environment，the scheme programs OOMP with VHDL. The scheme uses Modelsim to carry out gate -level timing simulation and implements OOMP algorithm correctly. The simulation results show that the scheme has the advantages of easy implementation and high processing speed.

Key words：optimized orthogonal matching pursuit algorithm；FPGA；multiplier；SRAM；VHDL

通信作者：苗长云（1962—），男，教授，博士生导师，主要研究方向为光通信及光传感技术.E-mail：miaochangyun@tjpu.edu.cn

基金项目：国家自然科学基金资助项目（61302062，51274150）；天津市应用基础及前沿技术研究计划青年基金项目（13JCQNJC00900）

收稿日期：2015-10-28

DOI：10.3969/j.issn.1671-024x.2016.02.012

中图分类号：TN914.4

文献标志码：A

文章编号：1671－024X（2016）02－0060－05