“坐标系中三角尺滑动”的教学与反思

☉江苏省泗洪县第三中学 刘俭红

“坐标系中三角尺滑动”的教学与反思

☉江苏省泗洪县第三中学 刘俭红

在最近一次中考复习教研活动中，笔者有幸执教了一节“坐标系中三角尺滑动”的教学研讨课，得到与会老师的好评，本文呈现这次活动的教学流程和预设意图，与更多同行研讨交流.

一、课例教学流程

活动一：三角尺摆放到坐标系.

操作与思考：将一条直角边落在坐标轴上，且使其中一个顶点与原点重合，求落在第一象限内的那个顶点的坐标.

预设意图：通过在平面直角坐标系下摆放特殊直角三角形，让学生复习坐标系下特殊点的坐标的求法；由于问题答案开放，如图1、图2，可以让不同小组汇报他们的摆放方式和解法，达到学生全员参与的效果.

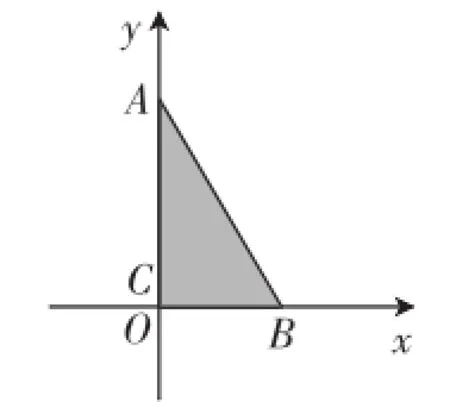
图1

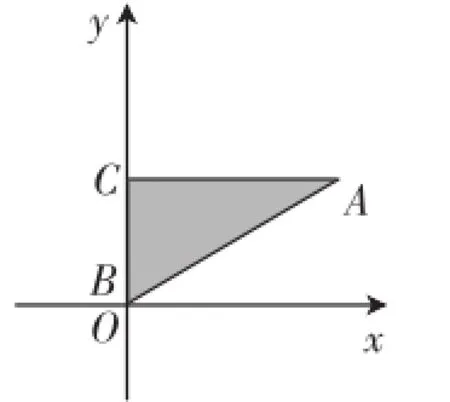
图2

活动二：换个方式再摆放.

操作与思考：将斜边落在坐标轴上，且使其中一个顶点与原点重合，求落在第一象限内的那个顶点的坐标.

预设意图：摆放方式不唯一，如图3，斜边落在坐标轴上后，求第一象限内的顶点的坐标则需要向坐标轴引垂线段（CG⊥AB于点G），构造Rt△BCG求解，比前一种摆放式要增加了解题层次，引导学生复习“射影定理”及其性质，并灵活写出点的坐标，为后续变式研究打下基础.

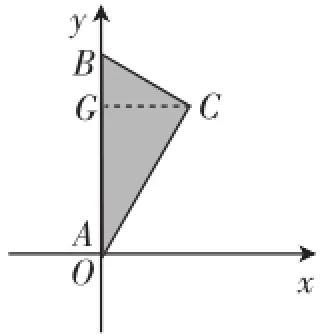
图3

活动三：滑动三角尺.

操作与思考：将含30°的直角三角尺（△ABC）放在如图4所示的直角坐标系中，点B（0，4），∠BAC=30°，将△ABC中的点B沿y轴向下运动，点A沿x轴的正半轴运动.

（1）当点B运动到原点O时，直接写出点C的坐标（_____，_____）；

（2）当点B向下运动1个单位时，求出此时点C到原点O的距离；

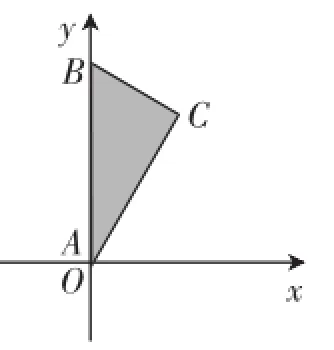
图4

（3）当点B向下运动到达点D（0，-4）时，求点C走过的路径长.

预设意图：前两问属于预热阶段，第（1）问与上一个操作活动相呼应，学生应该很快能写出点C的坐标（1，；第（2）问，让学生体验向下平移一个特殊单位后，图形的位置会发生怎样的变化（如图5），而这种位置也是一个特殊的位置状态（BC⊥y轴，AC⊥x轴），此时点C距离原点也获得了最大值；第（3）问要确定点C的运动起点、终点、运动路径，可以通过观察、想象、作图来判断.从前两问可以发现两种不同位置状态下点C的坐标分别为（1，，（2，2），这时就能有个直觉，貌似在一条直线上，沿这个方向继续验证、思考就能获得突破.

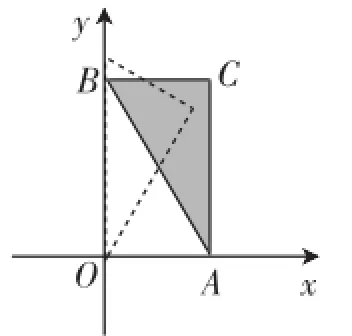
图5

下面预设几种不同的探究思路：思路一：基于“四点共圆”角度，如图6，由于Rt△AOB与Rt△ACB是共斜边的直角三角形，以AB为直径的圆满足点A、O、B、C四点共圆，连接OC，根据圆周角性质可知∠BOC=∠BAC=30°，即OC与y轴的夹角恒等于30°.于是可以判定点C走过的路径应该是一条线段！接下来再判断点C，再结合第（2）问中点C到原点的距离，发现这是在第一象限内点C到原点的最大距离4；相应地，当点C落在第三象限时，也有一个最大距离4，所以点C走过的路径长为4+4=8.

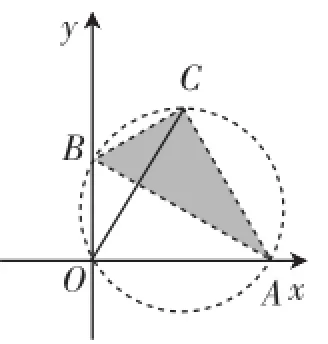
图6

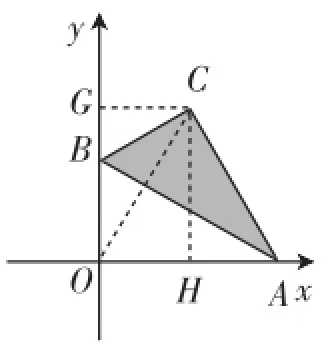
图7

思路三：基于“直线斜率”角度，仍然利用图7，从直线OC的斜率角度思考也可获得解释.

完成上述思路突破之后，可链接一道结构相同的考题，如2015年1月湖北省武汉市九年级调研试卷中填空题第16题：

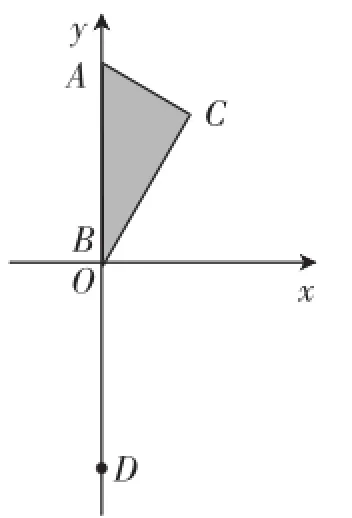
图8

如图8，将含30°的直角三角尺放在如图8所示的直角坐标系中，点A（0，4），点B在原点，∠C=90°，∠ABC= 30°，D点与A点关于原点对称，A点向D点运动，到达D点后停止.B点在x轴的正半轴上运动.当点A到达点D时，点C走过的路径长为________.

活动四：换另一种三角尺再研究.

刚才研究了含30°的三角尺在坐标系中的摆放与滑动，我们知道还有另一个含45°的三角尺，下面来研究它在坐标系中的摆放与滑动问题.

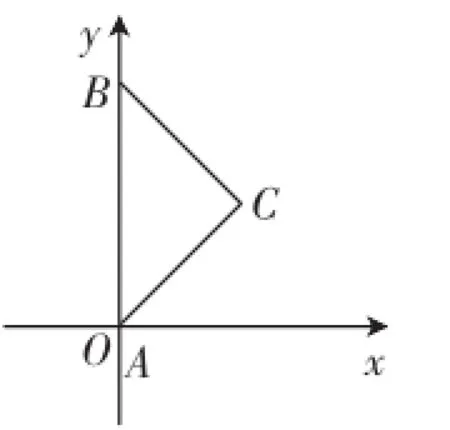
图9

操作与思考：将含45°的直角三角尺（△ABC）放在如图9所示的直角坐标系中，点B（0，4），∠BAC= 45°，将△ABC中的点B沿y轴向下运动到（0，-4）为止，同时，点A沿x轴的正半轴运动.

（1）当点B运动到原点时，直接写出点C的坐标（_____，_____）；

（2）在运动过程中，求第一象限内的点C到原点的最大距离；

（3）当点A运动到点（2，0）时，求此时点B的坐标.

预设意图：前两问与之前的操作活动类似，解答思路容易发现.第（3）问需要分类讨论，学生可能容易漏解，这时可启发他们构造出图10的两种情况，就容易发现Rt△AOB或Rt△AOB′是含30°的特殊直角三角形，从而问题获解.事实上，如果课堂时间充足，还可引导学生自主设计问题，比如此时能否求出点C的坐标？

二、教学立意与教后反思

上面我们就各个教学环节给出了相应的教学预设，重点从操作的角度进行了介绍，以下再从整节课的教学立意和教后反思的角度进一步做出阐释.

1.追求简约的复习课教学取向

受到应试复习的影响，当前中考复习课整体以大量例习题堆砌为主，过分追求针对某个知识点或方法的例习题全方面、多角度覆盖，从而使得课堂容量偏大，多数学生在课堂上难以接受或完全消化，在很多复习课堂上，常常见到的是教师或少数优秀学生轮番讲解、展示，而大多数学生常常对有些较难的例题还没有真正读懂题意，就被牵引着看、听解法，使得“探索未知世界”式的数学学习又成为了“参观式学习”.这也是我们预设上述课例的一个教学立意，即追求简约的复习课堂教学取向，使得更多的学生从较低的台阶出发，拾级而上，同时又让不同的学生在课堂上达到不同的高度或知识理解的深度.

2.从开放题到开放的数学教学

所谓“开放题”，首先想到的可能就是“开放题”相对应的那种“具有唯一正确答案，甚至唯一正确解题方法的传统问题（封闭题）”.在“百度百科”上检索“开放”一词，有如下丰富的解释：比如释放；敞开、允许入内；张开、舒展；使关闭着的打开；发射；解除封锁、禁令、限制；思想开通、解放等.上文课例中的前两个数学活动都是开放题，而通过这些开放题设计的真正意图是追求开放的数学教学，使得课堂上学生真正成为问题解决和研究的主人，让他们参与问题的探索、生成、生长、拓展等，并由此展开对话、追问，从而也就追求了开放的数学教学.

1.刘东升，符永平.从“封闭”走向“开放”——2013年中考命题的“另类解析”与教学导向［J］.中学数学（下），2013（10）.

2.郑毓信.开放题与开放式教学［J］.中学数学教学参考，2001（3）.

3.郑毓信.再论开放题与开放式教学［J］.中学数学教学参考，2002（6）.

4.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.

5.【日】佐滕学.21世纪学校改革的方向［J］.人民教育，2014（1）.

6.王光明，廖晶.“探索世界”范式及其对数学教育的启示——ICME12获奖报告述评［J］.课程·教材·教法，2013（12）.