统计收敛与Lacunary统计收敛

鲍玲鑫， 官明友

(福建农林大学计算机与信息学院, 福建 福州 350002)

统计收敛与Lacunary统计收敛

鲍玲鑫， 官明友

(福建农林大学计算机与信息学院, 福建 福州 350002)

针对Lacunary统计收敛与经典统计收敛的相容性问题，利用统计测度理论证明了Lacunary统计收敛与经典统计收敛等价的充分必要条件是相应的Lacunary序列是几何递增的.

统计收敛； Lacunary统计收敛； 统计测度； 半范数

0 引言

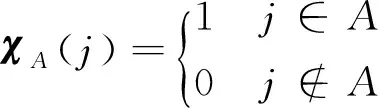
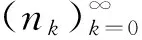
程立新等[6-7]利用几何泛函分析与Banach空间理论引入了统计测度理论, 并证明了各种具体形式的统计收敛均可用相应的一族统计测度收敛加以刻画. 给定一族统计测度S, 集合A⊂N称为S-零测集是指μ(A)=0对一切μ∈S成立. Banach空间X中的序列(xn)称为测度S-收敛于x∈X是指对任意的ε>0,A(ε)为S-零测集. 鲍玲鑫等[8]进一步证明了任意一个理想Ι⊂2N, 存在一族统计测度S使得理想Ι-收敛等价于测度S-收敛.

本文的主要目的是利用文献[6-8]的一些结果证明Lacunary统计收敛与经典统计收敛等价的充分必要条件是相应的Lacunary序列是几何递增的.

1 主要结果

本文中的所有记号都是统一的. 字母X表示实Banach空间. 给定A⊆N,A的特征函数χA可以看作是l∞中的一个向量, 记χN=e.

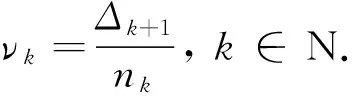
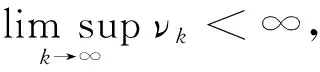
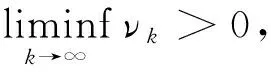
关于Lacunary统计收敛、 统计测度收敛与半范数收敛的结果可参考文献[6-7].

定理1 设(nk)为一个Lacunary序列， 且设(xn)⊂X以及x∈X.

1) 序列(xn)(经典)统计收敛于x当且仅当(xn)测度ΜK-收敛于x.

2) 序列(xn)Lacunary统计收敛于x当且仅当(xn)测度ΜL-收敛于x.

3)A⊂N为ΜK(相应地,ΜL)-零测集当且仅当pK(χA)=0 (相应地,pL(χA)=0). 其中ΜK={x*∘χ(·):x*∈∂pK(e)}及ΜL={x*∘χ(·):x*∈∂pL(e)}.

注1 定理1中关于半范数、 次微分映射与统计测度等概念的进一步了解可以参考文献[6-8].

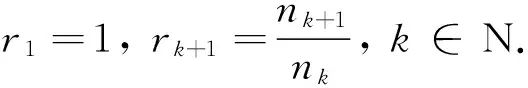
定理2 设(nk)为一个Lacunary序列. 则

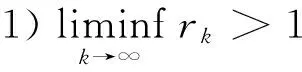
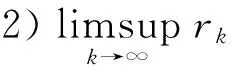
从而有

这与充分性条件相矛盾.

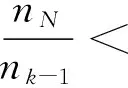
由ε的任意性可知pK(x)≤γpL(x).

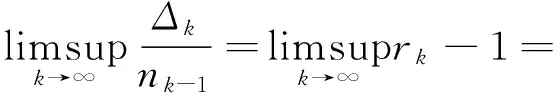
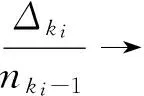
另一方面，

这与充分性条件相矛盾.

推论1Lacunary序列(nk)是几何递增的当且仅当存在两个正数α,β使得在l∞上成立αpK≤pL≤βpK, 或等价地说,pK与pL是相互等价的半范数.

定理3 设(nk)为一个Lacunary序列. 则由(nk)定义的Lacunary统计收敛与经典统计收敛等价的充分必要条件是(nk)为几何递增的.

证明 充分性. 设(nk)为几何递增的. 根据推论1可知, 存在两个正数α,β使得在l∞上成立αpK≤pL≤βpK. 由定理1可知,ΜK与ΜL具有相同的零测集, 即该Lacunary统计收敛与经典统计收敛等价.

必要性. 设由Lacunary序列(nk)所定义的统计收敛与经典的统计收敛等价. 则ΜK与ΜL具有相同的零测集. 根据推论1, 只需证明两个正数α,β使得在l∞上成立αpK≤pL≤βpK. 等价地, 需要证明

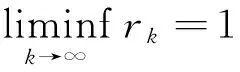
推论2 设(nk)为一个Lacunary序列.

1) 经典统计收敛意味着Lacunary统计收敛当且仅当存在β>0使得pL(x)≤βpK(x)(x∈l∞)成立.

2) Lacunary统计收敛意味着经典统计收敛当且仅当存在α>0使得αpK(x)≤pL(x)(x∈l∞)成立.

[1]FastH.Surleconvergencestatistical[J].ColloquiumMathematicum, 1951, 2(1): 241-244．

[2]SteinhausH.Surlaconvergenceordinaireetlaconvergenceasymptotique[J].ColloquiumMathematicum, 1951, 2(2): 73-74.

[3]ConnorJS.Onstrongmatrixsummabilitywithrespecttoamodulusandstatisticalconvergence[J].CanadianMathematicalBulletin, 1989, 32(2): 194-198.

[4]FridyJA,OrhanC.Lacunarystatisticalconvergence[J].PacificJournalofMathematics, 1993, 160(1): 43-51.

[5]KostyrkoP,SalatT,WilczynskiW.I-convergence[J].RealAnalysisExchange, 2000, 26: 669-689.

[6]ChengLixin,LinGuochen,LanYongyi,etal. Measure theory of statistical convergence[J]. Science China Series(A), 2008, 51(12)： 2 285-2 303.

[7] Cheng Lixin, Lin Guochen, Shi Huihua. On real-valued measures of statistical type and their applications to statistical convergence[J].Mathematical and Computer Modelling, 2009, 50(1/2)： 116-122.

[8] Bao Lingxin, Cheng Lixin. On statistical measure theory[J]. Journal of Mathematical Analysis and Applications, 2013, 407： 413-424.

(责任编辑： 林晓)

On statistical convergence and Lacunary statistical convergence

BAO Lingxin, GUAN Mingyou

(School of Computer and Information, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China)

The purpose of this paper is to investigate problems concerning the equivalence between the Lacunary statistical convergence and the classical statistical convergence. By applying the statistical measure theory, we show that a sufficient and necessary condition for a Lacunary statistical convergence to be equivalent to the classical statistical convergence is that the corresponding Lacunary sequence is geometrically increasing.

statistical convergence; Lacunary statistical convergence; statistical measure; seminorm

2015-09-01

鲍玲鑫(1982-)， 讲师, 主要从事泛函分析方面研究,bolingxmu@sina.com

国家自然科学基金资助项目(11501108, 11426061)； 福建省自然科学基金资助项目(2015J01579)

10.7631/issn.1000-2243.2015.06.0742

1000-2243(2015)06-0742-04

O177

A