基于多特征的纹理特征提取方法研究与应用＊

梅浪奇 郭建明 刘 清

（武汉理工大学自动化学院 武汉430070）

0 引 言

人们对图像的认知主要来自于图像的纹理，颜色和形状。作为图像的基本属性之一，纹理广泛存在于各种自然图像和人工合成图像中，是人们识别和区分各种图像的重要依据［1］。纹理分析技术主要应用在图像识别、图像分类、图像检索、图像分割与合成等领域，这些应用的前提条件就是纹理特征的提取。正因为此，如何快速而有效地提取纹理特征并以之来描述图像已成为国内外研究者的热点方向。

近半个世纪以来，在各种应用中，不同国家的研究人员已经提出了多种纹理特征提取方法。其中较为著名的有灰度共生矩阵（gray level co-occurrence matrix，GLCM）算法［2］、马尔可夫随机场（Markov random field，MRF）模型算法［3］、小波变换 （discrete wavelet transform，DWT）算法［4］、局部二值模式（local binary pattern，LBP）算法［5］等。虽然人们相继提出了各种不同的纹理提取方法，但由于理论与实际的脱节，研究者至今仍然不能找到1种有效的且实用性强的纹理特征提取方法。

目前，人们一方面是对新的方法进行努力探索，另一方面对已有的经典方法进行交叉融合［6］，重点研究纹理特征的旋转不变特性和尺度不变特性。Clausi等［7］提出了1种融合Gabor滤波和GLCM的纹理特征提取算法，能够将Gabor滤波器对中低频纹理信息的捕获能力与GLCM对纹理高频信息的捕获能力结合而在一起，产生较高的特征空间分离并增强纹理识别能力。Acqua等［8］融合了多尺度GLCM方法和半方差图方法，主要用于对雷达图像进行分类。同年，薄华等［9］结合马尔可夫链的性质，从理论上证明了GLCM的计算结果，当像素距离足够大时趋于一致性，为GLCM中的参数简化提供了理论依据。为解决LBP算法忽略了局部纹理之间相互联系得问题，徐少平等［10］于2013年提取了1种基于LBP值对空间统计特征构建的改进纹理描述符ILBP（imporve LBP），融合了 LBP 算法和 GLCM 算法，并有效地提高了图像分类的正确率。

针对现阶段纹理特征提取方法缺乏实用性和稳健性的特点，笔者通过对GLCM算法，LBP算法，DWT算法等不同的纹理特征提取方法的分析比较，对图像检索的反复实验，提出了1种基于多特征的纹理特征提取算法。实验表明，该方法对图像纹理的描述能力更强，并具有一定的普适性。

1 相关工作介绍

1.1 GLCM算法

GLCM算法是由Haralick等在19世纪70年代提出，反映了图像灰度分布关于方向、变化幅度和局部邻域的综合信息。

设f（x，y）为图像在坐标（x，y）处的像素点所对应的灰度值，M，N分别为图像某一邻域的行、列维数。则灰度共生矩阵定义为在图像区域M×N范围内，由2个距离为d且方向为θ的像素组成的像素对在图像中出现的概率，一般记为p（i，j；d，θ）。若设像素对分别为f（x1，y1）＝i和f（x2，y2）＝j，则有

式中：card｛｝为集合中的元素数目。通过改变距离d和角度θ，可以统计不同空间位置的像素对。

灰度共生矩阵已经包含了图像的纹理信息，但由于其数据过多，不利于作为纹理特征。研究者们常常是在其基础上进一步获取二次统计量，并以之作为图像的纹理特征参数。常用的二次统计量有角二阶矩、对比度、熵和相关性［11］。

考虑到图像纹理的灰度共生矩阵多为稀疏矩阵，为了减少 GLCM 的计算量，Unser［12］提出了和差统计法。与灰度共生矩阵不同的是，和差统计法不再用二维向量来表示纹理特征参数，而是用2个一维向量代替，这2个一维向量分别为原矩阵的和向量与差向量。和差统计法能将计算复杂度从原来的ο（L2）变为了ο（L）。灰度级L越大，这种计算优势越明显。

由灰度共生矩阵的定义可知其有4个变量：移动窗口的大小M×M、灰度级L、像素对方向θ和距离d。通常θ是取0°，45°，90°，135°这4个值，得到特征参数后再求平均。而d、M和L的取值则应视实际纹理图像而定。笔者通过大量的实验，研究了ASM、CON、COR和ENT随d、M、L这3个变量的变化规律，获得各变量取值的经验区间和一般原则，见表1［13］。

表1 GLCM中各变量取值的经验区间和一般原则Tab.1 Experiential interval and general principles of the value of each variables in GLCM

1.2 LBP算法

LBP算法最初是由Ojala等［14］提出并用来辅助性的度量图像纹理的局部对比度，它是1种基于灰度的纹理度量。该算法的基本原理是：对于原图像的1个3×3的窗口，以中心像素为阈值并与其邻域像素进行比较，如果邻域像素值比中心像素值大，则将该邻域像素点赋值为1，否则赋值为0；最后给阈值处理后的邻域的每1个像素点赋1个权重，按权重累加得到中心像素的LBP码值并用此值来表示局部纹理特征。其计算过程见图1。

图1 LBP基本原理Fig.1 The basic principle of LBP

LBP基本原理无法提取大尺寸图像纹理的特征。为了解决这个问题，Ojala等［15］提出了用圆形邻域（P，R）来代替原来的3×3邻域，其中：P，R分别表示该邻域中的像素个数和半径，通常记作LBPP，R。邻域的像素点通常是在圆形邻域的边缘上均匀取点。常见的 LBP算子有LBP8，1，LBP16，2和 LBP24，3。

给定1个图像局部区域，计算出该局部区域内每1个像素点的LBP码，继而得到该局部区域的纹理特征分布图，统计其LBP值的直方图就可以得到该局部的纹理特征。

LBP算法最大的特点是计算复杂度小，并且对纹理细节描述能力很强。尽管如此，LBP理论在实际应用中仍然存在诸多问题，主要表现为特征模式过多，对图像几何变化鲁棒性差且忽略了局部纹理之间的相互联系。

针对于特征模式过多的问题，Ojala等提出了统一模式的LBP算法。当P为8时，LBP的特征模式个数由原来的256减少为59，减少了近77%。为了使LBP同时具有旋转不变性，Ojala进一步提出了旋转不变的统一LBP算法，当P为8时，LBP由原来的256种减少为10种，减少了近96%的特征模式。

针对于LBP算法忽略了局部纹理之间的相互联系的问题，徐少平等人提出了ILBP算法，在该方法中纹理特征的描述符不再采用为图像中所有像素点的LBP值建立的直方图的方式实现对图像的刻画，而是从一定角度、偏移距离的相邻LBP值对中提取多个统计值并构成特征矢量的方式实现对图像描述。具体来说，就是先求出原图像每个像素点的LBP，并称所有LBP值构成的图像为伪图像，再在此伪图像的基础上用GLCM算法计算各个二次统计量作为最后的纹理特征。

1.3 DWT算法

与傅里叶变换不同，小波变换是基于一些小型波，称为小波，其具有变化的频率和有限的持续时间［16］。小波变换在进行图像处理时，不仅能反映图像的频谱信息，同时还能反映图像像素的空间信息。多尺度分析是小波变换的1个很重要的应用。

对图像的小波变换就是把图像f（x，y）从空间Vj＋1投影到空间Vj上，即将图像缩小了1个尺度。这样图像将会损失一些信息，若将Vj在Vj＋1上的正交补空间定义为Wj，即

则空间Wj将包含图像f（x，y）从Vj＋1投影到Vj时丢失的所有信息。鉴于此，空间Wj又常称为尺度j上的细节空间。空间j上的图像又可以继续地向下1个尺度投影，即有

式中：j0为任一起始尺度。图像的纹理特征可以用图像在每个分解层上系数的均值和方差表示。

见图2（a），若用sym2对其进行2次2尺度分解，则分解后的图像见图4（b）。其纹理特征就可用14个特征分量表示，这14个分量分别为图2（b）中7幅图像灰度值的均值和方差。

图2 二尺度DWTFig.2 Two-scale DWT

2 基于多特征的纹理特征提取

GLCM算法是统计纹理中某1像素对出现的概率，包含了纹理的整体信息，适用于描述大而疏的纹理；LBP算法是统计纹理各个LBP模式的直方图，纹理细节信息丰富，适用于描述小而密的纹理；DWT算法则能对纹理进行多尺度分析，对图像的尺寸变化不敏感，具有较好的尺度不变性。为了能兼顾各算法的优点，笔者提出了1种基于多特征的纹理特征提取算法，将GLCM算法、LBP算法以及DWT算法提取的特征参数合为一个向量，并以此作为最终的特征向量来描述图像的纹理，其维数是3种算法的维数之和。

设GLCM算法提取的特征向量为

式中：m为GLCM算法提取的特征维数，设旋转不变的统一LBP算法提取的特征向量为

式中：n为旋转不变的统一LBP算法提取的特征维数。设DWT算法提取的特征的特征向量为

则融合GLCM算法、LBP算法和DWT算法的特征向量为

其维数为（m＋n＋t）。

2.1 高斯归一化

由于特征向量的各个特征分量的取值范围以及物理含义不同，在进行图像检索之前还需要对其进行内部归一化。各种归一化中应用最为成熟的是高斯归一化，其特点是少量边界点的值基本不影响归一化后各参数值的分布，本文将采用这种方法［17］。

设图像纹理的N维特征向量为F＝［f1，f2，…，fN］，图像库中的M 幅图像分别表示为I1，I2，…，IM，则图像Ii对应的特征向量就可以记为F＝ ［fi1，fi2，…，fiN］。按这种表示方法就可以将图像库中的M幅图像各自的特征参数表示成1个二维M×N 矩阵F ＝ ｛fi，j｝.其中：fi，j为第i幅图像的第j个特征元素。然后计算每1个特征参数fj的均值μj和标准差δj，再根据式（8）就可以将原特征向量归一化成N（0，1）分布的向量。

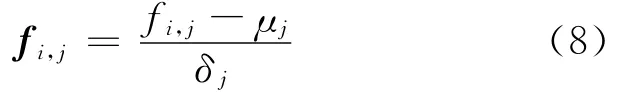
如果在归一化用3δj代替δj进行，则特征参数fi，j的值将以99%的概率落在区间［－1，1］上。在实际应用中，通常可将归一化后大于1的特征值定义为1，并将小于－1的特征值定义为－1，这样就可以保证归一化后所有的特征值都落在区间［－1，1］上。

2.2 相似性度量

在基于内容的图像检索过程中，通常是通过特征的相似性度量来实现对图像特征的匹配。这种相似性度量就是用某种相似性准则计算两幅图像纹理特征之间的距离，然后根据距离的大小判断检索图像和目标图像间的相似程度。相似性度量与特征提取一样，它的合适与否将直接影响着图像检索的效果。

设2幅图像的特征向量分别为x＝（x1，x2，…，xn）与y＝ （y1，y2，…，yn），则常用的相似性度量方法有以下几种［18］。

街区距离。

欧式距离。

LP范数距离。

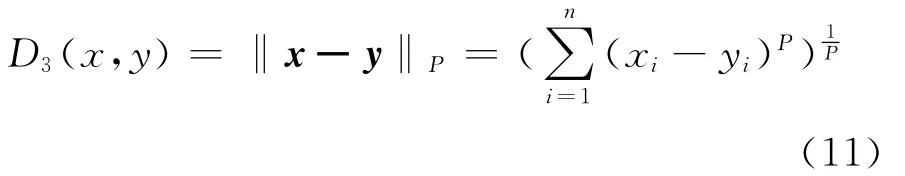
马氏距离。

在这些相似性度量中，马氏距离能够考虑各特征向量的权重，这使得其在有些时候有较强的纹理特征匹配能力，适用于计算自回归纹理特征的相似度，它的不足之处是计算量大。相比而言，LP范数距离的计算量就要小得多，且也具有较高的纹理特征匹配能力。当LP范数距离中的P＝1时，LP范数距离就是街区距离；当P＝2时，就是街区距离。街区距离和欧式距离一般用于纹理特征向量的各个分量正交无关且权重相同的场合，这两种方法计算简单，在相似性度量中被广泛地使用。由于本文的纹理特征向量已经进行了高斯归一化，各个特征分量的权重相同，所以本文的相似性度量选择街区距离和欧式距离

实际应用中，1幅纹理图像或是整体突出，或是细节突出，其尺度变化也不尽相同。若对各分量的贡献不加以区分而统一赋以相同的权重，最后检索的效果难以达到最优。考虑到这一点，本文先分别计算GLCM算法、LBP算法以及DWT算法对应的欧式距离，再进行权重相加。即

式中：D1、D2和D3分别为GLCM算法、LBP算法以及DWT算法对应的欧式距离，w1、w2和w3分别是与之相对应的权重，满足w1＋w2＋w3＝1。

2.3 权重配置

关于权重的配置，可以采用经验调试法。调试的依据是各方法识别纹理的侧重点：GLCM算法侧重于纹理的整体，LBP侧重于纹理的细节，而DWT则侧重于纹理的尺度变化。这种配置方法能够粗略地给出各个权重系数，但其也存在一定的缺陷，如所需调试次数过多，配置的权重系数只能达到局部最优。

调试时采用的权重初值可以根据GLCM，LBP和DWT 3种基本算法单独使用时，检索的精度确定。若单独使用时，GLCM算法检索的精度为p1，LBP算法检索的精度为p2，DWT算法检索的精度为p3，则3种算法的权重年初值可以确定为w1＝p1／（p1＋p2＋p3），w1＝p2／（p1＋p2＋p3），w1＝p1／（p1＋p2＋p3）。

3 图像检索结果与分析

本文的检索图像库采用Corel图像库，该库中有1 000幅图像，分为了10类，其中部分图像见图3。每次检索返回20幅检索图像，并用查准率Pk来反映检索结果的准确性，以比较各算法提取的特征对纹理的描述能力。式（14）为Pk的定义［19］。

图3 Corel图像库中的部分图像Fig.3 Portion of the image in Corel image library

经过调试，在GLCM算法中，选择像素对距离d为1，灰度级L为64，窗口大小M×N为图像的尺寸，此时针对于Corel库的检索的效果最好；同时为了使用和差统计法，特征参数选用角二阶矩、对比度、相关性和熵。在LBP算法中，选用旋转不变的统一LBP算法。在DWT中，采用2阶一维对称小波sym2，并对图像进行3层小波分解。

3.1 Corel库检索实验

在Corel图像库的10类图像中，每1类都随机取10幅图像，分别对这100幅图像采用GLCM算法、LBP算法、DWT算法、ILBP算法以及本文算法（记为G＿L＿D）进行图像检索实验。分别采用欧式距离和街区距离计算每1种算法下检索的平均查准率以及该算法下每1类图像检索的平均查准率，其结果见表2和表3。其中G＿L＿D＿0为未加权时的多特征组合算法；G＿L＿D算法在欧式距离下的权重配置为w1（GLCM）＝0.33，w2（LBP）＝0.55，w3（DWT）＝0.12；在街区距离下的权重配置为w1＝0.56，w2＝0.30，w3＝0.14。

观察表2和表3可知，在街区距离下的各算法的平均查准率几乎都要高于欧式距离下的平均查准率率。尤其是在本文的G＿L＿D算法下，采用街区距离对各类图像检索的查准率都要高于欧式距离下查准率，其平均查准率提高了2%（查准率提高5%表示在检索的20幅图像中能多得到一幅正确的图像），这表明采用街区距离更适用于本算法做图像检索。实际上，与欧式距离相比，街区距离能降低个别较大的特征分量对检索结果的影响，使其他的特征分量的作用能更充分地发挥出来。

表2 Corel库中各算法在欧式距离下的平均查准率Tab.2 Average precision of each method in Corel image library used Euclidean distance

表3 Corel库中各算法在街区距离下的平均查准率Tab.3 Average precision of each method in Corel image library used Cityblock distance

进一步观察表3可知，G＿L＿D算法的平均查准率比GLCM算法高20%、比LBP算法高9%，比DWT算法高10%，比ILBP算法高15%，比G＿L＿D＿0算法高2%。这表明在实际做图像检索过程中，在返回的20幅图像中，本文提出的多特征融合算法能比GLCM算法平均多得到4幅正确图像，比LBP算法和DWT算法多得到2幅正确图像，比ILBP算法多得到3幅正确图像，对图像的检索效果有了明显的改善。需要注意的是，在使用徐少平等人提出的ILBP算法做图像检索实验时，检索效果并不理想，检索的平均查准率介于GLCM算法和LBP算法之间，并远低于本文的G＿L＿D算法。这主要是因为ILBP算法虽然对图像像素空间位置的描述有所改善，但是却丢失了大量的细节信息，在图像检索时容易与其他类的图像混淆，检索效果不佳。通过与G＿L＿D＿0算法检索结果的对比可以发现，在多特征组合时，如果为每1种基本算法赋以1个合适的权重，检索效果将得到进一步的提高。

由表3还可以发现，在检索海滩、恐龙、马匹等纹理大而疏的图像时，GLCM算法的查准率与LBP算法相当；在检索非洲、公汽、美食等纹理细而密的图像时，LBP算法的查准率就要远高于GLCM算法，其中对于非洲类图像提高了29%，对于公汽类图像提高了24%，对于美食类图像提高了28%。这表明GLCM算法对图像整体检索效果较好，LBP算法则更关注于图像的细节，与理论分析相符。

3.2 旋转不变性实验

在前面对3种基本算法的介绍中，GLCM算法、LBP算法以及DWT算法均具有较好的旋转不变性，则基于它们的多特征融合算法也将具有较好的旋转不变性。为验证这一点，本文也做了相应的实验。在该实验中，随机在Corel图像库的10类图像中的每1类中取10幅图像，然后对这100幅图像进行垂直、水平镜像，并依次旋转60°，120°，180°，240°和300°，这样包括处理前图像，共得到了1个包含了800幅图像的库。将该图像库称为Corel＿r库并作为系统的检索库，采用街区距离，计算不同算法下的平均查准率如表4所示。其中G＿L＿D的权重配置为w1＝0.48，w2＝0.27，w3＝0.25。

由表4可见，与表3相比，在图像旋转或镜像后，各算法检索的查准率并没有下降，且普遍高于Corel库的准确率。表明无论是GLCM算法、LBP算法，DWT算法还是本文的多特征融合算法均具有一定的旋转的不变性。同时还可以发现本文的G＿L＿D算法检索的平均查准率仍比GLCM算法高18%，比LBP算法高11%，比DWT算法高出12%，比ILBP算法高出19%，进一步验证了本文算法对纹理特征描述的能力。

表4 Corel＿r库中各算法的平均查准率Tab.4 Average precision of each method in Corel＿r image library

3.3 尺度不变性实验

为了比较各算法的尺度不变性，本文另做了1组实验，取Corel图像库中每类图像10幅，得到100幅图像的基库，然后对这100幅图像分别放缩0.25倍、0.5倍、1.5倍和2倍，这样加上原来的100幅图像，就得到了1个包含500幅图像的库，记为Resize库。以该库为实验对象，采用街区距离，分别计算不同算法下的平均查准率见表5。其中G＿L＿D的权重配置为w1＝0.64，w2＝0.01，w3＝0.35。

表5 Resize库中各算法的平均查准率Tab.5 Average precision of each method in Resize image library

由表5可见，本文的G＿L＿D算法的平均查准率比GLCM算法提高了9%、比LBP算法提高了18%、比DWT算法提高了5%，比ILBP算法提高了10%。表明本文的多特征融合算法也具有较好的尺度不变性。

3.4 计算效率实验

在以上几个实验中，对各算法的纹理描述能力进行了比较。为了更进一步比较各算法的优劣，本文也对各算法的计算效率进行了对比。在该实验中，比较了各算法提取Corel图像库中1 000幅图像所需的时间，实验结果见表6。

表6 各方法提取1 000幅图像所需的时间Tab.6 Time of extracting 1000images by each method

由表6可见，ILBP算法提取Corel中1 000幅图像所需的时间为GLCM算法与LBP算法所需的时间之和；DWT算法所需的时间与GLCM算法，LBP算法以及ILBP相比，要高出1个数量级。而本文提出的G＿L＿D算法提取1 000幅Corel图像所需的时间则为GLCM算法，LBP算法和DWT算法所需的时间之和，约8min。这在实际使用中，尤其是当图像库更大时极为不便。因此在使用本文算法时，其时间消耗必须要加以考虑。

4 结束语

在对纹理图像的特征提取中，GLCM算法侧重纹理的整体信息，LBP算法侧重纹理的细节信息，DWT算法具有较好的尺度不变性，而笔者提出的基于多特征的纹理特征提取算法则能很好地兼顾前面3种算法的优点。通过权重的配置，其可以适用于不同的纹理图像，具有较强的实用性。最后的图像检索实验进一步表明，不仅在纹理描述能力上有了明显的提高，同时还具有较好的旋转不变性和尺度不变性。本文算法的不足之处在于需要同时提取出GLCM算法、LBP算法，以及DWT算法下的纹理特征，计算所需的时间为后3种算法所需时间之和，使算法的实用性受到了一定的限制。本文下一步工作主要有2个方面，一是对GLCM算法，LBP算法以及DWT算法原理做进一步分析，研究各特征分量的内在联系，寻找更简洁有效的融合方法，减少算法的计算量。二是结合图像检索的原理，基于聚类的思想，寻找一种可行性高且适用性强的权重配置方法。

［1］ 黄明晶，刘 清，熊燕帆，等.面向内河雾天图像的大气光亮度值估算方法研究［J］.交通信息与安全，2013，31（3）：33-37.HUANG Mingjing，LIU qing，XIONG Yanfan，et al.Atmospheric light estimating algorithm based on inland haze image［J］.Journal of Transportation Information and Safety.2013，31（3）：33-37.（in Chinese）

［2］ HARALICK R M，SHANMUGNM K，DINSTEIN I.Textural features for mageclassification［J］.IEEE Transactions on Systems，Man.And Cybernetics，1973，3（6）：610-621.

［3］ CHEHAPPA R，CHATTERJEE S.Classification of texture using ganssian markov random fields［J］.IEEE Transactions OH Acoustics，Speech.and Signal Processing，1985，33（4）：959-963.

［4］ MALLAT S G.A theory for multiresolution signal decomposition：the wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11（7）：674-693.

［5］ OJALA T，PIETIKAINEN M，MAENPAA T.Multiresolution gray-scale and rotation Invariant texture analysis with local binary patterns［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24（7）：971-987.

［6］ 刘丽，匡纲要.图像纹理特征提取方法综述［J］.中国图象图形学报，2009，14（4）：622-635.LIU Li，KUANG Gangyao.Overview of image textural feature extraction methods［J］.Journal of Image and Graphics，2009，14（4）：622-635.（in Chinese）

［7］ CLAUSI D A.DENG H.Design-based texture feature fusion using gabor filters and co-occurrence probabilities［J］.IEEE Transactions on Image Processing，2005，14（7）：925-936.

［8］ ACQUA F D，GAMBA P.TRIANNI G.Semi-automatic choice of scaledependent features for satellite SAR image classification［J］.Pattern Recognition Letters，2006，27（4）：244-251.

［9］ 薄 华，马缚龙，焦李成.图像纹理的灰度共生矩阵计算问题的分析［J］.电子学报，2006（1）：155-158.BO Hua，MA Fulong，JIAO licheng.Research on computation of GLCM of image texture［J］.Acta Electronica Sinica，2006，34（1）：155-158.（in Chinese）

［10］ 徐少平，刘小平，李春泉，等.基于LBP值对空间统计特征的纹理描述符［J］.模式识别与人工智能，2013（8）：769-776.XU Shaoping，LIU Xiaoping，LI Chunquan，et al.Texture descriptor based on spatial statistical features of local binary pattern code pair［J］.PR＆AL，2013（8）：769-776.（in Chinese）

［11］ 黄 晶.基于分形维度与灰度共生矩阵的图像分类研究［D］.武汉：武汉理工大学，2008.HUANG Jing.Image classification based on the fractal dimension and GLCM［D］.Wuhan：Wuhan University of Technology，2008.（in Chinese）

［12］ UNSER M.Sum and difference histograms for texture classification［J］.IEEE Transation on Pattern Analysis and Machine Intelligence，1986，8（1）：118-125.

［13］ 苑丽红，付 丽，杨 勇，等.灰度共生矩阵提取纹理特征的实验结果分析［J］.计算机应用，2009，29（4）：1018-1021.YUAN Lihong，FU Li，YANG Yong，et al.Analysis of texture feature extracted by gray level co-occurrence matrix［J］.Journal of Computer Applications，2009，29（4）：1018-1021.（in Chinese）

［14］ 宋克臣，颜云辉，陈文辉，等.局部二值模式方法研究与展望［J］.自动化学报，2013，39（6）：730-744.SONG Kechen，YAN Yunhui，CHEN Wenhui，et al.Research and perspective on local binary pattern［J］.Acta Automatica Sinica，2013，39（6）：730-744.（in Chinese）

［15］ 李 丹.局部二进制模式的理论和应用问题研究［D］.天津：天津理工大学，2011.LI Dan.Research of theory and application on local binary pattern［D］.Tianjin：Tianjin University of Technology，2011.（in Chinese）

［16］ RAFAEL C.GONZALEZ，RICHARD E.woods.数字图像处理［M］.阮秋琦，阮宇智，译.北京：电子工业出版社，2007：288-312 Rafael C.Gonzalez，Richard E.woods.Digital Image Processing［M］.Translated by：YUAN Qiuqi，Yuan Yuzhi.Beijing：Publishing House of Electronics Industry，2007：288-312.（in Chinese）

［17］ 安志勇，赵 珊，周丽华.基于形状和纹理的图像检索［J］.计算机科学，2006，33（11）：225-232.AN Zhiyong，ZHAO Shan，ZHOU Lihua.Shapetexture based image retrieval［J］.Computer Science，2006，33（11）：225-232.（in Chinese）

［18］ 杨秀娟.基于纹理特征的图像检索研究［D］.西安：西安科技大学，2009.YANG Xiujuan.Research of image retrieval based on texture［D］.Xi＇an：Xi＇an University of Science and Technology，2009.（in Chinese）

［19］ 张松林.基于纹理特征的图像检索方法研究［D］.重庆：重庆大学，2010.ZHANG Songlin.Research of image retrieval based on texture［D］.Chongqing：Chongqing University，2010.（in Chinese）