公交联动发车模型的研究
陈利霖 李珣辉 邹智军▲
(1.同济大学道路与交通工程教育部重点实验室 上海201804;2.新疆交通职业技术学院 乌鲁木齐831401)
0 引 言
公共交通在居民的出行中扮演着越来越重要的角色,如何降低乘客的候车时间是交通相关学者及公交运营者关注的课题。乘客的候车时间可以分为2部分:在出发站O的等待时间Wo及在换乘站点的换乘时间Wt,见图1。
目前普遍存在的问题是一些乘客前往目的地有多条公交路线可供选乘,但是那几路公交车却总是同时到站,使得Wo的值居高不下;而对于一些换乘乘客而言,换乘车辆到站时刻与其到站时刻总是不同步,这也就使得Wt的值偏大。
为了降低乘客的候车时间,国内外交通相关学者进行了不少研究。何迪等[1]综合考虑公交内部线路间的换乘衔接,以乘客在区域内的总换乘时间最小为优化目标,建立区域协同发车时刻表
1 联动发车需满足的条件
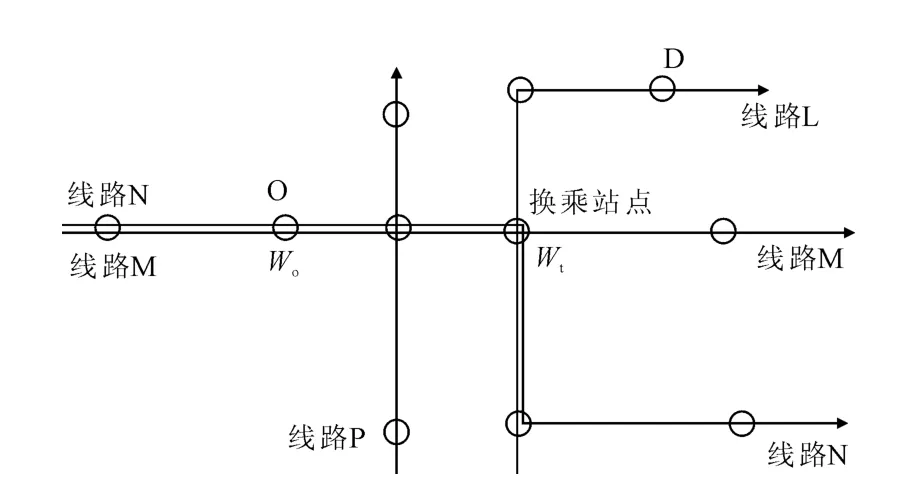
图1 乘客候车时间分类Fig.1 Classification of passengers'waiting time
模型。戴连贵等[2]根据客流变化规律,对发车间隔采用分时段多目标组合优化处理的思想,建立了以乘客候车时间和公交企业运营费用最小为目标的公交车辆调度发车间隔模型。VOSS[3]把最小化乘客在换乘点等待时间的问题表示为Lawler和Hillier等描述的二次分配问题。林叶倩[4]
将可变线路式公交调度模型描述为混合整数规划问题,以公交公司运营成本和乘客出行费用总和最低为目标建立可变线路式公交调度模型。Fabian Cevallos等[5]以换乘时间最短为目标函数,采用遗传算法随机地安排公交的到达。刘芹[6]建立了以企业受益和乘客利益最大为目标的公交调度模型,采用差分进化细菌觅食算法对模型进行了求解。李发智等[7]在建立公交发车间隔模型时,综合考虑了乘客时间成本和车辆的载客率。王建等[8]建立了在冰雪条件下基于乘客等待费用最小化、公交线路效益最大化的发车间隔优化模型。但是,文献[1,3,5]只考虑了降低Wt的值,却未考虑降低Wo的值;文献[2,4,6-7]在兼顾企业和乘客利益的条件下,通过适当调整各线路的发车间隔来降低乘客的候车时间;文献[8]只考虑了单线路的情况。以上的相关研究都无法在维持公交运营成本不变(即不改变原有公交路线的发车时间间隔)的前提下,仅通过调整各路线的发车时刻,来降低所有乘客的总候车时间,即Wt与Wo之和。
本文在借鉴信号交叉口联动控制的基础上,提出公交联动发车需满足的条件,建立了公交联动发车模型。以联动发车系统中乘客的总候车时间最少为目标函数,在维持公交发车间隔不变的前提下,仅通过调整各线路的发车时刻来获得目标函数的最优解。采用遗传算法对模型进行了求解,最后采用实例对模型的有效性进行了验证:对比了采用联动发车模型与仅考虑换乘的发车模型(目前主流的区域协同发车模型)的乘客总的候车时间。
城市道路信号交叉口通过联动控制可以降低车辆的延误[9],若对城市公交路线进行联动发车也可以降低乘客的候车时间。但不是所有的交叉口都适合信号联动控制,同样也不是所有的公交路线都适合联动发车的。联动发车路线需满足以下条件。
1.1 发车时间间隔
对于发车时间间隔相同(或者是倍数关系)的公交路线而言,当首趟车发车时刻确定后,其相互之间的发车时刻差是稳定不变的。故通过调整首趟车的发车时刻,就可以使得各路线公交到达某一站点的时刻差是稳定的,各路线之间稳定的到站时刻差是联动发车的基础。
1.2 换乘联系
对于有站点重合的公交线路,相互之间存在着直接的换乘联系(如图1中的线路L,M,N),可考虑将其纳入联动发车系统。而对于没有1个站点重合的2条公交路线,相互之间没有直接的换乘联系,但可能有间接的换乘联系(即2次以上的换乘联系),其可以分解成几个直接的换乘联系(如图1中的线路P,L可分解成从线路P换乘到线路M或N及从线路M或N换乘到线路L),这时也可以考虑将这2条公交路线路纳入联动发车系统。
2 确定乘客的候车时间
假设:
1)不考虑道路运行条件的影响。
2)若乘客认定某一出行方案成本高于其他出行方案成本,或者倾向于选择其他出行方案,则认定该出行方案对于该乘客无效。
3)为了便于分析,将同1条路线的上下行看作是2条不同的路线。
2.1 乘客的分类
在同一站点,不同乘客的特性可能有所不同,同时其可选择的路线也有所不同。若乘客有多条公交路线可供选乘,则称该乘客为弹性乘客;若乘客只有惟一路线可供选择,则称该乘客为刚性乘客。详细的乘客特性分类见图2。
2.2 站点S所有乘客的候车时间
设联动发车系统中线路i的发车间隔为Ti,其首趟车的发车时刻为t′i,令

式中:tLi为路线i的全程运行时间;NN为联动发车系统中的公交路线数。

图2 乘客特性分类Fig.2 Classification of passengers'characteristic
为了统计到各路线各站点客流的到达及换乘情况,以t为开始统计乘客候车时间的时刻,以T为统计时间段。在统计时间段内,第i路公交累计到站S(站点S为线路i的任意1个站点)的辆数为

根据站间距、停站时间及公交车辆的运行速度可推算出在统计时间段T内路线i到达站点S的第1趟车的时刻,则其第x(x≤Ni)趟车到达站点S的时刻为

在站点S,设有n路公交车停靠,若某1乘客为ETP或EOP,则将其可选择的路线组合定义为路线集合S,设站点S不同的路线集合ΩSk的数量为m;该站点的候车时间Wt以WtS表示,候车时间Wo以表示。
1)STP乘客的候车时间。若第i路第x趟公交车在站点S有个乘客换乘第j路公交,则这个乘客总的换乘时间为


则在站点S,所有STP乘客的候车总时间为

2)ETP乘客的候车时间。若第i路第x趟公交车在站点S有个乘客换乘路线集合,则这个乘客总的换乘时间为
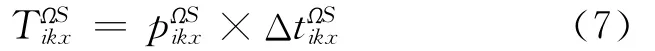


则在站点S,所有ETP乘客的候车总时间为
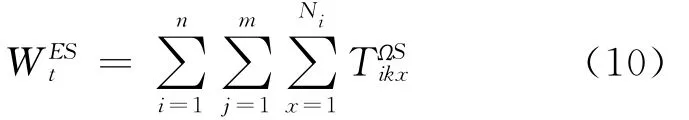
可得

设站点S的OP乘客到达率为fS(x),其中SOP乘客所占的比率为,则EOP乘客所占的比率为1-。
1)SOP乘客的候车时间。设SOP乘客中选乘第i路公交的比率为,则所有选乘第i路公交的SOP乘客的候车时间为
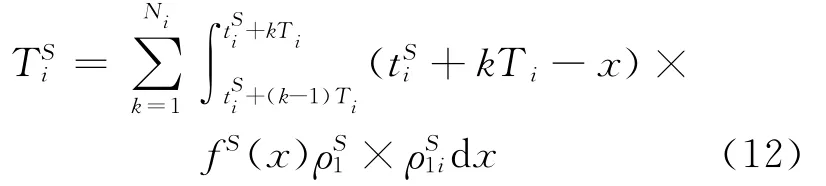
则在站点S所有SOP乘客的候车总时间为


则在站点S所有EOP乘客的候车总时间为

可得
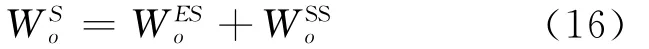
在统计时间T内,站点S所有乘客的候车时间为

2.3 联动发车系统中所有乘客的总候车时间
所有乘客总候车时间为W =∑WS,但其中必须满足的约束条件为
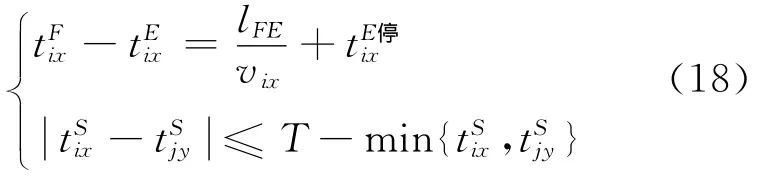
式中:tFix,tEix分别为第i路第x趟公交车到达相邻站点F、E的时刻;lEF为相邻站点E、F之间的距离;vix为第i路第x趟公交车在站点F、E之间的运行速度;tE停ix为第i路第x趟公交车在站点E的停靠时间。
3 模型的求解
联动发车模型的目标函数为minW=∑WS。要求得该目标函数的最优解,即在式(18)的约束下,搜寻各路公交最优的发车时刻opt(t′i)。由于目标函数为NN (对于大城市来说,可能NN的值能达到几十甚至上百)元多次非线性函数,若采用传统迭代搜索方法容易陷入局部最优解,若将其看成是整数规划问题采用枚举法进行逐一比较,运算次数将达到Ti次,效率极其低下;而作为智能算法的遗传算法不存在该问题,适合作为该模型的求解方法[10-11]。该模型采用遗传算法求解的流程如下。
步骤1 输入站点特性、换乘特性、线路的发车间隔等参数信息。对各路公交的发车时刻t′i进行编码,给出1个有NN 个染色体的初始种群pop(tt),tt=1。
步骤2 对pop(tt)中的每1个染色体pop(tt)i计算它的适应值,由于公交联动发车模型的目标函数为所有乘客的总候车时间最小,故将适应值计算函数设计成

式中:Wmin为同1代种群中最佳个体的目标函数值,Wpop(tt)i为染色体pop (tt)i的目标函数值。
步骤3 判断种群的进化代数tt是否满足设置的最大进化代数TT,若满足,则算法停止,输出结果;否则,计算概率

并依此概率分布从pop(tt)中随机地选NN个染色体构成1个新种群newpop(tt+1)。
步骤4 选定杂交概率为pc(该值一般选择80%~95%),通过杂交,得到1个有NN 个染色体的crosspop(tt+1)。
步骤5 以1个较小的概率pm(该值一般选择0.5%~1%),使得1个染色体的1个基因发生变异,形成mutpop(tt+1)。
步骤6 令tt=tt+1,pop()tt=mutpop(tt),返回到步骤2。
4 案例分析
已知上海市曹安公路上某一区段的公交线网如图3所示,网络中有6条线路,6个站点。由于该区段为郊区公路,非高峰时段交通流量不大,假定同一站点间公交车辆运行时间相同;由于该公交线网为郊区线路,客流量不大,假定每辆车在每个站点的停靠时间都相同为1min。其中2车站间的数字为路段行车时间、括号内的数字为各路公交的发车间隔。
根据公交联动发车系统应满足的条件,筛选出北安线、陆安专线、嘉松线、安亭5路这4条公交线路将其纳入到公交联动发车系统中,其中乘客候车时间的统计时段选择为30min。站点特性和换乘特性见表1和表2。

图3 公交网络Fig.3 Bus network

表1 站点特性Tab.1 Characteristics of bus stops
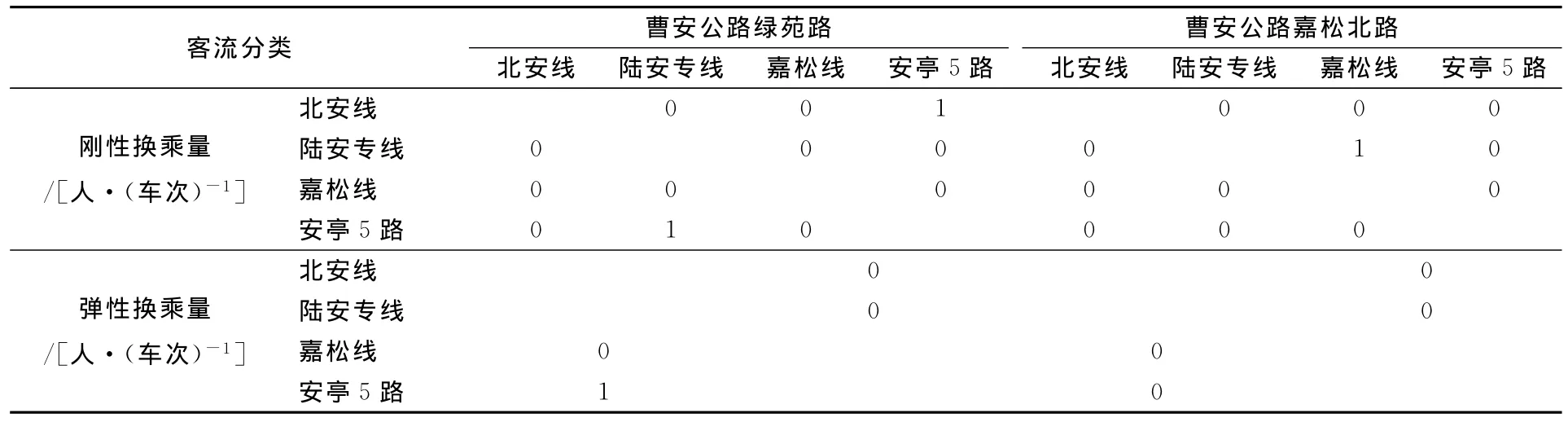
表2 换乘特性Tab.2 Transfer characteristics
分别计算采用联动发车模型以及采用区域协调调度优化模型(目前较主流的发车模型:以公交车辆在枢纽站点相遇次数最多为目标函数)[12-13]情况下,乘客的总候车时间。
1)联动发车。将表1与表2的数据代入联动发车模型,采用遗传算法对案例进行求解,详细的求解过程可采用数学软件Matlab中的工具箱来进行[14],本案例采用的计算参数为种群数=50,进化代数=200,初始交叉概率=0.85,初始变异概率=0.05。最终的求解结果为:当陆安专线与嘉松线同步到达曹安路绿苑路站,安亭5路与北安线同步到达曹安公路绿苑路站,陆安专线与北安线到达曹安公路绿苑路站的时刻差为7.5min时,乘客总的候车时间最小为:845.5人·min。
2)区域协调调度.由于该线网路线较少,可以直接看出在统计时段内北安线、陆安专线、嘉松线、安亭5路第一趟车同时到达曹安公路绿苑路站时,公交车辆的相遇次数最多(换乘时间最少)。最终求解结果为:乘客的总候车时间为997.5人·min。2种发车条件下,乘客总候车时间对比见表3。

表3 2种发车条件下总候车时间比较Tab.3 Comparison of the total waiting time in two different cases
由表3可见,联动发车条件下乘客总的候车时间较区域协调调度降低了15.2%。由此可知,联动发车模型较区域协调调度模型在降低乘客总的候车时间方面更具优势,特别是在公交线路重复度系数较高的区域即乘客出行可供选择的路线较多的区域,但必须满足的条件是,在该区域公交线路的发车时间间隔成倍数关系。
5 结束语
笔者列出了公交车进行联动发车必须满足的条件,建立了区域公交车联动发车模型,并且通过实例计算验证了联动发车在降低乘客总候车时间方面的效果。联动发车不需要调整各公交路线的发车时间间隔,只是通过调整各路公交车首班车的发车时刻来降低乘客的平均候车时间。该发车模型不仅考虑到了Wo,还考虑了Wt,较一般的区域协同发车模型在降低乘客候车时间方面更有优势。联动发车模型在公交路线重复系数较高的区域有较好的运用前景,特别是设有公交专用道或BRT专用道的城市中心区。
虽然笔者较详细地描述了整个模型的构造过程,但是对于公交车辆在站点的停靠时间、特别是停靠时间与上下车乘客的数量关系有待进一步考虑。
[1] 何 迪,严余松,户佐安,等.基于区域协同的公交发车时刻表模型[J].计算机应用研究,2009(4):1282-1285.HE Di,YAN Yusong,HU Zuoan,et al.Model of bus dispatching timetable base on regional collaboration[J].Application Research of Computers,2009(4):1282-1285.(in Chinese).
[2] 戴连贵,刘正东.公交调度发车间隔多目标组合优化模型[J].交通运输系统工程与信息,2007(4):43-46.DAI Liangui,LIU Zhengdong.Research on the multi-objective assembled optimal model of departing interval on bus dispatch[J].Journal of Transportation Systems Engineering and Information Technology,2007(4):43-46.(in Chinese)
[3] VOSS S.Network design formulation in schedule synchronization[M].Berlin:Computer-Aided Transit Scheduling,1992:137-152
[4] 王森磊,马继辉.基于遗传算法的公交车辆数优化[J].交通信息与安全,2013(5):45-50.WANG Senlei,MA Jihui.Optimization of a Bus Scheduling Model Based on Genetic Algorithm[J].Journal of Transportat Information and Safety,2013(5):45-50.(in Chinese)
[5] FABIAN Cevallos,FANG Zhao.A genetic algorithm for bus schedule synchronization[C].Proceedings of the Ninth International Conference on Applications of Advanced Technology in Transportation,Chicago,USA:American Society of Civil Engineers,2006.
[6] 刘 芹.差分进化细菌觅食算法求解公交车调度问题[J].交通运输系统工程与信息,2012(2):156-160.LIU Qin.Differential evolution bacteria foraging optimization algorithm for scheduling problem[J].Journal of Transportation Systems Engineering and Information Technology,2012(2):156-160.(in Chinese).
[7] 李发智,肖 蕾,杨东援.公交发车间隔模型研究[J].武汉理工大学学报:交通科学与工程版,2013(1):92-96.LI Fazhi,XIAO Lei,YANG Dongyuan.Optimal departure timetables for bus line[J].Journal of Wuhan University of Technology:Transportation Science &Engineering Edition,2013(1):92-96.(in Chinese)
[8] 王 建,何建平,洪麟琳.冰雪条件下公交发车间隔优化研究[J].武汉理工大学学报:交通科学与工程版,2013(2):254-257.WANG Jian,HE Jianping,HONG Linlin.Optimization of bus dispatching interval under the condition of Ice and snow[J].Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2013(2):254-257.(in Chinese)
[9] 吴 兵,李 晔.交通管理与控制[M].北京:人民交通出版社,2010:122-130.WU Bing,LI Ye.Traffic management and control[M].Beijing:China Communication Press,2010:122-130.(in Chinese)
[10] 梁艳春,吴春国,时小虎,等.群智能优化算法理论与应用[M].北京:科学出版社,2009:34-42.LIANG Yanchun,WU Chunguo,SHI Xiaohu,et al.Theory and application on swarm intelligence optimization algorithm[M].Beijing:Science Press,2009:34-42.(in Chinese)
[11] WANG Qingrong,ZHU Changsheng.Improved genetic-tabu search algorithm in bus scheduling study[C].2010 3rd International Conference on Computer and Electrical Engineering (ICCEE 2010).Singapore:IACSIT Press,2010:87-93
[12] CEDER A.Bus timetables with even passenger loads as opposed to even headways[J].Transportation Research Record:Part B,2002(17):26-39.
[13] 田启华,陈艳艳.区域公交协调调度优化算法研究[J].交通运输系统工程与信息,2011(4):160-165.TIAN Qihua,CHEN Yanyan.Coordinated scheduling optimization for public transport hub[J].Journal of Transportation Systems Engineering and Information Technology,2011(4):160-165.(in Chinese)
[14] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005:223-247.LEI Yingjie,ZHANG Shanwen,LI Xuwu,et al.Genetic algorithm toolbox of MATLAB and its application[M].Xi’an:Xidian University Press,2005:223-247.(in Chinese)

