基于状态空间的连续断面船舶交通流量预测研究＊

吴 康 汪 洋 谢 磊 吴 兵

（武汉理工大学智能交通系统研究中心 武汉430063）

0 引 言

随着我国航运业的快速发展，各水路航道船舶交通流量迅速增加。长江经济带国家战略的提出、水路运输的快速发展，以及交通事故频发，对各水道规划设计和通航管理提出了更高的要求。船舶交通流量预测是航道设计、规划和管理的基本依据。长江航线武汉段水运繁忙，其突出特点是桥区较多，具有明显的连桥区特征，对其船舶流量进行合理预测具有重要意义。20世纪60年代开始，有学者开始将其他领域已经成熟的预测方法应用于交通流量预测，提出并改进了很多预测方法，可大致分为定性预测方法和定量预测方法。定性预测是指经验判断性质的分析预测，主要依靠专家判断、逻辑推理、经验分析来进行。国内外比较流行的经验分析方法有“Delphi”法［1］。

常用的定量预测方法有回归分析、灰色理论预测神经网络预测、支持向量机以及组合预测方法等。业界对各种方法都有不同程度的研究。张杏谷［2］等利用回归分析法对厦门港2000年货物吞吐量进行预测，并在此基础上预测所需的VTS规模；徐杏等［3］采用BP神经网络对深圳港2000～2005年港口吞吐量进行预测，并表明神经网络预测具有很强的学习和泛化能力；冯宏祥等［4］提出了基于支持向量机理论的船舶交通流量预测模型，并对长江苏通大桥船舶流量进行了有效的预测。除了这些典型的预测方法，有时候会把几种预测方法组合在一起进行组合预测，其基本原理是赋予每种方法不同的权重，充分发挥每种方法的优点。刘敬贤等［5］提出了基于多元线性回归和灰色系统模型的改进CSFM模型，对天津港船舶交通流进行了有效预测。组合预测模型各种方法的组合方式对预测结果影响较大，因此其实用性还需要更多的研究支持。

目前的船舶交通流预测方法多是对单一断面船舶交通流进行预测，而在多点综合预测方面还有很大的研究空间。实际上，从时间序列的角度而言，1个断面的交通状态不仅受自身过去时段交通状态影响，也会受相邻断面的过去时段交通状态影响；因此，笔者基于状态空间建模和卡尔曼滤波算法，将单点船舶流量预测推广到多点同时预测，提出了基于状态空间模型的多断面船舶交通流量预测方法，并对不同时间维度（小时、月份）上的长江武汉段和重庆段连续断面船舶流量进行实证研究。

1 相关研究工作

1.1 时间序列

时间序列是指将某种现象某1个统计指标在不同时间节点上的各个数值按时序排列而形成的序列。如股票的市盈率、月降水量、电力负荷、网络流量等，都形成了1个时间序列［6］。

从时序的角度分析，每个数据单元都可以被抽象为1个二元数组（t，o）。其中：t为时间变量；o为反应数据单元实际意义的数据变量。由此可对时间序列进行如下定义：时间序列是1个有限集｛（t1，o1），（t2，o2），…，（tn，on）｝。其中：ti＜ti＋1，i＝1，2，…，n－1。

时间序列分析不仅可以从数量上揭示某一现象的发展变化规律或从动态的角度刻画某一现象与其他现象之间的内在数量关系及其变化规律性，达到认识客观世界之目的，而且运用时间序列模型还可以预测和控制现象的未来行为。时间序列法是1种定量预测方法，亦称简单外延方法。在统计学中作为1种常用的预测手段被广泛应用。常用的时间序列模型有自回归（AR）模型、移动平均（MA）模型、自回归移动平均（ARMA）模型等，其中自回归模型和移动平均模型都是自回归移动平均模型的特例。

1.2 状态空间法

状态空间法是建立在状态变量描述基础上的对控制系统分析和综合的方法，是现代控制理论的主要内容之一。状态空间法能揭露系统外部变量和内部变量间的关系。由于状态空间具有很好的能控性和能观测性，通过状态空间法可以挖掘出系统的很多潜在特征，状态空间建模为许多实际问题的处理提出了一致的分析框架。将状态空间法用于分析时间序列问题，便于用迭代算法解决时间序列中复杂的参数估计问题，并运用卡尔曼滤波算法进行预测。张世英等［7］提出了1种基于参数拟合的时间序列状态空间模型，并成功应用于预测天津市大气悬浮微粒含量。

状态空间法本质上是1种既能表达系统的外部特性，又能揭示了系统内部状态和性能的时域分析方法，其数学形式就是系统的状态方程。能完整、确切的描述系统时域行为的最小的1组变量称为状态变量，由状态变量组成的向量称为状态向量。而输入向量就是由外接施加并作用于系统的输入变量组成的向量，系统在输入作用下的响应组成的向量称为观测向量。输入向量与观测向量之间的关系由系统观测方程来表示。

1.3 卡尔曼滤波

滤波是指从带有干扰的信号中得到有用信号的准确估计值。卡尔曼滤波是以最小均方误差为估计的最佳准则的递推算法。其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现在时刻的观察值来更新对状态变量的估计，并求出下一时刻的估计值。卡尔曼滤波的实质是由量测值重构系统的状态向量，其递推顺序为“预测－实测－修正”，其 目的是根据系统的量测值消除随机干扰，或根据系统的量测值从被污染的系统中回复系统原本规律。由于卡尔曼滤波采用递推计算，因此非常适宜于用计算机来实现，在交通、金融、航空等领域应用非常广泛。在交通领域，杨兆升、朱中［8］提出了基于卡尔曼滤波理论的交通流量实时预测模型，并提出了2点改进意见，得出卡尔曼滤波算法具有更高精度、适用于整个交通网络进行实时预测的结论；李嘉、刘小兰［9］基于卡尔曼滤波算法建立了道路交通行程时间的确定方法，并说明其具有良好的预测精度。

2 建立模型

建立基于状态空间的多断面船舶交通流预测模型时，首先根据时间序列分析，转化并得到多断面船舶交通流的状态空间方程，最后卡尔曼滤波预测得到下一时刻的流量值。建模的基本流程见图1。

图1 建模基本流程示意图Fig.1 Basic flowchart

2.1 建立交通流状态状态空间模型

假设对n个断面的船舶交通流同时进行预测，则有n维时间序列Qt。

式中：q1t为i个断面t时刻的船舶流量。

根据时间序列Qt建立多维自回归模型，确定回溯系数p后，得到：

式中：A1～Ap为n×n维系数矩阵；ut为零均值白噪声序列。

得到多维自回归模型后，进行适当的数学变换，可将时间序列模型转化为状态空间模型。

式中：yt为系统的观测向量；xt为np维状态向量。于是式（2）表示的时间序列模型可转化为如下状态空间模型。

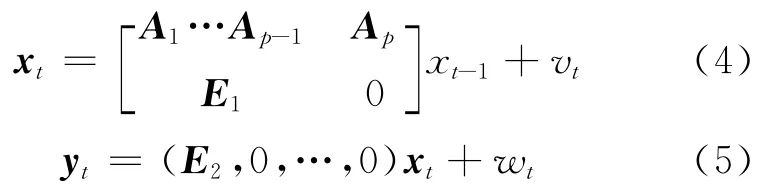
上面2个方程分别为系统状态方程和系统观测方程，设Ft和Ht分别为状态转移矩阵和观测矩阵。则由式（4），（5）有

vt为t时刻的白噪声，均值为0，方差矩阵Gt＝E），wt为观测噪声，其方差矩阵Rt＝E（wt，），E1为n（p－1）维单位矩阵，E2为n维单位矩阵。

2.2 卡尔曼滤波过程

对已经建立的状态空间模型，利用卡尔曼滤波算法进行预测。交通流量状态的预测过程就是根据前一时间的状态向量滤波值进行单步预测。得出现时段的预测结果，然后补充新的数据，对系统状态向量进行更新，计算出当前时刻状态向量滤波值，下1次预测将在此基础上进行循环和递推。卡尔曼滤波过程可用Matlab编程实现。

卡尔曼滤波算法的基本步骤为：

1）确定系数矩阵，状态初始值x0，初始方差矩阵V0。实际上很难直接得到系统初始状态和初始方差分布，但是可以由近似算法得到近似值，然后迭代确定状态初始值x0和初始方差矩阵V0。

2）递推计算过程。

式中：Xt－1｜t－1为t－1时刻系统状态滤波值；Xt｜t－1为根据t－1时刻系统状态滤波值预测得到的滤波向量；Vt－1｜t－1为t－1时刻的系统状态方差矩阵；Vt｜t－1为根据t－1时刻状态方差矩阵预测得到的系统状态方差矩阵。3）滤波过程。

式中：Kt为卡尔曼增益矩阵；Xt｜t为t时刻的系统状态滤波值；Vt｜t为t时段系统状态方差矩阵修正值。

4）输出滤波后的结果。设yt＋1为t＋1时段的多点交通状态n维预测向量，则有

5）重复步骤2），直到预测结束。

3 实例分析

为了检验上述模型的适用性，以2014年4月8日～4月10日长江流域武汉段武汉长江大桥和武汉长江二桥2个断面09：00～16：00时每小时船舶流量（艘次）为研究对象，其中船舶流量指通过此断面的上行流量和下行流量，数据通过长江AIS船舶信息监控系统采集取得。计算过程以4月8日、9日数据为基础，预测10日各断面的交通流量。信息采集界面见图2。

图2 长江AIS船舶信息监控系统Fig.2 The AIS monitoring system of Yangtze river

通过AIS信息监控系统，得到的船舶流量统计数据见表1。

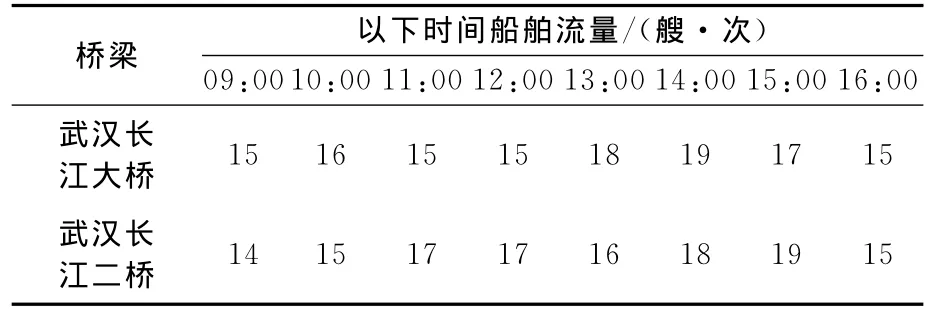
表1 4月8日、9日平均船舶流量Tab.1 The average vessel traffic flow of April 8th and 9th

以4月8日、9日平均船舶流量为预测的基础，确定回溯系数为p＝2，则有多维自回归模型。

式中：t＝1，2，…，8；Q1＝ （15，14）T；Q2＝ （16，15）T；…，A1、A2为2×2维自回归系数矩阵，由多维线性回归得到，由此确定状态转移矩阵Ft。将时间序列模型转化为如下状态空间模型。

由8日、9日交通流数据，经过卡尔曼滤波递推，最终得到的方差矩阵Vt、系数矩阵Ft作为10日数据预测的初始值，运用到交通流量的预测中，得出基于卡尔曼滤波的状态空间预测值。由于初始状态x0，V0并不是1个确定的实际观测值，在适用状态空间模型时为减小初始误差，采用观测数据的平均值作为系统的初始状态值。

为了进行对比，还对测得的数据进行时间序列分析并得到预测结果，2种预测方法得到的Matlab仿真结果见图3、图4。

图3 武汉长江大桥船舶交通流预测结果Fig.3 The forecast results of the Wuhan Yangtze Bridge

图4 武汉长江二桥船舶交通流预测结果Fig.4 The forecast results of the Second Wuhan Yangtze Bridge

由图3、图4可见，使用状态空间模型能够更好地拟合实际船舶交通流。虽然在某些时刻时间序列模型的预测误差较小，但从整体来看，状态空间模型误差预测效果更佳。

为了对预测结果进行对比量化分析，以平均绝对误差（预测值与观测值误差平均值的均值（单位：艘／h）和平均相对误差（预测值与实际值偏差情况）作为对比指标，见表2。

表2 2种预测方法对比Tab.2 Comparison of different forecasting methods

由表2可见，状态空间模型2个桥梁断面平均绝对误差均小于时间序列法预测得到的平均绝对误差，2个断面的平均绝对误差分别减少0.63，0.99；状态空间模型的平均较小，且相对误差处于可接受的范围内，2个断面的平均相对误差分别减少4.59%，0.97%。因此，在预测多断面短时船舶交通流时，基于状态空间和卡尔曼滤波的预测模型是可行的，而且预测结果较时间序列更佳。

为验证状态空间预测模型在不同时间维度上的适用性，同时选取长江重庆段主要观测站（朝天门、万州、巫山）观测船舶流量作为研究对象。将2013年1～9月按月统计的流量数据作为预测的数据基础，建立状态空间模型并通过卡尔曼滤波递推，得到基于状态空间的2013年10～12月份船舶流量预测值；同样作为对比研究，使用回溯系数p＝2的自回归模型，得出在简单时间序列模型下的船舶流量预测值。2种预测方法的预测结果与实际值得对比见表3。

表3 预测值与实际值对比Tab.3 Comparison of the predicted value and the actual value艘／月

对表3数据进行误差分析，得出2种预测方法的平均绝对误差和平均相对误差见表4。从计算结果可以看出，朝天门、万州和巫山3个连续观测点采用状态空间法预测比使用时间序列预测平均绝对误差和平均相对误差均有不同程度的降低，其中平均相对误差分别降低1.08%，4.28%，3.54%。实验结果表明，在以月为单位的时间维度的连续断面船舶流量预测中，状态空间预测模型同样适用。

表4 2种方法误差比较Tab.4 Error comparison of different forecasting methods

4 结束语

船舶交通流量预测是航道规划设计以及航道智能化的重要内容。船舶流量预测的基础是航道上船舶的历史数据，目前常用的数据采集手段有VTS，AIS等。目前对于船舶流量的预测方法大都集中在单一断面的预测，而实际上在研究交通流时，相邻断面的流量是相互作用相互影响的。笔者基于连续断面船舶流量分析，提出了船舶交通流的状态空间模型，并对其进行卡尔曼滤波预测。分析结果表明，多断面预测较单断面预测效果更好，并且模型一旦建立，无需多次建模，预测效率更高。

［1］ 杨 翔.船舶交通流量预测方法研究［D］.大连：大连海事大学，2006.YANG Xiang.Research on vessel traffic volume forecasting［D］.Dalian：Dalian Maritime University，2006.（in Chinese）

［2］ 张杏谷，黄荣坦.2000年厦门港货物吞吐量预测［J］.运筹与管理，1996，5（4）：45-48.ZHANG Xinggu，HUANG Rongtan.The volume forecast of freight handled at xiamen port in 2000［J］.Operations Research and Management Science，1996，5（4）：45-48.（in Chinese）

［3］ 徐 杏，史喜军.深圳港基于BP神经网络的集装箱预测模型［J］.河海大学学报：自然科学版，2002，30（4）：41-44.XU Xing，SHI Xijun.BP neural network-based container throughput predicting model for shenzhen port［J］.Journal of Hohai University：Natural Sciences Edition，2002，30（4）：41-44.（in Chinese）

［4］ 冯宏祥，肖英杰，孔凡邨.基于支持向量机的船舶交通流量预测模型［J］.中国航海，2012（4）：62-66.FENG Hongxiang，XIAO Yingjie，KONG Fancun.Study of vessel traffic forecasting model based on support vector machine［J］.Navigation of China，2012（4）：62-66.（in Chinese）

［5］ 刘敬贤，张 涛，刘 文.船舶交通流组合预测方法研究［J］.中国航海，2009（3）：80-84.LIU Jingxian，ZHANG Tao，LIU Wen.Research on combination forecasting model for ship traffic flow［J］.Navigation of China，2009（3）：80-84.（in Chinese）

［6］ 汤 岩.时间序列分析的研究与应用［D］.长春：东北农业大学，2007.TANG Yan.The research and application of the time series analysis［D］.Changchun：Northeast Agriculture University，2007.（in Chinese）

［7］ 张世英，王艳晖，杨尊琦.时间序列预测的状态空间方法［J］.预测，1995（3）：70-72.ZHANG Shiying，WANG Yanhui，YANG Zunqi.State space method of time series［J］.Forecasting，1995（3）：70-72.（in Chinese）

［8］ 杨兆升，朱 中.基于卡尔曼滤波理论的交通流量实时预测模型［J］.中国公路学报，1999，12（3）：63-67.YANG Zhaoshen，ZHU Zhong.A real-time traffic volume prediction model based on the kalman filte-ring theory［J］.China Journal of Highway and Transport，1999，12（3）：63-67.（in Chinese）

［9］ 李 嘉，刘小兰.基于卡尔曼滤波理论的交通信息预测模型及其应用［J］.中南公路工程，2006，30（4）：108-109.LI Jia，LIU Xiaolan.A prediction model of traffic information and its application［J］.Central South Highway Engineering，2006，30（4）：108-109.（in Chinese）