一类用常微分方程描述的带接种的SEIR传染病模型稳定性研究
王鸿章,梁聪刚
(平顶山学院 数学与信息科学学院,河南 平顶山 467000)
1 模型的建立
为了研究方便,不妨用S(t),E(t),I(t),R(t)表示t时刻易感类、潜伏类、染病类和康复类人口的年龄密度函数.假设所有新生婴儿和新迁入的人口都是易感类,设为定常数∧,则传染病的流行过程可由如下的常微分方程组来描述[1-4]:


其中β表示疾病的传染率,f表示对易感者的接种率,μ表示人口自然死亡率,ε-1表示平均潜伏周期,r表示病人的康复率(r-1表示平均感染周期).
把系统(1)中的各式相加得:

由(2)式得:
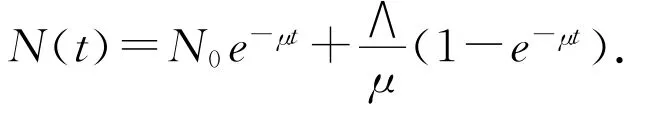
1.1 平衡点
系统(1):的平衡点P*=(S*,E*,I*,R*)满足:

经计算可得系统(1)总存在无病平衡点:


其中:

1.2 平衡点的稳定性证明
为了证明方便,不妨引入一些符号记为:

引理1(文献)[5]假设f:[0,∞)→R是有界的,k∈L1(0,∞),则

引理2(文献[5]) 假设f:[0,∞]→R有界和二次可微,且二阶导数有界,若当n→∞时,t→ ∞,且f(tn)→f∞,则

定理1 当R0<1时,无病平衡点局部渐近稳定;当¯R0<1时,无病平衡点P0全局渐近稳定.
证明 当R0<1时的情况.则其雅克比矩阵为:
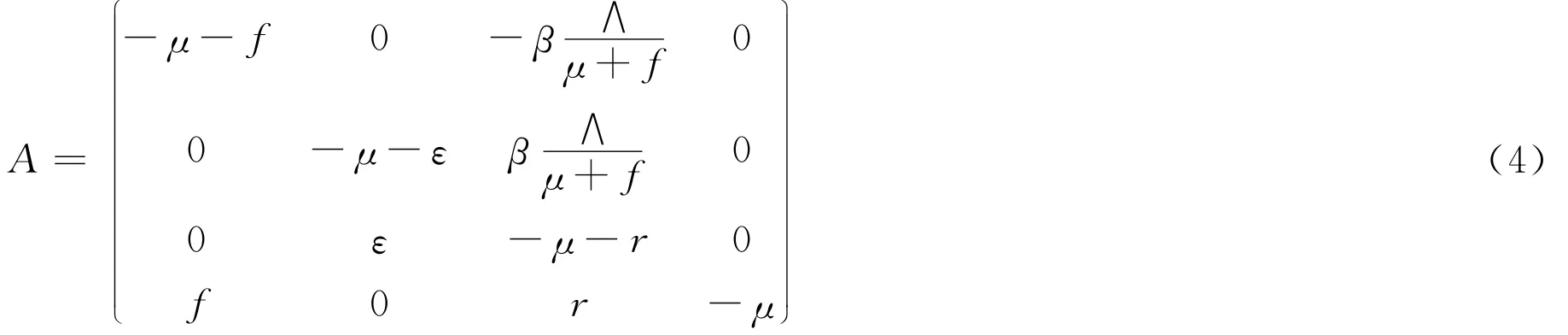
则(4)式在P0处的特征方程为:

显然上面的方程有两个特征根为λ1=-μ-f,λ2=-μ,其余特征根满足:

明显当R0<1时有C>0,又B>0,因此方程(4)λ2+Bλ+C=0不存在实部大于或等于零的根,即当R0<1时,无病平衡点局部渐近稳定.
由(1)式的E′(t)=βS(t)I(t)-μE(t)-εE(t)和I′(t)=εE(t)-μI(t)-rI(t)两个方程得:

在(6)式的各不等式两边取上极限得:


从而当R¯0<1时,有:


由(7)、(8)式有:
由引理2:假设f:[0,∞)→R有界和二次可微,且二阶导数有界,若当n→∞时,tn→∞,且f(tn)→f∞,则


选取数列tn→∞,sn→∞,使得S(sn)→S∞,S(tn)→S∞,S′(sn)→0,S′(tn)→0,因为当tn→∞时,I(t),E(t)都趋于零,所以由(1)式的第一个方程,S′(t)=∧-βS(t)I(t)-μS(t)-fS(t),有:

从而

因此,当¯R0<1时,无病平衡点全局吸引,证毕.
定理2 当R0>1时,系统传染病不消亡的平衡解局部渐近稳定.

代入系统(1)的

显然,(12)等价于(1).
系统(12)在传染病不消亡的平衡点P*处的雅可比矩阵为:


将(13)代入(14)式有:

从而(12)在P*处的特征方程为:


显然a0,a1,a2均为正,传染病不消亡的平衡点局部渐近稳定的充要条件是方程λ3+a2λ2+a1λ+a0=0的所有特征根具有负实部,由Routh-Hurwits判别法[8],这等价于:

我们这里a3=1,易知这些条件全部满足.事实上,Δ2=a1a2-a0>0成立是因为展开括号后负项全部消掉了.
于是这就证明了传染病不消亡的平衡点是局部渐近稳定的.
2 结论
通过研究可以发现传染病是由寄生物所引起的能在人群中相互传播的疾病,因为它能使很多人在一定的时间内降低或散失劳动能力,造成部分人的终生残疾或死亡。所以本文应用仓室建模的思想结合疾病产生的过程情况,利用常微分方程建立起描述的SEIR传染病模型,利用泛函分析和雅克比矩阵证明了模型方程平衡解的存在性和稳定性.应用Routh-Hurwits判别法讨论分析了平衡解的局部稳定性.结果发现:当R0<1时,无病平衡点局部渐近稳定;当¯R0<1时,无病平衡点P0全局渐近稳定.当R0>1时,系统传染病不消亡的平衡解局部渐近稳定。结合其结果来对流行性疾病分析其发生流行的原因,并对其流行的关键因素进行预测,力图找到其流行的规律,并对其规律进行研究找到对流行性疾病进行控制和防治的最优策略办法,为人们防治决策提供理论基础和数量依据[6-8]。
[1] 徐文兵.某些传染病系统的建模、分析与控制研究[D].北京:北京信息控制研究所,2005.
[2] 由守科,闫萍.一类具有潜伏期和染病年龄的SEIR传染病模型[J].新疆大学学报(自然科学版),2010,3(27):288-297.
[3] 杨小平.状态依赖的脉冲微分方程模型的最优周期控制策略[J].河南科学,2013,31(03):262-264.
[4] 唐文艳,焦建军.具脉冲扩散效应的Gomportz种群动力学模型研究[J].湘潭大学学报自然科学版,2013,(2):10-13
[5] H L Liu,H B Xu,J Y Yu,G T Zhu,Stability Results on Age-Structured SIS Epidemuc Model with Coupling Impulsive Effect[J].Discrete Dynamics in Nature and Society,2006(1):1-10.
[6] H L Liu,J Y Yu,G T Zhu,Global Asymptitic Stable Eradication for the SIV Epidemic Model with Impulsive Vaccination and Infection-Age[J].Journal of Systems Science and Complexity,2006,19(3),393-402.
[7] 王鸿章.一类带有感染年龄SIR模型最优化免疫策略的存在性[J].数学的实践与认识,2014,2(44):156-165.
[8] 姜启源.数学模型[M].2011.

