基于拉格朗日原理天线系统动力学模型建立
周洪波,贾艳霞
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.河北省水利水电第二勘测设计研究院,河北 石家庄 050021)
动力学模型建立有很多方法,现在广泛流行的有哈密尔顿原理、广义哈密尔顿原理、拉格朗日原理、牛顿-欧拉方程、有限元等。本文主要讨论基于拉格朗日原理建立天线系统的动力模型。
拉格朗日方程:对于完整系统用广义坐标表示的动力方程,通常是指第二类拉格朗日方程,由法国数学家J.L.拉格朗日首先导出。在本文中,首先为天线建立转角空间的坐标系(二维坐标系),然后利用拉格朗日原理建立其动力学模型。通过定义Jacobian(雅克比)矩阵,建立转角空间和操作空间的映射关系,可以认为此时雅克比矩阵的物理意义就是转角空间到操作空间的传递矩阵。从而得到笛卡尔坐标系下的动力学模型。
1 拉格朗日原理
利用拉格朗日原理,拉格朗日方程是建立动力学模型的理论基础之一,而拉格朗日乘子法只是拉格朗日的一个延伸和拓展,得到一个有限维的动力学模型。一般而言,根据拉格朗日方程建立模型的步骤为:
1)选定广义坐标,建立有限维模型,一般是选择关节变量和柔性连杆的模态坐标为广义坐标;
2)建立动能、势能和虚功表达式;
3)对拉格朗日方程进行必要的推导和整理。拉格朗日方程如下:

其中L为拉格朗日函数,是总动能与总势能之差。
从实质上来讲,利用广义哈密尔顿原理还是利用拉格朗日原理建立系统的动力学模型,其方法实质是一样的,只是适应的场合不同。
2 天线动力学模型
实际天线是工作在三维空间,并且,面天线多是一个圆弧面,现在的天线面多采用炭纤维材质,故而,可以将其等效为一个非线性刚体。为了简化,只建立二维空间的坐标系,如图1所示。
本模型符号说明:
l1:天线Y的长度;l2:天线倾斜的长度;
ρi:天线倾斜、Y的密度;Ii:天线倾斜、Y的转动惯量;
EiIi:天线倾斜、Y的抗挠刚度;θi:天线倾斜、Y角;
τi:倾斜电机、Y电机的转矩;Ti:倾斜轴和X轴的动能;
Vi:倾斜轴、X轴的势能;nPm:天线第m个节点在第n个坐标系下的坐标;
nRm:天线第m个节点在第n个坐标系下的坐标变换阵;
nTm:天线第m个节点在第n个坐标系下的状态转移阵;
其中i=1,2,m,n=1,2。
(1)倾斜轴的动能:
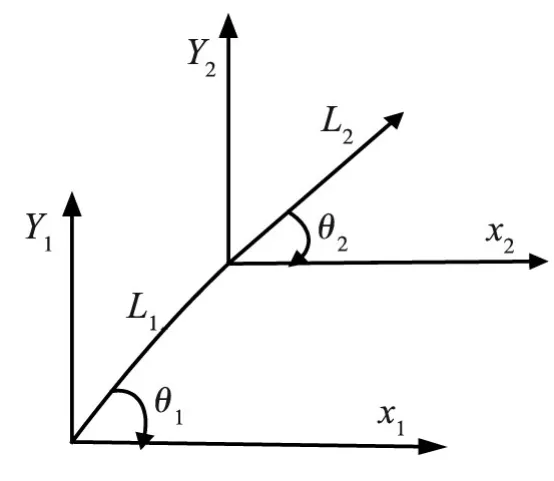
图1 天线模型坐标示意图
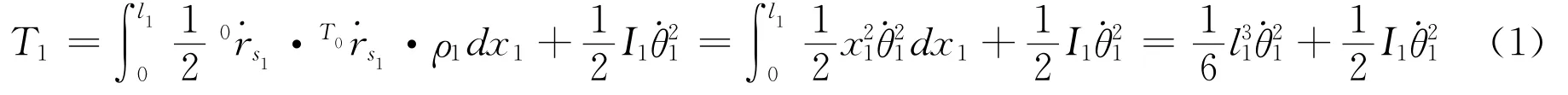
(2)倾斜轴的势能:
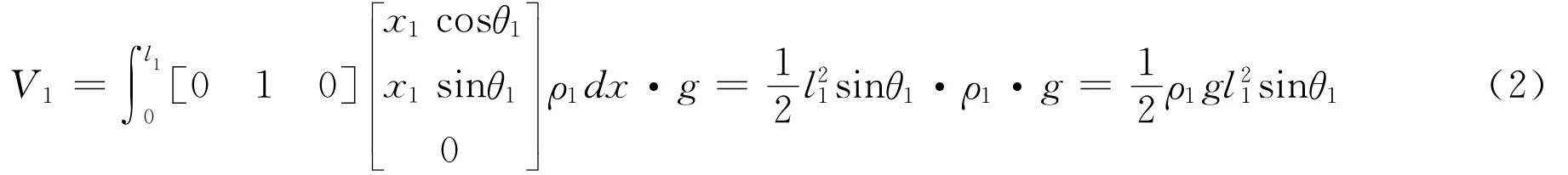
(3)Y轴的动能:
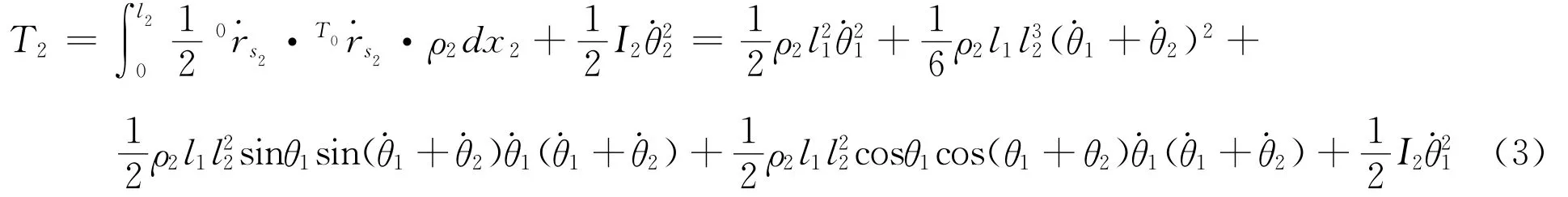
(4)Y轴的势能:
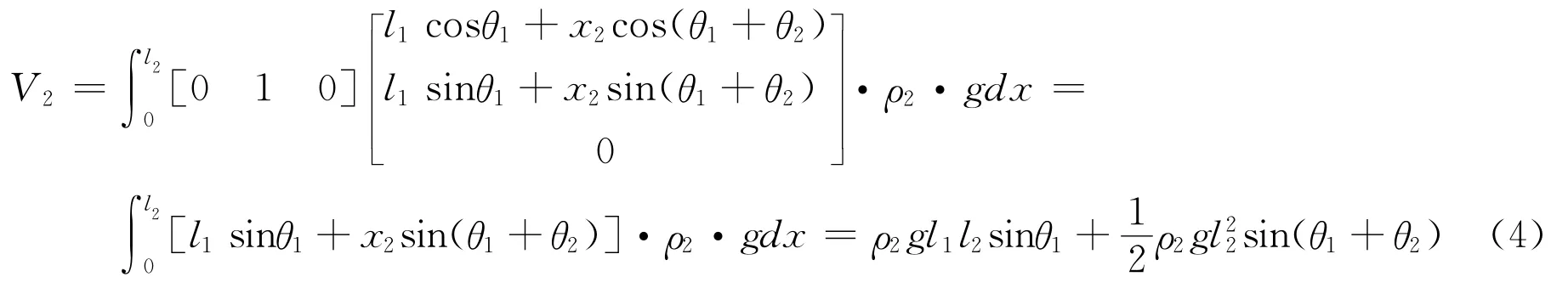
用系统的总动能减去系统的总势能得到拉格朗日函数:
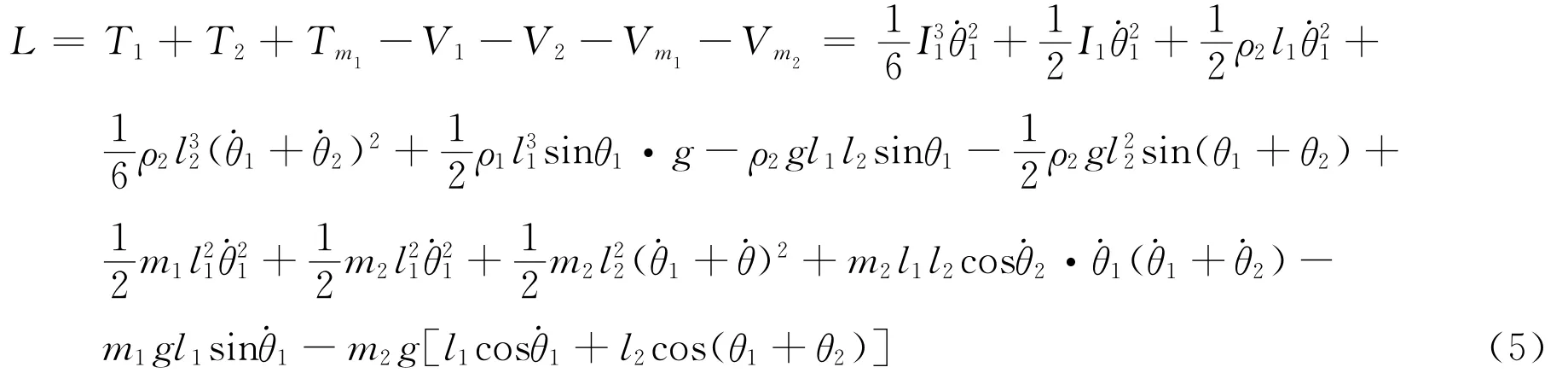
把以上拉格朗日函数代入到以下拉格朗日方程中

得到

式(7)和式(8)共同构成了天线的动力学方程。
3 结束语
本研究把传统的AE座架形式的天线,等效为双自由度刚体,建立拉各朗日函数,并利用拉各朗日原理建立动力学模型。
[1] 林昌禄主编.天线工程手册[M].北京:电子工业出版,2002.
[2] John D.Kraus,Ronald J.Marhefka著.天线(第三版)[M].北京:电子工业出版社,2006.
[3] 牛瑞燕,赵曜.智能二自由度内模控制[J].控制理论与应用,2001,18(4):624-628.
——《势能》

