浅海中利用舰船轴频电场定位技术研究
张学峰,李 涛
(1.91388部队94分队,广东 湛江 524022;2.海军工程大学 电气学院,湖北 武汉 430033)
舰船是由不同金属材料建造的,在海水中会存在腐蚀现象,为了保护船体不受腐蚀,就采取了各种防腐措施,舰船由腐蚀和防腐产生的电磁信号,可在海水中进行一定距离的传播,是舰船不可忽视的目标特征。
舰船电场通常可分为两类:静电场和交变电场。基于舰船静电场对水中目标进行识别和定位已有一定的研究成果,但静电场信号特征较少,易受外界干扰等特点[1-2],使用静电场对目标进行定位受到很大的限制。舰船交变电场主要是由轴频电场组成,轴频电场是一种以螺旋桨旋转频率为基频的时谐电磁场,由于它的不可避免和传播距离远的特性,是一种可以被远程探测的舰船物理场[3-5]。把海水看做线性、均匀、各向同性的无限大半空间,舰船在海水中运动时产生的轴频电磁场可以用低频时谐电偶极子进行建模[6-8]。所以,利用时谐电偶极子产生的电磁场对其进行定位是研究利用舰船在海水中产生的轴频电场信号对舰船进行跟踪定位的基础。
1 定位原理
利用电场传感器对分层介质中运动的水平时谐电偶极子进行定位的方法就是根据该时谐电偶极子的已知参数,包括电偶极距、频率等,以时谐形式的麦克斯韦方程组和分层介质中时谐电磁场的边界条件等建立分层介质中运动的水平时谐偶极子电场的模型,再采用合适的优化算法,利用电场传感器测得三个以上固定场点的三分量电场模值进行推算反演,进而求得传感器与场源电偶极子的距离。
如图1所示,浅海中三个电场传感器对场源进行目标定位,在海水中有一个以速度v运动的水平时谐电偶极子P,以及三个电场传感器A,B,C,这时可在水平时谐电偶极子所处位置(即场源)建立坐标系S,S坐标系的xoy平面位于海平面上,z轴垂直于海平面,方向向下。取海水的深度为d,则在S坐标系下,z<0为0区,0<z<d为1区,z>d为2区,0区、1区和2区分别对应空气、海水和海底三种介质。则该运动的水平时谐电偶极子P在某一时刻(t=t0)的坐标可表示为:
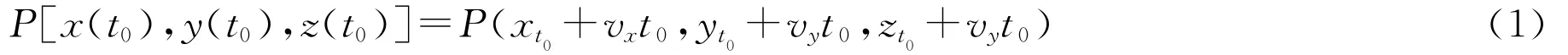
式中[x(t0),y(t0),z(t0)]表示初始时刻(t=0)的场源P在S坐标系下的坐标,vx,vy,vz分别表示运动水平时谐电偶极子P在x,y,z三个方向的速度分量。
另外,三个电场传感器A,B,C在S坐标系下的坐标可以分别表示为A(x1,y1,z1),B(x2,y2,z2)和C(x3,y3,z3)。且在t=t0时刻,三个电场传感器A,B,C测得的电场模值分别为(|Ex1|,|Ey1|,|Ez1|)、(|Ex2|,|Ey2|,|Ez2|)和(|Ex3|,|Ey3|,|Ez3|)。

图1 三个传感器与电偶极子位置关系示意图
浅海中时谐水平电偶极子电场表达式如下[7,9]:


由上述电场解析式可知,在空间坐标系S中,海水介质中场源P(x0,y0,z0)产生的三分量电场模值可以表示为与源点和场点相对位置参数有关的三个非线性方程,如下:

式中,(x0,y0,z0)表示S坐标系下运动的水平时谐电偶极子(即场源)在某一时刻(t=t0)的坐标点,(xm,ym,zm)表示S坐标系下传感器所在的坐标。
为方便目标定位,同时不影响实际情况,不妨使某时刻(t=t0)该水平时谐电偶极子处于坐标系S的z轴上,且使坐标系S的x轴正方向与该水平时谐电偶极子P的方向相同,则该时刻场源P在S坐标系下的坐标可表示为P(0,0,z0)。又由于实际情况中,三个电场传感器在海水中的深度是已知的,则可设电场传感器A,B,C的深度分别为l1,l2和l3,于是,电场传感器A,B,C的坐标可分别表示为A(x1,y1,l1),B(x2,y2,l2)和C(x3,y3,l3)。再将场源P和传
感器A,B,C的坐标代入到式(5)中可得:
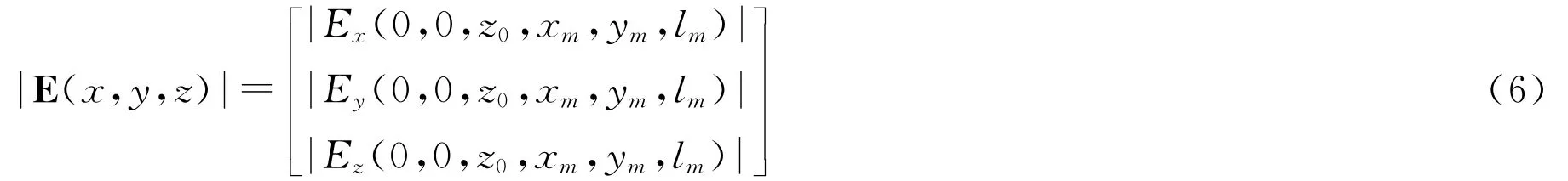
式中,lm表示传感器的深度。从式(6)中可以看出三个等式中有三个未知量是需要求出的,分别为水平时谐电偶极子的深度z0,传感器在坐标系S下的横坐标xm和纵坐标ym。这三个非线性方程中三个未知量的求解可以借助优化算法求得。
计算出场源深度和传感器坐标后,便可以计算出三个电场传感器A,B,C到场源P的距离为:

从上面的公式可以看出,虽然时谐偶极子的空间电场分布具有对称的特性,一个时谐偶极子的周围有多个点的三分量电场模值相等,但是在设定的坐标系S下,传感器的横坐标xm和纵坐标ym无论正负都不影响传感器A,B,C到场源P的距离的计算结果,此外,由于该水平时谐电偶极子位于海水中,所以它的深度z0一定是大于0的,这样就可以大大缩小优化算法中该时谐偶极子深度z0,传感器的横坐标xm和纵坐标ym的搜索范围,同时可以排除多解的情况。
如图2所示,再建立已知的传感器坐标系S′,电场传感器A,B,C在S′坐标系下的坐标分别为A(x1′,y1′,z1′),B(x2′,y2′,z2′),和C(x3′,y3′,z3′),且都为 已 知。 场 源P在S′坐标系下的坐标为P(x,y,z),为未知。

图2 三个传感器定位电偶极子的示意图
以电场传感器A,B,C所在位置为圆点,再分别以传感器到场源P的距离dA,dB,dC为半径,作三个球形,在不考虑三个传感器的时钟差的情况下,可得在S′坐标系下三个传感器到场源距离的公式为:

从式(8)、(9)和(10)求解出的交汇点(x,y,z0)即为待求的场源P的坐标。
这里需要说明的是,虽然式(8)、(9)和(10)三个等式中只有两个未知量,但是,如果只用其中的两个等式去求解场源的x和y坐标,就可能会出现x和y坐标有两组不同的解情况,造成了场源坐标在S′坐标系下的解不唯一,所以采用三个传感器去定位场源坐标是必要的。
另外,考虑到实际情况中,受海洋环境因素、其他场源干扰以及电场传感器的测量误差等影响,由上面求得的电场传感器到场源P的距离dA,dB,dC存在一定的误差,所以从式(8)、(9)和(10)直接求解出交汇点(x,y,z)比较困难。但是可以借助优化算法,求解出一个误差最小的交汇点,这一点即为场源P在S′坐标系下的坐标。
2 基于GAPSO混合算法的位置参数求解
遗传算法(Genetic Algorithm,缩写为GA)是以自然选择和遗传理论为基础的高效的全局寻优搜索算法,为求解非线性、多模型、多目标等复杂系统优化问题通用框架,遗传算法具有并行搜索的能力,变异和交叉可以保证种群的多样性,缺点是收敛速度较慢,局部搜索能力弱、精度也较低,仿真试验中运行时间较长。微粒子群算法(Particle Swarm Optimization,缩写为PSO)是一种基于迭代的优化算法,系统初始化一组随机解,通过迭代寻找最优解,它具有规则简单、精度高、收敛快等优点,但是它没有交叉和变异操作,如果初始种群随机选择不好则容易出现陷入局部最优的情况,从而无法搜索到全局最优解。
为充分发挥出两种算法的优势,本文将两种算法的优势结合,形成了遗传粒子混合算法,简称为GAPSO混合算法[12]。
由于|Ex|和|Ey|比|Ez|大两个或一个数量级,尤其是场点和传感器距离较远时,z方向的电场模值与x和y轴方向电场模值的数量级相差较大,也就意味着存在x、y、z三个方向电场模值对拟合误差的贡献不一样,可定位度小的分量拟合误差较大,可定位度大的分量拟合误差较小,所以需要经过修正使他们的电场值在一个数量级上,以防止出现对某些分量过度拟合而其他分量误差较大的情况。因此可以设定目标函数为:
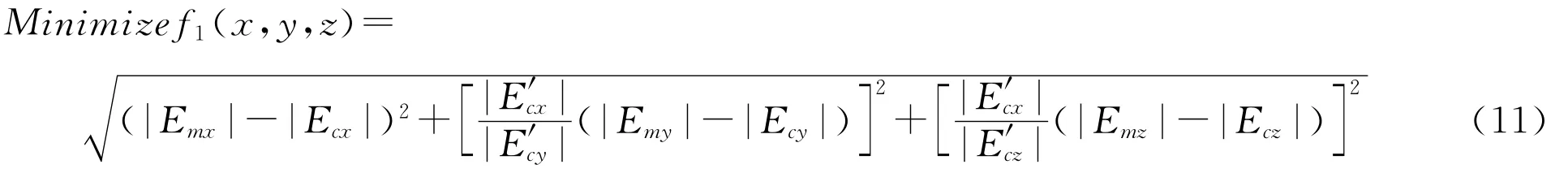
其中,|Emx|,|Emy|,|Emz|为空间某传感器(x,y,z)的电场测量值,|Ecx|,|Ecy|,|Ecz|为该点的电场计算值,|E′cx|,|E′cy|,|E′cz|是该点电场计算值保留两位有效数字后的值,采用上面的目标函数便可以有效解决x、y、z三个方向电场模值对拟合误差的贡献不一样的问题。
由于计算得出某一时刻的三个传感器到场点的距离一般不存在数量级相差很大的情况,可以设定目标函数为:

其中,dA,dB和dC表示由第三步得到的场点到源点距离的测量值,d′A,d′B和d′C为优化计算过程中场点到源点距离的计算值。
3 仿真分析
如图4所示,假定在浅海中有一个运动的水平时谐电偶极子P,其频率为1Hz,运动速度为5m/s,大小为1A·m。在t=t0时刻,电偶极子P在S坐标系下的坐标为(0,0,z0),取z0=20,同时设三个电场传感器A,B,C在S坐标系下的坐标为A(-500,800,30),B(1000,-600,40),C(300,400,50),取空气中的三个电磁参数分别为:电导率σ0=0,介电常数ε0=(1/36π)×10-9F/m,磁导率μ0=4π×10-7H/m;海水中:电导率σ1=4Ω/m,介电常数ε1=80ε0,磁导率μ1=μ0;海床:电导率为σ2=0.04Ω/m,介电常数为ε2=8ε1,磁导率为μ2=μ0。

图3 GAPSO算法流程图

图4 三个传感器的位置示意图
又由于实际情况中,三个电场传感器的相对位置是已知的,所以,需要再建立一个图2中已知的坐标系S′,电场传感器A,B,C在S′坐标系下的坐标分别为A(-600,-500,30),B(800,1000,40)和C(-200,300,50),场源P在S′坐标系下坐标为(x,y,z0),通过三个传感器间距离计算可以验证A,B,C在坐标系S和S′下的距离是相等的。
利用运动水平时谐电偶极子在浅海环境下的电场解析式可以计算出电场传感器在A,B,C三点的电场模值分别为:|E1x|=7.2143×10-10V/m,|E1y|=1.4554×10-10V/m,|E1z|=1.9820×10-12V/m,|E2x|=6.4516×10-10V/m,|E2y|=1.5173×10-10V/m,|E2z|=1.1931×10-12V/m,|E3x|=1.5319×10-9V/m,|E3y|=2.6610×10-10V/m,|E3z|=2.6106×10-11V/m。
在场点位置寻优时,设定寻优范围为10m<x<2000m,10m<y<2000m,0<z<100m。经多次反复试验后,设定PSO算法参数:粒子范围宽度为0.8,两个加速因子都为2,惯性因子随着迭代次数的增加在1.4到0之间逐步减小。GA算法:选择概率为0.5,交叉概率为0.7,变异概率为0.1。此外,个体长度为3,为保证种群的多样性,设定种群数量为200,迭代次数为30次。
多次迭代后,即可输出场源深度z0及场点横坐标和纵坐标的最优解。图5即为迭代过程中目标函数值Minimizef1(x,y,z)及时谐偶极子深度z0和A,B,C三点的横坐标xm,纵坐标ym的变化过程。
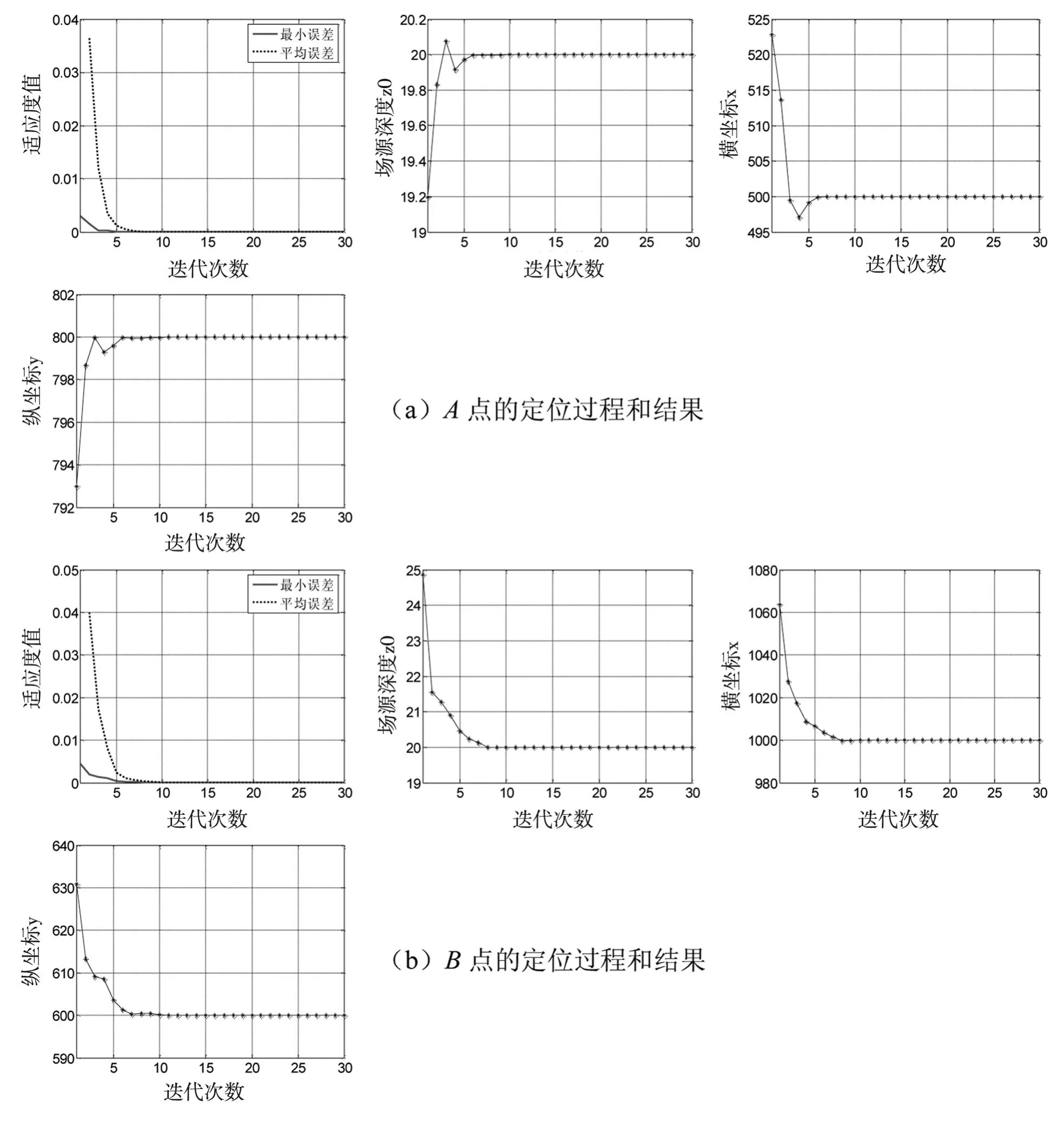
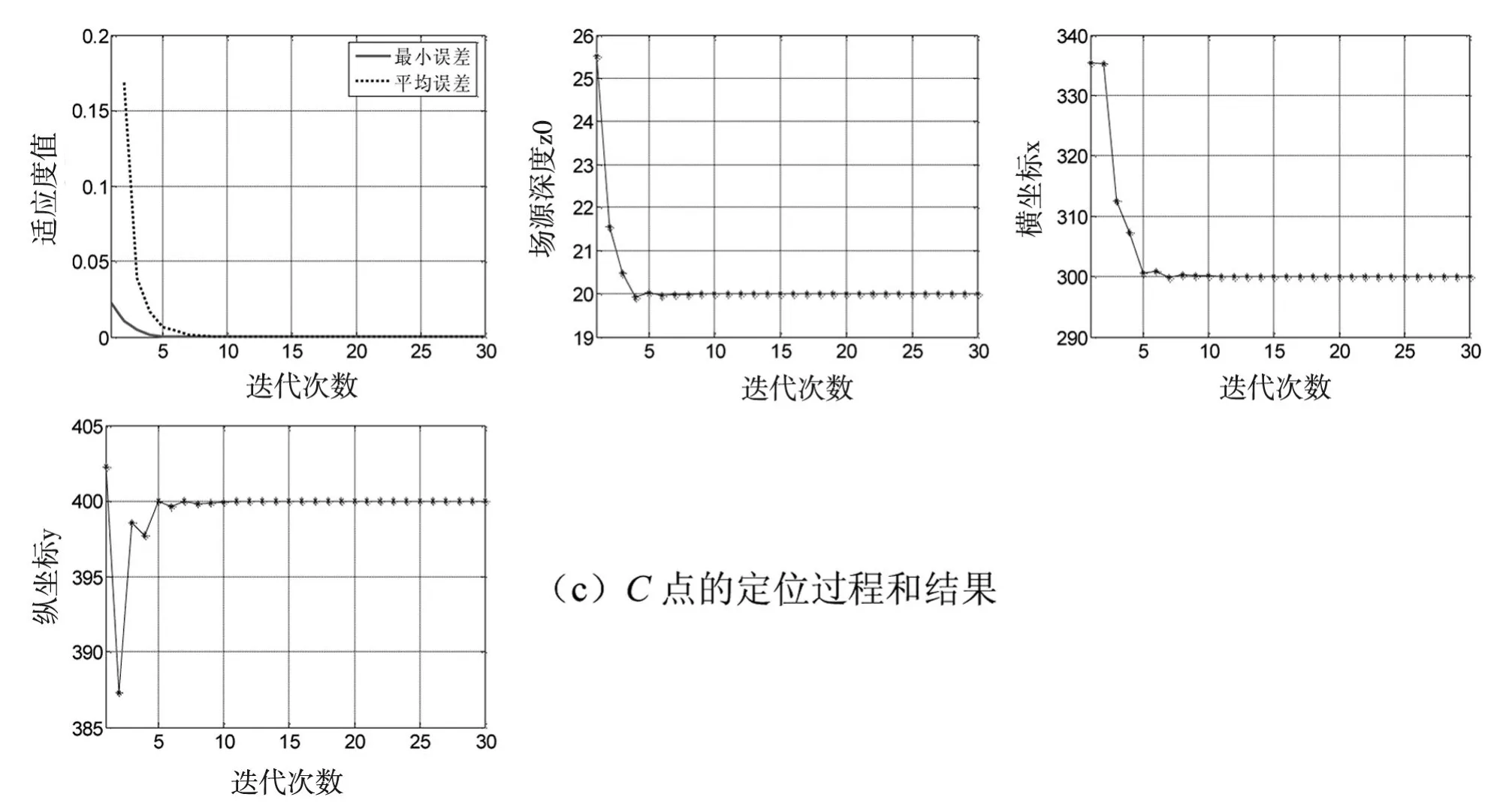
图5 浅海中A,B,C三点的定位过程和结果
由图可见,目标函数的收敛速度非常快,在迭代10次后,场源深度z0及A,B,C三点的横坐标xm和纵坐标ym的变化趋于平稳,而且精度非常高。A点在S坐标系下的坐标为(500,800,30),B点在S坐标系下的坐标为(1000,600,40),C点在S坐标系下的坐标为(300,400,50),场源深度z0都为20。同时求得三个电场传感器到场源的距离分别为:dA=943.4511m,dB=1166.4000m,dC=500.8992m。
设定寻优范围为-2000m<x<2000m,-2000m<y<2000m,迭代次数为20次,其他算法参数设置与上一步相同。
多次迭代后,即可输出场源坐标在S′坐标系下的最优解。图6即为迭代过程中目标函数值Minimizef2(x,y,z)及场源的横坐标x,纵坐标y的变化过程。

图6 浅海中S′坐标系下场源坐标的定位过程和结果
S′坐标系下场源坐标的定位结果为P(200,0,20),通过在S和S′坐标下场源与传感器的距离可以验证场源坐标定位是非常精确的。
4 结论
本文研究了浅海中基于水面舰艇轴频电场的定位方法,提出了利用海水中三个电场传感器来确定目标的位置的定位方法,从仿真结果来看,通过文中提出的反演方法和迭代算法,可以很精确地确定目标的位置坐标,运用文中所提出的方法在对目标进行定位是完全可行的。
[1] 周骏.海水中电磁场的特性及舰船电磁场[D].武汉:海军工程大学,1999.
[2] Dou Ji,Xiang Jun Wang,Wen Bao Liu.The Propagation of Horizontal Static Dipole Electromagnetic Field in Shallow Sea[C].Electromagnetic Field Problems and Applications(ICEF),2012.
[3] 汪小娜,肖昌汉,王向军,嵇斗.运动潜艇的感应电场分布[J].海军工程大学学报,2012,24(4):7-10.
[4] 汪小娜,肖昌汉,王向军,嵇斗.沿任意方向运动的磁偶极子感应电场特性[J].舰船科学技术,2012,(12):19-23.
[5] 朱武兵,嵇斗,王向军,柳懿.浅海中影响运动舰船轴频电磁场的因素[J].船电技术,2013,(11):41-44.
[6] 龚沈光 卢新城.舰船电场特性初步分析[J].海军工程大学学报,2008,2(20):1-5.
[7] 毛伟,张宁,林春生.在三层介质中运动的时谐水平电偶极子产生的电磁场[J].电子学报,2009,(9):2077-2081.
[8] Xiang Jun Wang,Yi Liu,Dou Ji.The Research of Electric Field Based on Ring Current Source Model[J].Applied Mechanics and Materials,2012,622:661-664.
[9] 雷银照.时谐电磁场解析方法[M].北京:科学出版社,2000.
[11] Li S Q,Chan C H,Huang C C.Closed-form spatial electric field Green's functions of microstrip structures using the fast Hankel transform and the matrix pencil method[J].IEE Proc.Microw.Antennas Propag,2000,147(3):161-166.
[12] 彭晓波,桂卫华,黄志武,等.GAPSO:一种高效的遗传粒子混合算法及其应用[J].系统仿真学报,2008,18:5025-5027.

