一类基于二维线性插值函数的改进Canny算法

李 健，李俊杰，任宪盛，陈冰冰，付浩威

(1.吉林农业大学信息技术学院，吉林 长春 130118；2.吉林省生物信息学研究中心，吉林 长春 130118；3.吉林大学第二医院骨科，吉林 长春 130041)

一类基于二维线性插值函数的改进Canny算法

李 健1，2，李俊杰1，2，任宪盛3，陈冰冰1，2，付浩威1，2

(1.吉林农业大学信息技术学院，吉林 长春 130118；2.吉林省生物信息学研究中心，吉林 长春 130118；3.吉林大学第二医院骨科，吉林 长春 130041)

利用Canny算法对腰椎间盘的核磁共振(MR)图像进行边缘检测，实现了计算机辅助治疗.针对MR图像由于人体结构复杂性导致的成像后的灰度不统一的问题，在Canny算法计算检测之前，引入二维线性插值函数，实现图像灰度的统一化，并使用均值滤波函数代替传统算法中的高斯滤波函数，改进了传统的Canny算法.实验结果表明，改进后的Canny算法有效地减少了腰椎间盘MR图像中非真实边缘检出的概率.

图像处理；边缘检测；Canny算法；二维均值插值函数

图像边缘检测[1](Image Edge Detection)起源于1965年Roberts提出基于提取高频信号进行检测的Roberts算子[2]，Prewitt和Sobel相继提出了Prewitt算子[3]和Sobel算子[4].这些算子在检测没有噪声的图像边缘时，能够实时、准确地检测出图像边缘，且运算过程简单，但是，当被检测的图像含有噪声时，由于算子对图像噪声不敏感，很难区分图像的噪声和边缘，因此边缘检测精度不高.在实际处理图像时效果并不理想.相比这些微分算子，基于最优化算法的Canny算法[5]因具有信噪比大和检测精度高等优点而被广泛采用，并且成为评价其他边缘检测方法的标准.

核磁共振成像[6](MR)是医学成像技术中的一种，它利用磁共振现象从人体中获得电磁信号，并重建人体信息.MR已经应用于全身各系统的成像诊断，且对人体几乎没有伤害.同时，相比于CT和X射线成像等其他技术，MR可以做多个切面图，且空间分辨率更高，因此MR图像包含更多信息，而这些信息中有些无法通过人工手段获取，因此利用计算机智能算法辅助处理已经成为一种趋势.

在MR图像中，不同结构的解剖和病理断面是以不同的灰度来显示，同一级灰度表示同一断面.而灰度剧烈变化的地方代表图像边缘，同时也是结构断面的边缘.传统Canny算法在检测一般图像时具有较大的优势，但是对于MR图像具有一定的局限性，原因在于人体结构的复杂性，使得在同一结构内也存在灰度变化，导致在进行计算机处理时，算法识别不准确.因此传统Canny算法在检测时存在非真实边缘以及真实边缘检测模糊的现象.因此，本文对传统Canny算法进行改进，使它对MR图像有较好的适应性.

1 传统Canny算法

Canny算法是F.C.John于1986年开发出来的一个基于最优化理论的多级边缘检测算法.该算法尽可能多地标志出图像中的可能边缘，同时Canny参数允许根据不同的特定要求进行调整以识别不同的边缘，有较好的适应性.

1.1 传统Canny算法步骤

传统的Canny算法包括以下4个步骤：

(1) 一维高斯滤波函数G(x)做平滑图像处理.高斯函数构造方式为

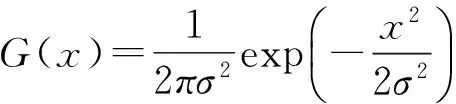
(1)

其中σ为高斯函数的标准差，它控制平滑程度.

(2) 利用2×2邻域内一阶偏导的有限差分计算I(x，y)的梯度幅值M(x，y)和梯度方向H(x，y)，其中：

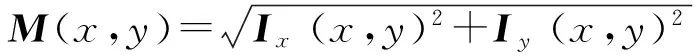
(2)

H(x，y)=arctan(Ix(x，y)，Iy(x，y)).

(3)

2×2邻域模板的形式为

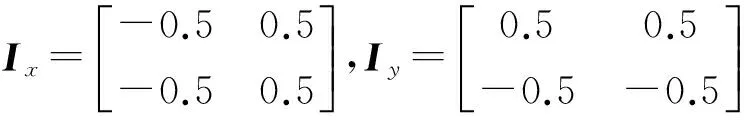
(4)

(3) 对梯度幅值进行非极大值抑制，找到I(x，y)中所有可能的边缘点，将可能点标注为M(x，y).

(4) 对图像M(x，y)进行高、低2个阈值分割，得到2个阈值边缘图像TH(i，j)和TL(i，j).利用递归算法在TL(i，j)中搜集边缘，直到将TH(i，j)中所有的间隙相连接，实现双阈值法检测并连接边缘.

1.2 传统Canny算法存在的缺陷

由于人体组织以及骨骼结构复杂多变，因此在MR图像中的结构内部还存在子结构，这些子结构就属于图像噪声.在Canny算法进行检测过程中，由于一维高斯函数对图像的噪声十分敏感，因此可能导致检测出非真实的情况.基于以上不足，我们对图像进行预处理，并改进传统Canny算法，进一步提高算法的边缘检出率.

2 改进的Canny算法

针对MR图像的特点，本文对传统Canny算法进行改进.为减少传统算法由于噪声敏感性带来的影响，本文从两方面进行算法改进：一方面是针对图像本身的优化，通过引入二维线性插值函数，增加图像细节，减少噪声影响；另一方面，使用均值滤波算子代替传统算法中的高斯滤波算子，解决传统Canny算法的噪声敏感性问题.

2.1 二维线性插值函数

二维线性插值[7]是在一维线性插值的基础上，对矩阵进行横、纵2个方向上的线性插值.这种方法广泛运用于图像以及信号处理领域.

一维插值函数为

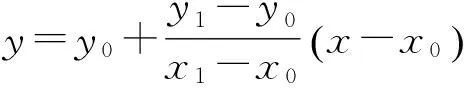
(5)

其中x0和x1为已知的2个点，y0和y1为x0与x1对应的值.插入的点为x，且x0≤x≤x1，则y为插入点x对应的值.

二维线性插值就是在(5)式的基础上扩展到纵轴，即将yi设为自变量，将xi设为因变量.对于像素矩阵来说，有

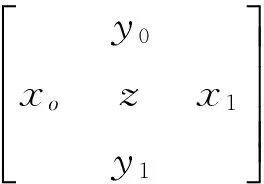
(6)

假设矩阵(6)是像素矩阵的一部分，x0，x1，y0和y1为已知像素，z为插值像素.运用二维线性插值计算z，就需要将z分为zX，zY两部分.zX，zY计算式如下：

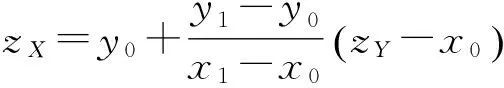
(7)

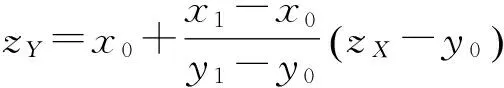
(8)

其中x0≤z≤x1，且y0≤z≤y1.而最终插值结果z=zX+zY.

二维线性插值函数在能够保证图像不失真的情况下，实现图像的扩展和压缩变换，具有较强的鲁棒性(见图1).通过图1可以看出，椒盐噪声结果有明显的改善.

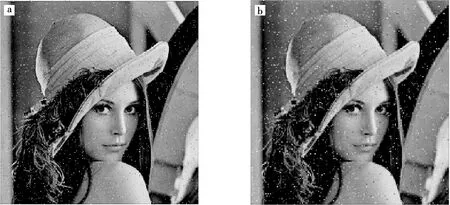
a为加入2%的椒盐噪声；b为经过二维线性插值缩小60%

2.2 基于均值滤波器改进的Canny算法

在传统Canny算法[8-9]中，由于高斯滤波函数的噪声敏性问题，容易导致算法检测出非真实边缘，因此本文考虑使用更为一般的滤波算法——均值滤波算法[10-11].均值滤波虽然计算形式较为简单，但是处理时所涉及的像素点更多，因此能够有效地抑制高斯噪声.且均值滤波算法属于线性滤波的一种，不会改变图像的结构特性，因此不会对原有的真实边缘产生影响.

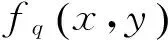
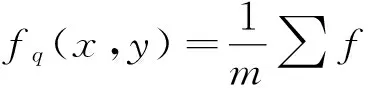
(9)

其中m为当前变换中所包含的像素点的总个数，由于均值滤波器使用的正方形模板，因此m=n2(n为矩阵行列数).

在上述算法过程中，较为关键的步骤就是计算邻域模板M，其计算公式为

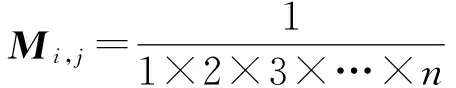
(10)

其中i，j=1，2，3，…，n.给出一个3阶的均值滤波模板为

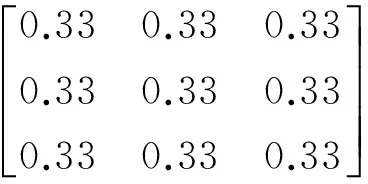
(11)

对于图1中加入椒盐噪声后的Lena图像，本文分别采用2种方法进行处理比较，获得了如图2所示结果.从图2可以明显看出，改进后的Canny算法在保证了原有图像细节的同时，有效地抑制了图像中的椒盐噪声，在传统Canny计算中，椒盐噪声并没有得到抑制.

3 改进Canny算法的应用

3.1 细节图像比较

直接运用传统Canny算法以及改进Canny算法对某病人的2节脊柱的细节图进行处理，结果如图3所示.从图3可以明显看出，在传统Canny算法中，脊柱中间检测出较多的由于灰度变化而产生的边缘，但它们实际属于脊柱内部.但是在改进Canny算法中，这些边缘检出较少.

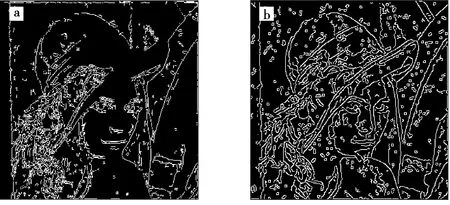
a为改进Canny算法；b为传统Canny算法

a为MR原图；b为传统Canny；c为改进Canny算法

本文统计了2种算法实际检测出的边缘所占的像素值，并通过图像观察找出2种算法存在的缺陷，即不连续边缘所占的像素以及假边缘所占像素，同时统计2种算法的运行时间，得到的数据见表1.

表1 Canny算法数据对比

通过腰椎间盘的MR图像的片段实验以及数据实验对比，对图像进行二维插值函数处理，并运用基于均值滤波改进的Canny算法，在复杂度相近的情况下，能够较为准确地提取出图像边缘.通过数据对比分析，在保证真实边缘检测率接近的条件下，采用本文算法能够抑制46.4%的假边缘.

3.2 完整图像比较

通过细节图像实验对比，改进Canny算法能够较好地处理腰椎间盘的MR细节图像.本文给出完整MR图像对比实验如图4所示.由图4可以看出，运用改进后的Canny算法，对于MR图像中脊柱的处理更为到位，由于进行了2次滤波处理，脊柱中不统一的像素点被较好地过滤掉，且较为完整的保留下了脊柱边缘的信息.对于传统Canny算法，虽然处理后冗余信息较多，但是图像边缘更为光滑，更有利于进一步处理.

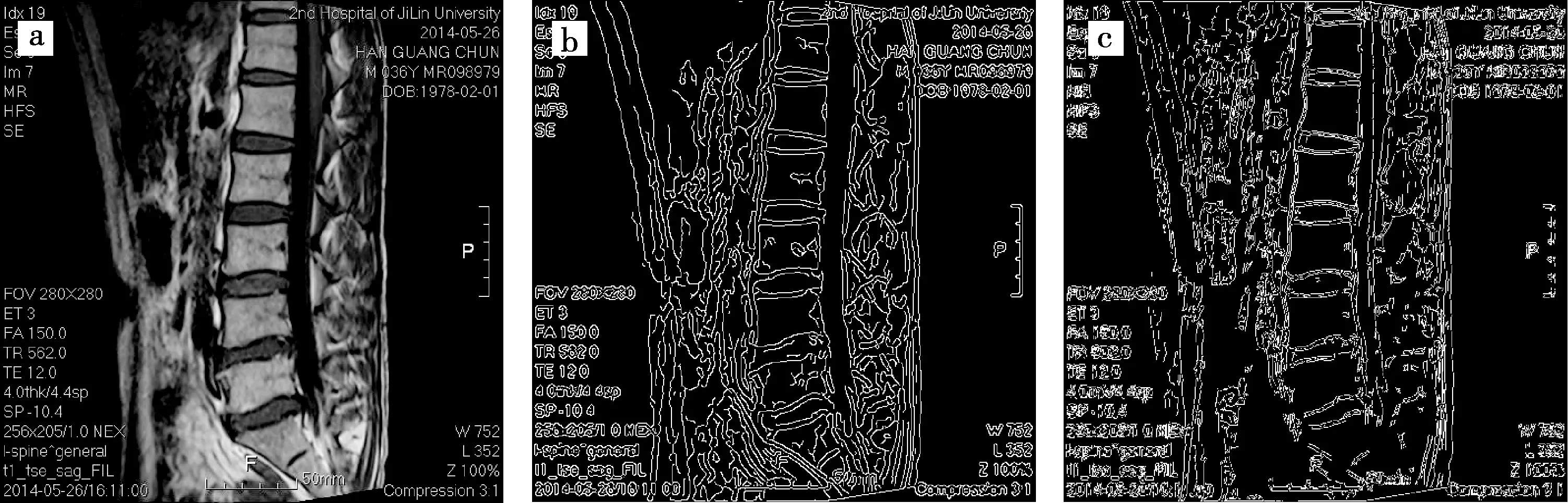
a为原图；b为传统Canny算法检测的图像；c为改进Canny算法

4 结论与展望

本文根据MR图像内部结构不统一的特点，对传统Canny算法进行改进.针对传统Canny算法检测出非真实边缘的情况，本文预先引入二维线性插值函数，对图像进行预处理，使内部结构统一化.然后针对传统Canny算法中高斯滤波器的噪声敏感性问题，提出了基于均值滤波器的改进Canny算法.实验结果表明，运用改进Canny算法进行边缘检测能够有效地解决MR图像内部结构不统一的问题.而且相比于传统算法，改进后的算法在真实边缘检出率、算法复杂度相近的情况下，抑制了46.4%的假边缘.

[1] 陈一虎.图像边缘检测方法综述[J].宝鸡文理学院学报(自然科学版)，2013，33(1)：16-21.

[2] 马宪民，蒋勇.煤矸石二值图像的Roberts快速边缘检测法[J].仪器仪表学报，2005，26(8)：595-597.

[3] YANG LEI，ZHAO DE WEI，WU XIAO YU.An improved prewitt algorithm for edge detection based on noised image[C]//Dallas Image and Signal Processing，International Congress on.Shanghai：IEEE，2011：1197-1200.

[4] PING BO，SU FEN ZHEN，DU YUN YAN.Bohai front detection based on multi-scale Sobel algorithm[C]//Quebec Geoscience and Remote Sensing Symposium (IGARSS).Quebec：IEEE，2014：4423-4426.

[5] WANG BING，FAN SHAO SHENG.An improved Canny edge detection algorithm[C]//Shanghai Computer Science and Engineering，WCSE’09，Second International Workshop on.Shanghai：IEEE，2009：497-500.

[6] KORTEPETER MG.MRIMy Resonant Image[J].The Full Content of Annals is Available to Subscribers，1991，115(9)：749-750.

[7] 王洪英，贾绍河.二维线性插值方法及其在平面温度场计算中的应用[J].天津师范大学学报(自然科学版)，2008，35(3)：74-76.

[8] 史晶，彭进业，王大凯，等.改进的Canny算法及其在图像编码中的应用[J].计算机工程，2009，35(21)：206-207，210.

[9] 邵晓芳，孙即祥，王亮亮，等.改进的Canny算法[J].电光与控制，2006，13(6)：53-55.

[10] 龚昌来.基于小波变换和均值滤波的图像去噪方法[J].光电工程，2007，34(1)：72-75.

[11] 朱维文，赵跃进，朱慧时，等.改进的均值滤波算法在太赫兹成像中的应用[J].红外与激光工程，2013，42(5)：1241-1246.

(责任编辑：石绍庆)

Research on a kind of improved Canny algorithm based on 2-D linear interpolation function

LI Jian1，2，LI Jun-jie1，2，REN Xian-sheng3，CHEN Bing-bing1，2，FU Hao-wei1，2

(1.College of Information Technology，Jilin Agricultural University，Changchun 130118，China；2.Jilin Provincial Center for Bioinformatics，Changchun 130118，China；3.Department of Orthopedic Surgery，Second Hospital of Jilin University，Changchun 130041，China)

In this paper，an edge detection on the MR images of lumbar intervertebral disc(nuclear magnetic resonance) which contributes to realize the computer aided treatment by using Canny algorithm.Aiming at the problem that the gray of MR images is not uniform after imaging which caused by the complexity of the human body structure，2-D linear interpolation function is introduced to realize unified image gray before applying Canny algorithm to calculate and detect.Meanwhile，Gauss filter function in the traditional algorithm is insteaded by mean filtering function to improve the traditional Canny algorithm.The result shows that the improved Canny algorithm effectively reduces the probability of non real edge detection in MR images of lumbar intervertebral disc.

image processing；edge detection；Canny algorithm；2-D linear interpolation function

1000-1832(2015)04-0079-05

10.16163/j.cnki.22-1123/n.2015.04.017

2014-12-24

吉林省科技发展计划项目(20130522110JH，20140204045NY)；吉林省教育厅“十二五”科学技术研究项目(2014第468号).

李健(1981—)，男，博士，副教授，主要从事时空表示与推理、偏微分方程、物联网研究；通讯作者：任宪盛(1974—)，男，博士，主治医师，主要从事脊柱脊髓损伤及疾病研究.

TP 39 [学科代码] 520·6040

A