甜瓜霜霉病斑在叶片上的空间分布格局及抽样技术
段显德,董荣春,王 硕,杨信东
(1.辽东学院农学院,辽宁 丹东 118003;2.吉林农业大学农学院,吉林 长春 130118)
甜瓜霜霉病斑在叶片上的空间分布格局及抽样技术
段显德1,董荣春1,王 硕2,杨信东2
(1.辽东学院农学院,辽宁 丹东 118003;2.吉林农业大学农学院,吉林 长春 130118)
通过扩散系数和聚集指数两个空间分布型指标及平均拥挤度和均值的回归关系,研究了甜瓜霜霉病斑在叶片上的空间分布格局.结果表明:甜瓜霜霉病初侵染的病斑在叶片上呈现随机分布,再侵染的病斑呈现聚集分布.随着病斑数的增加,所需抽样数递减.序贯抽样模型为T(高/低)=0.1N±0.682N1/2.调查叶片为N片时,若累计病斑数超过上限则可确定为需防治田圃;未达到下限时,可确定为不需防治田圃;如在上下限之间,则应继续调查.采用集聚指数和均值数据进行相关分析,判断甜瓜霜霉病病斑在叶片上的集聚程度与病害发生程度间的相关性,可以取代Taylor幂法则等其他判断聚集强度与种群密度相关性的方法.
甜瓜霜霉病;空间分布格局;理论抽样数;序贯抽样检索表
甜瓜霜霉病是瓜类生产上一种重要的世界性病害,致病菌古巴假霜霉菌(PseudoperonosporacubensisRostov)是一种专性寄生菌.在自然条件下该病菌能够侵染甜瓜、黄瓜、西瓜、南瓜等多种葫芦科植物,其中以甜瓜、黄瓜、西瓜等受害最为严重.该病最早在古巴发现,1869年英国的Berkeley首先对Charles Wright在葫芦科蔬菜上采集的一种寄生菌病害进行了描述并定名.1888年日本的田中在东京首次报道了黄瓜霜霉病.1889年在美国新泽西的黄瓜生产过程中,霜霉病造成了严重危害,同年有报道指出,在日本和美国报道的霜霉病是由同一种病原菌侵染引起的.[1]此后,有70多个国家相继发现了霜霉病.甜瓜霜霉病可依靠气流进行远距离传播[2],在适宜条件下,流行性强、传播速度快、发病重且有毁灭性.该病在露地和保护地都普遍发生,尤其以保护地栽培的黄瓜、甜瓜受害损失最为严重,对瓜类生产威胁极大.各国学者相继对病原菌的生物学特性[3-5]、寄主植物的抗性[6-8]、病原菌抗药性[9-10]、霜霉病的发生危害及综合防治等多方面做了大量研究工作[11-12],但在流行规律方面研究较少[13-14],还有不少流行学问题尚未明确.目前,对甜瓜霜霉病斑在叶片上的空间分布格局及抽样技术方面的工作,还没有人做过系统研究.因此,我们参照其他病害的相关研究[15-17],对甜瓜霜霉病斑在叶片上的空间分布格局及抽样技术进行了研究,以为病害的分析及预测防治提供科学依据.
1 材料与方法
1.1 空间分布格局的测定方法
田间实验在吉林农业大学实验站植保专业教学基地进行,室内实验在吉林农业大学农学院植物病理实验室进行.
2009年7月25开始调查,共进行3次调查,每隔6 d调查1次,每次随机选择300个叶片,调查每片叶子上的病斑个数.
2011年7月初进行田间调查,7月14日调查到甜瓜霜霉病发生初侵染的情况,7月20日调查到甜瓜霜霉病发生一次再侵染后的发病情况.共调查4个品种,每品种各调查300片叶子,统计每片叶上的病斑个数.调查地点及侵染情况见表1.
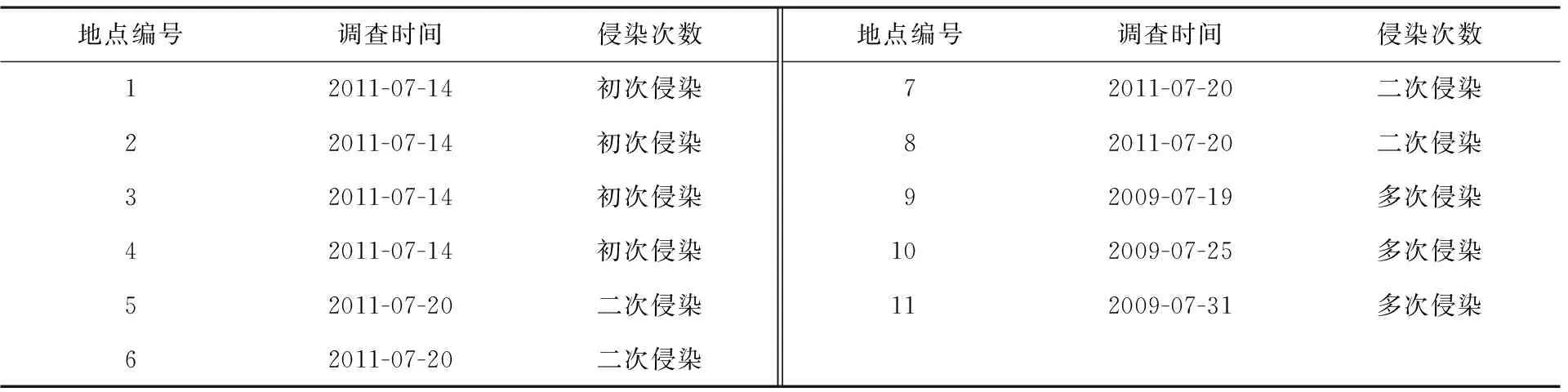
表1 调查地点及侵染情况
病害的空间分布格局采用扩散系数和聚集指数两个空间分布型指标及平均拥挤度和均值的回归关系进行研究.数据处理采用VBA语言编写的相关程序进行[18].
扩散系数是检验种群是否随机分布的一个指数,其公式为
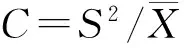
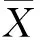
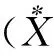
平均拥挤度表示每个个体在一个样本中的平均他个体数(或称邻居数),指的是平均在一个样本内每个个体的拥挤程度.在集团很少,“0”样本很多时,虽然平均数很小,但实际上集团中的个体间仍极拥挤,种内竞争激烈,因此,“平均数”难以反映这种效应.而“平均拥挤度”则可以比较真实地反映出种内竞争等生物因素的作用.
平均拥挤度的计算公式为
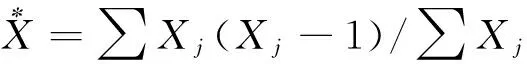
式中Xj为第j个样本的个体数.
1.2 理论抽样数的确定
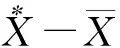
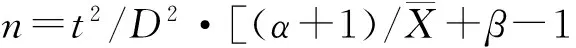
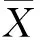
1.3 序贯抽样分析模型和序贯抽样检索表
甜瓜霜霉病的序贯抽样分析模型和序贯抽样检索表利用下式来确定停止线的上、下限:
T(高/低)=NX±t·(N(α+1)X+N(β-1)X2)1/2.
式中:T为调查叶片的累计病斑数;N为抽样叶片数;X为防治指标(每叶病斑定为0.1);t=1.96(保证可靠概率95%条件下的正态离差值);α,β为平均拥挤度和均值回归式中的参数.
2 结果与分析
2.1 甜瓜霜霉病的空间分布格局
2.1.1 扩散系数测定
扩散系数法的测定结果见表2.
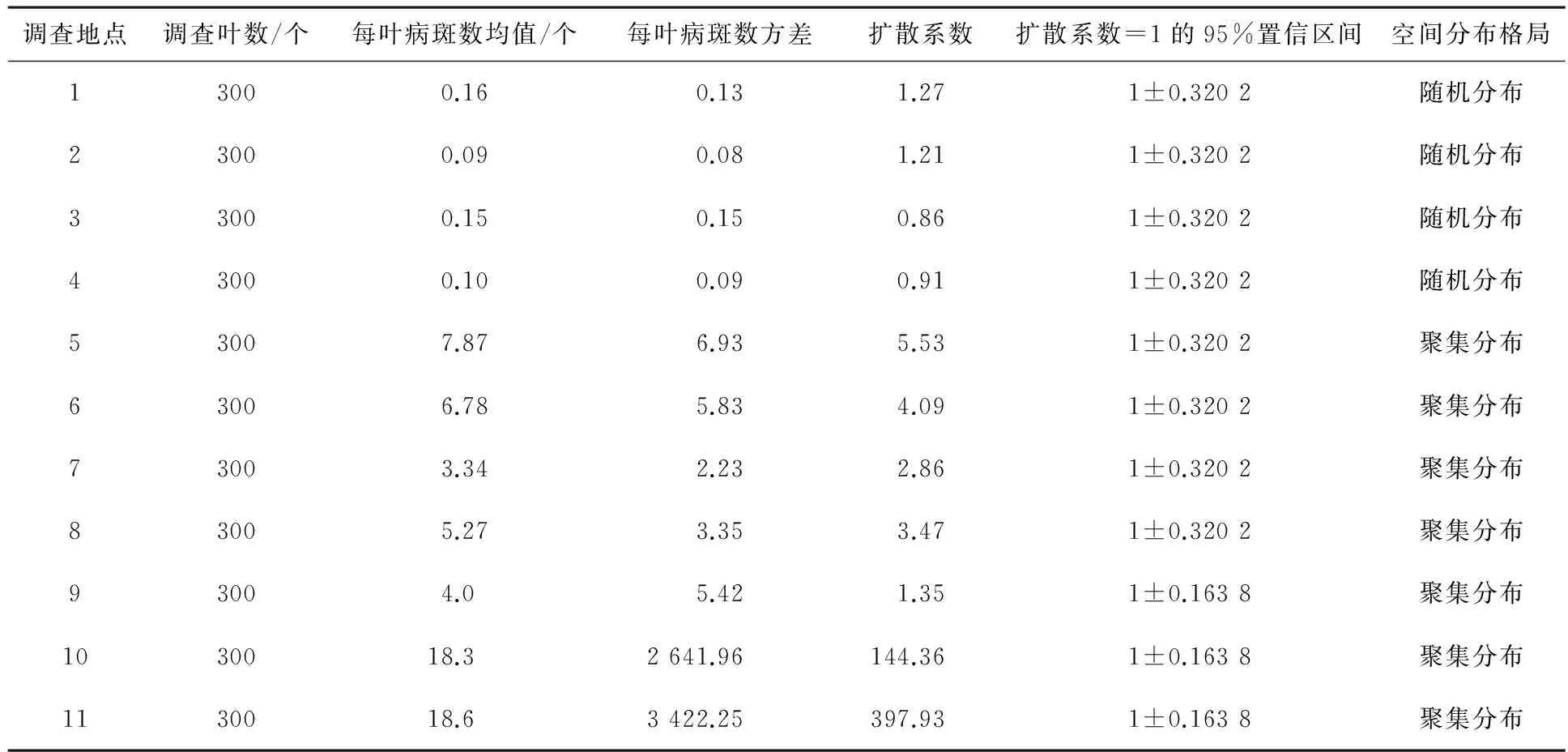
表2 扩散系数法判断病斑在叶片上的空间分布格局
由表2可见,甜瓜霜霉病初侵染后的病斑在叶片上的空间分布格局为随机分布,发生一次或多次再侵染后的病斑在叶片上呈现集聚分布(扩散系数显著大于1).
2.1.2 聚集指数测定
用聚块性指标法测定聚集指数,结果见表3.
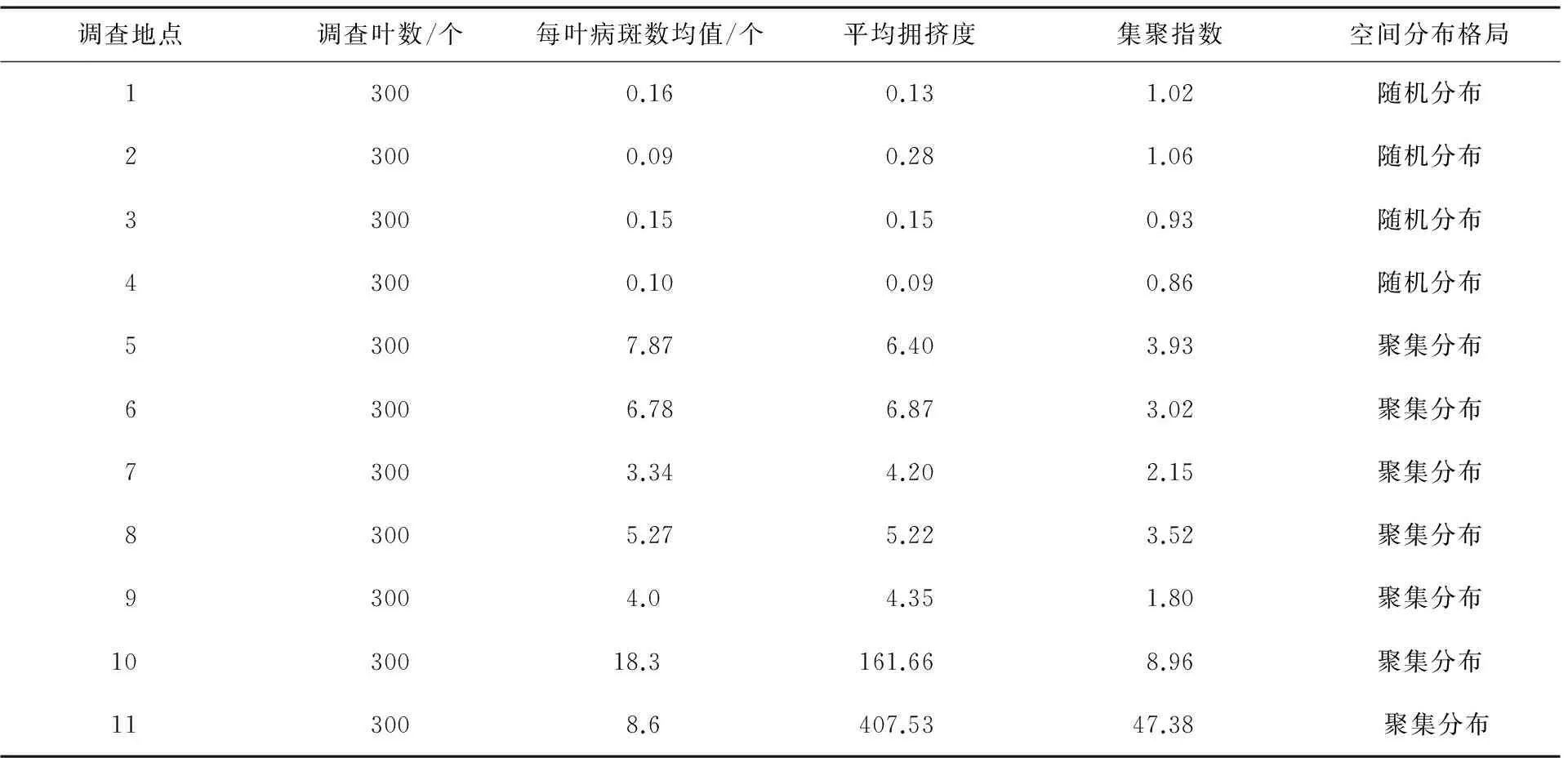
表3 聚块性指标法判断甜瓜霜霉病病斑在叶片上的空间分布格局
由表3可见,用聚块性指标法测定聚集指数判断甜瓜霜霉病初侵染后的病斑在叶片上的空间分布格局为随机分布,发生一次或多次再侵染后的病斑在叶片上的空间分布格局为聚集分布.
2.2 甜瓜霜霉病理论抽样数的计算
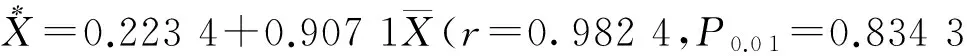
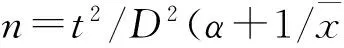
由表4可见,在常见的发病条件下,每个叶片上的病斑数越少,需要调查的叶片数就越多.为保证精度,每百叶累计病斑数5~10个,大约需要随机调查4 600~9 400个叶片,即使病斑数达到50~100个,仍然需要调查500~900个以上的叶片.在粗略的田间调查中,每百个叶片累计病斑数为5~10个,大约需要随机调查500~1 000个叶片,病斑数达到50个时需要调查100个左右的叶片.
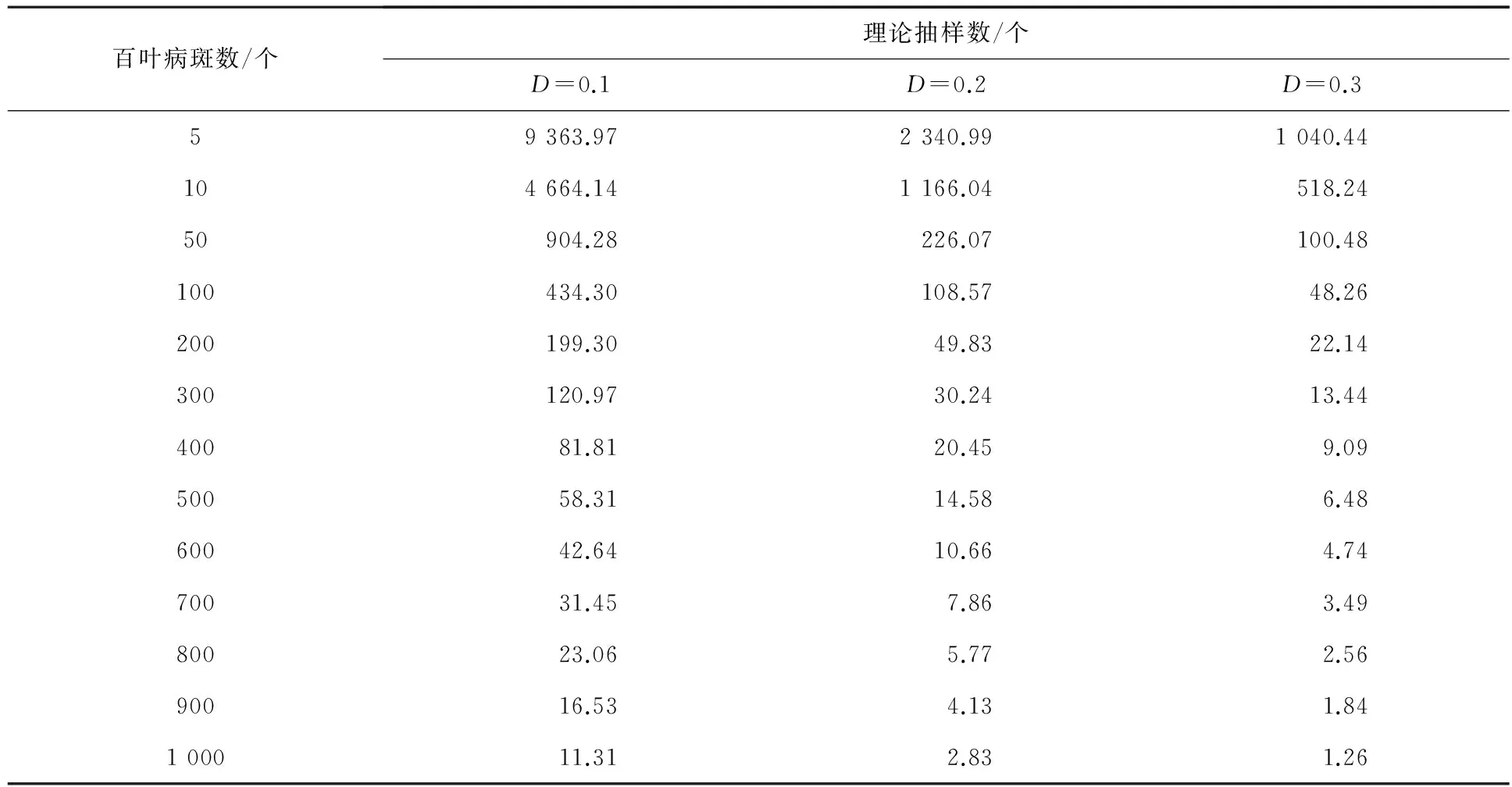
表4 甜瓜霜霉病不同密度理论抽样数值
2.3 序贯抽样分析模型和序贯抽样检索表
序贯抽样是根据田间调查实况,在一定的置信范围内利用取得的样本信息确定合适的抽样量或是否达到防治的指标.根据经验确定防治指标为单叶病斑数x=0.1;将t=1.96,α=0.223 4,β=0.907 1代入序贯抽样公式,得序贯抽样分析模型T(高/低)=0.1N±0.682N1/2,按此模型制作出甜瓜霜霉病序贯抽样检索表(见表5).
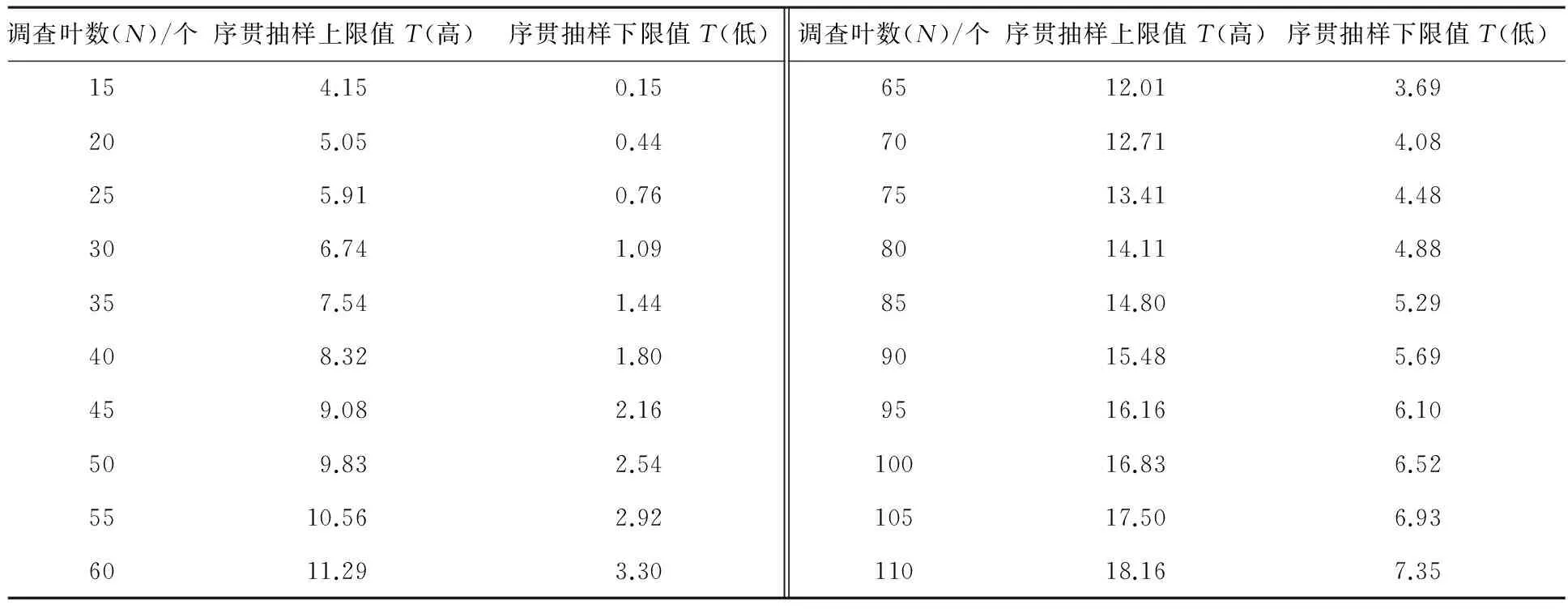
表5 甜瓜霜霉病序贯抽样检索表
根据表5,若被调查的甜瓜叶片上累计病斑数超过上限则可确定为需防治田圃;未达到下限时,可确定为不需防治田圃;若甜瓜叶片上累计病斑数在上下限之间,则应继续调查.
3 讨论
(1) 关于甜瓜霜霉病斑在叶片上空间分布格局及抽样技术的研究,目前国内尚未见报道.我们采用空间分布格局指标法,对调查资料分别进行下列计算:扩散系数、聚块性指标、平均拥挤度和均值的回归关系,确定不同密度的理论抽样数及序贯抽样分析模型T(高/低)=0.1N±0.682N1/2.按此模型制作出甜瓜霜霉病序贯抽样检索表,对霜霉病的调查防治提供了理论依据.
(2) 经过研究证实,甜瓜霜霉病初侵染刚发生后的病斑在叶片上的空间分布格局为随机分布,过了一个潜育期以及多次侵染后,病斑在叶片上的空间分布格局是聚集分布.分析其原因可能在于初侵染时,病原菌孢子囊经空中飞散落入田间时是随机的,因此刚发病时呈随机分布状态;再侵染时游动孢子在初侵染病斑附近侵染萌发概率较大,因此形成了聚集分布状态.
与国内原来关于霜霉病及叶斑病的空间分布型的研究相比,以前的研究田间调查的时间多为病害已经达到盛发期,因此研究结论为病害的空间分布为聚集分布而忽视了病害发生初期可能存在随机分布的情况.本次研究在2011年7月初—7月14日经过连续调查,确切观察到甜瓜霜霉病发生初侵染和发生首次再侵染后的发病情况,从而做出在初侵染发生后病斑在叶片上的空间分布格局为随机分布的结论,这在类似研究中尚不多见.
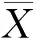
[1] HIURA M,KAWADA S. On the overwintering ofPeronoplasmoparacubensis(B.er C.)Clinton[J]. Japanese Journal of Botany,1933(6):507-513.
[2] 杨渡,白山·哈基塔依,阿地里·亚森,等.干旱区甜瓜霜霉病远距离传播空间结构的初步研究[J].植物病理学报,2007,37(2):192-196.
[3] GULYA T J,M SIREVIC S,THOMAS C E. Preservation of airdried downymildew sporangia in liquid nitrogen without cryoprotectants or controlled freezing[J].Mycological Research,1993,97(2):240-244.
[4] THOMAS C E,INABA T,COHEN Y. Physiological specialization inPseudoperonosporacubensis[J].Phytopathology,1987,77:1621-1624.
[5] 石延霞,李宝聚,刘学敏,等.黄瓜霜霉病菌致病作用与两种细胞壁降解酶关系初探[J].园艺学报,2003,30 (4):465-466.
[6] 骆桂芬,崔俊涛,张莉,等.东北霜霉菌Peronosporamanschurica(Naum) Syd对黄瓜霜霉病的诱导免役作用[J].植物病理学报,1996,26(4):359-364.
[7] 石延霞,李宝聚,刘学敏.高温诱导黄瓜抗霜霉病机理[J].应用生态学报,2007,18(2):389-394.
[8] 余晔,杜金萍,杜相革,等. 硅对黄瓜霜霉病抑制效果和抗性相关酶活性的影响[J].植物保护学报,2010,37(1):36-41.
[9] 王岩,冯明鸣,刘鹏飞,等.黄瓜霜霉病菌对烯肟菌醋敏感性及其抗药性突变体生物学性状研究[J].植物病理学报,2005,35(6):111-112.
[10] 马志强,张小风,韩秀英,等.黄瓜霜霉病菌对甲霜灵的抗药性治理[J].植物保护学报,2005,32(2):223-224.
[11] SEQUEN F C,BACHER J,STAUB J E. Mapping and QTL analysis of horticultural traits in a narrow cross in cucumberusing random amplified polymorphic DNA markers[J].Melecular Breeding,1997(3):257-268.
[12] 张艳菊,秦智伟,周秀艳,等.黄瓜霜霉病菌保存方法[J].植物病理学报,2007,37(4):438-441.
[13] 李宝聚,彭仁,彭靛薇,等.高温调控对黄瓜霜霉病菌侵染的影响[J].生态学报,2001,21(11):1796-1801.
[14] 韩小爽,高苇,傅俊范,等.李宝聚博士诊病手记(二十七)黄瓜霜霉病病原菌的侵染过程、传播途径及防治对策[J].中国蔬菜,2011(9):20-21.
[15] 刘波,朱育菁,肖荣凤,等.西瓜枯萎病病株空间分布格局及抽样技术研究[J].生态学报,2004,24(9):2043~2049.
[16] 段显德,马海霞,杨信东.白菜霜霉病及软腐病空间分布型研究[J].吉林农业大学学报,2010,32(2):130-135.
[17] 田瑞,胡红菊, 王友平,等.梨瘿蚊幼虫的空间分布型及序贯抽样技术[J].华中农业大学学报.2008,27(6):728-731.
[18] 刘影,杨信东,李启云,等.用Excel中的VBA编写生物种群空间分布型指数计算程序[C].全国植保科技创新与发展大会学术论文集.重庆:中国植物保护学会,2008:690-692.
[19] BEALL G,RESCIA R R.A generalization of the Neyman’s contagious distributions[J].Biometrics,1953(9):354-386.
[20] 兰星平.关于Taylor幂法则的讨论[J].林业科学,1996,32(1):86-90.
[21] 沈佐锐. 关于Taylor幂法则的统计学讨论. [J].生态学杂志,1990,9(6):64-67.
(责任编辑:方 林)
Spatial distribution pattern and sampling technologies of melon leaf downy mildew disease spots on the blades
DUAN Xian-de1,DONG Rong-chun1,WANG Shuo2,YANG Xin-dong2
(1.College of Agriculture,Liaodong University,Dandong 118003,China;2.College of Agriculture,Jilin Agricultural University, Changchun 130118,China)
Spatial distribution pattern in leaves of disease spots of melon downy mildew was studied in this paper.The study was conducted through the two spatial distribution pattern indexes of dispersion coefficient and aggregation index as well as the regression relationship of evenness aggregation and mean value. The results showed that the downy mildew spots were distributed randomly in melon leaves after first infection,while it exhibited an aggregated distribution after second infection. With the increase of disease spots,the sampling number needed gradually decreased. sequential sampling model isT(high/low)=0.1N±0.682N1/2,When the number of leaves isN,if the field of the accumulated disease spots beyond the upper threshold is considered the field that should be prevented and treated,if it is under the lower threshold,the one unnecessary to be prevented and treated,if it is between the lower and upper threshold,a continuous survey is due. Used the relativity method based on aggregation index and average data to analyze and judge aggregation degree of disease spots of melon downy mildew in leaves and disease severity,which can completely replace Taylor power law or other relativity methods to judge aggregation intensity and population density.
melon downy mildew;spatial distribution pattern;optimum sampling number;sequential sampling search table
1000-1832(2015)04-0123-06
10.16163/j.cnki.22-1123/n.2015.04.026
2015-01-05
国家自然科学基金资助项目(30600003);辽东学院博士启动基金资助项目(891101);丹东市科技发展计划项目(20130726).
段显德(1964—),男,博士,副教授,主要从事植物病理学研究.
S 432.1 [学科代码] 210·6035
A

