计数问题中的转化与构造

☉湖北省天门中学郑月姣

计数问题中的转化与构造

☉湖北省天门中学郑月姣

计数问题是高考考查的一个基本问题，问题呈现方式多样，较难入手·如何让看似“杂乱无章”的问题“有章可循”，笔者想以转化与构造的思路探讨一下，下面举例说明·

例1求满足下列条件的集合M的个数·

（1）｛1｝⊆M⊆｛1，2，3｝；

（2）｛1，2，3｝⊆M⊆｛1，2，3，4，5，6，7，8，9，10｝；

（3）｛a1，a2，…，am｝⊆M⊆｛a1，a2，…，an｝（n＞m，n，m∈N*）·

解析：（1）列举法可解决·符合条件的集合M为：

｛1｝，｛1，2｝，｛1，3｝，｛1，2，3｝，共4个·

第（2）、（3）小题、就不适合用列举法了·观察（1）中的规律：

设A=｛1｝，B=｛1，2，3｝，CBA=｛2，3｝·

CBA的子集为Ø，｛2｝，｛3｝，｛2，3｝·

集合M为A与CBA的某一个子集的并集·

所以集合M的个数等于CBA的子集的个数，求集合M的个数转化为求CBA的子集的个数·而含n个元素的集合的子集为2n个·

所以（1）中符合条件的集合M的个数为22=4（个）·

（2）中符合条件的集合M的个数为210-3=128（个）·

（3）符合条件的集合M的个数为2n-m（个）·

例2（1）已知集合A，B满足A∪B=｛1，2｝，则满足条件的集合A，B有多少对？

（2）已知集合A，B满A∪B=｛1，2，3，4，5，6，7，8，9，10｝，则满足条件的集合A，B有多少对？

（3）已知集合A，B满足A∪B=｛1，2，…，n｝，则满足条件的集合A，B有多少对？

解析：（1）可以由列举法解决·

A Ø｛1｝｛1｝｛2｝｛2｝｛1，2｝｛1，2｝｛1，2｝｛1，2｝B｛1，2｝｛2｝｛1，2｝｛1｝｛1，2｝Ø｛1｝｛2｝｛1，2｝

共9对·

（2）、（3）列举法就不适用了·

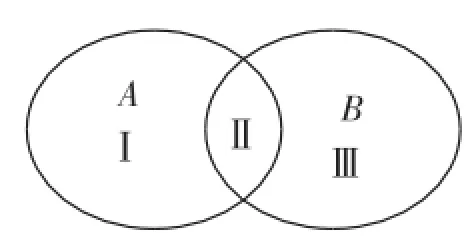
图1

对于（1）可作如下的转化·将1、2两个数字填入图1中的Ⅰ、Ⅱ、Ⅲ三个区域内，每个数字必须且只需填一个区域，按照这种方法，每一个方案就对应着一对集合A、B，而由排列组合的有关知识，不同的方案有3×3=32种·所以，满足条件的集合A，B有32= 9对·

此法对于（2）、（3）也适用·所以问题（2）中有310对·问题③中有3n对·

例3设集合Pn=｛1，2，…，n｝，n∈N*，记f（n）为同时满足下列集合A的个数：①A⊆Pn；②若x∈A，则2x∉A；③若x∈CPnA，则2x∉CPnA·

（1）求f（4）；

（2）求f（n）的解析式（用n表示）·

解析：（1）P4=｛1，2，3，4｝，符合条件的集合可以由列举法解决·｛2｝，｛1，4｝，｛2，3｝，｛1，3，4｝·

（2）不能由列举法解决，分析（1）中集合A中的元素，由条件①②③知：当1∈A时，2∉A，2∈CP4A，4∉CP4A，4∈A；当1∉A时，1∈CP4A，2∉CP4A，2∈A，4∉A，4∈CP4A·

故2、4两个偶数是否属于A，由1是否属于A确定，而1、3无限制条件，既可以属于A，也可以不属于A·因此，集合A的个数即等于｛1，3｝的子集的个数f（4）=22=4个·对于（2）任取偶数x∈Pn··

设x=m·2k，k∈N*，m为奇数·由条件①②③知：

若m∈A时，x∈A⇔k为偶数；

若m∈A时，x∉A⇔k为奇数·

所以，x是否属于A由奇数m是否属于A确定·集合A中的元素只要确定Pn中每一个奇数是否属于A，相应的偶数也可以随之确定，设Qn为Pn中所有奇数组成的集合，Qn的子集个数即等于集合A的个数·当n为奇数时，Pn中有

小结：（1）综上所述，将所要解决的问题记为集合A，要确定A中元素的个数却难于直接确定，可以构造一个与之一一对应的集合B，而集合B中的元素个数方便计数，B中的元素个数等于A中的元素个数·

（2）在由具体到抽象的探讨中，从具体问题出发，力争找出问题的实质，寻求通解通法，由浅入深，由表及里，训练学生研究性的思维品质，这是教学中应大力提倡的·

1·杜志建·2009～2013新高考五年汇编·数学（理科）［J］·乌鲁木齐：新疆青少年出版社，2014·F