一道定值问题的另解、背景及变形

☉江苏省如皋市薛窑中学夏俊梅

一道定值问题的另解、背景及变形

☉江苏省如皋市薛窑中学夏俊梅

《数学通报》2009年第3期刊出的问题1783（以下简称题1）是：设M是定圆O外一个定点，试问：在定圆O内是否存在一个定点N，使得对于定圆O上的任意点P，比值为定值？若存在，求出该定点N；若不存在，请说明理由·

笔者觅得此题不同于供题者的另一种解法，这种解法与供题者的解法相比，显得较为笨拙，但这种解法却能揭示定点N的一个有趣性质·当然，该题也有古老的历史背景，从而我们可变形出许多与该题同样精彩的其他问题·

一、另解

首先证明一个命题·

命题：设M（m，0）是不在圆O：x2+y2=a2上且不与O重合的一个定点，过M作不与x轴垂直的一动直线与圆O交于两点A、B，取A关于x轴的对称点C，则直线BC必过定

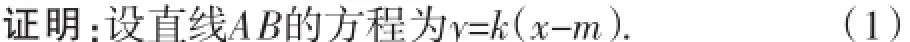
设A（x1，y1）、B（x2，y2），则由（2）得：

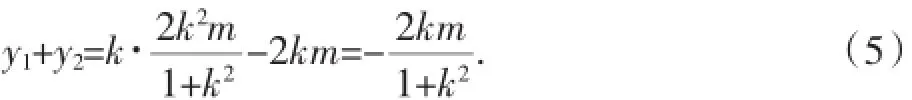
同样由（1）可知：x1y2+x2y1=x1［k（x2-m）］+x2［k（x1-m）］=2kx1x2-km（x1+x2）·

由（1）可知y1+y2=k（x1+x2）-2km，将（3）代入，得：

再将（3）、（4）代入上式，得x1y2+x2y1=2k·

由题意得直线BC的方程为：

现在解题1·

解：过M、O两点作直线与圆O交于A、B两点，如图所示·过M作圆O的一条切线，切点为P′·然后过P′作MO的垂线，垂足为N，则定点N即为所求·

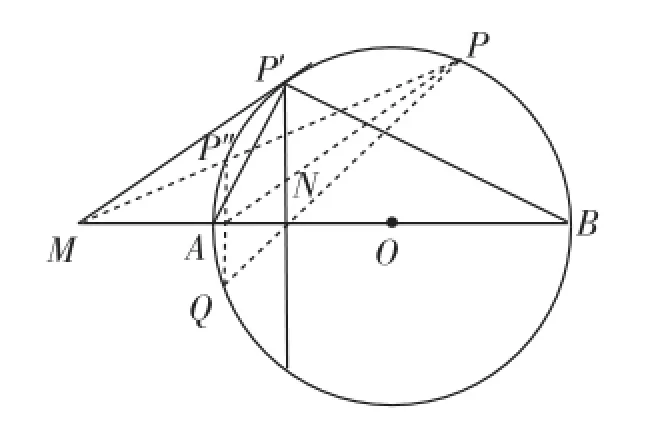
连接P′A，则P′A为∠MP′N的平分线·

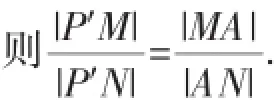
连接P′B，则P′B是△P′MN的外角平分线，也有：

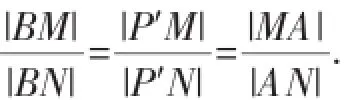
过M作圆O的任一条不与AB重合的割线MP′′P，如图，作P′′关于直线AB的对称点Q，连接PQ、PA，则由命题PQ必过直线AB上一定点N′，N′必满足|ON′|·|OM|=|OA|2，而N点满足|ON|·|OM|=|OA|2，则N与N′重合·

至此，我们得到求N点的不同于供题者的另一种解法·这种方法比供题者的方法易于操作·另外，我们还获得N点如命题揭示的一个性质·

二、背景

历史上有这样一道题：设一动点至两定点的距离之比是一个不为零的常数，求这个动点的轨迹·

此题以下简称题2，见文1·

若常数为1，则动点的轨迹是以两定点为端点的线段的垂直平分线；若常数不为1，则取这两定点关于此比值的内比分点及外比分点，再以这两点为直径作圆，符合条件的动点的轨迹就是这个圆·

这个圆叫做阿波罗尼斯（Apollonius，约公元前260～200年）圆·

供题者提供的解答也并非“原创”，与文1中题2的解答完全相同·

若我们利用阿波罗尼斯圆的性质，则题1的解答更为简洁·

知道了题1的背景，我们可让M更“自由”一些，不一定在圆O外部，M在圆O内部且不与O重合，也有类似结论，故题1可改为题1′·

题1′：设M是不在定圆O上，也不与O点重合的一个定点·试问：是否存在一个定点N，使得对于定圆O上的任意点P，比定值？若存在，求出该定点N；若不存在，请说明理由·

这样找N点要分两种情形·若M在圆O外部，上文已给出找N点的方法；若M在圆O内部，作MP′⊥MO与圆O交于P′，过P′作圆O的切线，与直线MO交于N点，则点N为所求·以下解法与上文提供的方法无异·

如果按射影几何的理论，题1及题1′实质上是已知三点，求第四点，使这四点成调和比·故题1及题1′有如下简解·

连接MO与圆O交于A、B，则使（AB，MN）=1的N点即为所求·

三、变形

有了上文的准备，我们可随心所欲地对题1进行改编、变形·

题3：设A、B为两个定点，D是线段AB上不与端点重合的一个定点，求动点C的轨迹，使CD恒为△CAB的内角C的平分线·

题4：设A、B为两个定点，D为线段AB的延长线上一个定点，求动点C的轨迹，使CD恒为△CAB的内角C的外角平分线·

题5：设直线l是经过定圆圆心的一条直线，试问：在直线l上能否找到两个定点M、N，使得对于定圆上的任意一点P，恒有比值2？若存在，求出这两个定点M、 N；若不存在，请说明理由·

题6：设直线l是经过定圆圆心的一条定直线，试问：在直线l上能否找到两个定点M、N，使得对于定圆上任一点P，恒有=k（k为常数）？若存在，求出这两个定点M、N；若不存在，请说明理由·

题7：设直线l是与定椭圆的长轴重合的一条直线，试问：在直线l上能否找到两个定点M、N，使得对于定椭圆上的任一点P，恒有=k（k为常数）？若存在，求出这两个定点M、N；若不存在，请说明理由·

题8：M是圆O外一点，线段MO与圆O交于一点P，过M作圆O一条不过圆心的割线，与圆O交于A、B，AC⊥MO，与圆O交于另一点C，BC与MO交于N，设D是圆O上不与MO共线的一点·求证：DP是∠MDN的平分线·

1·梁绍鸿·初等几何［M］·北京：人民教育出版社，1980·A