有关“定点”问题的探究

☉内蒙古赤峰市赤峰二中孙广仁

有关“定点”问题的探究

☉内蒙古赤峰市赤峰二中孙广仁

有关“定点”问题在近几年的高考试题中频繁出现·本文将结合例题围绕有关“定点”问题展开，以飨读者·

一、探究直线过“定点”问题

例1（2009年高考江苏第18题）在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y-1）2=4和圆C2：（x-4）2+（y-5）2= 4·

（1）若直线l过点A（4，0），且被圆C1截得的弦长为，求直线l的方程；

（2）设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，试求所有满足条件的点P的坐标·

解：（1）略·

（2）设点P的坐标为（m，n），直线l1、l2的方程分别为：

因为直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，两圆半径相等，由垂径定理，得圆心C1到直线l1的距离与圆心C2到直线l2的距离相等·

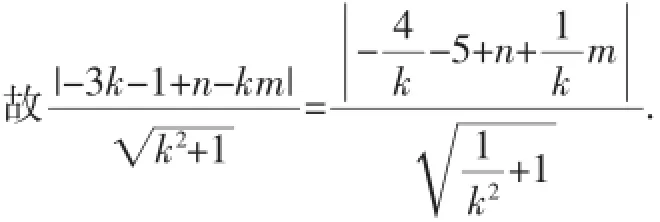
化简得：（2-m-n）k=m-n-3或（m-n+8）k=m+n-5·

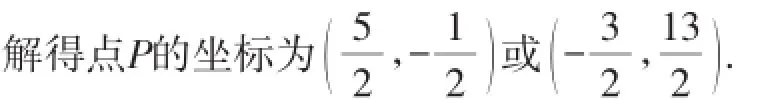
点评：本题实际上是探究两条直线过同一“定点”问题，由于“过点P有无穷多对互相垂直的直线l1和l2”，注意到直线l1和l2的斜率是变化的，为此我们可以选择l1的斜率k为变量·因为两圆的半径相等，由垂径定理得到圆心C1到直线l1的距离与圆心C2到直线l2的距离相等，从而得到关于k的方程（2-m-n）k=m-n-3或（m-n+8）k=m+n-5有无穷多解，亦即与k无关·

变式：（2010年高考江苏第18题）在平面直角坐标系xOy中，如图，已知点为A、B，右焦点为F，设过点T（t，m）的直线TA、TB与椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0·

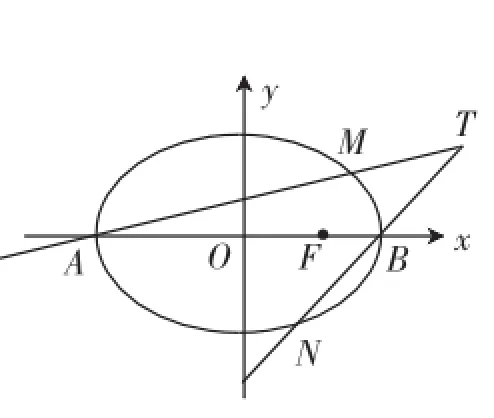
（1）设动点P满足|PF|2-|PB|2=4，求点P的轨迹；（2）设x=2，x=，求点T的坐标；12

（3）设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）·

点评：考生普遍反映第三问计算量大·因为涉及的动点T（9，m）的纵坐标m的不确定性，所以要求的定点肯定与m的值无关·不妨先研究特殊情况，当直线MN与x轴垂直时，过x轴上的定点D（1，0），然后研究一般情况下直线MN过点D（1，0），这里又有两条途径：一是求出直线MN的方程，令y=0，解得x=1；二是运用kDM=kND证明M、N、D三点共线·

二、探究圆过“定点”问题

例2在平面直角坐标系xOy中，已知抛物线y2=2px上横坐标为4的点到该抛物线的焦点的距离为5·

（1）求抛物线的标准方程；

（2）设点C是抛物线上的动点，若以C为圆心的圆在y轴上截得的弦长为4，求证：圆C过定点·

变式：已知圆O：x2+y2=1，直线l1过点A（3，0），且与圆O相切·

（1）求直线l1的方程·

（2）设圆O与x轴相交于P、Q两点，M是圆O上异于P、Q的任意一点，过点A且与x轴垂直的直线为l2，直线PM交直线l2于点P′，直线QM交直线l2于点Q′·求证：以P′Q′为直径的圆C总经过定点，并求出定点的坐标·

点评：因为M是圆O上异于P、Q的动点，所以直线PM的斜率是变化的·故本题处理的方法有两种：一是设动点M（x0，y0），由圆C的方程与x0、y0无关，确定定点；二是设直线PM的斜率k，由圆C的方程与k无关，令y=0，求出定点·

三、探究平面内存在定点问题

例3已知⊙O：x2+y2=1和点M（4，2）·

（1）过点M向⊙O引切线l，求直线l的方程·

（2）求以点M为圆心，且被直线y=2x-1截得的弦长为4的⊙M的方程·

（3）设P为（2）中⊙M上任一点，过点P向⊙O引切线，切点为Q·试探究：平面内是否存在一定点R，使得|PQ| |PR|为定值？若存在，请举出一例，并指出相应的定值；若不存在，请说明理由·

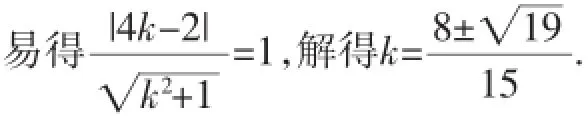
所以⊙M的方程为（x-4）2+（y-2）2=9·

（3）假设存在这样的点R（a，b），点P的坐标为（x，y），相应的定值为λ·

（1）求圆C的方程·

（2）若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长·

点评：对于第三问，设P（s，t），G（x0，y0），和点G在圆C上，得两个关于x0、y0的方程，联立可得一个关于x0、y0的方程，比较系数，得到点P的坐标为（4，0）·

总之，处理有关“定点”问题，要注意动与静的转化，确定好谁为变量，加深对概念本质的理解，培养思维的深刻性·同时也要对动与静的关系仔细观察，便于寻求规律，培养思维的灵活性与广阔性·A