重视反思，培养学生的数学思维能力

☉江苏省张家港市乐余高级中学张森焱

重视反思，培养学生的数学思维能力

☉江苏省张家港市乐余高级中学张森焱

学生若能在课前预习、课堂教学或者课后完成作业的基础上，主动反思成功的经验，总结失败的教训，概括自己所学及其所应用的数学思想方法，那么一定会达到培养自身数学思维能力的目的·本文中笔者将结合课堂教学实例，从三个方面来探讨学生数学思维能力的培养·

一、重视对书本例题、课后习题的反思

高考数学试题越来越重视对以思维能力为核心的数学能力的考查·命题“来源于课本，又高于课本，是课本的创新”的趋势越来越明显，即命题不再是课本例题、课后习题的简单再现，而是取于课本，加以变式得到·这就要求教师在平时的数学教学中，对课本中的例题、课后习题不能停留在照搬照用上，而应以课本中的例题、习题为依据，精心设计问题串，引导探索发现，展现形成过程，从而达到既适应高考又培养学生数学思维能力的目的·

在苏教版必修2立体几何教学部分有这样一道习题（书本第71页）：设P、A、B、C是球O表面上的四个点，PA、PB、PC两两垂直，且PA=PB=PC=1m，求球的体积和表面积·

笔者执教的是乡镇上一所三星级普通高中，初次接触这个题目，学生在处理上都出现了很大问题·作为教师，不妨先降低题目的难度，在解决书本上这道习题之前我们可以先引入这样的一个问题：已知长方体的长、宽、高分别为1、2、3，求此长方体外接球的表面积·

评析：在教学中我们通过实物展示和电子白板再现让学生发现长方体的体对角线的长度即为球体的直径，积S=4πR2=14π.

引申：在上述例题讲解的基础上，教师可以引导学生反思长方体的长、宽、高与其外接球的直径的关系·通过教学过程中的实物展示，学生发现若长方体的长、宽、高分别为a、b、c，则其外接球的直径为其体对角线的长，

有了本题作为突破口，我们再来解决书本上的这道例题·虽然在本题中我们看不到长方体的影子，但是同学们可以想象PA、PB、PC两两垂直，即从同一个点出发有三条线相互垂直，有点像我们平时生活中遇到的什么问题？同学们会联系到我们立体几何中常说的“墙角”问题，于是构造长方体就产生了·

《普通高中数学课程标准（实验）》提出“应提高数学地提出、分析和解决问题（包括简单的实际问题）的能力·”笔者以上面的两个问题为契机，引出了下面的练习：已知正四面体的棱长为求其外接球的体积·

事实上，学生经过总结反思发现这三个题目是同一个类型·在教学中，教师可以从书本上的例题、课后习题出发，以问题串的形式，不断引导学生进行积极的思维活动·在解决问题过程中，通过观察、发现、归纳、类比、猜想、推理、证明等一系列数学活动来培养学生的数学思维能力·

二、重视对解题教学的反思

1·反思解题方法

在数学解题教学中，不同的数学问题存在不同的解决方法·教师应适当地引导学生反思解决问题的方法·对解题方法的反思，其教学价值不是单纯让学生知道如何解出这个数学题，而是督促学生站在不同的视角、用不同的方法去思考、去审视、去理解这个题目，从而开阔学生的思路，培养学生的数学思维能力·

在高二“圆锥曲线与方程”教学中笔者曾经执教过这样一个例题：已知A（-2，0）、B（2，0），动点M（x，y）满足则动点M的轨迹是什么？

第一次接触这个题目，在教学中笔者发现很多学生第一思路是通过移项、完全平方解决，这时教师不要立刻制止学生的做法·等学生的做法结束后，教师可以慢慢引导学生观察经过移项、两边完全平方最终算出动点的轨迹是以（-2，0）、（2，0）为焦点，2a=6的椭圆·做到这里，教师不妨反问一下学生：大家现在反思一下刚才的解题方法，发现了什么？这个解决的过程有点类似什么的解决方法？哦！学生此时才明白，努力了半天的化简过程就相当于把椭圆方程又推导了一遍·教师追问：我们能否直接用椭圆的定义进行解决呢？经过观察我们发现定点（-2，0）、（2，0）的距离和，式子右边是定值6·于是顺理成章地就又回到了椭圆的定义上：平面内到两个定点的距离和为定长（2a＞2c）的点的轨迹是椭圆·于是可以根（-2，0）、（2，0），定值为2a=6，从而得出椭圆的标准方程·

在解题教学中，教师要努力培养学生的主动精神，要先给学生提供独立“攻坚”的机会，教师要“延迟判断”，在学生尝试、探索的过程中允许他犯错误·缺乏经验的教师通常认为需要克服困难的地方是学生容易犯错误的地方，因此，常常在学生犯错误之前就提醒学生加以注意，甚至直接给学生正确的示范·事实上，学生自己思考出来的结果，往往是应用策略多种多样，有的甚至比已知应用的策略好得多·教师要转变“讲得越多、越细，学生就掌握得越好”的师本位的观念为学生自主地进行积极探索和尝试的生本位的观念，这样学生可能获得对思维策略的更深刻理解和认识·

2.对解题结果的再反思

学习数学不仅要在理解的基础上掌握知识，还要学会应用所学知识解决问题，更要养成数学地看待问题的习惯·G·波利亚在“怎样解题表”中将解题过程分为弄清问题、拟订计划、实施计划、解后回顾四个步骤·一般在解题教学中教师偏重于“审题（即弄清问题）”这一步骤，对解后的回顾与反思做的较少·事实上，解题后的回顾与反思，一方面可以检验解题过程和结果，另一方面可以对解题思路进一步整理、归纳、引申、发散，既有助于学生对数学知识的融会贯通，更有利于学生数学思维品质的培养·笔者仍以例题“已知A（-2，0）、B（2，0），动点迹是什么？”做研究·

教师在引导学生观察可将代数方程语言转化为几何语言后，可以继续启发学生思考：若修改条件，轨迹又是什么？

方案1：6改成4，轨迹又是什么？

方案2：4改成3，轨迹又是什么？

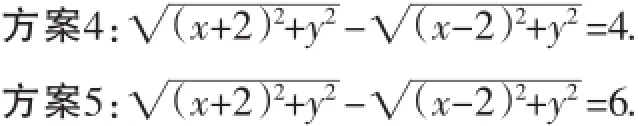
这些方案的一一引出，可以加深学生对圆锥曲线的定义的认识·通过对一系列问题的探究，深化对数学问题的理解，培养思维品质的深刻性、创造性、科学性和批判性，提高了学生的想象力及分析、解决问题的能力·通过对问题的不断引申，精心设问，引导学生学习解题的一般方法及联想、类比、猜测、证明和合情推理等方法·

三、重视对错题的反思

在教学中，我们不难发现对同一种类型的数学问题，即使做了多次后，学生还是经常出错·究其原因，学生习惯于做完题就了事，并不会主动考虑在应用数学知识解决这类问题时，对解题方法、解题中反映出的数学思想作深刻的再认识，即没有反思的习惯·笔者在执教“基本不等式及其应用”这节内容时曾让学生到黑板上展示这样的两道课堂练习的错误解法·

在学生展示错误的基础上，教师可以引导学生自查自纠，反思错在哪里·通过小组间合作讨论，从而总结出错误原因，即用基本不等式求最值必须具备三个条件：一“正”、二“定”、三“相等”·对于展示1，因为0＜x＜1，故lnx＜0，所以不满足基本不等式求最值的第一个条件“正”，解决本题必须“变负为正”·对于展示2，事实上t=中的新元“t”是有范围的，即t≥2·注意这一细节之后发现用基本不等式求最值的第三个条件：三“相等”中的等号是取不到的，那么展示2的最值只能通过函数的单调性来解决了·

在解题教学中，教师对学生出现的错误解法未必每次都要及时指出，教师可以从学生错误的地方入手展开教学，在认知冲突中加深学生的印象，从而培养学生的数学思维能力·A