基于灰色(1,1)模型的近场源高阶特征估计

李瑞斋， 李义华

(1.郑州大学 西亚斯国际学院，文理学院，河南 新郑 451100;2.河南大学 计算机与信息工程学院，河南 开封 475000)



基于灰色(1,1)模型的近场源高阶特征估计

李瑞斋1*， 李义华2

(1.郑州大学 西亚斯国际学院，文理学院，河南 新郑 451100;2.河南大学 计算机与信息工程学院，河南 开封 475000)

近场源的高阶特征参数估计是阵列信号处理的重要内容.通过对近场源高阶特征参量估计可以实现对波达方向(DOA)的频率估计、时延估计、运动目标的多普勒估计.传统的近场源特征估计算法采用单频特征估计方法，无法实现对信号各个参量的联合估计.该文提出一种基于灰色(1,1)模型的近场源高阶特征估计算法.构建近场源的参量估计数学模型，通过空间谱估计方法，实现对空间信息的获取，利用信号子空间和噪声子空间的正交性，通过改变灰色(1,1)数学模型来减少对高阶特征参量不平衡敏感性，实现高阶参量联合特征估计.仿真结果表明，采用该算法进行近场源的高阶特征参量估计，能较精确的估计出两个信源的方位角、距离和频率三维参数，在雷达、声纳、通信等信号与信息处理中展示了较好的应用价值.

近场源；参量估计；灰色(1,1)模型

近年来，随着计算数学和应用数学的快速发展，基于数学分析和数学模型构建的信号处理方法广泛应用在阵列信号处理中.近场源的信号处理作为阵列信号处理的主要研究内容，跟随雷达、声纳、通信等信号与信息处理技术的发展而受到了人们的广泛关注.近场源是相对于远场的概念，在波达方向(Direction of Arrival，简称DOA)估计过程中，相对于阵列孔径处于远场，当信源靠近阵列而落入近场阵列孔径的空间信源部分为近场源.近场源的高阶特征参数估计是阵列信号处理的重要内容.通过对近场源高阶特征参量估计可以实现对波达方向(DOA)的频率估计、时延估计、运动目标的多普勒估计.研究近场源高阶特征估计算法受到人们重视[1～3].

传统方法中，对近场源的高阶估计方法通过信源的距离及其DOA来联合确定，采用高阶微分方程和微分处理方法，通过构建非线性高阶微分方程，进行小迟滞稳定解渐进分析，进行近场源的距离和DOA的二维参数估计.近场源的信号模型中包含着大量的高阶特征信息，通过高阶特征参量估计，利用高阶累积量与二阶统计量相比的非高斯信息和幅度平稳特征信息，可以提高对近场源的参量估计精度[3].而传统的近场源特征估计算法采用单频特征估计方法，无法实现对信号各个参量的联合估计[4].针对上述问题，本文提出一种基于灰色(1,1)模型的近场源高阶特征估计算法.首先构建近场源的参量估计数学模型，给出模型假设条件，采用高阶累积量算法实现对近场源参量的联合估计，最后进行仿真实验实现性能验证.

1 近场源高阶特征参量估计灰色(1,1)数学模型

1.1 近场源的提出和信号模型设计

近场源是通过空间谱估计方法，实现对空间信息的获取，假定有N=2P个均匀线性间距为d的信号接收模型，阵元位置的近场附近有L个近场窄带信号源，得到本文研究的高分辨DOA估近场源模型如图1所示.

设阵列中心处的阵列孔径的菲涅尔(Fresnel)区域坐标为0，以其为相位参考点[5]，则第m个阵列中心的距接收信号可表示为：

(1)

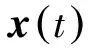
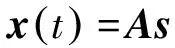
(2)

其中：

(3)

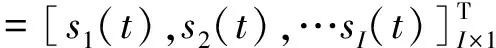
(4)

其中s1(t)为第i个信源的慢变幅度调制函数，pm为阵元m入射信号的统计特性，nm(t)为阵元m上的噪声.

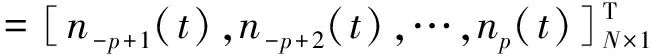
(5)

A=[a(θ1,r1),a(θ2,r2),…,a(θI,rI)]N×I,

(6)

其观察信号表达式为

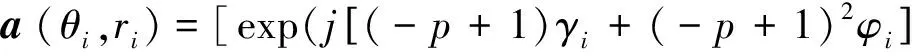
(7)

其中，1≤i≤I，矩阵A的第i列向量a(θi,ri)称为信源i接收到的观测信号.由Fresnel近似得φmi的泰勒级数展开：

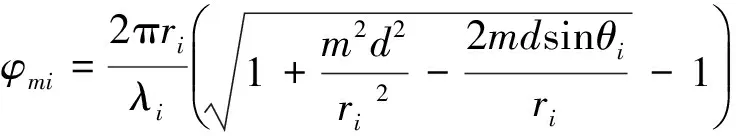
(8)

s(t)=a(t)cos(2πfct+φ(t)),

(9)

其中，si(t)为第i个信源的慢变幅度调制函数，xm(t)为阵元m入射信号的统计特性，nm(t)为阵元m上的噪声.

1.2 灰色(1,1)数学模型及其在高阶特征参量估计中的应用

(10)

(11)

(12)

(13)

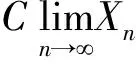
(14)

RxV=ΛV.

(15)

观测信号协方差矩阵为

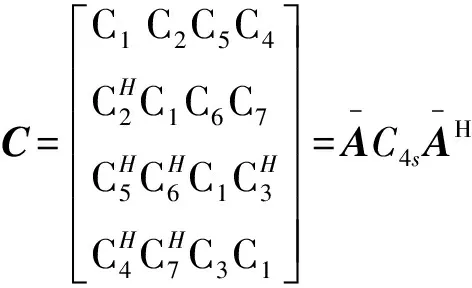
(16)

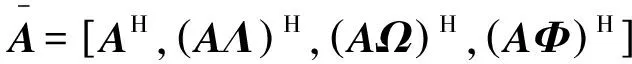
C=EΣEH,

(17)

式中，E=[e1,e2,…,e4P]为由特征值按降序排列组成的对角矩阵；Σ=diag[σ1,σ2,…,σ4P]为特征值组成的对角矩阵，且

σ1>…>σL>σL+1=…=σ4P=0.

(18)

因此可由灰色(1,1)数学模型，得到信号子空间个数估计信源的个数L.

2 近场源高阶特征估计算法改进实现

通过对近场源高阶特征参量估计可以实现对波达方向(DOA)的频率估计、时延估计、运动目标的多普勒估计.传统的近场源特征估计算法采用单频特征估计方法，无法实现对信号各个参量的联合估计.提出一种基于灰色(1,1)模型的近场源高阶特征估计算法.

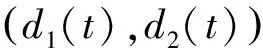
(19)

推导中利用了信号的窄带假设，即si(t)≈si(t+1)，得到不同的信源其距离参数的特征提取方程：

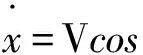
(20)

(21)

(22)

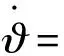
(23)

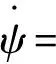
(24)

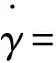
(25)

基于灰色(1,1)数学模型，计算非零特征值及相应的特征矢量，得到近场源的四阶累积量矩阵x的k阶矩为：

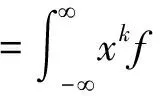
(26)

利用高阶累积量的性质可以推出：

(27)

Ex=E0Γ，Ey=E0Ψ，Ez=E0Υ,

(28)

把信源峰度组成的对角矩阵Es分成四个P×L的矩阵E0,Ex,Ey,Ez，即Es=[e1,e2,…eL]=[E0,Ex,Ey,Ez]H.由此得到基于灰色(1,1)模型的近场源的二维联合估计值为：

[E0,Ex,Ey,Ez]HT=[A,AΛ,AΩ,AΦ]H.

(29)

因此ExT=E0TΛ，EyT=E0TΩ，EzT=E0TΦ.其中，A是一个维数为P×I的矩阵，其第i列矢量可表示为

(30)

Λ=diag[ej2w1,ej2w2,…,ej2wI].

(31)

值得说明的是，由上面的推导，每个近场源的信源的参数自动配对，由此提高对高阶特征参量的估计精度.

3 仿真实验

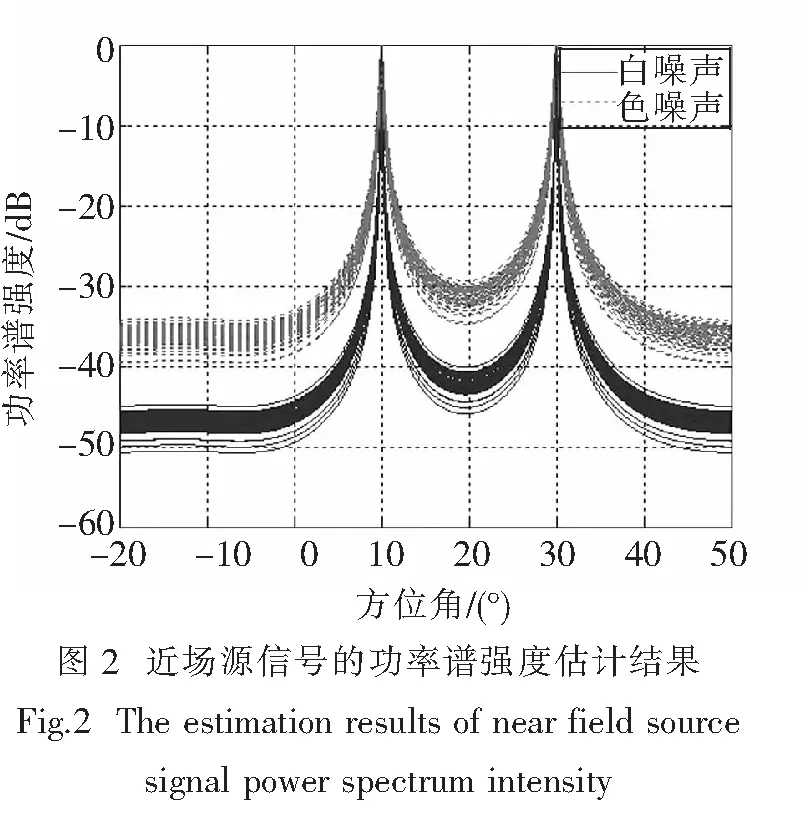
为了验证本文算法在实现近场源高阶特征参量估计性能，进行仿真实验.仿真实验测试的近场源高阶特征参量主要有信源载频、方位角和距离三维参数的预计.实验时，近场源信号为等功率的复指数宽带信号，分别记为s1和s2，信号的频率分别为180 Hz，120 Hz，采样频率为3 000 Hz，信号的方位为10°，30°，噪声分别为高斯白噪声和高斯色噪声，距离分别为0.6λ1，0.2λ2，根据上述信号模型，在高斯白噪声或色噪声背景环境中，估计近场源信号的功率谱强度，得到估计结果如图2所示.

图2中的近场源信号的功率谱强度结果是在实验快拍数为800下的结果，从图可见，在两个谱峰都分别对应横坐标的10 °和30 °两个方位下的功率谱强度估计精度较高，从而分辨出两个方位.以此为基础，在信噪比为30 dB，快拍数为2 000，阵元数为14，做50次Monte-Carlo实验，得到近场源的高阶特征估计结果如图3所示.

从图可见，采用本文模型，能准确估计出近场源的高阶特征参量，提高参数的估计性能，为了对比算法性能，采用本文算法和传统方法，信噪比固定为10 dB，快拍数从200变化到2 000，得到参量估计的均方根误差如图4所示.从图可见，采用本文算法，参量估计的均方根误差较小，能较精确地估计出两个信源的方位角、距离和频率三维参数.

4 结 论

提出一种基于灰色(1,1)模型的近场源高阶特征估计算法.首先构建近场源的参量估计数学模型，给出模型假设条件，采用高阶累积量算法实现对近场源参量的联合估计.研究结果表明，采用本文算法进行近场源的高阶特征参量预计，以较精确的估计出两个信源的方位角，距离和频率三维参数，在雷达、声纳、通信等信号与信息处理中展示了较好的应用价值.

[1] 焦义文,王元钦,马宏,等. 群时延失真对天线组阵合成信噪比的影响分析[J].信号处理, 2015, 31(2):145-153.

[2] 李祖雄. 一类具有反馈控制的修正Leslie-Gower模型的周期解[J].应用数学学报,2015, 38(1): 37-52.

[3] 王瑞，马艳. 基于分数阶傅里叶变换的线性调频脉冲信号波达方向估计[J].兵工学报,2014,35(3):421-427.

[4] 王宝进， 吴淑跃，薛娟. SDD-1改进算法在Hive中应用[J]. 湘潭大学自然科学学报,2014,36(4):77-82.

[5] 房嘉奇, 冯大政, 李进.稳健收敛的时差频差定位技术[J].电子与信息学报, 2015,7(4): 798-803.

[6] 谭家杰，邹常青. 室内多环 LED 的信道特性分析[J]. 系统仿真学报,2013,25(12):2 906-2 911.

[7] 李艳婷，张红伟，师星辰,等. 离散多音调制可见光信道非线性失真及参数优化[J].光电子.激光,2014,25(1):82-88.

[8] 杨波，王志洁. 基于PTRM与DS技术通信均衡性能研究[J].科技通报,2014,30(2):212-214.

[9] 严海芳, 蒋卉,张文权. 用MCEM加速算法估计多序列无根树最优分支长度[J]. 湘潭大学自然科学学报,2014,36(2):13-16.

责任编辑：龙顺潮

Estimation of Near-Field Sources of High Order Characteristic Based on Grey (1,1) Model

LIRui-zhai1*，LIYi-hua2

(1.School of Arts and Science , Sias International University , Xinzheng 451100;2.School of Computer and Information Engineering, Henan University, Kaifeng 475000 China)

The estimation of near-field sources of high order parameters is an important content of the array signal processing. Based on the parameter estimation of high order characteristics of near field source can be achieved on the direction of arrival (DOA) estimation of the frequency, time delay estimation, the estimation of moving target Doppler. Near field source characteristics of the traditional estimation algorithm using single frequency characteristic estimation method cannot achieve the joint estimation of signal parameters. Based on the grey (1,1) near field source with high order characteristic model estimation algorithm，the paper constructed mathematical model for estimating the parameters of near field sources, the spatial spectrum estimation method, to get the spatial information of the orthogonality of the signal subspace and the noise subspace, by changing the grey (1,1) mathematical model to reduce the sensitivity of the characteristic parameters of high order imbalance, combined with characteristics of high order parametric estimation. The simulation results show that the algorithm for the estimation of near-field sources of high order parameters, can be more accurate estimates of two source azimuth, distance and frequency of three-dimensional parameters in radar and sonar, communication, signal and information processing.

near field source; parameter estimation; grey (1,1) model

2015-01-11

河南省重点科技攻关项目(142102210499)

李瑞斋(1980— )，女,河南 南乐人，讲师.E-mail:643292716@qq.com

TN911.2

A

1000-5900(2015)03-00101-06