考虑磁钢磁化方式的永磁电机空载气隙磁场性能分析
李界华, 胡 佳, 文泽军*
(1. 湖南城建职业技术学院,湖南 湘潭 411101;2. 湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201)
考虑磁钢磁化方式的永磁电机空载气隙磁场性能分析
李界华1, 胡 佳2, 文泽军2*
(1. 湖南城建职业技术学院,湖南 湘潭 411101;2. 湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201)
针对磁钢磁化方式影响永磁电机空载气隙磁场性能的问题,建立了永磁电机空载气隙磁场的解析模型.通过对磁钢的两种充磁方式的分析,即径向充磁和两段式Halbach充磁,获得了永磁电机空载气隙磁密径向分量和切向分量的计算方法.选用一台1极12槽永磁有刷直流电机作为对象,利用解析模型计算了空载气隙磁密,通过与有限元仿真结果对比,验证了解析计算结果的正确性.在此基础上,计算了两种充磁方式下的空载气隙磁场径向磁密畸变率,结果显示:永磁有刷直流电机采用两段式Halbach充磁的畸变率明显低于径向充磁.同时,分析了极弧系数、磁钢厚度、极对数、槽口宽与径向磁密畸变率之间的关系,为永磁电机的初始设计提供了参考依据.
磁化方式;解析模型;两段式Halbach充磁;空载气隙磁场;径向磁密畸变率
永磁电机因其结构简单、高可靠性及高效率等优势在各个行业得到越来越广泛的应用.其磁钢的充磁方式伴随着永磁材料的发展以及充磁技术的进步而日新月异.磁钢采用不同充磁方式对电机气隙磁场分布有着比较明显的影响[1,2].气隙磁场的分布是影响电机性能的关键因素之一,对永磁电机不同磁钢磁化方式下气隙磁场性能的研究,将有助于合理选择磁钢磁化方式,充分发挥永磁材料的潜能.
分析永磁电机气隙磁场通常采用有限元法和解析法.有限元法可以仿真较为复杂的电机模型,精度较高,但耗时较长.而解析法虽然需对电机模型进行理想化处理,但解析式能够反映各设计参数与气隙磁密的关系,可直观地调整参数,进行优化.王兴华[3]建立了永磁无刷直流电机径向充磁下空载气隙磁场的解析模型,利用许-克变换构造了能够反映齿槽效应的气隙相对比磁导函数,其计算结果与有限元结果对比,气隙磁密径向分量波形和大小吻合很好.丁晔[4]研究了永磁无刷电机空载气隙磁场半解析法,将解析法与差分法结合,用解析法计算气隙磁场,差分法计算槽域的磁场.沈建新[5]研究了永磁无刷电机平行充磁下气隙磁场的解析计算,并通过有限元计算验证了解析计算的可靠性.范坚坚[6]建立了磁极间隔开的Halbach型磁钢永磁同步电机空载气隙磁场解析模型,详细分析了磁钢厚度、单片磁钢角度与充磁夹角对气隙磁密的影响.刘光伟[7]研究了外永磁转子爪极电机的空载气隙磁场的解析计算方法,给出了该电机二维分析模型下的边界条件,推导了空载气隙磁场的径向和切向磁密的计算方法.Liu[8]在直角坐标系下建立了面贴式永磁无刷电机空载气隙磁场的解析模型,计算了磁极转换区域槽开口区域的瞬时磁场.Dubas[9]采用矢量磁位建立了多极表面式永磁电机的空载气隙磁场解析模型,该模型考虑了径向和平行充磁两种方式,并通过有限元结果与解析结果对比验证了结果的正确性.
在上述研究的基础上,本文建立了两种充磁方式下的空载气隙磁场解析模型,即径向充磁和两段式Halbach充磁.选用了一台永磁有刷直流电机,计算了两种充磁方式下的空载气隙磁密和径向磁密畸变率,并通过有限元法验证解析结果的准确性 .在此基础上,分析了畸变率随结构设计参数的变化规律,为电机的初始设计提供了依据.
1 不同充磁模式下气隙磁密的解析计算
1.1 开路场计算
在极坐标系中,剩磁强度矢量M可表示为
M=Mrr+Mθθ.
(1)
对于磁钢不同的磁化方式,Mr和Mθ可以表达成傅里叶级数的形式,即
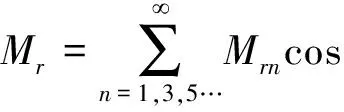
(2)

(3)
式中,Mrn和Mθn表示径向和切向的第n次谐波分量.本文将列出了两种不同充磁方式(即径向充磁、两段式Halbach充磁[1])的电磁场解析表达式,如图1所示为磁钢的两种磁化方式示意图.
图1(a)中的径向充磁只有径向分量,沿每一极弧为一常数.其径向充磁的径向和切向分量的傅里叶级数可表示为

(4a)
Mθn=0.
(4b)
图1(b)表示的是两段式Halbach充磁示意图,其磁块均由平行磁化的磁钢拼合而成,其径向和切向分量的傅里叶级数可表示为

(5a)

(5b)
式中,

(6a)
(6b)

求解泊松方程和拉普拉斯方程和已知的边界条件式[4],可获得不同区域内各向磁通密度分布.气隙磁通密度的径向与切向分量分别为

(7a)

(7b)
当np≠1时,为了方便数值计算,对内/外转子拓扑结构电机进行分开讨论.
内转子结构永磁电机(Rs>Rm>Rr):

(8a)

(8b)

(8c)
外转子结构永磁电机(Rs (9a) (9b) (9c) 当np=1时,则有 (10a) (10b) (10c) 式(8a)、(9a)、(10a)中,A3n由磁钢的充磁方式来决定,具体如下: 当np≠1时,系数A3n可表示为 当np=1时,系数A3n可表示为 1.2 气隙磁导函数计算 为了计算永磁电机的齿槽转矩,必须考虑电机开槽的影响,因此,一般引入气隙相对磁导对开路气隙磁场进行修正.将有限深梯形槽用一无限深的径向开口槽代替,保持无限深开口槽的槽口宽度等于实际槽口宽度,如图2所示,为一个槽口处磁场分布.图3为S域下径向无限槽深模型,序号1~6代表槽周围的点,θ1为槽下沿角度,θ2为槽上沿角度,θs为槽距角,图4为转化后的无齿槽模型. 通过4组保角变换,把永磁电机有齿槽转化成无齿槽分析,并获得复数磁导函数,变换公式表示如下: (11) g′=ln(Rs/Rr). 通过四组保角变换,获得气隙磁密Bs和复数气隙磁导函数λ为 Bs=Bkλ*, (12a) (12b) 式中,Bk=Br+jBθ为K域下气隙磁密,λa为复数气隙磁导的实部,λb为复数气隙磁导的虚部,通过傅里叶级数分解,可得 (13a) (13b) 式中,Qs为永磁电机槽数,λan和λbn为傅里叶系数. 1.3 有槽永磁电机气隙磁密计算 综合式(7a)、(7b)和(12a),有槽永磁电机气隙磁密可表示为: Bsr=Re(Bkλ*)=Brλa+Bθλb, (14a) Bsθ=Im(Bkλ*)=Bθλa-Brλb, (14b) 式中,Bsr、Bsθ分别为气隙磁密径向分量和切向分量. 以上解析计算过程可利用Matlab语言编为程序,从而获得解析计算的结果,同时,通过与Ansoft软件仿真结果对比分析,验证解析结果的正确性.本文选用了一台1极12槽永磁有刷直流电机[10](以下简称PMDCM),对比分析了两种磁钢充磁方式下的空载气隙磁密分布(PMDCM的原始充磁方式为径向充磁).表1为PMDCM的各参数值. 表1 PMDCM各参数列表 由前面的解析算法可容易获得PMDCM的复数气隙磁导函数的实部和虚部,并进一步计算空载气隙磁密分布.图5为气隙磁导函数径向分量和切向分量,图6为解析法得到的PMDCM空载气隙磁密径向分量和切向分量的分布(气隙半径r=Rr+(Rm-Rr)/2处). 由图6和图7可知,与PMDCM初始方案的径向充磁相比,两段式Halbach充磁的气隙磁密径向分量拥有更好的正弦性波形,而切向分量的分布两者差别不大. 为了验证空载气隙磁密解析算法的正确性,将解析法得到的结果与有限元仿真进行对比,其结果如图8所示. 由图8可知,径向充磁和两段式Halbach充磁的解析结果与有限元仿真结果接近、趋势相同,表明了解析计算的有效性. 为了分析PMDCM开槽对气隙磁密的影响,定义径向气隙磁密畸变率为: (15) 式中,Br1和Brn分别为径向气隙磁密基波幅值和n次谐波幅值.由前面解析模型可比较方便地得到PMDCM的空载气隙磁场径向磁密畸变率,计算结果如表2所示. 表2 两种充磁方式下的基波幅值与畸变率 由表2可知,虽然两段式Halbach充磁的空载气隙磁场径向磁密基波幅值小于径向充磁,但是空载气隙磁场径向磁密的畸变率较小,具有较好的气隙磁密分布. 为了得到空载气隙磁场径向磁密畸变率与各参数之间的关系,分别分析了径向磁密畸变率随极弧系数、磁钢厚度、极对数、槽口宽之间的变化规律,其结果如图9所示,其中图9(a)为径向充磁的结构参数与畸变率关系,图9(b)为两段式Halbach充磁的结构参数与畸变率关系. 由图9(a)可知:径向充磁方式下,PMDCM各结构参数与径向磁密畸变率均存在不同程度的变化关系,其中极弧系数在0.45~0.9的范围内径向磁密畸变率先递减后递增,其余各参数与径向磁密畸变率只有单纯的递减或递增关系.同时,极弧系数与极对数对径向磁密畸变率的影响较大,而其他结构参数对径向磁密畸变率的影响较小. 由图9(b)可知:两段式Halbach组合充磁方式下,PMDCM各结构参数与径向磁密畸变率的关系与径向充磁不同.其中系数kR在0.4~0.9之间变化时,畸变率变化比较显著,当kR为5.2左右时,畸变率接近于零.极对数对畸变率的影响也比较大,当极对数大于3以后,畸变率趋于恒定.而磁钢厚度对畸变率的影响与径向充磁相反,槽口开角对畸变率的影响与径向充磁相近. 建立了两种充磁方式下的永磁电机空载气隙磁场的解析计算方法,选择了一台永磁有刷直流电机作为对象,并通过与有限元仿真结果进行对比,得到如下结论: (1) 对比分析了在解析法与有限元法下的空载气隙磁密分布,两者结果趋于一致,证明了解析计算的有效性.在此基础上,计算了两种充磁方式下的空载气隙磁场径向气隙磁密畸变率,结果表明:两段式Halbach充磁的畸变率明显低于径向充磁. (2) 分析了两种充磁方式下空载气隙磁场径向磁密畸变率随极弧系数、磁钢厚度、极对数、槽口宽的变化规律,为电机的初始设计提供了依据. [1] RAHIDEH A,KORAKIANITIS T. Analytical open-circuit magnetic field distribution of slotless brushless permanent-magnet machines with rotor eccentricity[J]. IEEE Transactions on Industry Applications, 2011, 47(12): 4 791-4 808. [2] 李延升, 窦满峰, 骆光照. 不同充磁方式的对转永磁电机气隙磁场性能研究[J]. 四川大学学报(工程科学版), 2014, 46(1): 140-146. [3] 王兴华, 励庆孚, 王曙鸿. 永磁无刷直流电机空载气隙磁场和绕组反电势的解析计算[J]. 中国电机工程学报, 2003, 23(3): 126-130. [4] 丁晔, 章跃进. 表面磁钢永磁无刷电机空载气隙磁场半解析法研究[J]. 电机与控制应用, 2006, 23(3): 7-10. [5] 沈建新, 陈利根. 永磁无刷电机中平行充磁2极气隙磁场的解析计算[J]. 电机与控制应用, 2006, 33(1): 7-10. [6] 范坚坚, 吴建华. 极间隔断 Halbach 型磁钢的永磁同步电机气隙磁场解析计算及参数分析[J]. 电工技术学报, 2010, 25(12): 40-47. [7] 刘光伟, 张凤阁, 魏瀚阳. 外永磁转子爪极电机空载气隙磁场解析计算[J]. 电工技术学报, 2014, 29(1): 52-59. [8] LIU Z J, LI J T. Analytical solution of air-gap field in permanent magnetmotorstaking into account the effect of pole transition over slots[J]. IEEE Transactions on Magnetics,2007, 43(10): 3 872-3 883. [9] DUBAS F, ESPANET C. Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect: no-load vector potential and flux density calculation[J]. IEEE Transactions on Magnetics, 2009, 45(5): 2 097-2 109. [10] 何鹄环. 永磁有刷直流电动机电磁振动与噪声的分析 [D]. 上海:上海交通大学, 2012. 责任编辑:罗 联 Analysis of PM Motor No-Load Air-Gap Magnetic Field Considering Magnet Steel Magnetization Manners LIJie-hua1,HUJia2,WENZe-jun2* (1. Hunan Urban Construction College, Xiangtan 411101;2. Hunan Provincial Key Lab of Health Maintenance for Mechanical Equipment,Hunan University of Science and Technology, Xiangtan 411201 China) Based on the effects of magnetization of permanent magnet (PM) on the no-load air-gap magnetic field distribution, a PM motor analytical model of no-load air-gap magnetic field distribution was built. The method of radial and tangential flux density of no-load air-gap magnetic field were obtained by comparative analysis of two different magnetization manners, namely, radial magnetization and two-segment Halbach magnetization. A one-pole twelve-slot permanent magnetic DC motor was regarded as the object, and no-load air-gap magnetic field density was computed by using the analytical model. Compared with the results of FEA, the effectiveness of analytical model was confirmed. For this, the radial flux density distortion rate of no-load air-gap magnetic field under two different magnetization manners were calculated, and the results reveal that the radial flux density distortion rate of two-segment Halbach magnetization has an obvious low value than radial magnetization. The relations were analyzed between pole embrace ratio, magnet thickness, pole pairs, slot opening and radial flux density distortion rate, which provide bases for original design of PM motor. magnetization manners; analytical model; two-segment Halbach magnetization; no-load air-gap magnetic field; radial flux density distortion rate 2015-04-02 湖南省教育厅科学研究项目 (11C0237) 文泽军(1966— ),男,湖南 湘乡人,教授.E-mail:zjwen732@163.com TM351 A 1000-5900(2015)03-0035-08








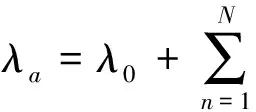

2 空载气隙磁密的有限元验证




3 空载气隙磁密性能分析



4 结 论

