信控道路交叉口过街行人流影响下的右转车辆延误模型研究
李 硕, 李 玲, 李 昂
(湖南大学 土木工程学院,湖南 长沙 410082)
信控道路交叉口过街行人流影响下的右转车辆延误模型研究
李 硕*, 李 玲, 李 昂
(湖南大学 土木工程学院,湖南 长沙 410082)
交通延误是评价城市信控道路交叉口服务水平和车辆通行效率的一个重要指标.未设置右转专用相位的信号交叉口右转车辆与行人的冲突会引起右转车辆的延误.本文从微观角度分析了在未设置右转专用相位的信号道路交叉口右转车辆穿越过街行人流的过程,考虑了右转车辆抢行状况及过街行人不同过街状态,建立并验证了未设置右转专用相位信控道路交叉口右转车辆穿越过街行人流的车均交通延误模型.
交通控制;右转车辆;交通延误模型;车辆抢行
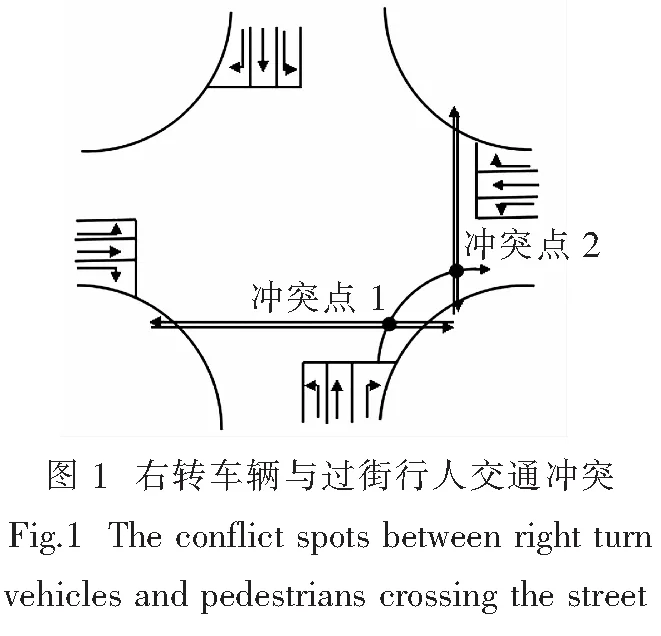
由于右转车辆与其他方向车辆间的冲突微弱,信号道路交叉口不设置右转信号相位可以避免因设置而造成的不必要的交通延误.然而步行是中国城市交通中一种重要的出行方式,在信号道路交叉口进口道右转车辆穿越过街行人流时二者会发生交通冲突,冲突情形如图1所示,这种冲突必然会造成右转车辆的交通延误.在信控道路交叉口,过街行人由于受到过街信号的控制,图1中所示的两处冲突点只有一处发生右转车辆与过街行人的冲突.
交通延误是评价道路交叉口服务水平和车辆通行效率的一个重要指标,国内外学者对交叉口车辆的延误研究很多[1~5].但由于国外信控道路交叉口的过街行人数量相对较少,国外学者开展的关于信控道路交叉口无右转车辆信号控制条件下的右转车辆穿越过街行人流的研究相对较少,且提出的方法和标准并不符合我国的道路交通实际状况.例如Qureshi[6]等用车辆累积排队的多边形法得出了信控道路交叉口右转车辆的平均交通延误,但没有讨论车辆受过街行人干扰所产生的交通延误;Mohammed[7]分析了人行横道处影响行人行为的因素.国内对信控道路交叉口右转车辆穿越过街行人流的研究较多,张茂民[8]等提出了信控道路交叉口右转车辆由于过街行人干扰所产生的交通延误计算方法,但并没有考虑过街行人在接受信号控制条件下的消散情况,也没有考虑右转车辆抢行的状况;杨晓光[9]等推导了穿越过街行人流的右转车辆通行能力模型.
虽然我国道路交通管理条例规定,道路交叉口右转车辆必须让行过街行人,但现场交通调查结果显示,右转车辆在与过街行人发生交通冲突时抢行现象非常普遍.本文结合以上研究成果,对信控道路交叉口右转车辆穿越过街行人流的机理和右转车辆抢行状况进行分析,推导考虑右转车辆与行人发生抢行状况下发生的信控道路交叉口右转车辆延误模型.
1 右转车辆穿越过街行人流过程
城市信控道路交叉口在无右转车辆信号控制条件下的行人过街过程可以分为两部分:(1) 行人过街信号为绿灯(下文简称行人绿灯):这里定义tg为绿灯时长(s),此时过街行人拥有优先通行权,右转车辆需让行行人.然而由于右转车辆不文明驾驶,此过程可能会出现右转车辆抢行行为;(2) 行人过街信号为红灯(下文简称行人红灯):这里定义变量tr为红灯时长(s),此过程由于无行人通过,右转车辆到达时即可自由离去.根据上述分析,信控道路交叉口右转车辆穿越过街行人流的过程可以抽象为:若右转车辆在行人绿灯时到达,选择与过街行人抢行或等待可穿越间隙穿越过街行人流,若一直等不到可穿越间隙则在行人绿灯结束时离开;若右转车辆在行人红灯时到达,即刻自由离去.
由此可以得出,信控道路交叉口在无右转车辆信号控制条件下的右转车辆延误的大小与右转车辆的到达分布、行人过街状态、车辆最小可穿越间隙、右转车辆抢行概率等4个参数相关.
2 交通延误模型建立
因为不同的信控道路交叉口行人的过街状态并不相同,所以右转车辆交通延误的产生过程和机理也不同.本文主要研究信控道路交叉口无右转车辆信号控制条件下的右转车辆有抢行发生的情况下的交通延误.有道路交通调查表明信控道路交叉口右转车辆加减速延误在6~10 s之间[10],本文取其平均值t0=8.8 s.
2.1 行人过街服从泊松分布右转车辆延误模型
假设信控道路交叉口无右转车辆信号控制条件下的右转车辆到达与过街行人冲突区域(以下简称冲突点),需要选择等待可穿越间隔穿越或选择立即抢行.若选择等待,当第1个过街行人可穿越间隔出现时右转车辆离开,此时该车产生交通延误.
信控道路交叉口无右转车辆信号控制条件下的右转车辆在行人绿灯状态到达时,若不选择抢行,其交通延误过程及机理详见图2.本文定义以下变量:信控道路交叉口右转车辆到冲突点的时刻用随机变量x表示.为方便计算,设行人绿灯结束的时刻为时间的零点,则x的大小等于行人绿灯结束的时刻与右转车辆到达时刻的差值.x的概率密度函数为g(x),对应的概率分布函数为G(x).随机变量T为信控道路交叉口右转车辆的交通延误时间(s),右转车辆在行人随机过街状态时到达的条件下0≤T≤tg,T的概率密度为f(T),对应的概率分布为F(T).

信控道路交叉口过街行人服从泊松分布,可得到此时信控道路交叉口无右转车辆信号控制条件下的右转车辆延误的概率分布为指数分布[11],所以
F(T)=p{T≤t}=1-e-λ1t,
(1)
式中:λ1为信控道路交叉口过街行人流的可穿越间隔的强度(辆/s);t为时间(s),t≥0.
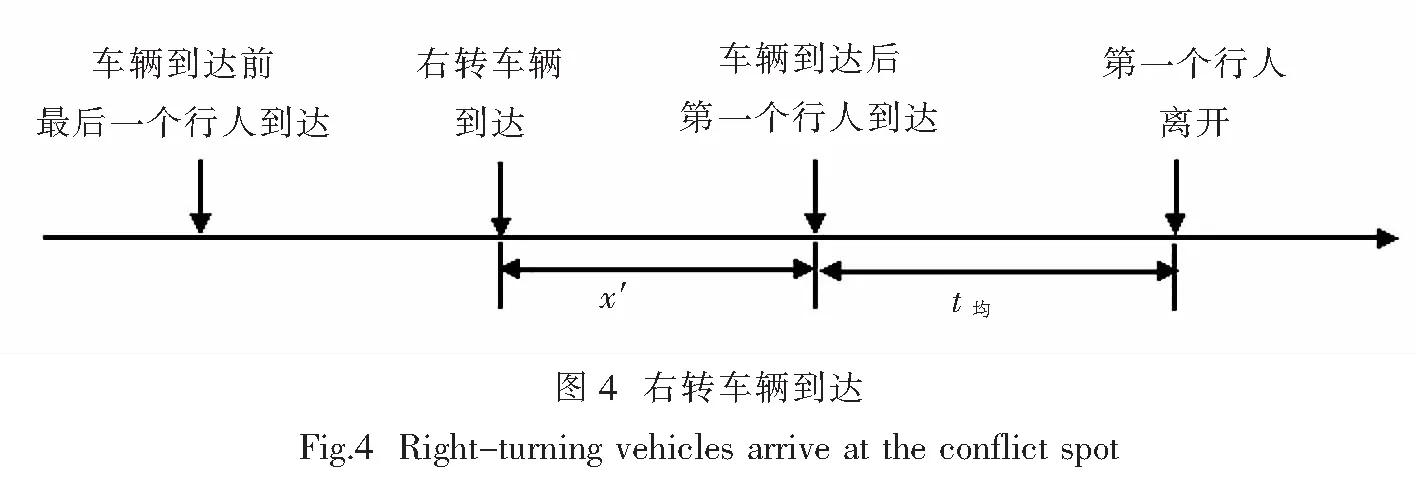
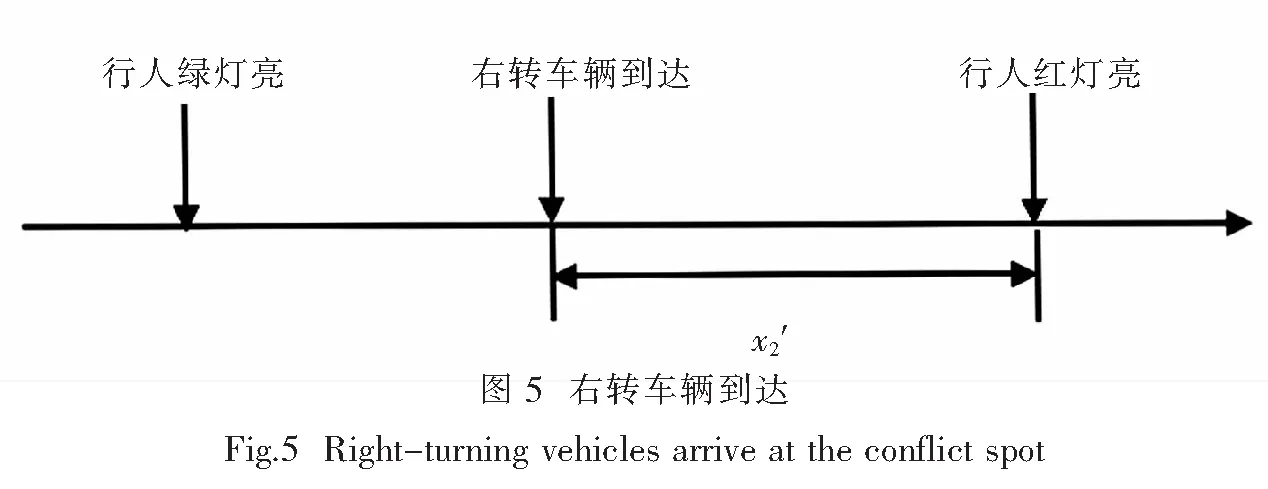
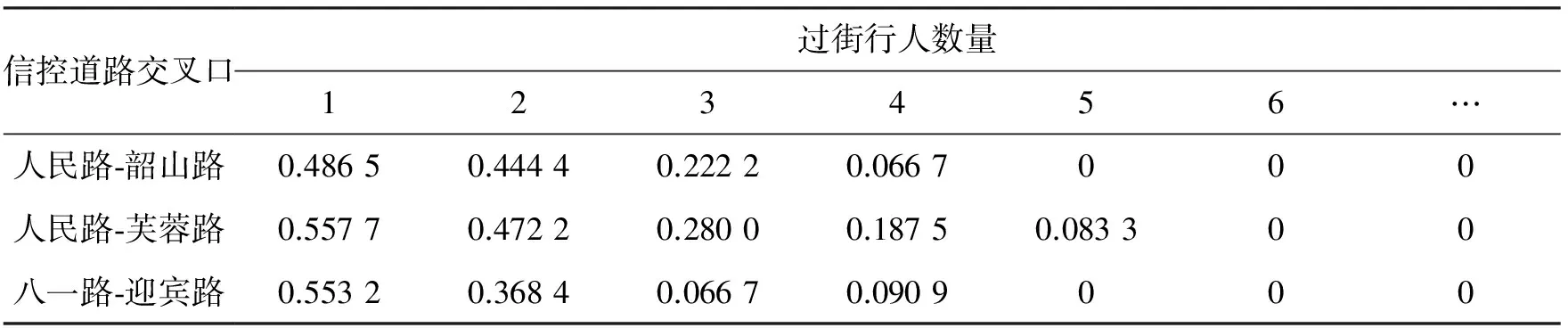
右转车辆到达信控道路交叉口这一事件本身也具有随机性,在右转车辆于x时刻到达的条件下,其交通延误概率分布函数为F(T,x),对应的概率密度为f(T,x).当0≤T 由于行人在随机过街状态中服从泊松分布,所以相邻过街行人群之间的时距h(s)大于最小可穿越间隙a的概率为 P{h>a}=e-qa, (2) 式中:q为信控道路交叉口过街行人流量(人/h);a为信控道路交叉口相邻两群过街行人之间最小可穿越间隔(s). 那么根据负指数分布的概率密度可得出信控道路交叉口过街行人流的可穿越强度λ1为 λ1=qe-qa/3 600/3 600. (3) 本文假设信控道路交叉口右转车辆到达冲突点的时刻服从泊松分布,则x服从负指数分布,其概率密度为 g(x)=λ2e-λ2x, (4) 式中:λ2为信控道路交叉口单位时间间隔右转车辆平均到达率(辆/s). 信控道路交叉口行人随机过街的时间区间为[0,tg],在此区间内右转车辆的交通延误为 D1=t0+∬tf(t,x)g(x)dtdx, (5) 式中:f(t,x)为信控道路交叉口右转车辆随机交通延误的概率密度. 信控道路交叉口相邻两群过街行人之间最小可穿越间隔乘以过街行人步速,则为信控道路交叉口相邻两群过街行人之间最小可穿越距离.设定最小可穿越范围为以右转车辆行车中线为中心线,以人行横道为方向,以最小可穿越距离为长度.当信控道路交叉口无右转车辆信号控制条件下的右转车辆到达冲突点时,车辆是否选择抢行与最小可穿越范围内过街行人数量高度相关.通过对长沙人民路-芙蓉路交叉口、人民路-韶山路交叉口、八一路-迎宾路交叉口交通观测数据,得出右转车辆抢行概率随最小可穿越范围内过街行人数量变化明显,其关系如图3所示. 由图3可得出右转车辆的抢行概率基本呈线性关系,可分别建立一元线性回归模型为 人民路-韶山路:y1=-0.112 0x1+0.595 4,R12=0.915 2; 人民路-芙蓉路:y2=-0.115 6x2+0.668 2,R22=0.983 2; 八一路-迎宾路:y3=-0.109 9x3+0.564 6,R32=0.812 0. 根据实际道路交通观察和数据统计结果可得出如下结论:右转车辆抢行概率虽在不同信控道路交叉口略微有所不同,但右转车辆的抢行概率均与最小可穿越范围内的行人数量呈线性关系.因此可认定,某个右转车辆的抢行与否与最小可穿越范围内的行人数量高度有关.令y1、y2、y3分别取0,得到的x1、x2、x3均小于6,因此可认定当最小可穿越范围内的行人数量大于6时,右转车辆不会选择抢行.由于到达车辆距行人的安全距离为3 m[12],行人间距小于3/v人时,右转车辆出于安全考虑,尽管最小可穿越范围内行人数量小于6,右转车辆也不会抢行.由此可得信控道路交叉口无右转车辆信号控制条件下的右转车辆平均抢行概率是由信控道路交叉口右转车辆与过街行人最小可穿越范围内有i名过街行人时右转车辆的抢行概率、最小可穿越范围内过街行人数量及右转车辆选择抢行的最小间距三个关键参数所决定. 行人间距大于3/v人的概率为 (6) 式中:λ3为信控道路交叉口单位时间间隔内过街行人平均到达率(人/s);v人为信控道路交叉口过街行人平均过街速度(m/s). 当右转车辆到达时,冲突点处有一名行人的概率为p1,此时右转车辆抢行的概率为P1;同理,冲突点处有i名行人的概率为pi,右转车辆在此时抢行的概率为Pi,由于过街行人随机到达,可将冲突点处行人个数的概率视为离散型随机变量,根据概率论[13]中数学期望(均值)的定义可得信控道路交叉口无右转车辆信号控制条件下的右转车辆平均抢行概率为 (7) 式中:P为信控道路交叉口无右转车辆信号控制条件下的右转车辆平均抢行概率;Pi为信控道路交叉口无右转车辆信号控制条件下的右转车辆与过街行人最小可穿越范围内有i名过街行人时右转车辆的抢行概率;pi为最小可穿越范围内有i名过街行人的概率(过街行人的到达服从泊松分布,计数间隔等于信控道路交叉口最小可穿越距离/过街行人步速). 若是信控道路交叉口右转车辆选择抢行,认为抢行后的交通延误为0.因此,综合来看,右转车辆在行人绿灯时间段到达的交通延误为 Dtg泊=D1(1-P). (8) 通过信控道路交叉口右转车辆平均延误为 (9) 式中:Q为信控道路交叉口右转车辆交通量(辆/h);Qg为行人绿灯通过信控道路交叉口右转车辆交通量(辆/h). (10) 将式(1)、(6)、(7)代入到式(8)得 (11) 2.2 行人过街服从均匀分布右转车辆延误模型 过街行人到达信控道路交叉口服从均匀分布,此时过街行人时距为h=3 600/q(假设右转车辆熟悉路况,已知过街行人流量).根据过街行人时距的大小,可将信控道路交叉口无右转车辆信号控制条件下的右转车辆穿越行人流分为三种情况:(1) 过街行人时距大于最小可插车间隙,此时即使右转车辆到达时冲突点处有行人,右转车辆让行延误也不会很大,因此右转车辆在此状况下选择让行.过街行人从进入冲突点到离开冲突点所需时间为t均=信控道路交叉口右转车道宽度/过街行人步速;(2) 过街行人间的距离小于车辆与行人间安全距离3 m,即过街行人间距小于3/v人,右转车辆由于交通安全问题无法抢行,只能等待行人绿灯结束后离开;(3) 过街行人间距小于最小可插车间距但大于3/v人,此时右转车辆没有耐心等待而选择抢行. (1) 过街行人时距大于最小可插车间隙 定义以下变量:信控道路交叉口无右转车辆信号控制条件下的右转车辆到达冲突点的时刻用随机变量x1′表示.为方便计算,设车辆到达后第一个行人到达时刻为时间零点,则x1′的大小等于右转车辆到达时刻与车辆到达后第一个行人到达时刻的差值.x1′的概率密度函数为g1′(x1′),对应的概率分布函数为G1′(x1′).随机变量T1′为信控道路交叉口右转车辆的交通延误时间(s),且0≤T1′ (12) 右转车辆交通延误的分布函数为 (13) 右转车辆到达服从泊松分布,g(x1′)=g(x).所以过街行人时距大于最小可插车间隙的右转车辆平均延误为 (14) 将式(5)代入式(16)得 (15) (2) 过街行人间距小于3/v人 过街行人间距过小,右转车辆无法通行,只能等待行人绿灯结束.定义以下变量:信控道路交叉口右转车辆到冲突点的时刻用随机变量x2′表示.为方便计算,设行人绿灯结束时刻为时间零点,则x2′的大小等于右转车辆到达时刻与行人绿灯时刻的差值.x2′的概率密度函数为g2′(x2′),对应的概率分布函数为G2′(x2′).随机变量T2′为信控道路交叉口右转车辆的交通延误时间(s),且0≤T2′ 右转车辆到达服从泊松分布,g2′(x2′)=g(x),右转车辆由于安全考虑,到达后一直等待行人绿灯结束,即x2′=T2′,根据泊松分布的平均值可得 D均2=E(x2'), (16) 即 (17) (3) 过街行人间距小于最小可插车间距但大于3/v人 右转车辆在此种状况下抢行容易,所以视为右转车辆到达即抢行,故没有延误,即 D均3=0. (18) 综合以上结论,行人过街服从均匀分布情况下右转车辆的延误为 (19) 即 (20) 以长沙市人民路-韶山路、人民路-芙蓉路及八一路-迎宾路信控交叉口为例.人民路-韶山路交叉口和人民路-芙蓉路交叉口在人民路上有人行横道,而韶山路及芙蓉路上没有人行横道(但是有过街地下通道),八一路-迎宾路交叉口两条道路上都有人行横道.三个信控道路交叉口行人到达均为泊松分布. 经过交通调查所获得的信控道路交叉口右转车辆抢行概率与过街行人数量如表1所示. 表1 信控道路交叉口右转车辆抢行概率与过街行人数量之间的关系 经过道路交通调查所获得的当行人处于随机过街状态时信控道路交叉口右转车辆与过街行人发生冲突地点处的过街行人数量概率如表2所示. 表2 信控道路交叉口最小可穿越范围内过街行人数量概率 信号道路交叉口右转车辆交通延误模型计算结果见表3. 表3 模型计算结果 在信控道路交叉口人行横道处,右转车辆穿越过街行人流时会受到过街行人的影响,从而产生交通延误.本文从微观交通的角度出发,在考虑右转车辆抢行的状况下,建立了信控道路交叉口右转车辆与过街行人发生冲突时右转车辆的交通延误模型,并以长沙市人民路-韶山路、人民路-芙蓉路及八一路-迎宾路信控交叉口为例进行了延误计算.对此领域的进一步研究有一定的参考意义. [1] 陈河明,李硕,高岩,等.信号交叉口期望交通延误模型及计算方法研究[J].交通运输系统工程与信息,2013,13(3):170-178. [2] 李硕,高岩,张建龙,等.基于VISSIM仿真的内侧左转车流延误分析[J].交通运输系统工程与信息,2012,12(4):50-56. [3] RICHARD E A.Delay at a fixed time traffic signal:theoretical analysis[J].Transportation Science,1972,6(3):260-285. [4] 李硕,王春梅,李昂. 基于公交优先的道路交叉口可变相位多层模糊控制[J].湘潭大学自然科学学报,2013,35(1):67-73. [5] 李硕,张谞博,周慧,等. 城市信号控制交叉口延误计算与仿真研究[J].湘潭大学自然科学学报,2011,33(4):45-50. [6] QURESHI M A,HANLD.Delay model for right-turn lanes at signalized intersections with uniform arrivals and right turns on red[J].Transportation Research Record,2001,1 776:143-150. [7] HAMED M M. Analysis of pedestrians’ behavior at pedestrian crossings[J]. Safety Science, 2001, 38(1): 63-82. [8] 张茂民,刘伊生,裴玉龙.基于行人的信号交叉口右转车控制条件[J].公路交通科技,2008,25(9):136-139. [9] 杨晓光,马万经,林瑜.两相位信号控制交叉口行人专用相位设置条件研究[J].公路交通科技,2005,22(1):127-131. [10] 邵长桥.城市道路信号交叉口通行能力研究[M].北京: 人民交通出版社,2013: 23-25. [11] 王炜,过秀成.交通工程学[M].南京:东南大学出版社,2005:89-107. [12] 中华人民共和国道路交通安全法[Z]. [13] 概率论与数理统计教程[M].北京:高等教育出版社, 2008. 责任编辑:罗 联 Research on Delay Model of Right-Turning Vehicles on Signalized Intersections under the Influence of Crossing Pedestrians LIShuo*,LILing,LIAng (College of Civil Engineering, Hunan University, Changsha 410082 China) The traffic delay is an important index to evaluate the service levels and the operation efficiency at a signalized intersection.The conflict between right turning vehicles and pedestrians at the signalized intersection where being no exclusive right-turn traffic phase will lead to traffic delay .This paper analyzed the process of the right-turning vehicles traversing pedestrians crossing at a signalized intersection where there is no right turn signal from microscopic perspective, considering the right-turning vehicles which traverse the pedestrian crossing area forcibly and the difference of states of pedestrians crossing at a signalized intersection, set up and verify an average traffic delay of right-turning vehicles traversing pedestrians crossing area at a signalized intersection where there is no right turn signal. traffic control; right-turning vehicle; traffic delay model; forcible vehicle 2015-03-31 李硕(1958— ),男,湖南 长沙人,博士,教授.E-mail:dabertlee@hnu.edu.cn U491 A 1000-5900(2015)03-0027-08
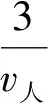

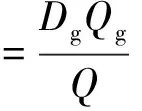


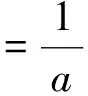
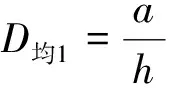
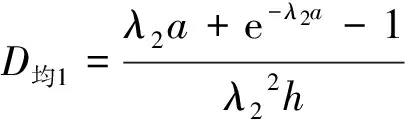
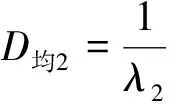
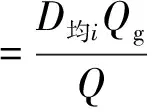
3 实例验证


4 结 语

