蝴蝶定理初等证明的开放性教学

【摘 要】蝴蝶定理是数学史上一道经典的几何题，几百年来对它的研究一直不断更新和发展。本文结合蝴蝶定理在我国的研究历史，研究蝴蝶定理初等证明的开放性，为将蝴蝶定理带进课堂提出教学建议。

【关键词】蝴蝶定理；开放性教学

1蝴蝶定理简介

1.1 蝴蝶定理的一般形式简述

如图一所示，EF是⊙O的弦，P是EF的中点，AB、CD是两条过点P的弦，连接AD、BC，分别交弦EF于点M、N，则P是M、N的中点。

1.2 我国蝴蝶定理的研究历史

蝴蝶定理是近代初等几何中的名题之一，同时也是欧氏平面几何的一个有趣的论断。早在1815年，它作为一个征求证明的问题，刊载于西欧的一本杂志《Gentlemans Diary（男士日记）》上，引起了数学爱好者们的关注[1]。但是“蝴蝶定理”这个叫法最早出现在1944年出版的《American Mathematical Monthly（美国数学月刊）》上，因其几何形状与蝴蝶相似而命名[2]。200年来，我国数学爱好者们不断给出新的、简洁的证明方法，给这个“老问题”注入了“新活力”。

我国对蝴蝶定理的研究，开始于20世纪80年代。1985年，杜锡录教授①在《平面几何中的名题及其妙解》一文中，将蝴蝶定理普及给大众[3]。同年，杨路教授②在《谈谈蝴蝶定理》一文中指出，将弦EF的中点P推广到弦EF的任意一点，可得蝴蝶定理的坎迪（A.L.Candy）蝴蝶形式[4]：

………………………（1）

其中，EP=a，FP=b，MP=x，NP=y。

不久之后，马明学者③在《蝴蝶定理的变异》一文中，将弦EF上的点P，拓展到弦EF外，开拓了蝴蝶定理研究的新方向[5]。这一时期主要讨论圆（椭圆）中蝴蝶定理的各种变形，直至1990年，中国数学竞赛选拔题中出现了筝形蝴蝶定理：

如图二所示，筝形ABCD中，AB=AD、BC=CD，过对角线交点O作直线EF、MN，连接EN、MF，分别交BD于点P、Q，则PO=Q。

1990年，筝形蝴蝶定理出现在全国高中数学冬令营选拔赛题目中。此后，我国对蝴蝶定理的研究进入了一个新的高潮，不断拓展对定理的变形和推广。

1992年，张景中院士④在《蝴蝶定理的新故事》一文中，反复运用线段比与面积比的互相转化，证明了蝴蝶定理，并进行推广[6]。同年，李长明教授对筝形蝴蝶定理进行了证明与推广[7]。1993年，陈举、邓御寇、刘海蔚从射影几何的角度证明蝴蝶定理，并编写进《高等几何》教材中[8]。1998年，赵临龙从射影几何的角度，分析蝴蝶定理的推广命题，并给出二次曲线的蝴蝶定理结论[9]，此结论已被《中国数学文摘》及《美国数学评论》摘录，成果斐然。2001年，王绍恒、王昌成在《用射影几何观点导出的欧式几何命题》一文中，同样从射影几何的角度给出了蝴蝶定理的证明[10]。

2001年，全国初中数学竞赛中，出现了蝴蝶定理变形题。2003年，椭圆内的蝴蝶定理变形题出现在北京市数学高考试题中，引起了国内数学爱好者的关注。对蝴蝶定理的研究推广至今也没有结束，这道经典几何题的开放性使它很适合进入到高中课堂。

2 蝴蝶飞进課堂—蝴蝶定理在高中课堂中的应用

2.1 蝴蝶定理的开放性

随着蝴蝶定理研究的深入，蝴蝶定理的证明不仅有许多高观点下的证法，更有许多适合高中生的、初等数学的证法。这些证法的条件和结论都可以使开放的，能够拓展到其他情形。蝴蝶定理的初等证明可以从多方位、多角度、多层次让学生探索，具有一定的挑战性、层次性和开放性，并且具有相当大的可以发展的空间，并有效的拓展了学生的学习空间。

我国新课程标准也倡导就同一问题提出不同层次的开放性问题，使不同的学生得到不同的发展，来培养学生的创造性思维和探索创新能力。在教学过程中穿插一些开放性题，打破了每道题都有其对应的标准答案的传统观念，打破思维定势，使学生的思维更加灵活多变。

随着多媒体技术在课堂上的应用和发展，蝴蝶定理的图像演示可以利用动画等多媒体手段予以展示。这不仅契合了蝴蝶定理的变化性，使学生体会到数形结合的思想， 而且形象直观生动，激发学生的创新思维。利用多媒体技术，学生可以进行动态作图，动态计算证明，发现新现象，探索新问题。

2.2 蝴蝶定理的教学建议

蝴蝶定理的推广证明可以作为一个探究性学习活动来进行。

在问题的呈现环节，教师应充分利用多媒体资源的优势，动态的设置和展示蝴蝶定理的开放性条件和结论，引起学生探究兴趣，激发内在学习动机，使学生主动的参与到问题解决的过程中来。

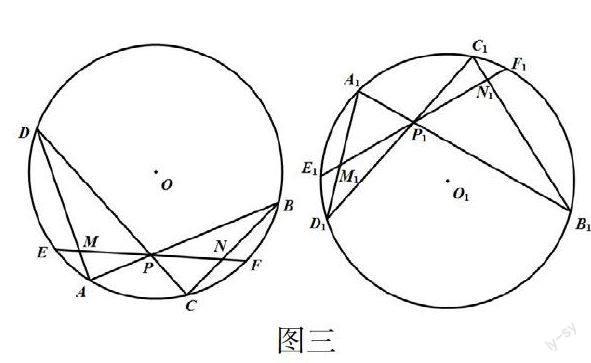
在蝴蝶定理的教学环节，教师应为学生创设生动的情景，通过动态图形的变换，构造不同条件、不同位置下的蝴蝶定理（如图三），促使学生突破思维定势，灵活的思考。进而给出条件：EF是⊙O的弦，P是EF的中点，AB、CD是两条过点P的弦，连接AD、BC，分别交弦EF于点M、N。然后让学生关于图中的线段、面积的数量关系进行讨论和猜测。鉴于动态展示的优势，学生容易得出一些合情推理，但是推理还需严谨的论证，学生便会主动的参与到论证结论的环节中去。

在蝴蝶定理的探究结论环节，学生要利用之前观察动态图形变换得出的合情推理，进行猜测性判断，并利用测量工具对未知量进行测量，得出初步结论，如：△DPA∽△BPC、MP=PN、EM=NF等。对于为证明的结论，必定会有质疑的声音。因此，教师与学生共同动手操作，改变弦和点的位置，观察并度量面积、线段长度的变化，得出新结论：△DPA∽△BPC，MP=PN。

学生通过多媒体改变参数，得出了初步结论，但是由于多媒体技术的局限性，还不能直接给出证明。教师与学生共同讨论，灵活思考，从不同的角度找到证明结论的方法。

探究结束后，教师可根据探究活动的效果，对学生再次启发引导，给出一个新的条件，如：蝴蝶定理只能在圆中成立么？还能在什么图形中成立呢？通过不断的实验和探索，利用已学过的点、线、圆锥曲线等构造新的几何图形，来将蝴蝶定理不断延伸拓展，共同讨论，得出一系列变形，使蝴蝶定理在更多图形中翩翩飞舞。这样连续的设问保证了教学活动的连续性和有效性，为学生营造了动手实验、合作交流、共同完成的学习氛围。

注释：

①杜锡录[1941-1994]，山东济南人，中国数学会普及委员会副主任，山东大学数学系副教授。

②杨路[1936-]，广州大学数学与人工智能国际交流中心主任，研究员，博士生导师，第十届全国人大代表。

③马明[1927-2013]，江苏省南京人，南京师范大学附属中学特级教师，数学教育学者。

④张景中[1936-]河南省汝南县人，中国科学院院士，计算机科学家，华中师范大学国家数字化学习工程技术研究中心学术委员会主任。

参考文献：

[1]方禾.蝴蝶定理[J].科技创新导报，2011（21）：255-256.

[2]周建伟.Steiner定理与蝴蝶定理[J].数学通报，2000（12）：22-23.

[3]杜锡录.平面几何中的名题及其妙解[J].数学教师，1985（1）：16-20.

[4]杨路.谈谈蝴蝶定理[J].数学教师，1985（2）：19-21.

[5]马明.蝴蝶定理的变异[J].数学教师，1985（6）：1-3.

[6]井中.蝴蝶定理的新故事[J].中学数学，1992（1）：1-4.

[7]李長明.筝形性质的推广与蝴蝶定理的关联[J].数学通报.1993（2）.

[8]刘海蔚，陈举，邓御寇.高等几何[M].重庆：西南师范大学出版社，1993.

[9]赵临龙.射影观点下的蝴蝶定理[J].湖南教育学院学报，1998（2）.

[10]王绍恒，王昌成.用射影几何观点导出的欧式几何命题[J].南京师范大学学报：自然科学版，2001（1）.

作者简介：

王梦瑗（1991.10～），女，汉族，山东淄博人，宁夏师范学院数学与计算机科学学院教育硕士专业学位（学科教学·数学）在读研究生。