中职数学过程教学的策略探微

岑一杰

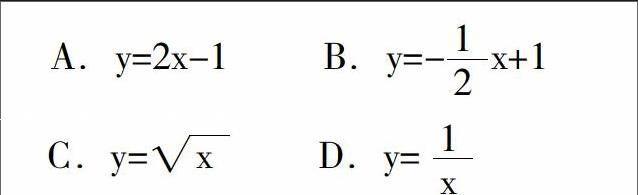
摘要：数学教学的过程是认识数学概念，运用数学定义，体会数学方法和思想的过程。数学教学的目标是提高学生的数学素养和数学品质，而良好的数学素养和品质是在分析问题和解决问题的过程逐步形成的。本文通过概念教学的“回归”，引入教学的“感悟”以及例题教学的“体验”，串起中职数学过程教学的实践与思考。

关键词：中职数学；过程教学；体验

“使职高学生形成一定的数学素养和数学品质”是中职数学教学的核心任务。我们认识到，数学教学的终极目标就是提高学生的数学素养和数学品质，而良好的数学素养和品质是在分析问题和解决问题的过程逐步形成的，是潜移默化的东西，是稳定的，是能够伴随人一生并帮助人走进技术领域的内在动力和媒介。通过数学学习，使学生对数学与现实世界的联系、数学的探索过程、数学的文化价值以及数学知识的特征有所认识和体会；使学生在兴趣与动机、自信与意志、态度与习惯等方面有所发展；使学生在定量思维、空间观念、合情推理和演绎等方面有所发展；使学生在提出问题、分析问题、解决问题以及交流的反思方面获得发展。因此，教学过程中学生的思维体验、认知过程中的感悟、以及从教学素材中得到的结论将是提高学生数学素养和数学品质的助推剂。鉴于此，笔者从概念教学的“回归”、引入教学的“感悟”以及例题教学的“体验”进行了策略探微。

一、概念教学的“回归”——发现与生成

新课的大部分内容都是对概念的教学，概念教学的核心任务是通过创设情境、组织好教学素材，使学生通过情境素材的观察、操作、实践、分析、提炼、归纳，能够发现概念的形成过程，更充分地理解概念，运用概念。为了达到这个目的，必须促使学生能够在运用的过程中不断的体会和领悟，并在体会的基础上使学生解决好所面临的相关问题。因此，数学概念的教学过程不是从讲授定义到运用定义的这样一个单一的过程，而是根据学生现有的认知程度，通过呈现问题、分析问题、解决问题、得出结论，并在结论的基础上引发概念，然后通过学生的感知表述出来（可能是肤浅的），在学生看似“肤浅的结论”的基础上不断运用、修正、总结、完善的过程。如在《函数的单调性》这节课的教学中，有这样一个课例片段：在学生已基本掌握了函数单调性的概念及其（当X1f（X2））推导关系后，学生的思维模式往往容易倾向于一个极端：“就是对定义和概念的理解有所降低，机械地套用公式”。为了解决这个问题，突破学生的模式化思维的局限，课堂教学中特意设计了这样一个问题：

下列函数在定义域上不是单调函数的是（ ）

A.y=2x-1 B.y=-x+1

C.y= D.y=

大部分同学受前面学习经验的影响，毫不犹豫地选择了C答案。这时教师没有给出一个肯定的答复。部分同学开始怀疑刚才答案的正确性了，有的同学感觉D是正确的但是不敢确定。这时教师提问：“什么是函数的单调性，使用推导关系的条件是什么？”，通过师生交流和总结得到三个条件：①定义域内的任意X②当X1f（x2））③单调函数是定义域 I上的增函数（或减函数）。继续提问：“如果C正确，那么问题是否符合以上三个条件呢？”。学生回答：“符合三个条件，因为y=在定义域[0，+∞]上满足三个条件”。教师追问：“根据题目要求，只有答案D是正确的，为什么y=在定义域I上不是单调函数呢？”。学生回答：“取两个特殊值X1=-1，X2=1，则f（-1）f（x2）”，继续追问：“那么函数y=的单调区间是什么呢？”。师生讨论得出：函数y=在区间[-∞，0]上是减函数数，在区间[0，+∞]上是减函数。

评析：在这个课例中，学生不仅加强了推导关系的运用和概念的理解，而且对以前所学的知识得到了巩固和发展。就《函数的单调性》这节课而言，完全可以在课题引入后，直接告诉学生推导关系使用的基本条件。但是这样所形成的思维深度远没有在克服思维定势后显得强烈、深刻。重视对数学概念的教学，循序渐进地去感知概念、运用概念、分析概念、最后透彻概念，克服模式化思维对学生的负面影响。因此，有关数学概念的教学应该是学生在不断分析问题和解决问题的过程中自然形成的，是教师的引导和学生的感悟的再生华过程。正如建构主义学习理论所说：“教学活动是一种特殊的认知建构活动，即在教师的启发和指导下，学生自主地建构知识的活动”。数学教学是让学生在不知不觉中与教师一起参与并体验知识的发生和发展的过程，是立足于学生，着眼于学生，让学生深入课堂、体验课堂、不断适应新问题、形成灵活多变的思维方式的过程。

二、教学引入的“感悟”——延续与创新

新课引入的恰当与否对于一节课的成功实施是至关重要的。良好的教学引入往往具备这样的特点：能够将学生的思维方式自然地过渡到教学内容的主题；能够结合学生的特点，合理地运用数学活动和数学试验，让学生在活动参与的过程中体会新课的主旨；能够体现学生的背景生活，激发学生浓厚的兴趣。

（一）呈现式教学引入

这种教学引入的主要特点是教学素材具有良好的规律性和可观察性，并且与教学主题具有很强的相关性，很容易过渡到教学的主体部分，让学生通过自主发现的方式领会到数学概念和定义，在理解的过程中体现出知识的延续性。如在余弦定理的教学中呈现了这样几个图形问题让学生解决：

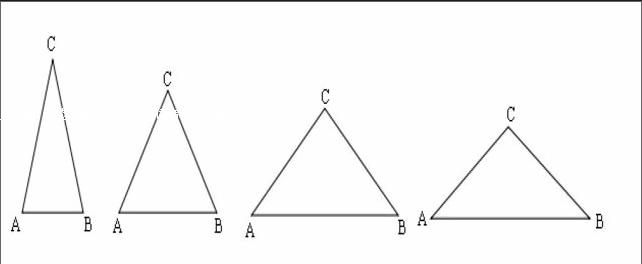
以上四个三角形均为等腰三角形，两腰的长度均为，顶角的度数分别为30°、60°，90°、120°，试求顶角C所对边AB的长.

师：从第一个三角形到第四个三角形，其顶角所对AB边的长是怎样变化的？AB的长度最大的是哪个三角形，怎样计算出的？

生：AB长度随着顶角的增大而增大，其中第四个三角形的AB最大为，通过作底边AB的高，利用直角三角形性质求出。

编辑 ∕高 伟