对一道中考题的赏析、探究及反思

☉广东省广州市花都区炭步镇炭步初级中学 汤妙娟

对一道中考题的赏析、探究及反思

☉广东省广州市花都区炭步镇炭步初级中学 汤妙娟

一、题目鉴赏分析

题目（2014年山东淄博·23）如图1，四边形ABCD中，AC⊥BD交BD于点E，点F、M分别是AB、BC的中点，BN平分∠ABE交AM于点N，AB= AC=BD.连接MF，NF.

（1）判断△BMN的形状，并证明你的结论；

（2）判断△MFN与△BDC之间的关系，并说明理由.

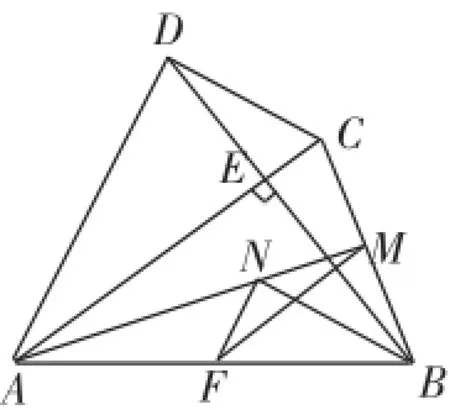
图1

1.题目分析

题目设置本着“面向全体、兼顾选拔、力求创新”的基本原则，遵循“注重基础，稳中求变”的基本思路，既突出了对数学主干知识的考查，又加强了对双基知识的考查力度，同时还注重了题目的综合性.题目设计中考查了中学数学的多个主干知识，包括相似三角形的判定与性质，等腰直角三角形，三角形中位线定理，等腰三角形三线合一，是一道几何综合题，难度不是很大，题目放在试卷中倒数第二题的位置，得分率偏低.学生感觉困惑在哪里？让我们赶紧走近这一道中考题，来体会题目内在的“魅力”.

2.图形分解

教材是中考命题的主要素材，纵观近几年的中考题，每年都有大量的题目直接出自教材，或在教材的基础上，改造整编，繁衍生息.本题也不例外，细细分析，可以把这一题目中的图形分解为三个出自教材的基本图形，分别是：等腰三角形的“三线合一”；三角形的内角平分线相交于一点；三角形的高相交于一点.三个基本图形链接精巧，环环相扣，浑然一体，尽显命题者匠心独运的风格，当然，这一切都源于思考的魅力.

基本图形1：等腰三角形的“三线合一”（如图2）.

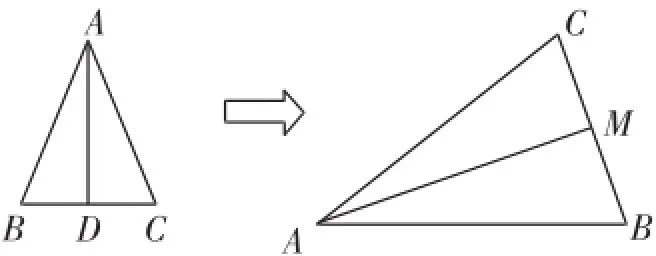
图2

人教版义务教育课程标准实验教科书八年级上册第13章《轴对称》第三节主要研究等腰三角形，是初中数学的主干知识，本题将这一基本的图形横放，部分考生就不知道AM⊥BC了（如图2），说明灵活运用所学知识的能力有待加强，也说明命题人善于从学生身边的题目取材，善于从图形变换中考查学生的图形迁移能力.

基本图形2：三角形的内角平分线相交于一点（如图3）.

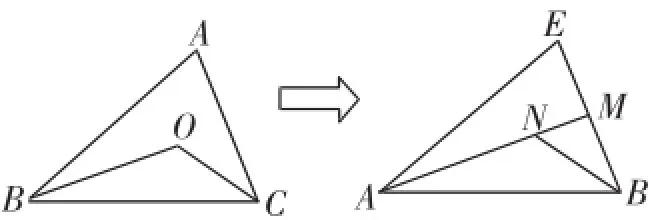
图3

基本图形3：三角形的高相交于一点（如图4）.

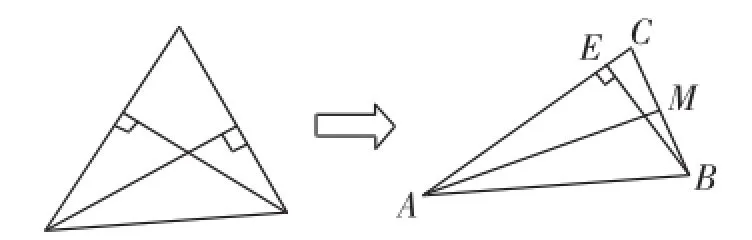
图4

三角形的高相交于一点这一基本图形也是日常练习题中经常见到的，由图4我们就可以得到很多相等的角和相似三角形，所以我们很容易得到∠CAM=∠CBE.在图1中，根据FM∥AC，我们就可以得出∠CAM=∠FMN，进而得到∠FMN=∠CBD，这是确定△MFN与△BDC相似的关键.

基于三个基本图形的构建，就可以轻松地瓦解这一道“难”题了.看来我们可以把“复杂”的中考题分解为熟悉的简单图形，而如何深挖教材，提炼我们熟悉的基本图形，并对图形进行深入探究是几何复习的关键环节.

二、题目拓展探究

1.提炼基本图形，感知模型

通过对这一道中考题目图形的分解探究，结合教材的内容，在复习三角形相似时，除了平时学生们很熟悉的“A型”“X型”“斜截型”“蝴蝶型”“双高型”“三高型”“反射型”外，笔者还引导、帮助学生提炼了如图5所示的基本图形，为学生更好地运用基础知识，感知基本模型创造了条件.

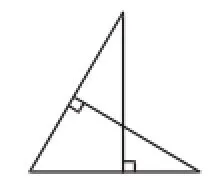
图5

通过提炼变式基本图形，为学生运用基础知识，感知基本的数学模型，营造了和谐的氛围.这样让学生能够轻松地接受这一基本图形，为下面的图形变式探究，打下了坚实的基础.

2.探究基本图形，深化认识

基本图形给出后，若直接抛出问题，让学生去探究，学生的思维将在教师的牵引下行进，主动探究的热情将大打折扣，对于基本图形的认识也会停留在表面上.基于这样的思考，笔者试图让学生根据基本图形或变换图形，自己设计问题，来加深对基本图形的认识.在展示课上，笔者真正感受到：只要敢于放手，学生就会给课堂带来活力，就会展示自己的精彩.现把学生提出问题与解决问题的过程整理如下.

问题1：如图6，图中相似三角形有几对？

除个别基础比较弱的学生找不全外，大部分学生能够轻松找出6对相似三角形，相似三角形的判定及相似的基本图形“斜截型”与“蝴蝶型”的知识，得到了巩固和提升.

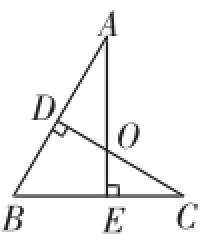
图6

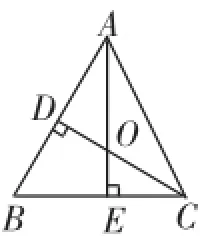
图7

问题2：连接AC，如图7，图中相似三角形又有几对？

问题给出后，学生们努力寻找新的相似三角形，结果发现并没有增加新的相似三角形，尽管走了一些“弯路”，但是加深了学生对基本图形的理解，也为进一步的探究做好了铺垫.

问题3：若再连接DE（如图8），△BDE与△BCA相似吗？为什么？

问题4：如图8，△DOE与△AOC相似吗？为什么？

问题5：如图8，图中相似三角形有几对？

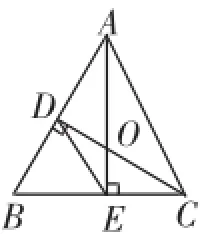
图8

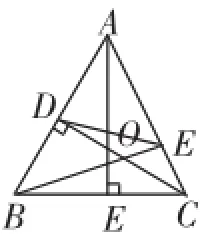
图9

对于问题3，由△CBD∽△ABE（这是问题1中的一对相似三角形）得到又因为∠B=∠B，所以△BDE∽△BCA.通过两次相似，最终利用两边成比例且夹角相等得出了结论.

对问题4的求解更是精彩.

思路1：在探究问题3的基础上，学生明白了为了证△DOE∽△AOC，可以先证△AOD∽△COE，得到.又因为∠AOC=∠DOE，所以△AOC∽△DOE.

思路2：由问题3可知△BDE∽△BCA，所以∠BDE=∠ACE，而∠EDO=90°-∠BDE，∠CAO=90°-∠ACE，所以∠EDO=∠CAO.又因为∠DOE=∠AOC，所以△DOE∽△AOC.通过两角相等证出两三角形相似，这是对问题4的探究的一个亮点.

问题3与问题4掀起了探究基本图形的高潮，对于问题3的探究，部分同学自认为DE∥AC，让问题探究走入了“迷途”，通过小组合作交流才找到问题解决的途径.在问题3的基础上探究问题4，学生的思路更加开阔，通过后面的拓展探究，学生还可以根据圆的知识来解决问题4.将图8旋转变式得到图9，通过上面的问题，让学生再进一步深化认识基本图形.

笔者让学生根据图形来设计问题，对学生来说是一个挑战，更是一次锻炼升华的机会，学生一听说自己来设计题目，兴趣大增，个个跃跃欲试，当然，提出问题比解决问题更困难，但是这种角色的转变，大大提升了学生的参与度和学习热情，更为关键的是结合图形的变式，让学生经历了从问题的提出到问题的解决整个过程，深入思考探究了这个基本图形的本质，达到了在思考中运用、在运用中提升的目的.较好地实现了数学教学中知识与方法、过程与结果的和谐统一，真正起到了润物无声的效果.

3.拓展基本图形，活学活用

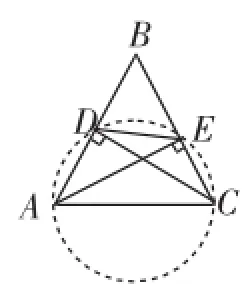
图10

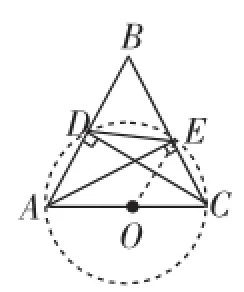
图11

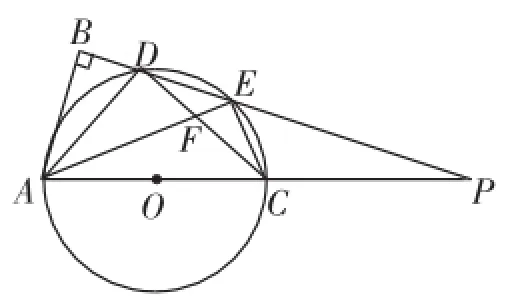
图12

如果将图9与圆结合，就是一道几何综合题了，因此，笔者适时地将圆引入基本图形中，让学生在知识的交汇处继续拓展探究.

问题6：过A、D、C三点作圆，圆心在哪里？点E在这个圆上吗？（让学生感知A、D、C、E四点在同一个圆上，因而得到图10）

问题7：通过问题6的探究，你对问题4还有什么新的办法？

增加条件“AE平分∠BAC”，学生们还设计了下面的问题.

问题8：如图10，△ABC是什么三角形？（再次回扣中考题的基本图形“等腰三角形‘三线合一’”）

问题9：试说明DE=CE.

问题10：证明BD·BA=BE·BC.

问题11：若连接OE（如图11），试说明OE与AB的关系.

问题12：如图11，△OEC与△BDE相似吗？为什么？

由图11，若只截取A、C、E、D的部分，延长DE与AC相交于一点P，作AB⊥BP，如图12，这就是2014年泸州市中考数学第24题的图形.

在图12中，若AE平分∠BAC，DE=2，PC=AC，又可以设置很多问题，如下所示.

问题13：证明△PCE∽△PDA.

问题14：证明△ABD∽△ADF.

问题15：求PE的长.

问题16：求⊙O的半径r.

问题17：求BD的长.

通过拓展探究，再一次提高了学生的模型识别能力与知识的迁移能力，提升了思维的深度.从复杂的图形中分离出“基本图形”，在问题解决中综合运用所学的知识，如相似三角形的判定与性质，勾股定理，圆的基本知识等，使学生在图形变化过程中感悟“万变不离其宗”的道理，让学生在一系列的变化过程中识别基本图形，从而找到问题的根本解决办法，达到“解一题、通一类”的教学目的.

三、反思

1.教得活是学得活的前提

在日常的教学中，如果单从一个具体的图形去分析，就提论题，充其量是解决了一个问题，题目的内在价值将囿于一域，如果立足于题目的基础之上，提炼出内蕴的基本图形，再通过变式，加强对基本图形的灵活运用，切实地让学生展开探究活动，图形的内在价值才能够释放出来.

教材中的习题都是经过专家精心打磨的精品，在几何复习中，如何挖掘题目内在的能量，引导学生从题目中提炼“基本图形”是关键.在教学设计时，不能轻易地让教育资源流失，要善于通过一系列的图形变式和一系列的问题串，去开启学生的思维之门.

2.方法为先，思维为本

问题是思维的源泉，美国著名的数学家哈尔莫斯说过，有了问题，思维才有了方向；有了问题，思维才有了动力；有了问题，思维才有了创新.利用基本图形的变式，让学生提出问题，是把“以教为本”的教学转化为“以学为本”的教学的一个有效策略.学生不是一个等待填满的容器，而是急需点燃的火把.没有学生的积极参与，再好的教学设计也会黯然失色.因此，通过问题的层层推进，将学生的思维激活，让数学知识不再枯燥，让课堂不再沉闷，永远是一线数学教师追求的目标.笔者认为能否为学生搭建一个探究的平台，为学生长远发展提供原动力，是衡量教学成败的关键之一.在几何教学中，要逐步引导学生从复杂的图形中分离出基本图形，进而实现将复杂的图形简单化，最终实现把不会的问题转化为会的问题.当然，仅从复杂的图形中分离出基本的图形是不够的，还要引导学生会在综合性的问题中，构造熟悉的基本图形，教会学生方法，让学生受益终生.

3.培养学生的几何直观能力十分重要

《全日制义务教育数学课程标准（2011版）》将几何直观列为十大核心概念之一.笔者认为，在日常教学中注重引导学生从具体的图形中提炼基本图形是培养学生几何直观能力的重要途径.在具体题目中，应充分利用基本图形的性质分析、解决问题，借助基本图形帮助学生直观地理解数学问题，进而为学生几何推理论证奠定基础.如在复习解直角三角形这一章时，若在教学中，一会儿让学生计算河的宽度，一会儿是旗杆的高度，又是金字塔的高度，课堂上学生明白的问题，但课后练习时若换了题目的“另一张脸”，学生又摸不着头了，因此及时帮助学生提炼基本图形十分重要.

图13

构建了基本图形后，遇到实际问题时，让学生自己判断该用哪个基本图形，对于每个基本图形，该怎样分析，然后通过图形的变式，将实际生活中的仰角、俯角、方位角融入问题设计中，锻炼学生从实际问题中识破基本图形的能力，才能真正达到“做一题、会一类”的目的，才能让学生脱离题海，最终实现为学生减负.

四、结束语

多年的教学经历，让笔者越来越感受到探究数学教学的“奥妙”是一段没有终点的旅程，是一本只有逗号、没有句号的“经卷”，不管怎样，笔者会坚持不懈地走下去，持之以恒地向教育前辈学习、向杂志学习、向身边的榜样学习，相信功夫不负有心人.Z