液体晃荡荷载与液舱运动相位关系的数值研究

赵小西，卫志军，阮诗伦，岳前进，陈晓东（大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

液体晃荡荷载与液舱运动相位关系的数值研究

赵小西，卫志军，阮诗伦，岳前进，陈晓东
（大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

该文从相位角度出发，采用CFD的数值方法研究简谐激励下液体晃荡整体荷载与液舱运动的相位关系。首先，通过模型实验验证数值方法的可靠性，然后，以横荡激励下的二维矩形舱晃荡为例，研究不同载液率工况下，相位差和晃荡整体荷载幅值随激励频率的变化关系。结果表明：基于VOF法的数值模拟能较好地模拟液舱内液体晃荡；在自由面共振频率附近（0.8 f0～1.2 f0），相位差随激励频率增加而增大；频率比相同时，相位差随载液率的升高而增大；相位差90°时，相位差对应频率低于共振频率，且与晃荡荷载最大值对应频率基本相等。

液体晃荡整体荷载；相位关系；数值模拟；局部冲击荷载；模型实验

0 引 言

带液舱运载装备在环境荷载下的运动激励舱内液体产生晃荡，晃荡引起的冲击荷载作用于舱壁，进而影响工业结构的整体运动姿态。特别在舱内液体部分装载时，剧烈晃荡引起的抨击压力可能造成工业结构的严重失稳，但同时这种剧烈的晃荡也可以加以合理利用，如船舶减摇水舱、调频液体阻尼器（TLD）等的使用。液舱晃荡对结构整体运动产生不同的影响，与舱内液体晃荡整体荷载与结构运动的相互作用关系密切相关。张力等[1]将调频液体阻尼器（TLD）产生的晃荡整体荷载等效成结构附加阻尼，认为当液体振荡频率与结构运动的频率接近或一致时，TLD产生与结构运动相反的液体动压力可以减小主体结构的振动。马维良、焦侬等[2]针对可控式被动减摇水舱，提出最佳相位PD控制策略，使舱内液体的振荡运动和船舶横摇运动大致相差90°相位，满足最佳减摇相位的要求，其减摇效果要优于常规控制。Faltinsen和Timokha[3]在分析自由液面减摇舱时，提出晃荡整体荷载与船体横摇相位差接近90°时，具有较好的减摇效果，并据此通过已知的船体横摇周期推出被动减摇舱的载液深。以上研究出于减振(摇)为目的，主要关注液体晃荡整体荷载与结构运动相位差90°情况，而对于相位差随激励频率变化及载液率变化的规律却缺乏细致深入的研究。针对这一问题，本文研究了简谐运动激励下，舱内液体晃荡整体荷载与液舱运动的相位差变化规律。

1 相位分析原理

考虑舱内液体晃荡影响的主体结构运动，可简化为在受到环境荷载作用的结构上附加流体晃荡整体荷载作用所产生的整体运动，结构运动方程可以表达为：

式中：M、C和K分别为单自由度系统的质量、阻尼和回复力（刚度）系数；Fw（t）为结构外激激励，Fs（t）是运动过程中舱内液体作用于结构的晃荡整体荷载。

结构受到外界简谐激励x（t）=Acos（ω t）时，Faltinsen等[3]将晃荡整体荷载处理为：

其中：φ为晃荡整体荷载滞后于结构运动的相位差，ω为简谐激励的圆频率。

（2）式可以变换为：

将（3）式代入结构运动方程（1）可得：

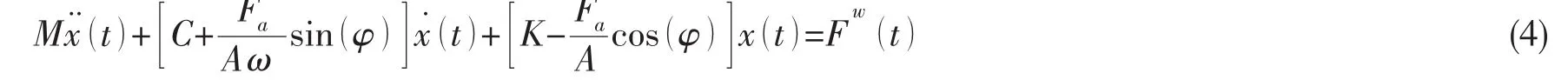
从变形后的运动方程可以看出，可以将晃荡整体荷载的影响，附加到结构运动原来的阻尼和恢复力（刚度）系数上，令：

从（5）式可以看出，液体晃荡附加阻尼Cs和附加恢复力（刚度）系数Ks的大小由液体晃荡整体荷载幅值Fa和相位差φ决定，因此，确定Fa和φ的大小及变化规律是十分必要的。

2 液舱晃荡数值模拟

2.1 VOF方法

与理论解析法相比，采用基于计算流体力学的数值模拟进行液舱晃荡问题研究可以突破理论方法无法模拟波面翻转等物理强非线性现象的限制，能够模拟剧烈的流体晃荡运动；与模型实验相比，采用数值模拟方法更加方便，而且能够对晃荡现象进行综合分析。为了解决液体晃荡中自由液面的变化描述，许多学者采用了不同的方法来捕捉和追踪自由液面，通常采用的有VOF法[4-5]、MAC法[6]和LEVEL-SET法等[7]。其中VOF法的基本原理是通过研究网格单元中流体和网格体积比来确定自由面和追踪流体的变化。VOF法使得流体的质量得到守恒，并可跟踪自由液面上发生翻转、吞并、飞溅等复杂的自由面现象，并可以与各种离散方法结合，因而成为解决这一问题的重要工具[5，8]。

本文基于VOF法，采用流体计算商用软件ANSYS FLUENT进行计算，数值计算设置如表1所示。

表1 数值计算设置Tab.1 Numerical calculation settings

2.2 液舱计算模型

本文采用的二维矩形液舱模型尺寸为L×H×B=970 mm×927 mm×158 mm，网格划分间距为10 mm，共有144 336个网格，如图1所示。

液舱做强迫横荡运动，横向激励为x（t）=Acos（ωt），其中：A=50 mm，ω为激励圆频率。ω表达式[3]为：

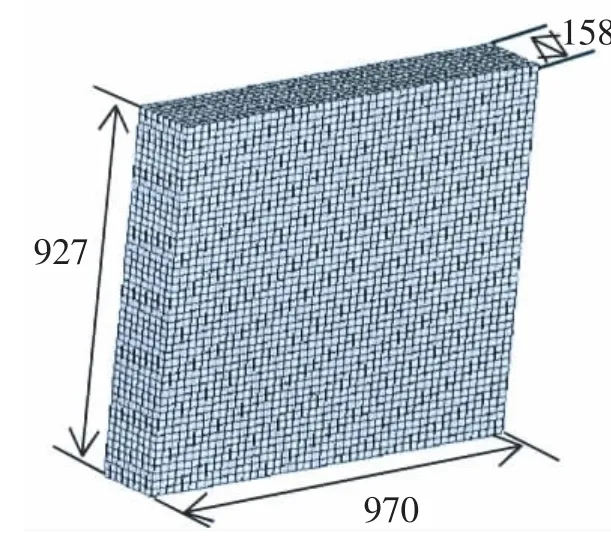
图1 二维矩形液舱模型的网格剖分图（单位：mm）Fig.1 Schematic diagram of 2D rectangular tank model(unit:mm)

3 液体晃荡整体荷载与液舱运动

3.1 数值模拟方法验证

液舱晃荡的准确模拟是研究液体晃荡荷载的前提。据此，通过开展液舱晃荡模型实验，验证数值模拟结果的准确性。基于ANSYS FLUENT平台的液体晃荡整体荷载计算是局部冲击压强的积分，因此，通过验证局部冲击压强同样能反映液舱晃荡整体荷载数值模拟的准确性。

验证选取了20%H和50%H两种载况(即液深分别为185 mm和464 mm)下局部冲击压强的时程进行对比。冲击压强监测点及实验液舱模型如图2、图3所示，监测点的选取参考了卫志军等[10]面向晃荡荷载研究的模型实验，能够反映液体剧烈晃荡时的荷载响应。

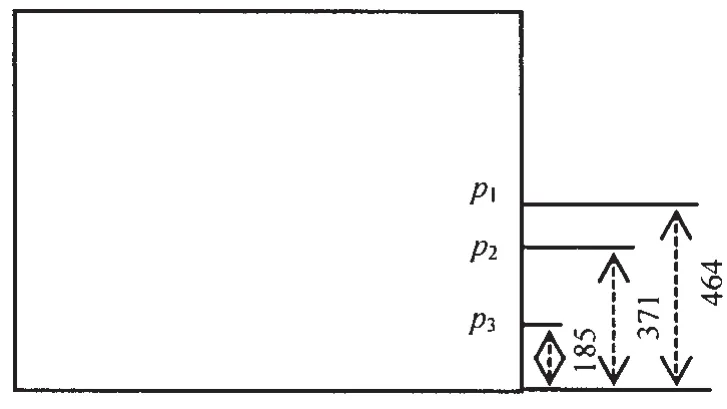
图2 各监测点位置（单位：mm）Fig.2 Locations of monitoring(unit:mm)

图3 实验液舱模型Fig.3 Tank model of experiment

图4为载液50%H，激励频率f/f0为1.0时，p1（自由液面）和p2处冲击压强数值模拟与实验值的对比。从图中可以看出，不同监测点处数值模拟结果与实验值均吻合良好：尽管由于共振导致液体晃荡的非线性使得晃荡局部冲击压强在幅值上与实验结果存在一定误差，但压强时程上的周期性变化趋势却基本同步。

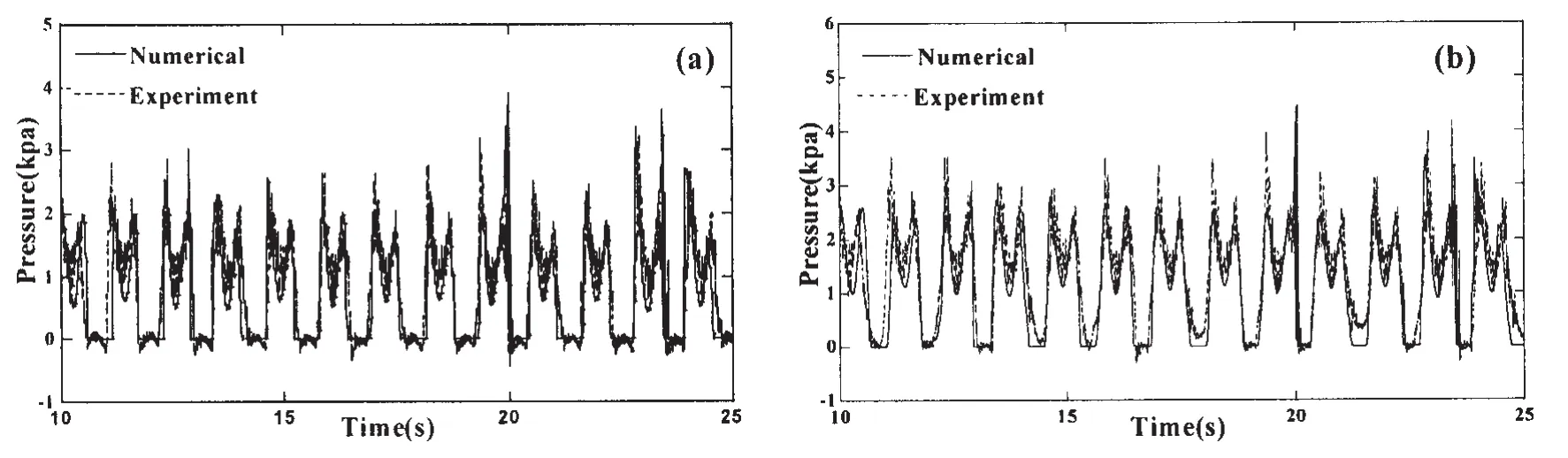
图4 50%H载液，f/f0=1.0时，冲击压强数值与实验结果时程对比：（a）p1；（b）p2Fig.4 50%H filling level,f/f0=1.0,comparison between numerical simulation and experiment on pressure:(a)p1;(b)p2

图5为载液20%H时，激励频率f/f0分别为0.8和1.0时，同一监测点p3（自由液面）处冲击压强数值模拟与实验值的对比。从图中可以看出，非共振与共振情况下数值模拟与实验值均吻合良好，尤其在非共振时，在进入稳态后，无论冲击压强幅值大小还是压强周期性变化趋势均基本一致。

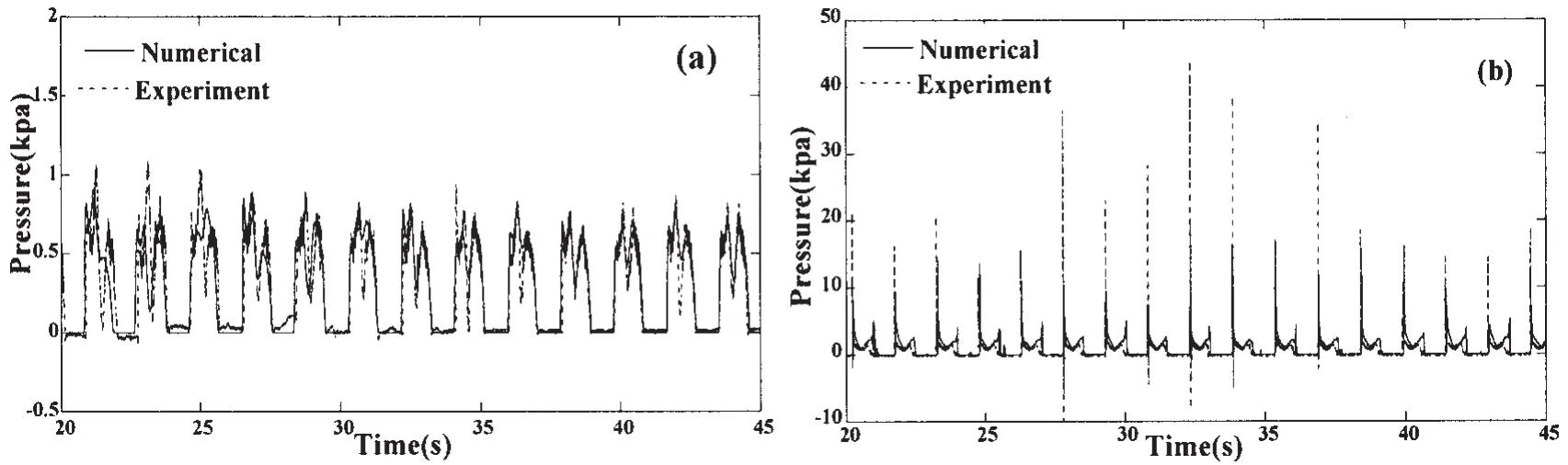
图5 20%H载液，p3处冲击压力数值与实验结果时程对比：（a）f/f0=0.8；（b）f/f0=1.0Fig.5 20%H filling level,comparison between numerical simulation and experiment on pressure with p3:(a)f/f0=0.8;(b)f/f0=1.0

上述对比结果说明，采用VOF法模拟液体晃荡荷载是比较可靠的：尽管在接近共振时，液体晃荡局部冲击压强幅值存在一定误差，但冲击压强周期性变化趋势基本同步，并且在非共振时，数值与实验结果吻合良好。对于本文而言，数值模拟晃荡局部冲击压强带来的幅值误差，是可以忽略的，因为剧烈晃荡时的局部冲击压强峰值是高频荷载，对于晃荡整体荷载而言，其所包含的高频荷载对结构整体运动的影响而言是较小的[11]。因此，在处理基于ANSYS FLUENT监测的晃荡整体荷载时，可以采用恰当的拟合方法获得有效的晃荡整体荷载。

3.2 计算工况选取

基于ANSYS FLUENT模拟的液体晃荡整体荷载，监测的是横向左右舱壁上的液体晃荡整体荷载。根据液体晃荡特点，在不同载液率时，分别呈现不同特性，因此选取了三种具有代表性的载液率工况20%H、30%H和50%H。

当外激激励频率接近第一阶固有频率时，舱内液体发生共振，此时晃荡非常激烈，这种极端工况是工程界研究液体晃荡对整体结构运动影响的重点，因此本文选取的激励频率在0.6 f0～1.3 f0，接近共振频率会进行适当加密。

3.3 晃荡整体荷载计算结果处理

图6为载液20%H，激励频率f/f0为1.0时，即共振时，液舱晃荡整体荷载的变化曲线，其中虚线表示通过数值模拟的结果，可以看出，晃荡整体荷载虽然呈周期性变化趋势，但并不完全规则，为了便于数值表达，利用MATLAB对原始数据进行拟合处理。基于MATLAB的Fourier拟合表达式如下：

其中：a0，an，bn为常数，k表示拟合阶数，k=1，2，3，···，8。分别对液体晃荡整体荷载进行各阶拟合，对比可知：

其中：a（0k）和ω(k)分别代表进行k阶拟合时的a0和ω值，f为液舱运动的激励频率。

由此可见，液体晃荡一阶整体荷载的响应频率与液舱运动频率一致，超过二阶（包括二阶）晃荡整体荷载的响应频率大于液舱运动的频率。考虑高频（相对于结构运动频率）荷载对结构整体运动的影响较小[11]，可以忽略不计，因此，对晃荡整体荷载采用一阶拟合，结合（7）式和（8）式，拟合后的晃荡整体荷载表达式为：

其中：ω为液体晃荡的圆频率。

图6中实线即为采用一阶拟合后液体晃荡整体荷载的变化曲线，拟合后的晃荡整体荷载变化曲线能够很好地反映晃荡整体荷载的变化，且其变化频率与液舱运动的频率相等，为晃荡整体荷载与液舱运动的相位差分析提供了可行性。

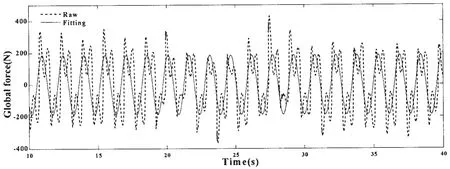
图6 20%H载液，共振时，流体晃荡整体荷载原始和拟合后变化曲线Fig.6 20%H filling level,raw and fitting global force with an resonance frequency

3.4 相位差计算

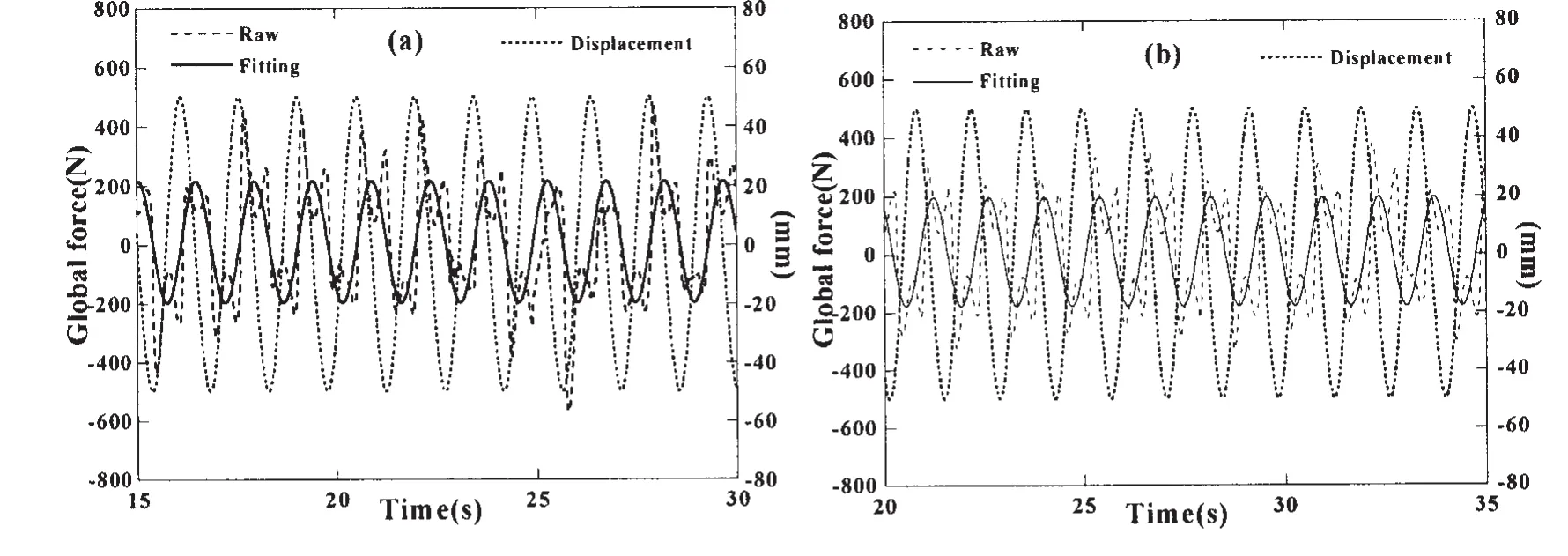
图7为载液30%H，激励频率f/f0分别为0.9、0.95、1.0和1.2时，液体晃荡整体荷载与液舱运动位移的时程对比曲线。从图中可以看出，激励频率不同，晃荡整体荷载与液舱运动在时域内的相对变化也不相同，这种不同可以通过液舱晃荡整体荷载滞后于液舱运动的相位差直观反映。相位差的计算如下：

其中：ΔT为晃荡整体荷载（拟合）滞后于液舱运动的时间之差，f为激励频率。

3.5 计算结果分析

图8为三种不同载液率下，晃荡整体荷载与液舱运动位移相位差随频率变化的曲线。从图中可以看出，相位差均随频率呈递增变化，变化范围为0°～180°，且变化主要发生在共振区间段（0.8 f0～1.2 f0）；在共振区间，同一激励频率比对应的相位差随载液率的升高而增大；相位差90°对应的频率低于共振频率：载液20%H时，发生在频率0.95f0附近；载液30%H，发生在频率0.9f0附近；载液 50%H时，发生在0.85 f0附近。

图9为三种载液率下，晃荡整体荷载大小随频率变化的曲线。从图中可以看出，整体荷载呈单峰变化，峰值对应的频率随载液的不同而不同：20%H载液时，发生在共振频率附近，载液30%H和50%H时，则分别发生在频率0.85 f0和0.9 f0附近。

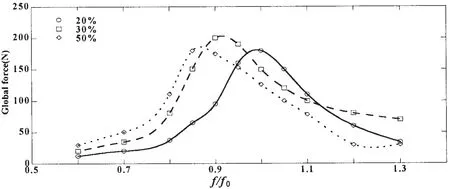
图9 载液不同，流体晃荡整体荷载随频率变化曲线Fig.9 The relationship between sloshing-induced global force and oscillation frequency

综合图8、图9可知，液体晃荡整体荷载与液舱运动相位及整体荷载幅值变化主要发生在共振区间；相位差90°对应频率低于共振频率；且相位差90°对应频率与晃荡整体荷载峰值对应频率：20%H载液率时，前者对应频率低于后者频率约0.05 f0，30%H和50%H载液率时，两者频率相等。

4 结 论

本文采用基于CFD的数值模拟方法，对二维矩形舱横荡激励下的液体晃荡整体荷载与液舱运动的相位差及荷载幅值随外激激励频率的变化关系进行研究。通过对比数值模拟与模型实验所监测的局部冲击荷载值时程，验证了基于VOF法的数值模拟方法的可靠性。然后利用数值模拟方法，对比不同载液率下相位差及晃荡整体荷载的数值模拟结果，获得以下结论：

（1）各载液率下，相位差均随激励频率增加而增大，在共振区间（0.8 f0～1.2 f0）对频率变化敏感，变化范围为0°～180°；

（2）载液不同，同一频率比对应的相位差也不相同，随着载液的升高呈增大趋势；

（3）相位差为90°时，相位差对应频率低于共振频率，并随着载液率的升高，偏离程度呈增大趋势：20%H，30%H和50%H载液时，分别低于共振频率约0.05 f0，0.1 f0和0.15 f0。

（4）相位差90°时，相位差对应频率与晃荡整体荷载最大值对应频率基本相等（20%H载液时，前者低于后者约0.05 f0）。

根据本文研究表明，液舱晃荡整体荷载与结构运动的相位关系及整体荷载大小与结构运动频率及载液率存在对应关系。通过分析相位差和晃荡整体荷载大小随结构运动频率及载液率的变化规律，然后结合结构运动方程，能够用于进一步分析液舱晃荡对结构整体运动姿态影响。而且，通过对液舱晃荡产生的附加阻尼Cs和附加刚度Ks等参数进一步研究，还可以直接为减摇舱及TLD设计提供参考。

[1]张 力.导管架海洋平台冰激振动控制的实验研究[D].大连:大连理工大学,2008. Zhang Li.Experimental study on ice-induced vibration mitigation of jacket offshore platforms[D].Dalin:Dalian University of Technology,2008.

[2]马维良,焦 侬.可控式被动减摇水舱最佳相位PD控制策略研究[J].船舶工程,2012,1(34):36-39. Ma Weiliang,Jiao Nong.Research on optimal phase PD control strategy of passively controlled anti-rolling tank[J].Ship Engineering,2012,1(34):36-39.

[3]Faltinsen O M,Timokha A N.Sloshing[M].Cambridge:Cambridge University Press,2009.

[4]Hirt C W,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39:201-225.

[5]刘桢兵.基于VOF法的液舱晃荡数值模拟及载荷计算[J].重庆理工大学学报（自然科学）,2011,25(3):24-29,61. Liu Zhenbing.Numerical simulation of liquid tank sloshing and pressure calculation based on Volume of Fluid method[J]. Journal of Chong Qing University of Technology(Natural Science),2011,25(3):24-29,61.

[6]Mikells N E,Journee J M J.Experimental and numerical simulations of sloshing behavior in liquid cargo tanks and its effect on ship motions[C]//National Conference on Numerical Methods for Transient and Coupled Problems,July 1984. Venice,Italy,1984:274-278.

[7]Zhu Renqing,Wu Yousheng,Atilla N.Numerical simulation of liquid sloshing-a review[J].Shipbuilding of China,2004,45 (2):14-27.

[8]沈 猛,王 刚,唐文勇.基于改进VOF法的棱形液舱液体晃荡分析[J].中国造船,2009,50(1):1-8.Shen Meng,Wang Gang,Tang Wenyong.Numerical analysis of liquid tank sloshing based on Volume of Fluid method[J]. Shipbuilding of China,2009,50(1):1-8.

[9]Thiagarajan K P,Rakshit D,Repalle N.The air-water sloshing problem:Fundamental analysis and parametric studies on excitation and fill levels[J].Ocean Engineering,2011,38:498-508.

[10]卫志军,岳前进,张文首,等.大尺度储舱内流体晃荡砰击压力的测量方法研究[J].中国科学,2014,44(07):746-758. Wei Zhijun,Yue Qianjin,Zhang Wenshou,et al.Experimental investigation of violent slamming pressure in large-scaled tank[J].SCIENTIA SINICA Phys,Mech&Astron,2014,44(07):746-758.

[11]Huang Z J,Danaczko M A,Esenkov O E,Martin C B,O’Donnell B J,Yung T W.Coupled tank sloshing and LNG carrier motions[C]//The International Society of Offshore and Polar Engineers Conference(ISOPE),June 21-26,2009.Osaka, Japan,2009:92-104.

Numerical study on phase relation between sloshing-induced global force and tank motion

ZHAO Xiao-xi,WEI Zhi-jun,RUAN Shi-lun,YUE Qian-jin,CHEN Xiao-dong
(State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology,Dalian 116024,China)

From phase analysis point of view,this paper presents the phase relation between the sloshing global load and tank motion under harmonic forced excitation based on the CFD method.And the sloshing model tests were carried out to verify the reliability of the numerical method.Then,the phase differences between the sloshing global load and the motion of a 2D-rectangular tank and the amplitudes of sloshing global load with forced-frequencies are obtained for different filling levels.The results show that the tank sloshing can be simulated well by VOF method;the phase differences raise when increasing forced-frequencies around resonant frequencies of free surface(0.8 f0～1.2 f0);the phase differences also increase for higher filling levels at same frequency ratio;the frequency for 90-degree phase difference is less than the resonant frequency and it is roughly equal to that for the maximum sloshing global load.

sloshing global load;phase difference;numerical simulation;pressure;model test

U661.3

A

10.3969/j.issn.1007-7294.2015.08.005

1007-7294（2015）08-0919-08

2015-03-14

国家重大科技子课题专项（2011ZX05026-006-06）；创新研究群体基金资助（50921001）

赵小西（1987-），男，硕士研究生；

阮诗伦（1976-），男，副教授，硕士生导师，E-mail:ruansl@dlut.edu.cn。