随机面激励的非规则声腔自噪声计算方法研究

俞孟萨，白振国，吕世金（中国船舶科学研究中心，江苏 无锡 214082）

随机面激励的非规则声腔自噪声计算方法研究

俞孟萨，白振国，吕世金
（中国船舶科学研究中心，江苏 无锡 214082）

舰船声呐罩以及舱室、车厢等常见的非规则声腔受湍流边界层脉动压力随机面激励产生的水（气）动力噪声，已经或将成为声呐自噪声和舱室噪声的主要成因。文中以一个非规则形状的三维声腔为例，考虑声腔结构振动与内外声场的耦合，采用虚拟膜技术和集成模态法以及功率谱密度概念，建立了声腔受湍流边界层脉动压力随机面激励的自噪声计算模型和方法。数值计算分析表明：虚拟膜技术和集成模态法可用于舰船声呐罩以及列车和汽车车厢等非规则声腔自噪声计算的声学建模，预报声腔内部水动力噪声或气动力噪声的低中频分量，具有数值方法能够模拟复杂形状声腔和解析方法相应的声振耦合方程维数少的优点。

随机面激励；非规则声腔；自噪声计算

0 引 言

常见的非规则形状声腔有列车和汽车车厢、船舶舱室，以及为了避免“伪声”直接干扰而在舰船声呐基阵外面配置的声呐罩。舰船航行以及列车和汽车行驶时，声腔弹性结构在表面湍流边界层脉动压力激励下振动，并在腔内产生水（气）动力噪声场，随着舰船、列车和汽车速度的提高以及机械噪声的有效控制，它已经或将成为声呐自噪声和舱室噪声的主要成因。声腔在湍流边界层脉动压力下产生的腔内自噪声，涉及两个基本问题：一是声腔结构振动与内外声场的耦合，二是随机面分布激励。

声腔自噪声计算和预报历来是结构声辐射研究的一个重要分支。Dowell[1]利用Green公式和模态迭加法创立了求解声腔内部声场和腔壁振动的声弹性基础；Oldham[2]建立了矩形腔内外声场的计算模型；Cheng[3]采用Rayleigh-Ritz法建立了有限长圆柱壳和端板振动与内部声场耦合的运动方程；Kubota 和Dowell[4]在高频段采用渐近模态法对声腔模态函数进行空间平均处理，得到声压空间均方值的近似表达式；Missaoui和Cheng等人[5]发展建立了集成模态法研究有内部甲板的有限长圆柱壳结构振动与内部声场的耦合问题；Wu和Chen[6]提出了区域覆盖法求解复杂形状腔体内部声场；Petyt和Lim等人[7]采用变分原理建立了任意形状声腔结构振动与内部声场耦合的有限元求解方法。这些研究虽然考虑了声腔结构与内外声场的耦合或仅与内声场的耦合，但激励方式则为简谐点力或点声源。针对湍流边界层脉动压力随机面激励的情况，声腔自噪声研究一般都采用简化的规则声腔模型，Maidanik[8]建立了无限大平行声腔受湍流边界层脉动压力激励的内部噪声场计算模型；文献[9]采用平行声腔模型研究了夹芯复合结构腔壁受湍流边界层脉动压力激励产生的腔内自噪声；Rao[10]建立了矩形腔受湍流边界层脉动压力面激励的模型，研究舰船声呐自噪声；文献[11]采用波数--频率谱概念和随机场统计分析方法，建立了细长圆柱壳内部自噪声计算模型；Han等人[12]采用能量流法求解以能量密度为参数的平板振动方程，预报矩形腔内部声压均方值。为了求解声腔湍流边界层脉动压力激励产生的高频噪声，Vassas[13]采用统计能量法建立矩形腔内部噪声的计算方法，文献[14]建立了集成统计能量法计算复杂形状的声腔自噪声。这些研究虽然针对湍流边界层脉动压力随机面激励的声腔问题，但不适用于解决非规则形状声腔的低中频噪声。

本文针对舰船、列车和汽车典型的非规则形状声腔受湍流边界层脉动压力随机面激励的情况，考虑声腔结构振动与内外声场的耦合以及非正交界面引起的声腔模态耦合声阻抗，采用虚拟膜技术和集成模态法以及功率谱密度概念，建立适用于非规则声腔低中频自噪声预报的计算方法。

1 理论模型

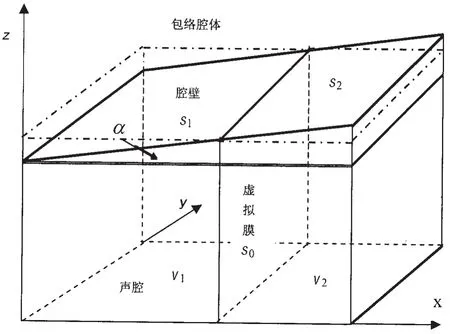
图1 非规则声腔及包络腔体Fig.1 Quasi-rectangular cavity and its envelope cavity

针对舰船、列车和汽车典型的非规则形状声腔的形状和结构特征，考虑一个非规则形状的三维声腔：其顶部为倾斜弹性薄板，倾角为α，其它壁面近似处理为刚性壁，声腔长、宽为lx，ly、高为lz和lz+lxtgα，如图1所示。声腔外部和内部充满特征声阻抗为ρ0C0的理想声介质，弹性薄板外表面受湍流边界层脉动压力激励。这种非规则声腔不能直接采用经典模态法求解腔内自噪声，而可以采用集成模态法求解，其基本思路是将非规则声腔内部空间分解为若干子腔体，采用几何形状与子腔体相近的规则包络腔体来模拟，并由规则包络腔体的模态函数迭加求解子腔体内部声场。鉴于图1所示的非规则声腔近似为准矩形腔，形状变化不大，为简单起见，将其分解为两个子腔体，记为子腔体1和2，体积分别为v1和v2，对应的顶部腔壁面积分别为s1和s2，围绕两个不规则子腔体作矩形包络腔体，其长、宽、高分别为设它们之间有一个虚拟弹性膜，面积为s0。

设声腔外部声压p0、子腔体1和2中声压p1、p2分别满足Helmohltz方程：

式中：k0=ω/C0，C0为声介质中的声速。

声腔顶部弹性薄板振动位移w满足小振幅弯曲振动方程：

式中：D，ms分别为弹性板弯曲刚度和面密度，ft为激励外力。弹性薄板上下表面应满足边界条件：

式中：ρ0为腔体声介质密度。

虚拟弹性膜振动位移V满足小振幅弯曲振动方程：

式中：Df，mf分别为虚拟弹性膜弯曲刚度和面密度。在虚拟弹性膜表面，声压与薄膜振动位移满足边界条件：

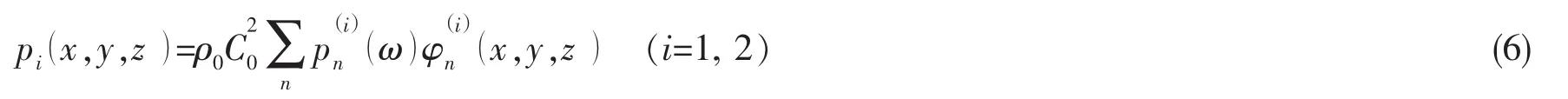
考虑子腔体内声场与弹性薄板和虚拟薄膜的耦合，利用Green公式，可以得到子腔体声场的模态声压耦合运动方程：

弹性薄板弯曲振动方程（2）式的模态解为

将（10）式代入（2）式，可得弹性薄板模态振动方程：

将（6）式代入（13）式、（10）式代入（9）式，分别得到腔内声场的广义模态力以及弹性板振动与腔内声场耦合的模态作用力：

设虚拟弹性膜振动方程（4）式的模态解为

将（18）式代入（4）式，可得虚拟膜的模态振动方程：

再将（21）式代入（19）式，且假设虚拟膜的质量和刚度为零，则（19）式左边取零值，可得到子腔体1 和2模态声压的连续方程：

最后将（16）、（22）式代入（7）式，得到子腔体声场与弹性薄板和虚拟薄膜振动耦合的模态运动方程，（14）、（15）式代入（11）式，则有弹性薄板与子腔体和外声场耦合的模态运动方程，连同（24）式一起表示为如下矩阵方程：

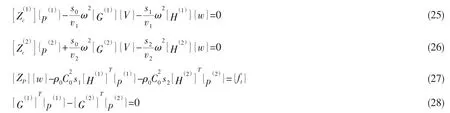
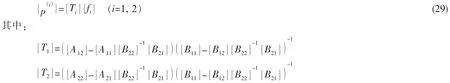
式中：［φi］分别为（x， y ，z）组成的行矩阵。

考虑到作用在声腔表面的湍流边界层脉动压力为随机面激励力，通过相关运算并计算声压功率谱密度，由（29）式可推导得到声腔自噪声的模态声压功率谱密度函数与模态激励力功率谱密度函数的关系[17]

其中：模态激励力功率谱密度函数由（32）式计算：

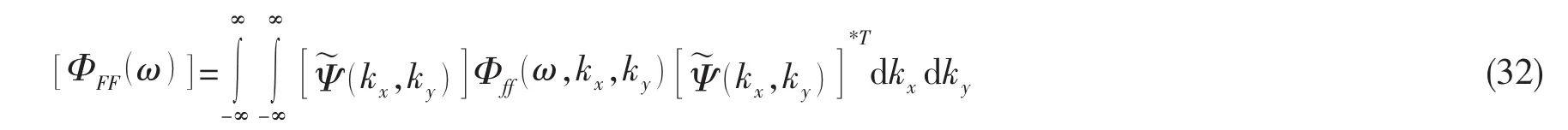
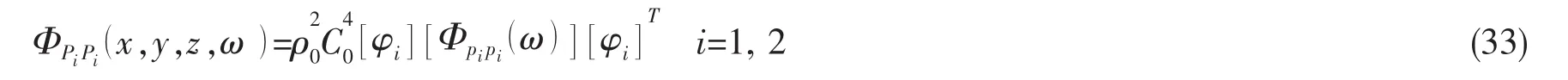
由上述模型可知：湍流边界层脉动压力激励弹性平板，通过平板振动模态和声腔模态的耦合在腔内产生噪声。声腔自噪声由不同模态的声压迭加而成，每一个声模态的贡献取决于弹性平板阻抗和声辐射阻抗、声腔声阻抗，以及弹性平板振动模态与空腔声模态的耦合关系和广义模态作用力。

［Ai j］，［Bij］（i,j=1,2）的表达式见附录B。

由（29）式得到的模态声压以及（6）式，可进一步计算声腔内部声场：

2 数值计算分析

本节依据前面建立的理论模型编制了计算软件，计算非规则声腔受湍流边界层脉动压力产生的自噪声，比较经典模态法（CMA）和集成模态法（IMA）的计算结果。计算选用Corcos[18]湍流边界层脉动压力波数—频率谱模型作为输入激励力谱。湍流边界层排挤厚度由文献[19]提供的公式计算，计算所取的声学参数见表1。数值计算分析分两种情况，第一种情况声腔弹性平板倾斜角为零，第二种情况倾斜角不为零。数值计算时，模态数取999，2 kHz以下频段声腔自噪声计算结果有很好的收敛性。

表1 声腔计算参数Tab.1 Calculation parameters of quasi-rectangular cavity

数值计算表明：在第一种情况下，弹性平板振动模态数与声腔声模态数互为奇偶数时，弹性平板与声腔产生声—振耦合，当激励频率等于声腔模态频率时，声腔模态声阻抗趋于无穷大，腔内声场与弹性平板阻抗无关，声腔产生共振现象；或者激励频率等于弹性平板和声腔耦合共振频率时，声腔也产生共振现象。图2给出了经典模态法计算的声腔自噪声，考虑弹性平板外场声辐射阻抗，声腔自噪声谱级减小10 dB以上，而且峰值宽度增加，对于水下声腔结构来说外场声辐射阻抗不能忽略。来流速度从5 m/s增加到10 m/s，声腔典型位置自噪声谱级整体性增加17～18 dB，符合水动力噪声强度随速度变化的规律，参见图3。

在计算频率范围内，统计能量法计算的声腔自噪声处于模态法计算结果的中间，800 Hz以上频段，模态法计算结果的平均值与统计能量法计算结果的偏差为1～2 dB左右，500 Hz以下频段，模态法计算的自噪声峰值起伏较大，两种方法计算结果的偏差达到5～10 dB左右，但总体趋势还是十分吻合，参见图4。模态法计算结果与试验测试结果也吻合较好，详见文献[21]。

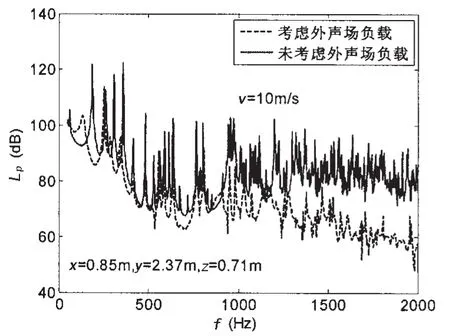
图2 声腔典型位置自噪声谱级Fig.2 SPL of typical position in acoustic cavity

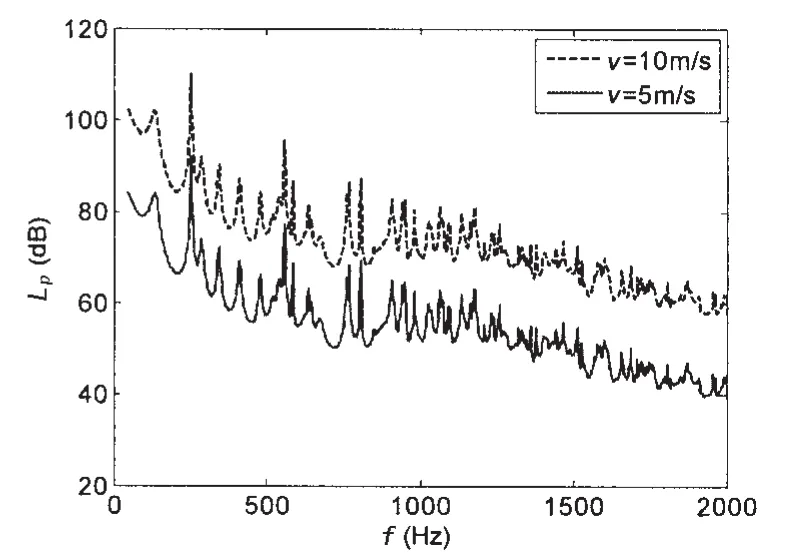
图3 流速对声腔自噪声影响Fig.3 Influence of velocity on the SPL of acoustic cavity

采用虚拟膜技术由集成模态法计算的声腔自噪声谱级由图5给出。集成模态法和模态法计算的声腔自噪声谱级十分接近，峰值位置基本重合，个别频率点上可能由于计算扫描频率不够精细使声压谱级有3dB左右的偏差。集成模态法计算的两个子腔体自噪声谱级随频率变化的规律相当一致，低频段峰值位置和幅值基本吻合，高频段略有差别，参见图6，而且基本不随虚拟膜的位置变化而改变，虚拟膜位置由x=1.1变化到x=1.7，声腔自噪声谱级峰值位置和幅值除了个别频率点相差3～5 dB外基本没有变化，参见图7。实际上，虚拟膜将声腔分为两个子腔体，采用包络腔体声模态求解声腔声场，这种方法类似动态子结构方法中的模态综合法[20]。模态综合法将子结构模态作为一组正交完备的函数族，构建整体结构振动响应，再由虚拟界面连续条件缩聚运动方程，求解过程与集成模态法比较相近。集成模态法中的虚拟膜将声腔分为两个子腔体，虽然使弹性平板与声腔的声振耦合关系变得复杂，但是它没有改变弹性平板与声腔的耦合特征。集成模态法与经典模态法求解矩形声腔自噪声的一致结果，表明了其原理的可靠性。

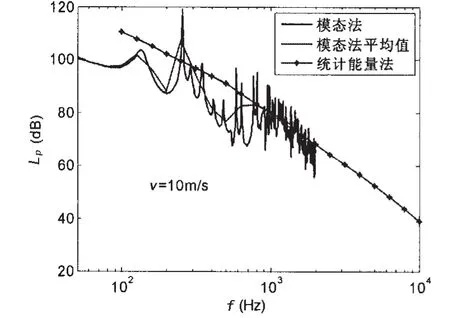
图4 CMA和SEA计算的声腔自噪声Fig.4 Averaged SPL of acoustic cavity calculated by CMA and SEA

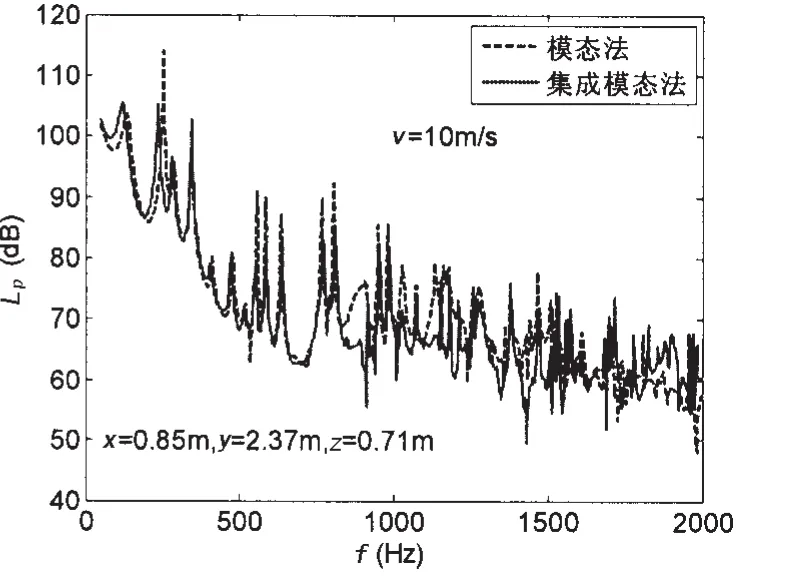
图5 CMA和IMA计算的声腔自噪声Fig.5 Averaged SPL of acoustic cavity calculated by CMA and IMA

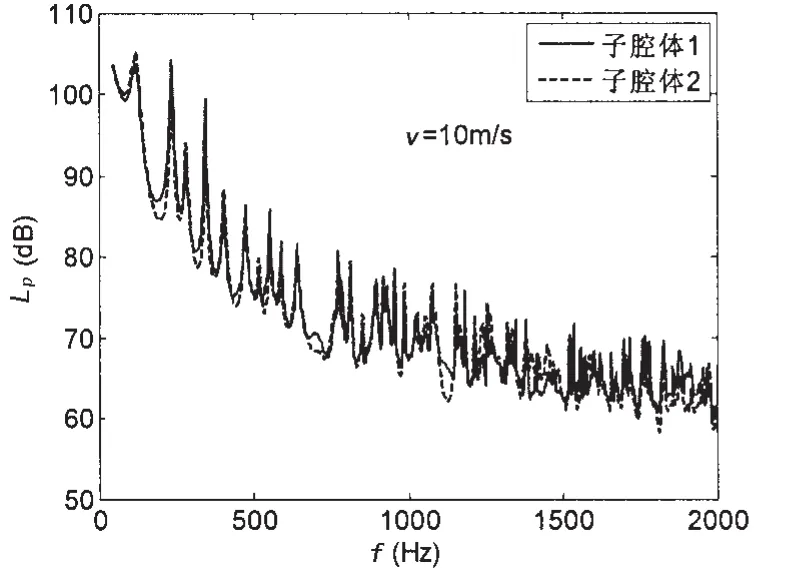
图6 IMA计算的子腔体自噪声比较Fig.6 Averaged SPL of two sub-cavity calculated by IMA

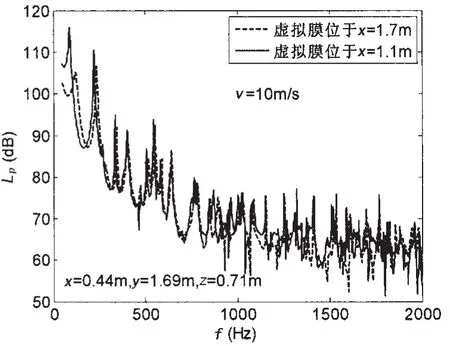
图7 虚拟膜位置对声腔自噪声的影响Fig.7 Influence of virtual-membrane location on typical position in acoustic cavity

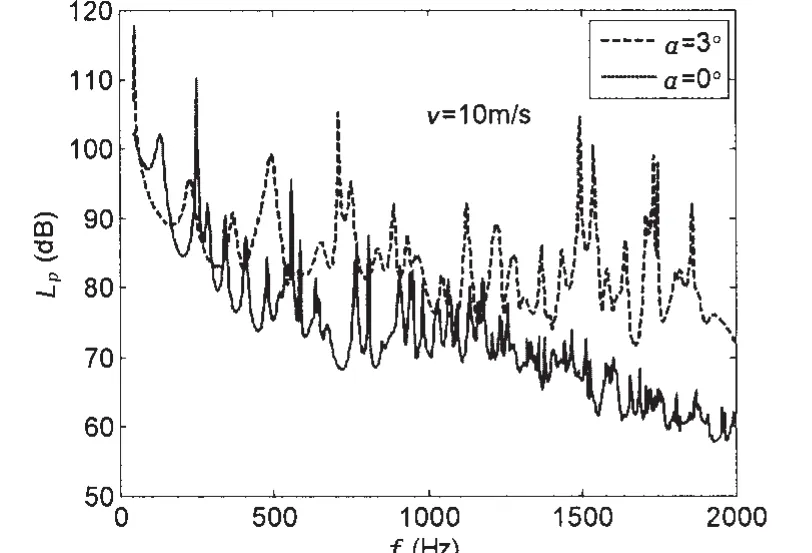
图8 弹性平板倾斜角对声腔自噪声影响Fig.8 Influence of leaning acoustic window on the averaged SPL of acoustic cavity

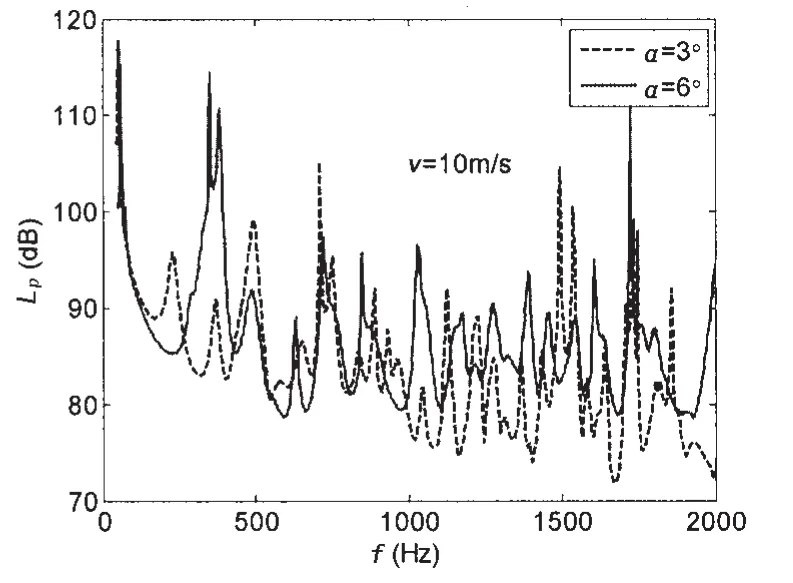
图9 弹性平板不同倾斜角对声腔自噪声影响Fig.9 Influence of different leaning acoustic window on the averaged SPL of acoustic cavity

在第二种情况下，因为声腔声阻抗由腔体模态声阻抗以及声腔几何形状与包络腔体模态函数的非正交性引起的模态耦合声阻抗两部分组成。模态耦合声阻抗减弱了弹性平板与声腔耦合所要求的模态选择性，对声腔自噪声的影响较明显，且与弹性平板的倾斜角有关。模态耦合声阻抗对声腔声场的影响取决于它与腔体声模态阻抗的相对大小，腔体共振时，腔体模态声阻抗很小，模态耦合声阻抗的作用不可忽略。从附录A中模态耦合声阻抗的计算表达式可知，弹性平板倾斜角对高阶声模态的模态耦合声阻抗影响较大。图8和9给出了弹性平板不同倾斜角时声腔典型位置自噪声谱级的比较。倾斜角α=3°和α=6°时，考虑了模态耦合声阻抗，在1 kHz以下频段声腔自噪声谱级出现新增峰值，1 kHz以上频段自噪声谱级峰值增高10 dB左右。声腔模态耦合声阻抗加强了弹性平板振动与声腔共振模态和高阶声模态的耦合，使声腔自噪声谱级增大。

3 结 语

以一个非规则形状的三维声腔为例，考虑声腔结构振动与内外声场的耦合，采用虚拟膜技术和集成模态法以及功率谱密度概念，建立了声腔受湍流边界层脉动压力随机面激励的自噪声计算模型和方法。数值计算分析表明：集成模态法与经典模态法和统计能量法计算的矩形声腔自噪声谱级吻合，虚拟膜位置的选取基本不改变集成模态法的计算结果，非规则声腔模态耦合声阻抗加强了弹性平板振动与声腔共振模态和高阶声模态的耦合，使腔内自噪声增大。因此，针对舰船、列车和汽车典型声腔的形状和结构特征进行声学建模，可以将虚拟膜技术和集成模态法推广用于舰船声呐低中频自噪声的水动力噪声分量以及列车和汽车车厢低中频噪声的气动力噪声分量预报。这种方法不仅可以近似模拟复杂形状声腔，而且相应的声振耦合方程的维数远小于有限元和边界元方法建立的声振耦合方程，兼有解析解和数值解的优点。

[1]Dowell E H,Gorman G F,Smith D A.Acoustoelasticity:General theory,acoustic natural modes and forced response to sinusoidal excitation including comparisons with experiment[J].J Sound and Vibration,1977,52(4):519-542.

[2]Oldham D J,Hillarby S N.The acoustical performance of small close finite enclosures,Part 1:Theoretical modes[J].J Sound and Vibration,1991,150(2):261-281.

[3]Cheng L.Fluid-structural coupling of a plate-ended cylindrical shell:Vibration and internal sound field[J].J Sound and Vibration,1994,174(4):641-654.

[4]Peretti L F,Dowell E H.Asymptotic modal analysis of a rectangular acoustic cavity excited by wall vibration[J].AIAA Journal,1992,30(5):1191-1198.

[5]Missaoui J,Cheng L.A combined integro-modal approach for predicting acoustic properties of irregular-shaped cavities[J]. J Acoust.Soc.Am.,1997,10(6):3313-3321.

[6]Wu J H,Chen H L.A method to predict sound radiation from an enclosed multicavity structure[J].J Sound and Vibration, 2001,249(3):417-427.

[7]Petyt M,Lim S P.Finite element analysis of the noise inside a mechanically excited cylinder[J].Inter.J for Num.Math.in Eng.,1978,13:109-122.

[8]Maidanik G.Domed sonar system[J].J Acoust.Soc.Am.,1968,44(1):113-124.

[9]Yu Mengsa,Li Dongsheng.Design of sandwich acoustic window for sonar dome[J].ACTA.Acustica,2005,30(5):427-434. [10]Rao V B.Prediction of flow induced noise of a ship’s sonar dome[J].UDT’98,1998:69-72.

[11]Tang Weilin,Wu Yi.Inter noise field of a viscoelastic cylindrical shell excited by the TBL pressure fluctuations:I.production mechanism of the noise[J].Acustica,1997,22(1):60-69.

[12]Han F,et al.Prediction of flow-induced structural vibration and sound radiation using energy flow analysis[J].J Sound and Vibration,1999,227(4):685-709.

[13]Vassas M.Evaluation of flow noise on a hull mounted sonar array[J].UDT’99,1999:356-359.

[14]Yu Mengsa,Zhu Zhengdao.Calculation of hydrodynamic component of sonar self noise by integro-SEA method[J].Journal of Ship Mechanics,2007,11(2):273-283.

[15]Li Y Y,Cheng L..Modifications of acoustic modes and coupling due to leaning wall in a rectangular cavity[J].J Acoust. Soc.Am.,2004,116(6):3312-3318.

[16]Davies H G.Low frequency random excitation of water-loaded rectangular plates[J].J Sound and Vibration,1971,15(1): 107-126.

[17]俞孟萨.舰船声呐罩的随机声弹性理论模型[C]//第十一届全国船舶水下噪声学术讨论会论文集.中国西安,2007.

[18]Graham W R.A comparison of models for the wave number-frequency spectrum of turbulent boundary layer pressures[J].J Sound and Vibration,1997,206(4):541-565.

[19]Schlichting Dr H.Boundary Layer Theory[M].Translated by Dr.Kestin J,McGraw-Hill Book Company,1979.

[20]殷学纲,等.结构振动分析的子结构方法[M].北京:中国铁道出版社,1991.

[21]Liu Xiaobin.Prediction and test of cavity’s hydrodynamic selfnoise induced by turbulent boundary layer[J].Acustica,Employed.

附录A：声腔模态耦合声阻抗

设包络腔体的声模态函数为

腔体x=0，lx；y=0，ly；z=0等五个表面，模态函数的法向导数为零，只有z=lz+xtgα面上模态函数的法向导数不为零。（7）式中声腔模态耦合声阻抗为

将（A1）式及其导数代入（A2）式，积分得到声腔模态耦合声阻抗：

附录B:矩阵表达式

Calculation of self noise in an irregular acoustic cavity under random surface excitation

YÜ Meng-sa,BAI Zhen-guo,LÜ Shi-jin
(China Ship Scientific Research Centre,Wuxi 214082,China)

The hydrodynamic(aerodynamic)noise,which is induced by random pressure fluctuation beneath the turbulence boundary layer,has been becoming the main contribution to self-noise of those cavities such as sonar self-noise and cabin noise.In this paper,to analyze the sound field in those cavities which are excited by the random pressure fluctuation on the flexible surface,the virtual elastic membrane technique and modal analysis method are adopted,the coupling effect of the structural vibration and the interior and exterior acoustic field is considered,the integral-modal analysis approach is used,and the power spectrum density and coupling impedance of the acoustic modes produced by the non-orthogonal interface are deduced.By all of these,the mathematical physical model is established and the hydrodynamic noise of a sonar dome is numerically computed.And the numerical analysis results show that the virtual elastic membrane technique and the integral-modal analysis approach can be effectively used to predict the sound field in varied irregular acoustic cavity in low and middle frequency range.This method has the advantages of the numerical method,which can simulate the complicated acoustic cavity and the less dimension of the analytical method of corresponding acoustic coupling equation.

random surface excitation;irregular acoustic cavity;calculation of self noise

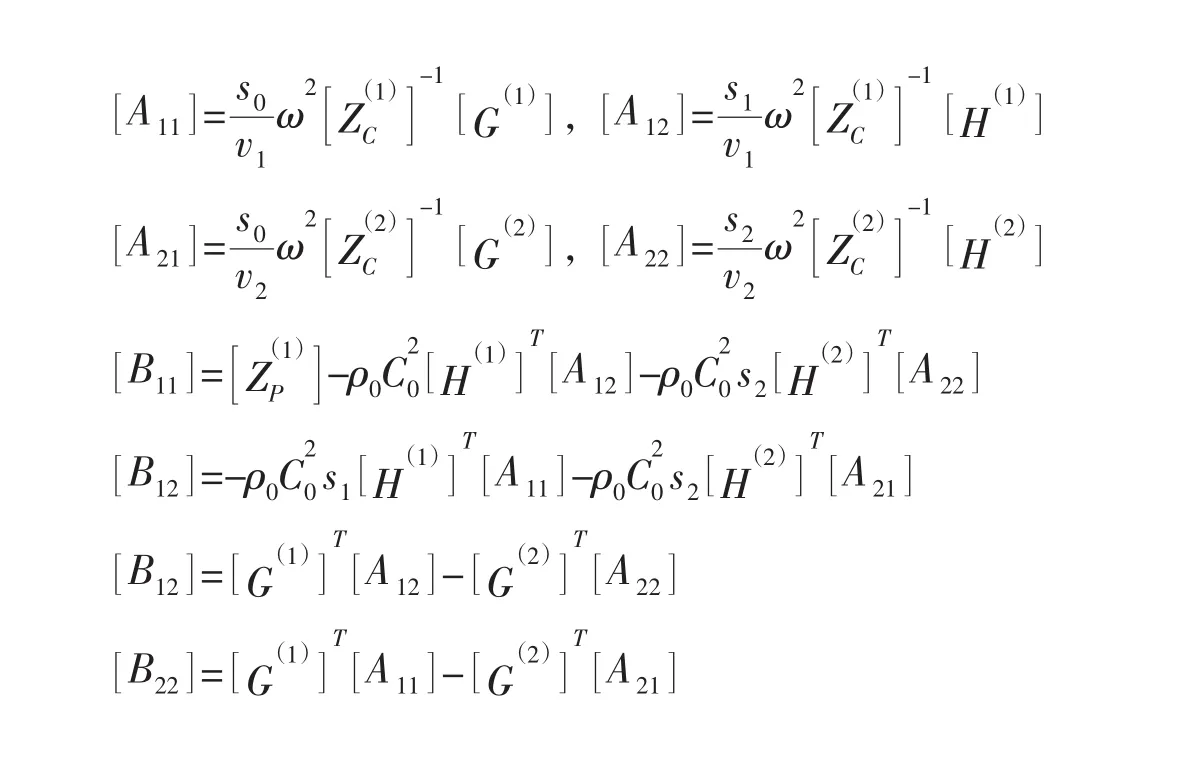
TB52+9

A

10.3969/j.issn.1007-7294.2015.08.015

1007-7294（2015）08-1001-10

2015-05-05

俞孟萨（1960-），男，研究员，E-mail:yumengsa@sohu.com；白振国（1982-），男，高级工程师。