基于MOGA的潜器快速性和操纵性综合优化研究
杨卓懿,宋磊
(山东交通学院船舶与海洋工程学院,济南250000)
基于MOGA的潜器快速性和操纵性综合优化研究
杨卓懿,宋磊
(山东交通学院船舶与海洋工程学院,济南250000)
基于Pareto解的多目标优化方法NSGA-II应用至潜器的快速性与操纵性综合优化设计之中。通过回转体潜器阻力性能的数值计算结果建立了阻力的近似计算模型,并与系列模型试验结果进行了比较;通过估算潜器的水动力系数,根据水平面线性运动方程得出水平面操纵运动稳定性和机动性的衡准指标。优化后,得到了阻力与回转直径的Pareto最优解的散点图,设计者可针对不同需求的潜器,从中进行选择,保证了Pareto最优解对应的每一艇型设计方案在满足操纵性要求下阻力最小,或在该阻力值的条件下操纵性最优。
潜水器;快速性;操纵性;Pareto解;多目标优化
0 引言
在潜器初步设计阶段,设计者能够综合考虑快速性、操纵性的要求,找到艇型参数、主尺度和操纵面参数的最优组合解集,并拥有足够设计决策权,才能保证潜器具有最优的航行性能。多学科与多目标优化提供了一种用于解决此类问题的手段,这也是舰艇设计领域的重要发展方向。从目前国内外的研究来看,舰艇的多目标优化由于更接近实际工程问题,正逐渐成为新的研究方向。如Peri、Tahara等[1-3]开展了高速双体船阻力与耐波性优化。杨松林等[4]利用线性加权求和的方法将多目标优化问题转化为单目标优化问题,进行了水面船的快速性和操纵性优化。庞永杰等[5]将阻力和排水量作为潜器概念设计阶段的目标函数,给出了优化后的Pareto解集。李学斌等[6]针对潜艇设计也做过相关研究。
基于Pareto解的多目标优化[7]找到的是全部非劣解集合,为设计者提供了重要的设计信息,避免了传统多目标优化方法中目标函数线性加权时权值选取的主观性。因此,本文将基于Pareto解的多目标优化方法应用至潜器的快速性与操纵性综合优化设计之中。在操纵性数学模型建立时,依据了潜艇操纵性设计计算标准[8];在快速性数学模型建立时,由于阻力估算经验公式[9]的基础因子是细长比,无法反映出艇型形状参数对阻力的影响,因此本文根据回转体的CFD计算建立了阻力近似计算模型,并与系列模型试验结果进行了比较,证明本文建立的近似模型更适宜应用在优化设计之中。
1 计算问题表述及建模
以某水滴型回转体潜器为原型,该潜器直径为1.0 m,长度为5.5 m,排水量为3.0 t,尾舵尺寸为0.360×0.420 m,舵面积为0.302 4 m2。水滴型艇型的母线线型是由1/4可以调整指数的椭圆及一段可以调整指数的抛物线来描述的,其公式如下[9]:
艏部曲线方程:

艉部曲线方程:

式中:ns、nw分别为艏部和艉部的形状系数,代表了艏部和艉部的丰满度。Ls为艏段长度,Lw为艉段长度,D为中段直径。计算过程中,应考虑潜水器具有平行中体,长度为Lz,则用6个参数能完整表达水滴型艇型。
根据实际问题的考虑,设计了如下限制条件:
(1)舵面积及舵安装位置保持不变。本文对操纵性的优化,只考虑主艇体的机动性,因此选择的设计参数为艇型参数,舵面积保持不变。即在相同舵效的基础上,设计具有最优机动性能指标的潜水器。
(2)潜水器直径D保持1 m不变;排水量Δ不小于原型,即Δ≥3.0。因为直径D的尺寸通常根据耐压舱布置而确定,其他探测导航设备则尺寸较小布置灵活,排水量不小于原型可以满足总布置的要求。
本文建立的数学模型如下:

优化过程中的5个设计变量,如表1所示。

表1 设计变量列表Tab.1 The list of design variables
2 操纵性数学模型的建立
根据国家标准[8],潜器水平面内横准参数可以由如下公式计算得到:
(1)静不稳定系数
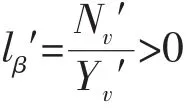
(2)动稳定系数

式中:lβ′为相对倾复力臂;为相对阻尼力臂。m′为无量纲质量;Nr为单位摇艏角速度r引起的力矩N;Nv为单位横向速度v引起的力矩N;Yr为单位摇艏角速度r引起的力Y;Yv为单位横向速度v引起的力Y。以上水动力导数的估算公式参考规范[8]。
(3)相对定常回转直径Ds

3 快速性数学模型的建立
3.1 阻力近似模型的建立
计算流体力学软件Fluent可以模拟复杂流体流动现象,得到高精度的流场的解,并能提供详细的流场信息,目前已经成为水动力分析的重要工具。水滴型艇型具有6个控制参数,单次阻力数值时间约3小时,为获取足够多且具有代表性的样本点,本文针对5 kns航速安排计算了40次拉丁方试验设计[10],得到排水体积V与湿表面积S、阻力F的40次CFD计算结果。根据试验设计,在Fluent中完成不同艇型的阻力数值计算,根据最小二乘法原理建立总阻力的4阶RSM(response surface model,RSM)模型。图1为根据试验设计完成艇型阻力近似模型建立的流程图。

图1 近似模型建立过程Fig.1 Process of setting up the approximate model
首先建立水滴型艇型的型值计算程序,输出型值点,然后导入Gambit中完成潜器和流场域的建立。网格划分时,对流域进行分割,除艉部过渡处以外,进行了结构网格的划分,从而保证了计算的精度。输出网格文件.msh导入至Fluent中作详细的计算。建立模型过程中的每一步操作以命令流的形式记录在Gambit的日志文件中,并且在Gambit中可以通过直接导入Journal日志文件完成建模和网格模型的输出[11]。对于大量的相似的试验,可以借助于Journal日志文件,高效率地实现参数化建模。在Fluent中进行流体数值模拟计算,需要设置复杂繁琐的求解模型和边界条件,同样可以应用Fluent自带的journal文件,自动导入.msh文件,一次性完成求解模型、边界条件和计算步数等设置。
3.2 阻力近似模型精度的验证
为了验证阻力近似模型的精度,设计了系列潜器模型,在循环水槽进行了阻力试验。回转体艇体直径D为280 mm,平行中体长为734 mm,分别设计了2组艏部模型和艉部模型,具体尺寸如下。艏部系列模型为两组:①长度为280 mm;②长度为504 mm;艉部系列模型为两组:③长度为504 mm;④长度为784 mm。这样,系列模型试验共有4个组合,如图2所示,分别为:
第一组合:①+平行中体+③,总长为1 518 mm;
第二组合:②+平行中体+③,总长为1 742 mm;
第三组合:①+平行中体+④,总长为1 798 mm;
第四组合:②+平行中体+④,总长为2 022 mm。
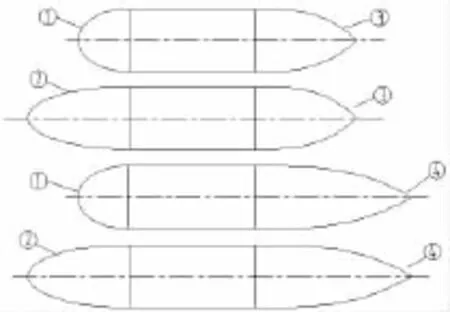
图2 系列模型的四个组合Fig.2 The four combinations of serial models

图3 系列回转体模型及阻力试验Fig.3 Serial revolving models and drag test
加工后的系列回转体模型及组合一在循环水槽内的直航阻力试验图片如图3所示。根据系列潜器模型试验结果做出的阻力曲线如图4所示。

图4 系列模型的阻力曲线Fig.4 Drag curves of serial revolving models
根据系列模型试验数据,在傅汝德假定的基础上,取来流速度为1.5 m/s的模型数据换算到近似模型适用区间内的实艇上。取流速1.5 m/s的主要原因是根据换算结果,实艇主尺度在近似模型适用区间内,同时模型的雷诺数≥(1.5~2.0)×107,满足船模边界层处于湍流状态的要求。根据四种组合的换算结果,取4个测试点,见表2,进行近似模型精度检验,分别将近似模型的近似解、CFD数值计算结果与根据试验结果换算得到的实艇阻力数据进行对比,如表3所示。
表3中,F1表示由试验值换算得到的实艇阻力;F2表示由CFD计算得到的阻力值;F3表示由4阶RSM计算得到的阻力值;F4表示由工程经验公式[6]计算得到的阻力值;ε2~ε4,分别表示以上计算值与试验值之间的误差,
由表3中数据可知,CFD计算值、4阶RSM模型、经验值与试验值的相对误差均值分别为7.64%,9.49%,37.01%。造成计算与试验值差别的原因除计算方法因素外,还包括基于傅汝德假定的换算误差、模型试验存在尺度效应等不可控制因素。4阶RSM模型能够正确反映艇型参数对阻力结果的影响且精度较高,而由经验公式得到的阻力值与试验值差别较大,并且经验公式的基础因子是细长比,无法反映出艇型参数对阻力结果的影响,在优化设计中不宜采纳。

表2 测试点数据Tab.2 The data of four test points

表3 不同计算方法下的阻力估算值Tab.3 The drag values calculated by different methods
4 基于Pareto解的多目标遗传算法
本文研究了NSGA-Ⅱ算法,并将其运用到艇型优化中,具体的技术策略如下:
(1)浮点数编码。涉及多维、高精度要求的连续函数优化问题时,浮点数编码可以有效地提高搜索效率。采用浮点数编码,即利用如下的线性变换:
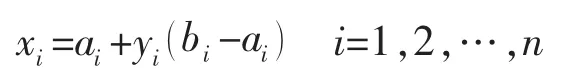
式中:bi,ai为变量的上下限,yi为[0,1]内的随机数。所有变量对应的xi构成问题解的编码形式。
(2)非支配排序方法。在选择操作执行之前,种群根据Pareto最优个体进行排序。首先,找出该种群中的所有Pareto最优个体,并赋予它们一个共享的虚拟适应度值,得到第一个Pareto最优层;然后,对种群中的其它个体继续按照Pareto最优个体进行分层,并赋予它们一个新的虚拟适应度值,该值要小于上一层的值,对剩下的个体继续上述操作,直到种群中的所有个体都被分层。这样,同一级别的个体具有相同的虚拟适应度值。
(3)基于排挤机制的小生境技术。为了确保种群的多样性,即希望解能够尽可能地分散在整个Pareto解集内,算法中引入了小生境技术对相同个体或类似个体的数量加以限制。计算在种群中给定点的周围个体的密度mi,它表示在个体i周围包含个体i本身但不包含其他个体的最小距离。当mi值较小时,表示该个体周围比较拥挤。这样,如果两个个体的非支配排序不同,取虚拟适应度值较高的个体;如果两个个体在同一级,取周围较不拥挤的个体。
5 优化结果及分析
在快速性与操纵性的多目标优化过程中,NSGA-Ⅱ算法控制参数设置为种群大小120,进化代数80和150,交叉概率0.85,变异概率0.1。图5给出了多目标优化过程中种群的进化趋势,从图5中看出,随着进化代数的增加,种群向着Pareto最优前沿逼进。图6给出了阻力和回转直径的Pareto最优解的散点图,进化代数达到80时,种群分布图已经初步表示出了Pareto前沿,当进化代数达到150时,种群分布图已经表示出了明显且均匀的Pareto前沿。
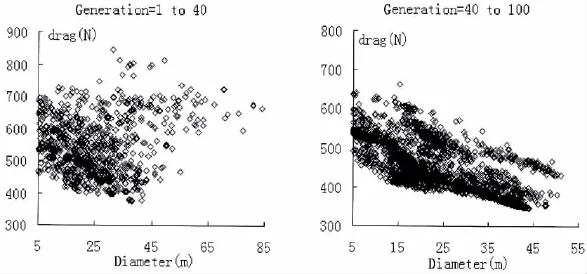
图5 快速性与操纵性优化的进化趋势图Fig.5 Evolutionary trend of resistance and manoeuvring optimization
在最终获得的Pareto最优解集中任意取4点,No.1和No.4靠近Pareto前沿的两端,分别表示有较为极端的操纵性能最优方案和阻力性能最优方案;No.2和No.3靠近中间,表示均衡考虑操纵性能和阻力性能的最优方案。表4中给出了4种具体设计方案对应的艇型参数值。从表4中可以看出,增加首尾段长度、减少平行中体段长度,即排水量满足约束条件下,增加细长比,增加潜水器的绝对长度,可以引起阻力的减小以及相对回转直径的增加。设计时,可以将所有的Pareto前沿对应的设计方案记录下来,针对不同需求的潜器,从中进行选择。

表4 Pareto解集中的四个设计方案Tab.4 The four results of Pareto optimal solutions

续表4
表4中,y1表示排水体积;y2表示细长比;y3表示相对回转直径;y4表示阻力近似值。
6 结论
本文研究了基于多目标遗传算法的潜器操纵性与快速性综合优化设计,通过分析,得到如下结论:
(1)潜器快速性数学模型建立时,本文根据CFD数值计算建立了阻力近似模型,与系列模型试验结果进行比较后,证明文中建立的近似模型能够正确反映艇型参数对阻力结果的影响,且精度高于经验公式估算结果,更适宜应用在优化设计之中;
(2)与固定权重的多目标优化不同,本文可以得到阻力与回转直径的Pareto最优解的散点图。Pareto解集为设计人员提供了非常重要且大量的设计信息,设计人员可以根据设计问题的实际需要和自己的经验从中选择,能够保证Pareto最优解对应的每一潜器方案在满足操纵性要求下阻力最小,或者说该阻力值的前提下操纵性最优。
[1]Peri D,Campana E F.Simulation based design of fast multi-hull ship[C]//26th Symposium on Naval Hydrodynamics. Rome,Italy,2006.
[2]Tahara Y,Peri D,Campana E F,Stern F.Single and multi-objective design optimization of a fast multi-hull ship:Numerical and experimental results[C]//27th Symposium on Naval Hydrodynamics.Seoul Korea,2008.
[3]Tahara Y,Peri D,Campana E F,Stern F.Computational fluid dynamics based multi-objective optimization of a surface combatant[J].Marine Science and Technology,2008,12(2):95-116.
[4]董亮,杨松林.高速单体船快速性和操纵性综合优化混沌算法[J].江苏科技大学学报,2007,2,21(1):7-11. Dong Liang,Yang Songlin.Overall optimization of rapidity and maneuverability of high-speed monohull ship based on chaos algorithm[J].Journal of Jiangsu University of Science and Technology(Natura l Science Edition),2007,2,21(1): 7-11.
[5]杨卓懿,于宪钊,庞永杰,宋磊.基于多目标遗传算法的潜器外形优化设计[J].船舶力学,2011,8,15(6):874-880. Yang Zhuoyi,Yu Xianzhao,Pang Yongjie,Song Lei.Optimization of submersible shape based on multi-objective genetic algorithm[J].Journal of Ship Mechanics,2011,15(6):874-880.
[6]李学斌,潘治.潜艇概念设计阶段的多目标优化研究[J].海军工程大学学报,2008,4,20(2):56-60. Li Xuebin,Pan Zhi.Multi-objective optimization study on conceptual design of submarine[J].Journal of Naval University of Engineering,2008,4,20(2):56-60.
[7]Deb K,Pratap A,Agarwal S,et al.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[8]中华人民共和国国家军用标准GJB/Z205-2001.潜艇操纵性设计计算方法[S].北京:国防科学技术工业委员会, 2001.
[9]朱继懋.潜水器设计[M].上海:上海交通大学出版社,1992:114-116.
[10]Simpson T W,Lin K J,Chen W.Sampling strategies for computer experiments design and analysis[J].International Journal of Reliability and Applications,2001,2(3):209-240.
[11]齐恩伍,蒋丹,刘斌.前处理软件GAMBIT参数化建模功能增强研究[J].东华大学学报,2008.6,34(3):341-343. Qi Enwu,Jiang Dan,Liu Bin.The investigation of enhancing the preprocessor GAMBIT function of parametric modeling [J].Journal of Donghua University(Natural Science),2008.6,34(3):341-343.
Integrated design of resistance and manoeuvring performances for submersible based on MOGA
YANG Zhuo-yi,SONG Lei
(College of Naval Architecture and Ocean Engineering,Shan Dong Jiao Tong University,Jinan 250000,China)
The multi-objective arithmetic NSGA-II based on Pareto solution is investigated to deal with integrated design of resistance and manoeuvring performances for submersible.Approximation model of drag for serial revolution shapes is constructed by hydrodynamic numerical calculations,and the precision of response surface model is validated by compared with the result from experiment of serial models in circular flume.The appraisement criterion of stability and mobility are calculated from linear equation of horizontal movement by estimating hydrodynamic coefficients of submersible.After optimization,the scattered Pareto solution of drag and turning diameter is gained,and from these the designer can choose the reasonable one from the actual requirement which can ensure the minimum drag in this manoeuvring performance or the best manoeuvring performance in this drag value.
submersible;resistance;manoeuvring;Pareto solution;multi-objective optimization
U661.31
A
10.3969/j.issn.1007-7294.2015.05.007
1007-7294(2015)05-0526-08
2014-11-11
山东交通学院博士科研启动基金资助项目
杨卓懿(1983-),女,博士,讲师,E-mail:yangzhuoyi@hrbeu.edu.cn;宋磊(1981-),男,博士,讲师。

