船舶非线性横摇运动数值模拟研究

杨波，石爱国，王骁，吴明

（海军大连舰艇学院航海系，辽宁大连116018）

船舶非线性横摇运动数值模拟研究

杨波，石爱国，王骁，吴明

（海军大连舰艇学院航海系，辽宁大连116018）

非线性大角横摇运动是危害船舶安全的重要因素，也是船舶水动力学关注的热点及难点问题。文章采用CFD方法，对某型驱逐舰船模在不同波长规则波中横浪航行时的横摇运动进行了数值模拟。通过与水池实验比对，数值仿真得到的稳定横摇幅值与实验值的误差在10%左右。同时，数值模拟证实了非线性横摇的两种典型特征—“多值”及“跳跃”现象。数值模拟结果表明，CFD方法可作为研究船舶非线性横摇运动的有效手段。

船舶；耐波性；非线性横摇；CFD

0 引言

横摇运动与船舶航行安全密切相关，往往是导致船舶倾覆的重要原因，因此一直是船舶耐波性研究所关心的问题。但由于横摇运动的复杂性，目前尚无准确的理论预报方法。工程应用中，一般采用基于实验获得的经验及半经验公式对计算结果进行修正[1]。

近年来，计算流体力学方法（Computational Fluid Dynamics，简称CFD）在船舶水动力研究中显示出了巨大潜力，并逐步应用于船舶的耐波性研究，而船舶的横摇运动是其中的热点之一，国内外许多学者进行了相关研究：Robert和Pablo等[2]对DTMB5512船模（带/不带舭龙骨）的强迫横摇及横摇衰减运动进行了数值模拟，并进行了详细的不确定度分析，分析结果表明数值模拟达到了较高精度；国内的张怀新[3]通过求解N-S方程，对Series 60船模不同位置的二维剖面的横摇流场进行模拟，得到了不同剖面的漩涡形状并计算了相应的横摇阻尼；黄昊等[4]基于FLUENT软件，对Series60船模的横摇二维剖面绕流进行了数值模拟，计算了横摇阻尼；朱仁传等[5]基于FLUENT软件，对实尺度的集装箱船S175的二维剖面横摇绕流进行数值模拟，通过数值模拟结果计算得了附加质量和阻尼系数；纪东方和朱良生[6]利用FLUENT软件对某一无航速驳船的二维剖面在静水中的自由横摇衰减运动进行了数值模拟，计算了横摇固有周期和阻尼系数；黄常青等[7]利用FLUENT软件对某型起重船的强迫横摇运动进行了数值模拟，并计算了相应的阻尼系数。

上述研究多限于船舶在静水中的横摇衰减及强迫横摇运动模拟，且国内的研究多限于二维或简单船型，对复杂线型船模在波浪中的横摇运动，尤其是非线性大角横摇运动尚无涉及。本文基于FLUENT平台，对其进行二次开发，首次对驱逐舰船模横浪航行时的横摇运动进行了数值模拟。实验涉及多种波长，最大稳定横摇幅值超过30度，横摇运动呈现出明显的非线性特征。数值模拟结果与水池实验结果吻合良好，证实了本文方法在船舶非线性横摇预报方面的有效性及精度。

1 非线性横摇运动方程

舰船的在规则波中的横浪横摇运动方程可表示为下述形式：

本文阻尼力矩采用如下非线性形式：

式中：B1和B2为系数，B2=2Nφφ（2Nφφ为小角度横摇时的线性阻尼系数）。

复原力矩项采用如下形式：

式中：C1、C3、C5为系数，其中C1=Dh。

为得到解析解，对阻尼力矩及复原力矩进行线性化。阻尼力矩线性化采用能量相等法。设有阻尼系数与组成的线性阻尼力矩若要用线性阻尼力矩代换非线性阻尼力矩需要保证在相同时间内，两者耗散的能量相同（做功相同），即：

设非线性方程的解为：

将（5）式代入（4）式，经整理可得线性化的横摇阻尼系数：

复原力矩线性化采取的方法是对非线性项展开，略去部分高阶项。仍然采用（5）式表示的横摇解析解，复原力矩可表示为：

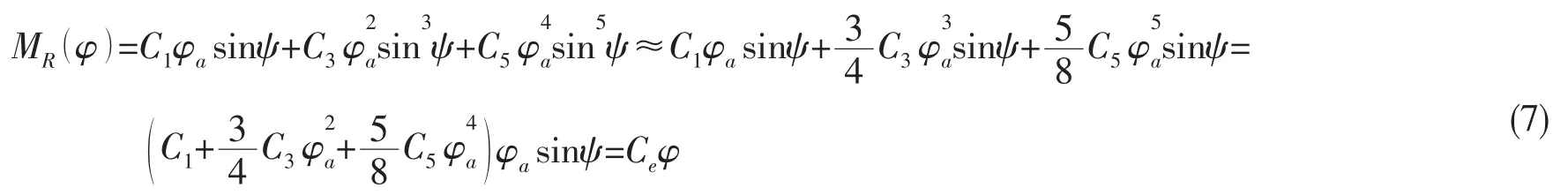
将（6）式、（7）式代入（1）式，并除以（Iφφ+ΔIφφ）得：

式中：2νe为无因次化横摇阻尼系数，ne为横摇固有频率，nφ为线性横摇时的固有频率。（8）式即为阻尼及复原力矩非线性时的横摇运动方程。

将（5）式代入（8）式并进行迭代求解，可得方程的解析解：

由（9）式可得稳定横摇幅值φa随波频ω的变化规律，即横摇幅频响应曲线。

2 控制方程

对船舶运动来说，可将水视作不可压缩粘性流体，其控制方程主要包括连续性方程、动量方程（NS方程）、湍流方程，各方程张量表示如下：

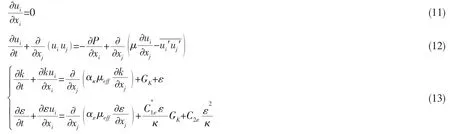
式中：xi、xj为笛卡尔坐标方向，i、j=1，2，3；ui、ui′为xi方向速度时均值、脉动值；P为压力；t为时间；μ为运动粘性系数；k为湍动能；ε为湍流耗散率

采用流体体积法（Volume of Fluid，简称VOF）模拟自由面，体积分数Cq的控制方程为：

式中：mpq为从q相传输到p相的质量；ρq为第q相密度；t为时间。

3 数值模拟方案

3.1 船模选择及实验参数

文献[8]对某驱逐舰船模在规则波中横浪航行时的系列横摇运动进行了水池实验研究，并采用ITTC的推荐方法对水池实验数据进行了不确定度分析，具有较高的可信度。为验证数值模拟方法精度，本文采用与文献中相同的船模及实验参数。该型驱逐舰型船模与实船比例为1：50，其参数如表1所示，型线图如图1所示。共进行20组实验，波频范围3.394≤ω≤5.459 rad/s，波高波长比H/A=1/30，实验参数如表2所示。

表1 船模参数Tab.1 Parameters of ship model

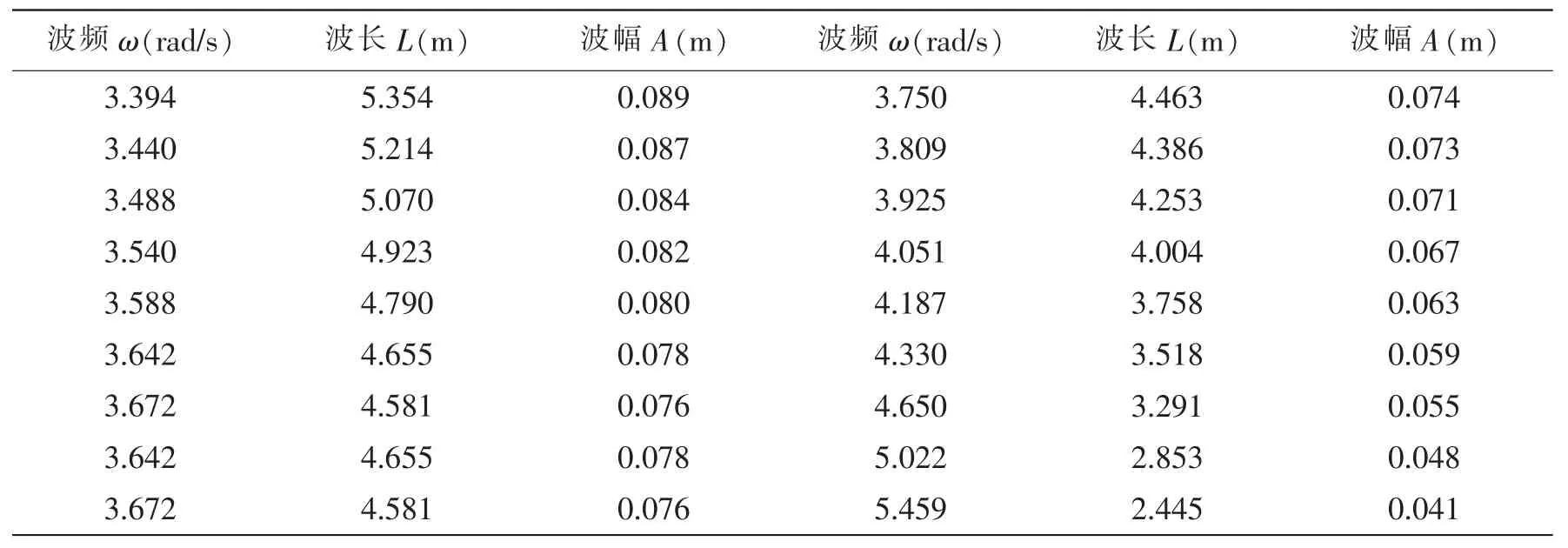
表2 实验参数Tab.2 Parameters of simulations

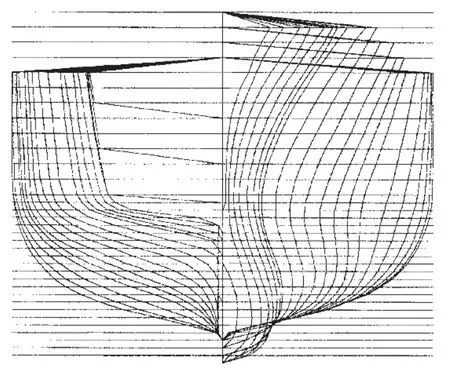
图1 船模型线图Fig.1 Body plan of the ship model

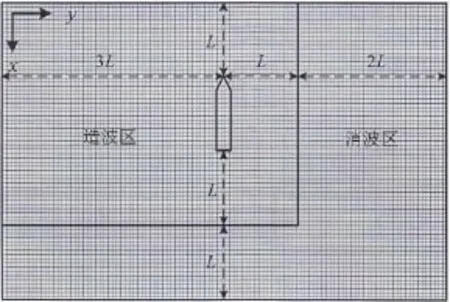
图2 计算域尺寸（顶视图）Fig.2 Scale of computational domain(top view)

3.2 计算域及网格划分

计算域设置为长方体，在船体后部及右侧（假设左舷来波）设有消波区。计算域尺寸为3L×5L×1.2L（长×宽×深，L为船长），其中水深为1L，具体尺寸如图2所示。对计算域进行分区处理，如图3所示，各分区网格划分情况为：

（1）船体近流场区域（Z1）：为船体表面到一个包裹船体的长方体之间的区域，长方体尺寸为1.5L×1.5B×1.5B（L为船长，B为船宽）；该区域生成非结构性网格，在船体表面布设20层边界层，船体面网格尺寸为0.01 m，该区域网格最大尺寸为0.02 m。

（2）与近流场区域等高的圆柱形区域（Z2），将Z1“包裹”在其内部，圆柱底面半径为2B，轴线为船舶横摇轴；该区域生成结构性网格，内边界网格尺寸及类型与Z1相同，外边界（底面及侧面）网格最大尺寸约为0.035 m。

（3）外流场区域（Z3）为除Z1、Z2之外的计算域。该区域生成结构性网格，在自由面处加密Z方向网格，以生成高质量波浪环境，Z网格尺寸为A/2（A为波幅），其余网格由自由面向上下渐疏。

设置船体仅作横摇运动，通过动网格技术实现。将Z1及Z2设置为刚体，随船体转动，Z3相对于坐标系保持静止，Z1、Z2与Z3的内部边界设置为interface，船模运动通过船体所受水动力驱动。

图3 计算域分区处理Fig.3 Multi-blocks of computational domain

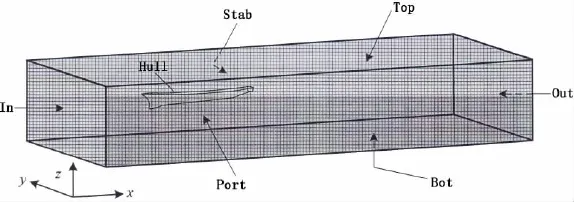
图4 边界名称Fig.4 Boundary conditions

3.3 边界条件

各边界条件名称如图4所示，具体设置如下（假设左舷来波）：

（1）入口边界（in，port）—速度入口，给定三个方向的波速及水的体积分数；

（2）出口边界（out，stab）—压力出口，设置静水压力；

（3）外边界（top，bot）—速度入口，给定三个方向流速（u=v=w=0）及水的体积分数（0）；

（4）船体（hull）—壁面，有剪切力无滑移。

4 数值模拟结果分析

本文数值模拟得到的各波频的稳定横摇幅值与水池实验值的对比如表3所示（CFD为仿真值，EXP为水池实验值）。从表中可以看出，仿真值与水池实验值的误差均在10%以内。

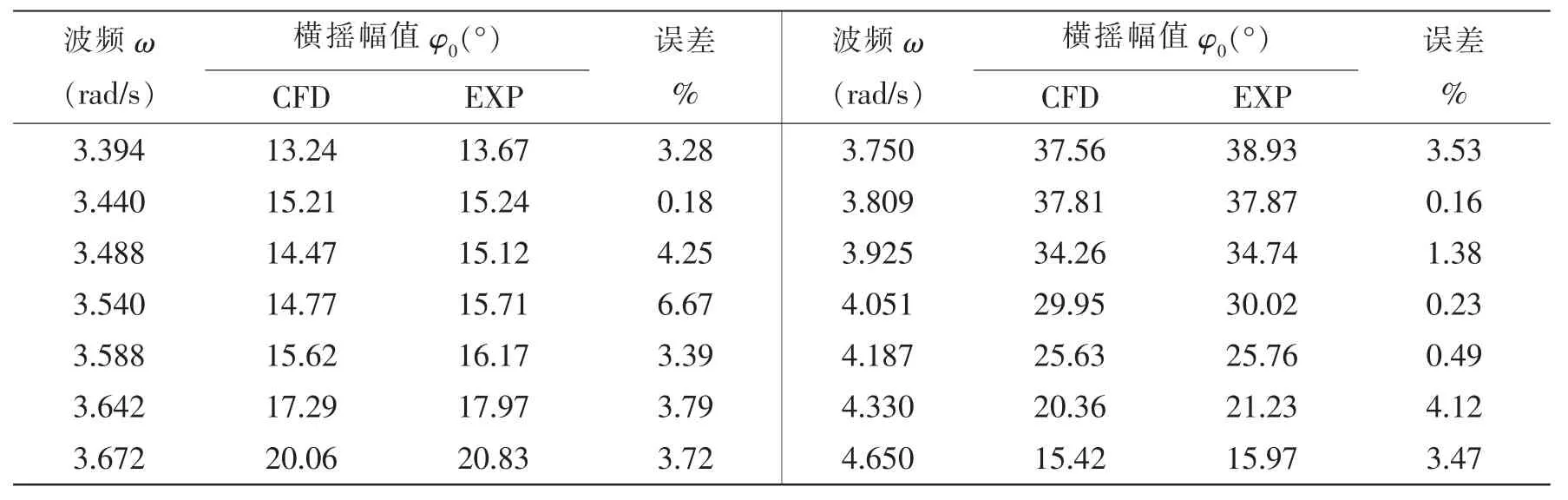
表3 横摇幅值Tab.3 Roll amplitude

续表3

4.1 “偏顶”现象

图5中虚线为船模的固有频率曲线，CFD（三角）为本文数值仿真值，THE（实线）为（9）式的理论解。从图中可以看出：

（1）本文数值模拟值随频率变化规律与理论解较为接近，且所捕捉到的横摇最大值及多值区所对应的频率范围，亦与理论解相似。这间接证明了本文数值模拟的可信度。

（2）幅频曲线分布于固有频率曲线两侧，且产生了非常明显的“偏顶”现象，固有频率曲线基本通过幅频曲线最大值点。

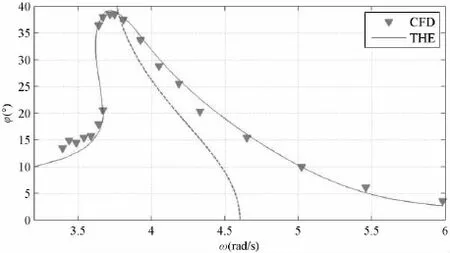
图5 幅频曲线Fig.5 Roll amplitude-frequency curve

4.2 多值及跳跃现象

从表3可以看出，当波浪频率ω=3.642和3.672时，对应2个稳定横摇幅值。图6为图5的局部放大图，从图中可以清楚地观察到多值区域。

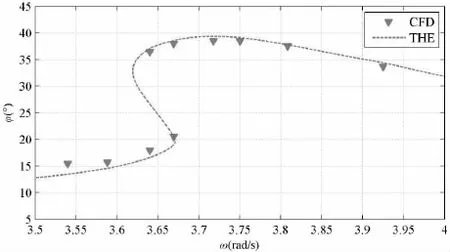
图6 多值区域Fig.6 Frequency domain of multi-amplitude

虽然存在多值区域，但是其频率区域非常小，大约在3.60～3.70 rad/s范围内；同时，在实验中发现，虽然在两个频率点产生了多值现象，但是其实现过程并不相同。下面通过仿真时历进行说明。

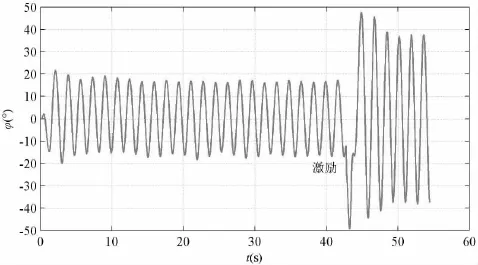
图7 横摇角时历图（ω=3.642 rad/s）Fig.7 Time history of roll angle(ω=3.642 rad/s)

（1）图7为ω=3.642 rad/s的横摇仿真时历图。在仿真开始时刻，通过已经生成好的横浪流场初始化横摇运动流场，船模很快进入稳定横摇状态，横摇幅值稳定在17.29°左右（见表3）。在t=42 s左右，对船加一瞬时激励，此激励幅值为稳定横摇力矩的10倍，作用时间为T/20（T为波浪周期）。这样船模会产生一个非常大的激励幅值，约为50°左右，大约经3～4个周期后，船模即进入另一稳定横摇状态，横摇幅值约为36°（见表3）。但是无论再对船模再次进行何种激励，船模也无法回到初始时的稳定横摇状态。

（2）图8为ω=3.672 rad/s的横摇仿真时历图，与图7采用相同的初始化方法。经过小幅振荡后，横摇角幅值稳定在37°左右。采用与图7相同的激励方法，横摇角振荡后仍然稳定在37°左右，也就是说，在此种工况下难以出现多值现象。

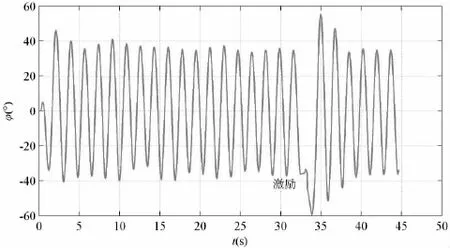
图8 横摇角时历图（ω=3.672 rad/s）Fig.8 Time history of roll angle(ω=3.672 rad/s)

（3）图9同为ω=3.672 rad/s的横摇仿真时历图，采用与图7相同的初始化方法。但是在计算开始阶段，约束船模不发生横摇运动；当t=5 s左右，去掉横摇约束，船模开始运动，在经过4～5个周期后，横摇幅值慢慢趋于稳定，此时横摇幅值为20°左右；稳定一段时间后加激励，此时船模很快稳定于另一横摇幅值，约为37°左右，出现多值现象。

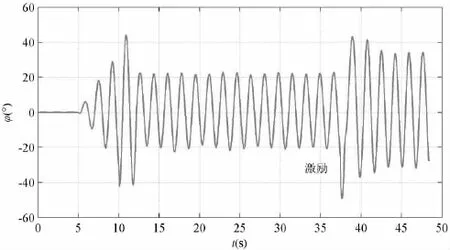
图9 横摇角时历图（ω=3.672 rad/s）Fig.9 Time history of roll angle(ω=3.672 rad/s)

从上述分析可以看出：

（1）虽然此型船模存在横摇多值区域，但是由于静稳性曲线及阻尼力矩的特点，产生多值的频段很窄，较难发生“多值”及“跳跃”现象。

（2）如果船舶在某一波频上会产生多值现象，初始较小横摇角的稳定状态很容易被外部激励改变，而稳定于较大的横摇角幅值；反之，较大横摇角的稳定状态则要稳定得多，不易变化。

（3）多值现象的出现及其状态特点，与船模的初始条件和扰动力矩特点密切相关，即使处于理论多值频段内，多值现象也不一定会出现。

5 结论

本文采用CFD方法，对某型驱逐舰船模在不同波长规则波中横浪航行时的横摇运动进行了数值模拟。数值模拟结果与水池实验结果吻合良好，稳定横摇幅值的误差在10%以内，证实了横摇幅频曲线的“偏顶”、“多值”及“跳跃”现象。上述模拟结果说明，采用CFD方法研究船舶的非线性横摇运动是可行的，且具有较高精度，可以作为理论研究及水池实验研究的有力补充。

[1]Chakrabarti S.Empirical calculation of roll damping for ships and barges[J].Ocean Engineering,2001,28:915-932.

[2]Wilson R V,Carrica P M,Stern F.Unsteady RANS method for ship motions with application to roll for a surface combatant[J].Computers&Fluids,2006,35:501-524.

[3]张怀新,刘应中,缪国平.船体各种剖面的横摇阻尼与漩涡的形状[J].水动力学研究与进展,2001,16(3):382-389. Zhang Huaixin,Liu Yingzhong,Miao Guo-ping.Vortex patterns and roll damping at various cross sections of ship[J]. Journal of Hydrodynamics,2001,16(3):382-389.

[4]黄昊,郭海强,朱仁传,缪国平.粘性流中船舶横摇阻尼计算[J].船舶力学,2008,12(4):578-573. Huang Hao,Guo Haiqiang,Zhu Renchuan,Miao Guoping.Computations of ship roll damping in viscous flow[J].Journal of Ship Mechanics,2008,12(4):578-57.

[5]朱仁传,郭海强,缪国平,余建伟.一种基于CFD理论船舶附加质量与阻尼的计算方法[J].上海交通大学学报,2009, 43(2):198-203. Zhu Renchuan,Guo Haiqiang,Miao Guoping,Yu Jianwei.A computational method for evaluation of added mass and damping of ship based on CFD theory[J].Journal of Shanghai Jiaotong University,2009,43(2):198-203.

[6]纪东方,朱良生.粘性流中船舶自由横摇衰减运动数值模拟[J].科学技术与工程,2009,9(23):7061-7065. Ji Dongfang,Zhu Liangsheng.Numerical simulation of ship free roll decay motion in viscous flow[J].Science Technology and Engineering,2009,9(23):7061-7065.

[7]黄常青,王学林,胡于进.基于CFD的起重船水动力系数数值模拟[J].中国机械工程,2011,22(17):2076-2079. Huang Changqing,Wang Xuelin,Hu Yujin.Numerical simulation of hydronamic coefficients of crane ship based on CFD [J].China Mechanical Engineering,2011,22(17):2076-2079.

[8]Alberto Francescutto,Giorgio Contento.Bifurcations in ship rolling:Experimental results and parameter identification technique[J].Ocean Engineering,1999,26:1095-1123.

Simulation of ship’s non-linear roll motion

YANG Bo,SHI Ai-guo,WANG Xiao,WU Ming
(Dept.of Navigation,Dalian Naval Academy,Dalian 116018,China)

Non-linear roll motion is a crucial factor in endangering ship’s security and a hot issue in ship’s hydrodynamics study.In this paper,ship’s roll motion in different regular beam sea waves is simulated. The simulation results show good agreement with the tank test results,and the error is less than 10%.The typical phenomena of nonlinear roll-‘multi-amplitude’and‘jumping’are also realized in the simulation. The simulation results show that CFD method can be an effective tool in studying ship’s non-linear motion.

ship;seakeeping;non-linear roll;CFD(Computational Fluid Dynamics)

U661.74

A

10.3969/j.issn.1007-7294.2015.05.005

1007-7294（2015）05-0509-09

2014-12-15

辽宁省博士科研启动基金项目（20111037）

杨波（1983-），男，博士研究生，E-mail：bisecond@163.com；

石爱国（1956-），男，教授，博士生导师。