桌式贴片机横梁的模态分析及拓扑优化设计

白俊峰，闫俊存，黄 勇

BAI Jun-feng1, YAN Jun-cun1, HUANG Yong2

（1.长春工业大学 机电工程学院，长春 130012；2.吉林省博安消防设备有限公司，长春 130000）

0 引言

上世纪60年代，表面组装技术 SMT（Surface Mounted Technology）就已经开始出现。经过几十年的发展，SMT已经成为了一门涉及机械、电子、计算机以及材料等多门学科的综合性技术。SMT的主要工作流程有点胶（或丝印）、贴装、固化、回流焊（或波峰焊）、清洗、检验等工作流程。贴装作为SMT中最主要的工序之一，精度要求极其严格，其工作任务主要由贴片机承担。

贴片机实际上是一种高精度、高速度的智能机器人，主要由机械系统和控制系统组成。其中机械系统主要有机壳、XYZ三轴运动系统、贴片头、机架、传送机构等；控制系统主要有视觉识别系统、定位系统以及各种传感器等。图1所示为贴片机单次贴装动作图。

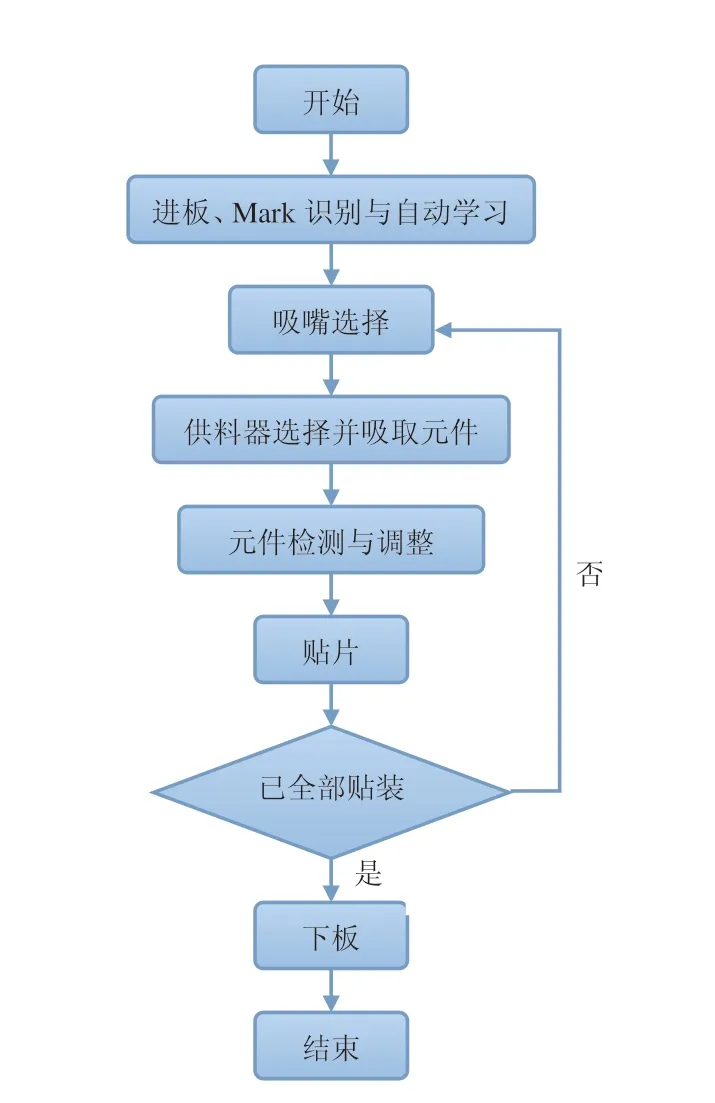
图1 贴片机单次贴装动作图

1 桌式贴片机横梁优化前有限元模型建立

横梁承载着桌式贴片机XYZ轴的运动，它的结构直接影响贴片机的贴装精度，是桌式贴片机最重要的构件之一。因此，贴片机贴装精度能否满足作业要求，与横梁的结构设计、结构分析以及结构优化有着很密切的关系。本文主要采用有限元方法对横梁结构进行模态分析，避免共振点；然后在此基础上对横梁结构进行拓扑优化，以保证贴片机贴装精度。桌式贴片机的整机结构如图2所示，其中横梁采用铸铝成型如图3所示。

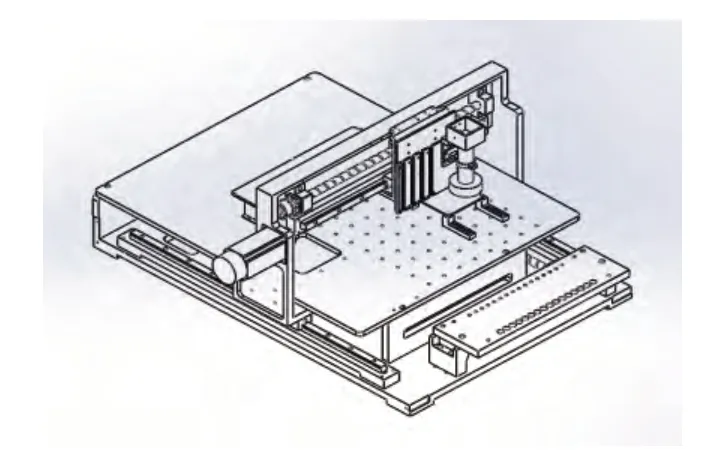
图2 桌式贴片机的整机结构

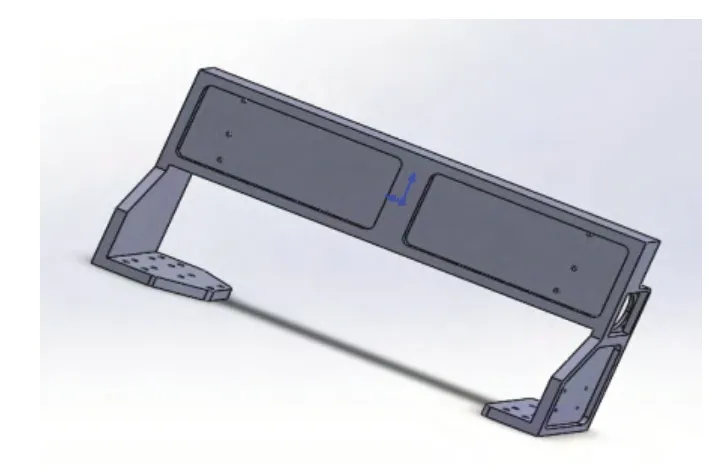
图3 桌式贴片机横梁

如上所述，横梁作为贴片机的关键部件，其有限元模型的建立也是分析横梁结构的关键环节，单元选择不准确、模型大小与实际不相符，都会产生错误的分析结果。为保证计算精度、达到实际应用标准，本文采用ANSYS有限元法对横梁进行分析，单元类型选用solid95实体单元，体积为：1.73×106mm3，质量为：4.7kg，杨氏模量：E=69GPa，泊松比为：0.33，材料密度为：2700kg/m3。网格划分采用等级为6级的智能网格划分，最终建立的有限元模型如图4所示。

图4 横梁有限元模型

2 横梁的模态分析

模态分析是工程中经常使用的分析方法，通过模态分析确定横梁结构的固有振型和频率，对横梁进行合理改善，避开共振频率；依据分析结果进行结构优化，优化结构应力集中部位，加强结构强度，延长结构使用寿命。

ANSYS有限元模态分析属于线性分析，所有的非线性特性将被忽略，其主要理论基础为振动理论分析方法。首先将模型结构进行网格划分，将实体单元数据离散化处理；然后依据有限元数值分析方法，建立线性微分方程组；最后求出所构建方程组的特征值以及特征向量。根据振动理论相关知识，得到横梁离散后的运动微分方程为：

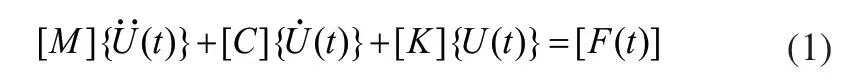
式中[M]为横梁结构的质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{U(t)}为位移向量；[F(t)]为激励矩阵。

对式(1)进行拉氏变换，可得：

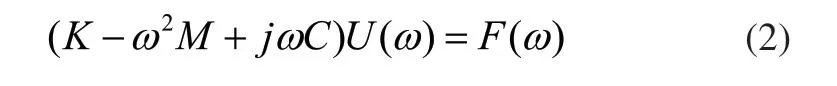
对于时不变线性系统某点的响应，可用各阶模态响应的线性之和表示，于是可以得到某点a的响应为：

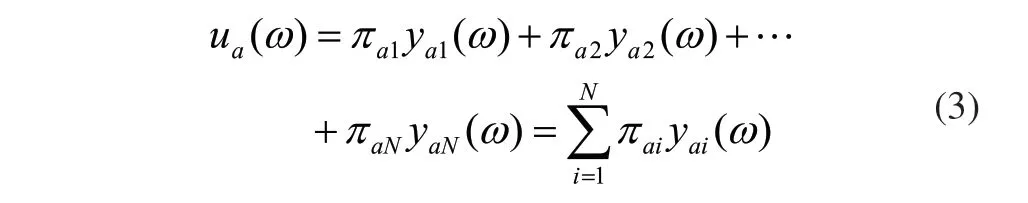
假设横梁有限元模型中的M个节点第i阶模态对应的振型系数组成的列向量为：则由这M个点所对应的全部模态振型系数矩阵为：

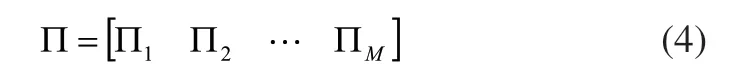
又设由这M个点组成的模态坐标矩阵为：

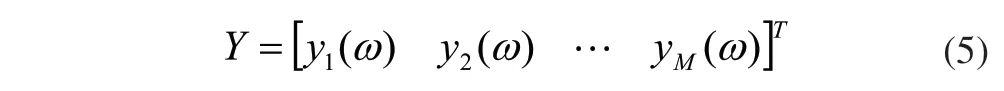
将式(4)、式(5)带入式(3)，可以得到结构的响应向量为：

此时，可以将式(2)改写为：

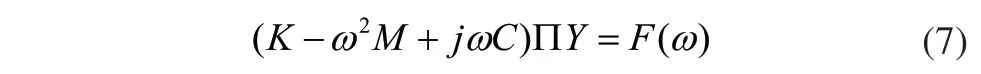
而在实际的模态分析中，阻尼对结构的固有频率以及振型的影响很小，可以忽略不计，且ANSYS软件测量结构的模态时一般不需要施加激励，此时式(2)特征方程为：

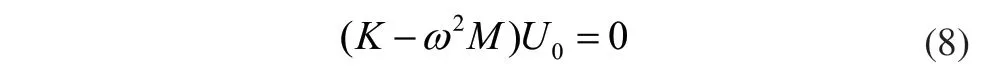
这样便可以求得横梁的固有频率计算公式：

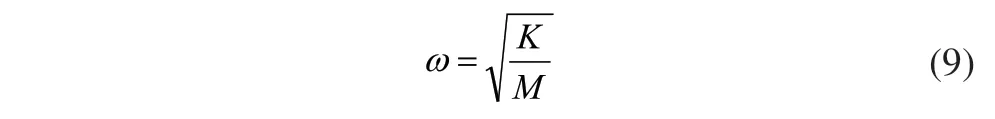
根据上面的计算原理，将上节建立的有限元模型载入ANSYS软件，计算横梁的前五阶模态频率及振型如表1所示，得到振型图如图5(a)～图5(e)所示。

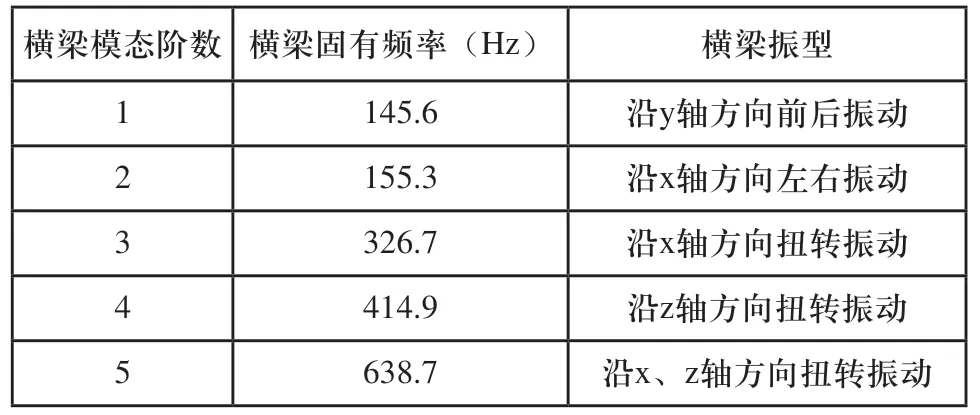
表1 横梁前5阶固有频率及振型

通过表1数据可以看出，横梁的一阶固有频率为145.6Hz，而系统所使用的伺服电机工作转速变化范围为0～3000r/min，即激励系统的工作频率变化范围为0～50Hz，此横梁结构固有频率明显大于激振频率，故不会发生共振。但是由于此结构质量较大为4.7kg，在桌式贴片机高速运行突然急停进行贴片的动作中，横梁的大质量引起的惯性作用，回使贴片头在贴装时发生偏移甚至可能出现错位的现象，因此进行拓扑优化，对横梁进行轻量化设计是非常必要的。

3 横梁的拓扑优化设计

拓扑优化设计是运用优化设计理论、数据处理方法、计算机辅助软件等工具，寻求材料最合理分配的一种设计理念，以达到结构最佳外观形式、最佳受力途径、结构最佳性能、结构最为轻量化的设计方法。

拓扑优化主要有三种方法：均匀法、变厚度法和密度惩罚法。本文中采用密度惩罚法来完成横梁的拓扑优化，其数学模型如下：

式(10)中 iρ 为单元相对密度；f为结构体积力；u为单元相对面积力；v0为结构初始定义体积；v*为删除的材料体积；Δ为删除材料质量所占比例；ε为密度惩罚法材料密度下限；Jj为优化后密度保持最初状态的单元。经过ANSYS拓扑优化计算，可以得到优化后单元密度变化情况如图6所示，横梁优化最终拓扑结构如图7 所示。

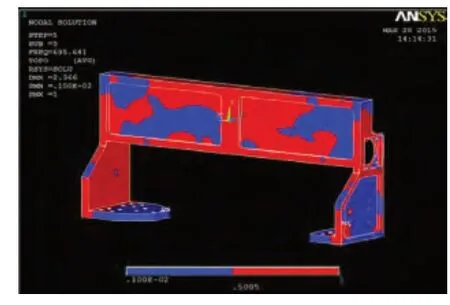
图6 优化单元密度变化图

图7 优化后拓扑结构

经测量，优化后计算得到横梁的质量为3.8kg，比优化前减少了19.1%，减小了惯性带来的贴装误差。

在实际的工程应用中，高阶模态对结构的影响很小，因此本文仅对横梁前五阶模态进行了模态分析，得出优化后横梁前五阶模态固有频率，以及优化后前两阶横梁应力图（优化后横梁模态固有频率与优化前的固有频率对比如表2所示，优化后前两阶应力分布图如图8、图9所示）。

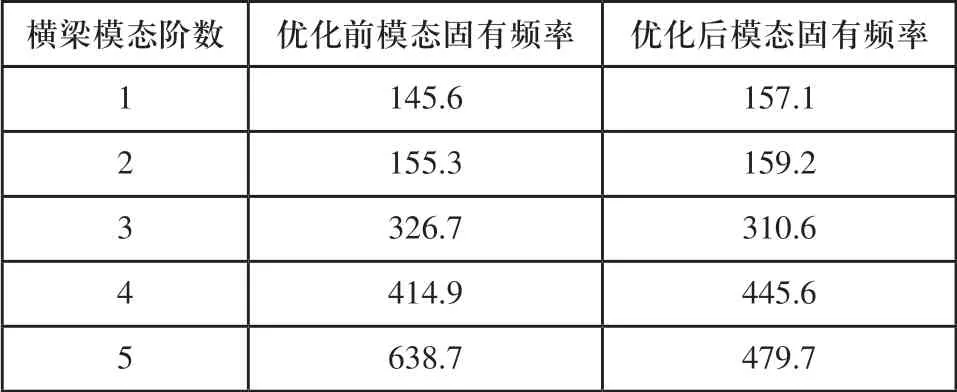
表2 拓扑优化前后固有频率对照表

图8 优化后横梁1阶应力图

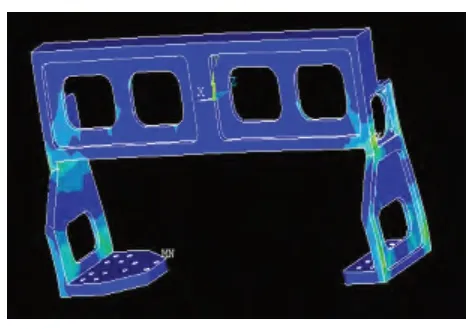
图9 优化后横梁2阶应力图

由表2可以看出，优化后1阶、2阶固有频率有所提高，说明优化后结构刚度更大，横梁在整个系统中更可靠；由图8、图9所得前两阶应力图可以看出，优化后横梁应力分布较为均匀，没有出现应力集中部位。经测试，横梁可以稳定承载桌式贴片机的整机运行，充分证实了以上分析结果。

4 结束语

通过ANSYS软件分析了桌式贴片机横梁的固有频率和振型，并在此基础上对横梁结构进行了拓扑优化，以此种分析设计方法得到了一款结构更加稳定、更加轻量化、更加契合与桌式贴片机的机械运动系统。这样不仅为贴片机的设计改进工作提供了参考，也为将来高精度仪器的设计提供了新的设计方法。

[1] 陈晔昕.电梯印板无铅焊接研究[D].上海交通大学,2007.

[2] 卢利平.载货汽车车架拓扑优化设计及有限元分析[D].合肥工业大学,2009.

[3] 胡世军,梁东旭,张代录,王瑞哲,袁铭.基于ANSYS的主轴箱体模态分析及拓扑优化[J].机械制造,2012.

[4] 德瑞西斯(德).机器动力学[M].科学出版社有限责任公司,2011.

[5] H.P. Mlejnek,R.Schirrmacher. An engineer’s approach to optimal material distribution and shape finding[J].Computer Methods Apppl, Mech Engrg.1993.

[6] Kirsch U and Topping B.H.V. Minimum Weight Design of Structural Topologies[J].J.Structural Eng.1992.

[7] Dr. Martin P. Bendsoe Optimization of structural topology[J].Shape and Material Springer-Verlag Berlin Heidelberg,1995.