四旋翼无人飞行器双闭环PID控制器设计

贺 翔，陈奕梅，郭建川，修春波

HE Xiang, CHEN Yi-mei, GUO Jian-chuan, XIU Chun-bo

（天津工业大学 电气工程与自动化，天津 300387）

0 引言

四旋翼无人飞行器因其能够垂直起降、自主悬停、可以侧飞、倒飞等高机动性能的特点，特别适用于在复杂地形与狭小空间使用，因此近年来，迅速成为UAV研究领域中的热点[1]。

四旋翼无人飞行器运动系统是由四个输入力产生六个自由度方向运动，有着非线性、多变量、欠驱动和强耦合等特点。运动系统的描述一般采用欧拉角或者四元素法[2]。针对四旋翼无人飞行器运动系统的控制和系统实现，国内外多家高校和研究机构进行了研究[3]，比较典型的控制方法有PID控制[4]，线性二次型最优调节控制（LQR）[5]，滑模变结构控制[6]，反步控制[7]和鲁棒控制[8]等，由于控制器自身的复杂性，大多数都限于仿真研究，并未能真正用于实际系统中。

针对四旋翼无人飞行器的控制方法研究，加拿大Quanser公司开发了Qball-X4实验平台，该平台由定位摄像头，四旋翼无人飞行器以及上位机组成。其中定位摄像头用来采集飞行器的位置坐标和姿态角。上位机则可以通过MATLAB编写控制算法并生成可执行程序通过Wi-Fi下载到飞行器上，并且在飞行过程中把定位摄像头采集到的飞行器位置坐标和姿态角实时传输到飞行器形成闭环[9]。

本文针对Qball-X4四旋翼飞行器，设计了一种基于双闭环PID的四旋翼无人飞行器控制方法，并将其用于实验平台，实现了室内的定点悬停飞行，该控制器由内环姿态控制器和外环位置控制器，内外环之间通过实际偏航角进行了控制量校正，提高了位移的控制精度。这种方法结构清晰，控制器参数可通过实验平台在线调节，便于工程实现。实验结果验证了控制方法的有效性。

1 动力学模型

1.1 四旋翼无人机的运动控制分析

如图1所示，Fi为第i个旋翼产生的升力，ui为第i个电机的PWM输入值，roll、pitch、yaw分别为飞行器的滚转、俯仰和偏航角。四旋翼直升机的1、3旋翼为顺时针旋转，2、4旋翼为逆时针旋转，所以当四个电机的转速相等且升力之和等于机体重力时，无人机可实现悬停，保持转速相等，升力之和增加或者减少，无人机可上升或者下降；保持升力之和等于重力，减少（增加）1、3旋翼转速，同时增加（减少）2、4旋翼转速，就会在绕z轴方向产生扭矩，无人机可实现关于y轴的偏航运动；若保持升力之和等于重力，减少（增加）1旋翼转速，同时增加（减少）3旋翼转速，无人机可实现关于x轴的俯仰运动；保持升力之和等于重力，减少（增加）2旋翼转速，同时增加（减少）4旋翼转速，无人机可实现关于y轴的滚转运动。

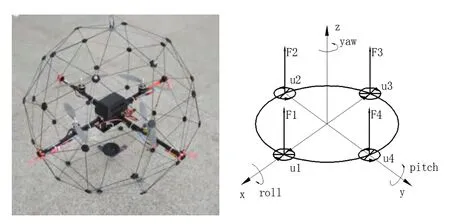
图1 Qball-X4动力学示意图

1.2 Qball-X4无人机建模

在建模过程中，假设四旋翼都能很好地与z轴平行排列且低速飞行的空气阻力为零，则可以建立无人机的动力学模型方程为[10,11]：

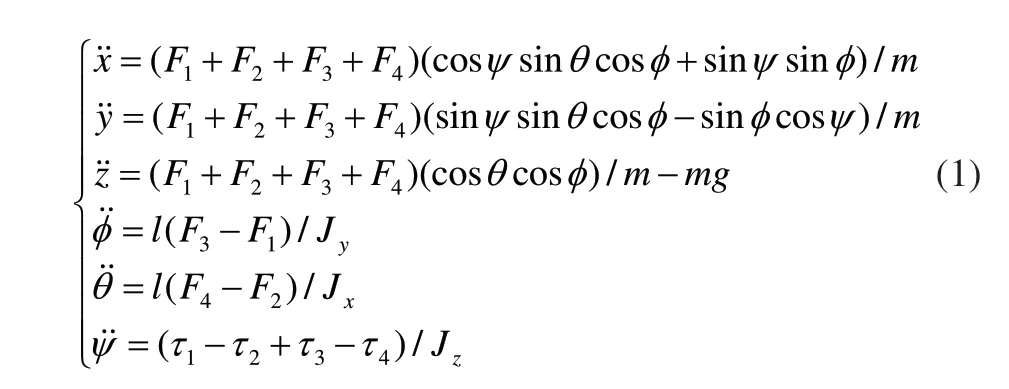
Qball-X4无人飞行器的每个旋翼产生的升力与电机的PWM输入满足一阶惯性环节，传递函数为式(2)[9]：

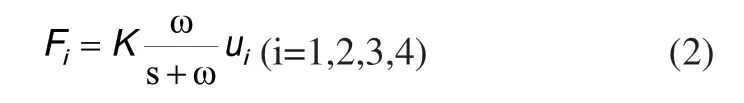
其中ui是第i个电机的PWM输入，ω是带宽，K是正向增益。

每个旋翼产生的扭矩与电机的PWM输入近似满足如下关系[9]：

把式(2)和式(3)代入式(1)中可得Qball-X4无人机动力学模型：

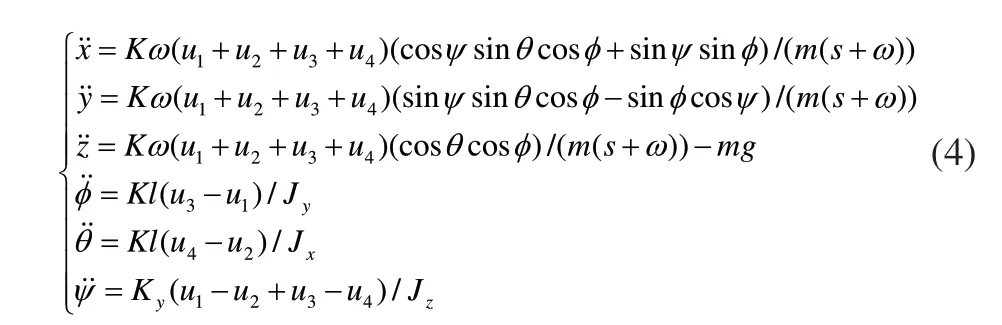
表1 Qball-X4参数表

为了便于控制器的设计，定义向量U=[U1,U2,U3,U4]T为虚拟控制量，与实际控制量即电机PWM输入为u=[u1,u2,u3,u4]T的关系为：

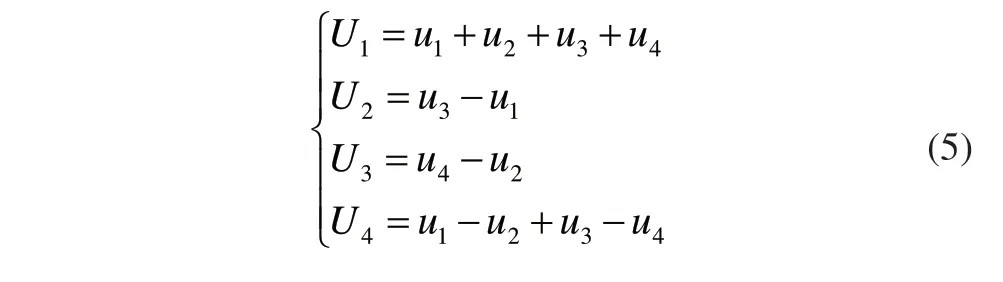
即U=A-1u，其中变换矩阵A满足：

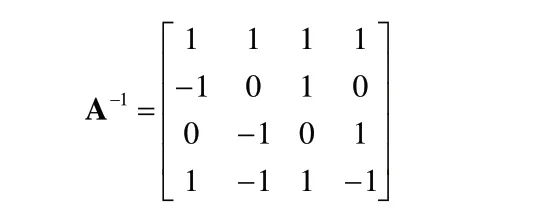
求逆可知：

则u=AU。

通过变换矩阵A-1得到Qball-X4的最终模型为式(6)：

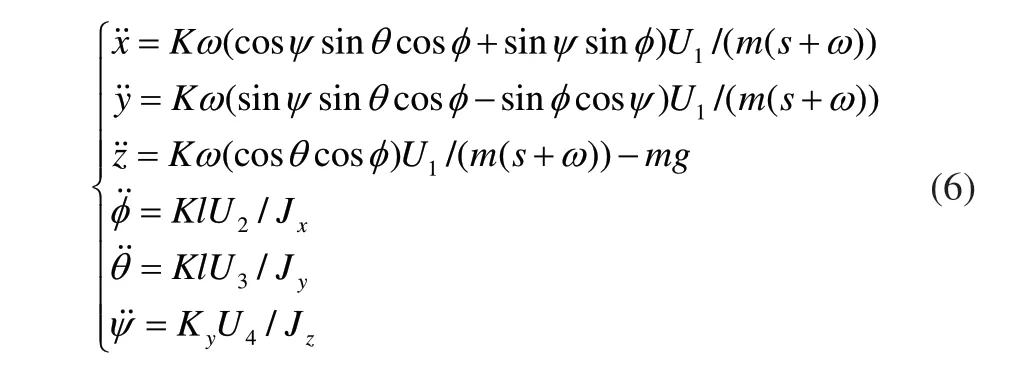
2 控制器设计

从四旋翼无人机的动力学模型可以发现，无人机的飞行过程可以分解为在机体坐标系中的姿态角变换和在惯性坐标系中的质心运动，其中惯性坐标系中的质心移动依赖于机体坐标系中的姿态角侧倾来获取侧向加速度，因此通过嵌套的内外环实现对四旋翼无人机的控制，其中内环为姿态环，外环为位置环。综合考虑方程本身的约束及定点飞行的任务目标，在设计中滚转角与仰俯角的期望值是通过位置控制系统反解得到。图1给出了控制器结构框图，其中分别是位移和偏航角的参考输入， ),,( zyx 和 ),,( ψθφ 分别是无人机位移和姿态的实际值， ),,,(4321uuuu 是四个电机的PWM输入值， ),,,(4321UUUU 是经过变换后的控制量， ),(rrΘΦ 是位移控制器的输出。

2.1 内环姿态控制器设计

根据式(6)设计姿态控制器如式(7)：

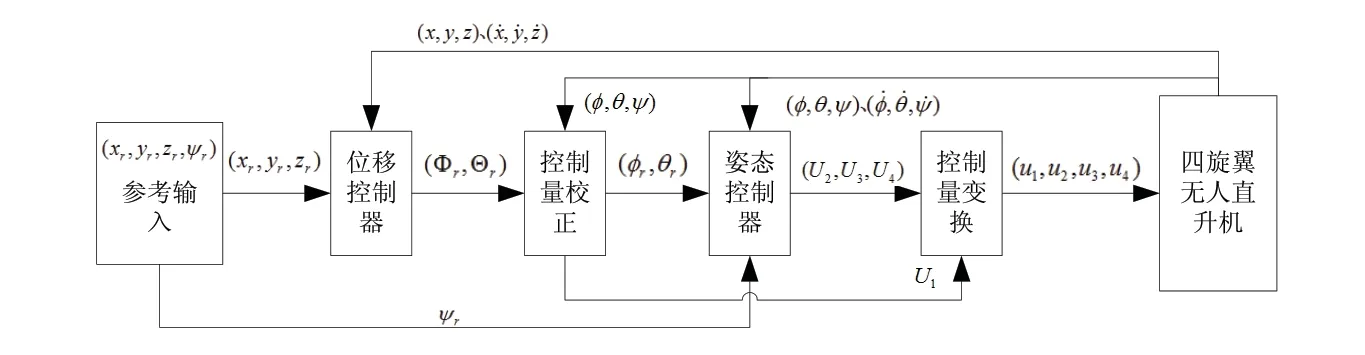
图2 控制器结构框图

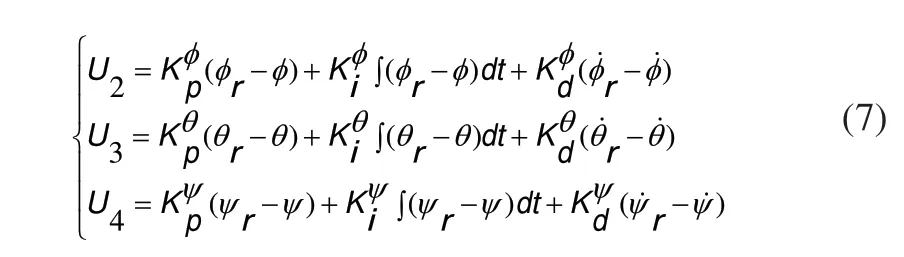
考虑到控制量可能超出电机PWM值得工作范围，故姿态角的一阶状态量期望值全部置为零。通过合理调整的值，可使飞行器的姿态角达到稳定。

2.2 控制量校正

由于外环位置控制器是在惯性坐标系下经过控制器计算得到了中间控制量，而内环姿态角则是在机体坐标系下进行闭环控制，故内外环需经过控制量较正后进行连接。

在高度z轴上满足式(8)：

其中ue为高度控制器计算输出的控制量，u是为了抵消重力所加的控制量偏置。

反解式(8)可得式(9)：

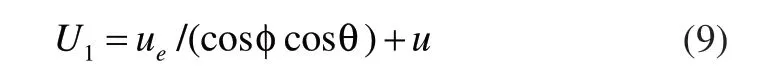
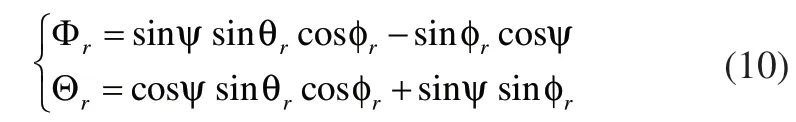
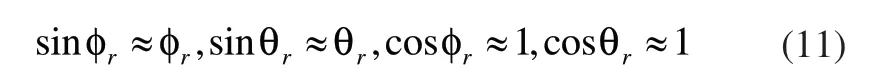
则式(10)简化为式(12)：

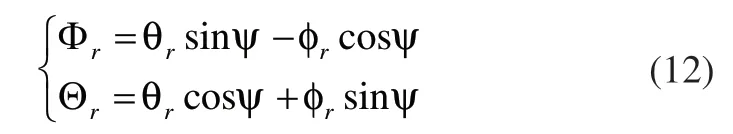
对式(12)进行反解可得式(13)：

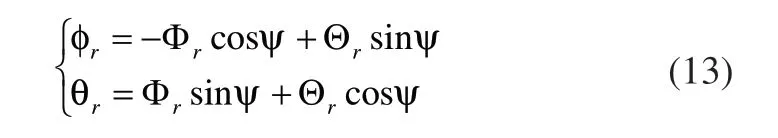
通过式(9)和式(13)进行控制量校正，连接内环姿态控制器和外环位置控制器。

2.3 位移控制器设计

本文位置控制器均采用经典PID实现控制，根据四旋翼无人机动力学模型设计如式(14)所示：

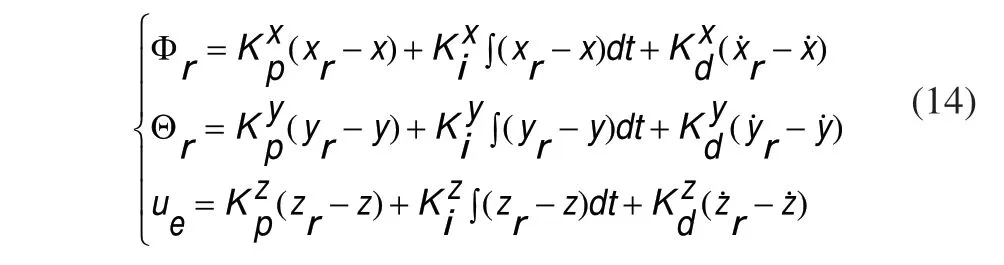
考虑控制量可能超过电机PWM值得输入范围，把位移的一阶状态量的期望值置为零。通过合理调整控制器参数可使四旋翼无人机的位移达到闭环稳定，下章将通过实验对该控制器进行验证。

3 实验验证

将上章设计的双闭环PID控制器用于Qball-X4四旋翼无人直升机，进行了定点悬停控制实验，对所设计的控制器进行了实验验证。图3是高度PID控制器的Simulink框图。

图3 高度PID控制器的Simulink框图

图3 中，高度由于存在外部重力作用，所以加入了控制量偏置，微分部分经过滤波器进行了滤波。其他位移、姿态控制器与高度控制器类似。

3.1 姿态控制器实验

由于本文采用嵌套的内外环PID实现四旋翼无人机的控制，而内环三个姿态角分别由控制量U2,U3,U4单独控制，三个通道之间完全独立，故在姿态角控制器参数调整实验过程中，可把各个通道单独调试[12]。

例 如： 若 要 调 整 滚 转 角φ ， 则 手 动 使U1=u,U3=0,U4=0（其中u为电机工作范围内的定值），而控制量U2由滚转角控制器解算，然后通过控制量变换输入到四旋翼无人机，通过观察无人机滚转角的变化，在线调整参数，使滚转角达到控制要求。另外两个姿态角也可用相同的方法进行参数整定。整定后的控制器参数如式(15)所示：

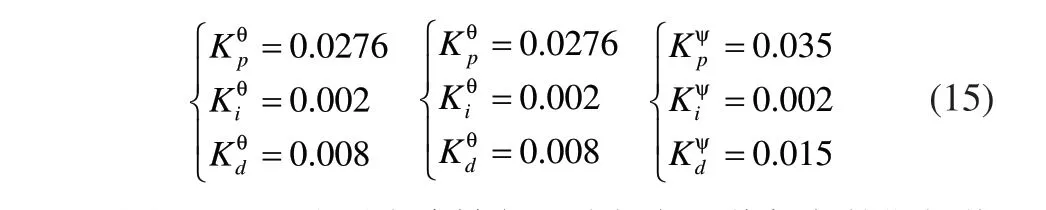
图4、5、6分别为滚转角、俯仰角和偏航角的期望值都为0°，且在初始姿态 ),,( ψθφ =(-0.18°，-15°，-6.5°时的响应曲线。由图可知，俯仰角与滚转角的稳态误差在±2°范围内，而偏航角的控制误差不超过±1.5°，取得了较好的控制效果。

图4 滚转角响应曲线

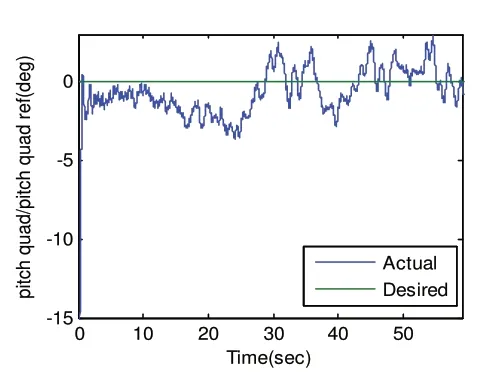
图5 俯仰角响应曲线

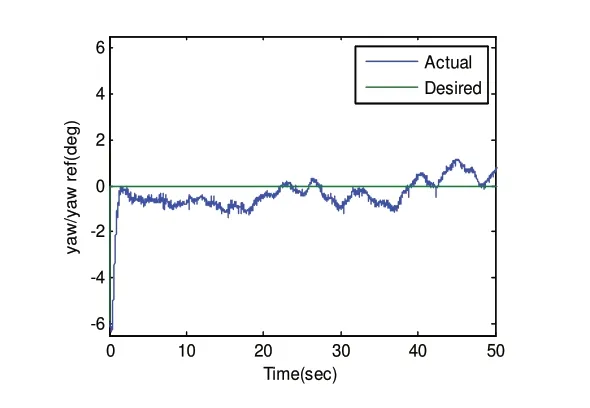
图6 偏航角响应曲线

3.2 定点悬停实验

位移控制器整定参数如式(16)所示：

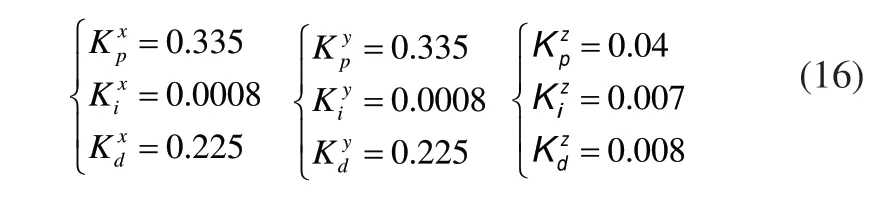
把所设计的控制器下载到飞行器上，设位置期望值为(x,y,z)=(0,0,0.5)，进行飞行器起飞和定点悬停实验，图7、图8为实验的位移和姿态角响应曲线。

由图7可知，飞行器在起飞过程中存在误差范围内的振荡，达到相对稳定后，高度(z)误差在±0.05mm的范围内，位移误差(x，y)在±0.1m的范围内小幅振荡。图8中，姿态角的跟踪误差控制在±3°之内小幅振荡。

在其他类似实验中，采用PID室内悬停的x、y轴的位移误差在±0.2m范围内[13]，比较可知，本文的控制方法是有效的，并具有较高的精度。

图9和图10是控制量的输入波形，为了保障电机的可靠运行，电机的PWM输入的额定范围应限制在[0.05,0.1][9]，本次实验的电机输入在电机的工作范围内，说明本文的控制器设计是合理的。其中，由于飞行器偏航角方向没有调平，所以虚拟控制量U在-0.01附近振荡调节，而不是在0附近。由式(5)可知，图10中控制量u2,u4高于u1,u3是符合实际情况的。

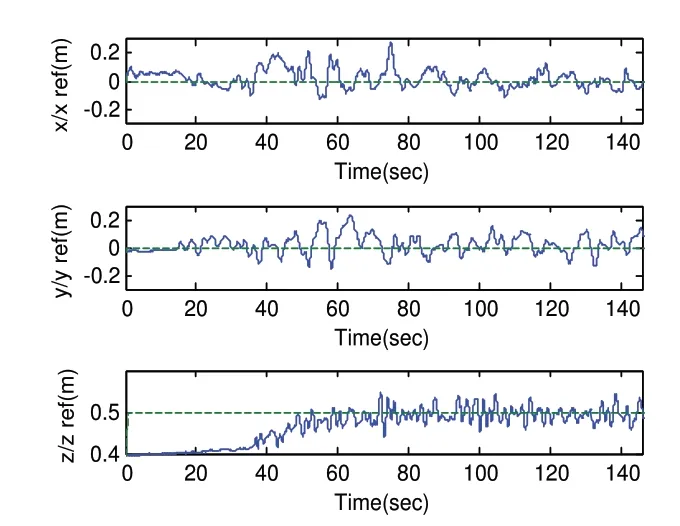
图7 位移响应曲线

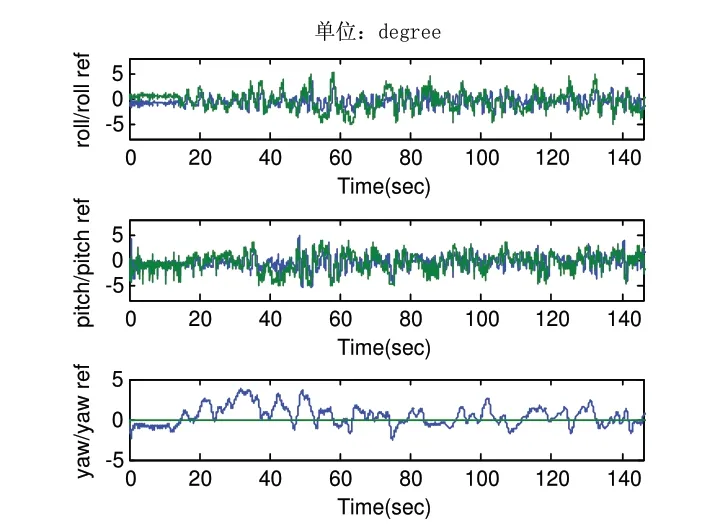
图8 姿态角响应曲线

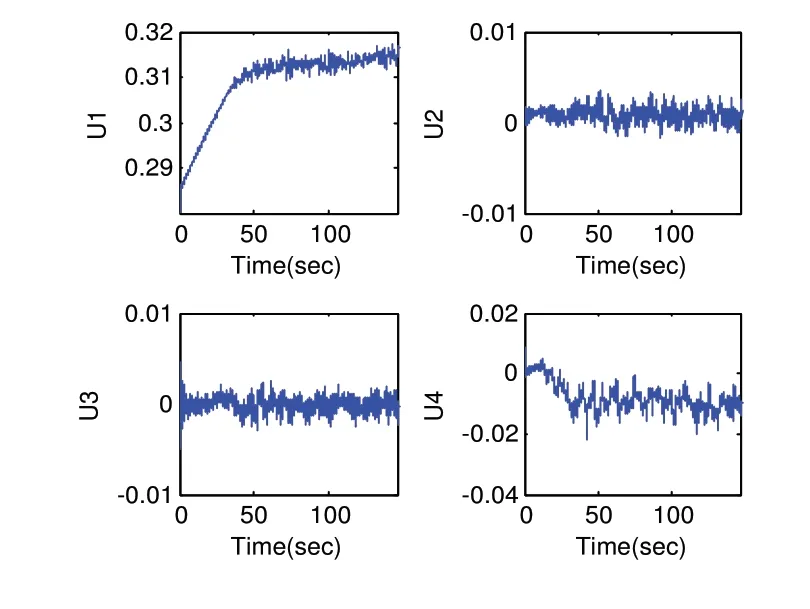
图9 虚拟控制量输入U

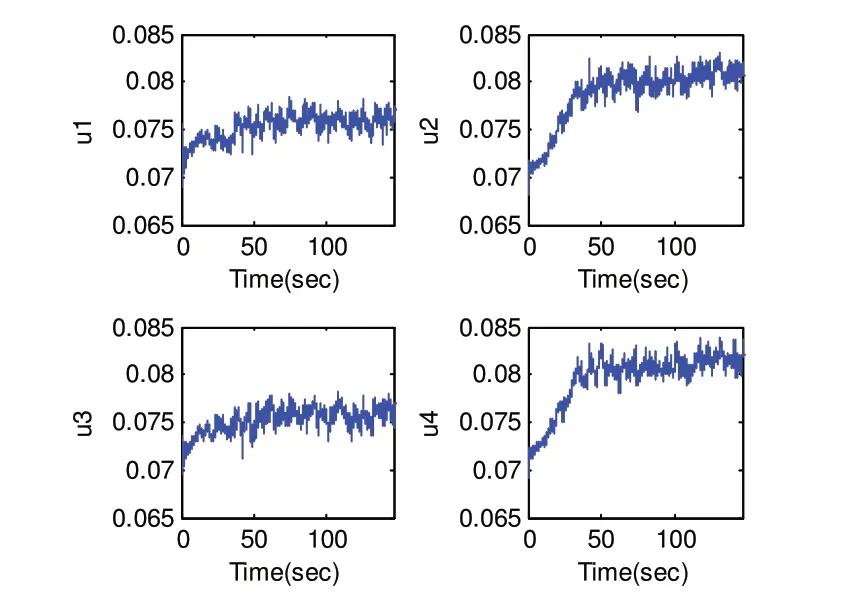
图10 电机PWM值输入u

4 结论

本文根据四旋翼飞行器动力学模型，设计了双闭环PID控制器，实现了四旋翼无人飞行器的定点悬停控制，并在Qball-X4实验平台进行了姿态控制实验和定点悬停实验，由实验结果可知，姿态角跟踪误差在±3°之内，位移(x,y轴)误差在±0.1m之内，高度控制误差在±0.05m之内，实验结果验证了控制器的有效性和精度。

在未来的工作中，将会使用该控制器结合有限状态机理论进行飞行器的自主起飞和降落以及路径跟踪方面的研究。

[1] 王璐.四旋翼无人飞行器控制技术研究[D].哈尔滨工程大学,2012.

[2] Xian Bin,Diao Chen,Zhao Bo,Zhang Yao.Nonlinear robust output feedback tracking control of a quadrotor UAV using quaternion representation[J].Nonlinear dynamics,2015,79(4):2735-2752.

[3] Zhen Zi-yang,Pu Huang-zhong,Chen Qi,Wang Xin-hua.Nonlinear intelligent flight control for quadrotor unmanned helicopter[J].Transactions of Nanjing University of Aeronautics and Astronautics,2015,01:29-34.

[4] Wahyudie A.,Susilo,T.,Noura, H. Robust.PID Controller for Quadrotors[J].Journal of Unmanned System Technology,2013,1(1):14-19.

[5] 高青,袁亮,吴金强.基于新型LQR的四旋翼无人机姿态控制[J].制造业自动化,2014, 36(10):13-16.

[6] Mohd Basri,Mohd Ariffanan,Husain,Abdul Rashid,Danapalasingam, Kumeresan A.Intelligent adaptive backstepping control for MIMO uncertain non-linear quadrotor helicopter systems[J].Transactions of the Institute of Measurement and Control,2015,37(3):345-361.

[7] Zheng En-Hui,Xiong Jing-Jing,Luo Ji-Liang.Second order sliding mode control for a quadrotor UAV[J].ISA Transactions,2014,53(4):1350-1356.

[8] 甄红涛,齐晓慧,夏明旗,苏立军.四旋翼无人机鲁棒自适应姿态控制[J].控制工程,2013,20(5):915-919.

[9] Lucia,W.,Sznaier,M.,Franze,G. An obstacle avoidance and motion planning CommandGovernor based scheme: The Qball-X4quadrotor case of study[C].2014 IEEE 53rd Annual Conference on Decision and Control,2014:6135-6140.

[10] 谭广超.四旋翼飞行器姿态控制系统的设计与实现[D].大连理工大学,2013.

[11] WANG Hong-yu,ZHAO Jian-kang,YU Wen-xian,TIAN Wei-feng. Modelling and position tracking control for quadrotor vehicle[J]. Journal of Chinese Inertial Technology,2012,20(4):455-458.

[12] 郭建川,鲜斌,王福,张旭.三自由度无人直升机实验平台与飞行姿态控制器设计[A].第三十二届中国控制会议[C].2013:733-738.

[13] 白永强,刘昊,石宗英,钟宜生.四旋翼无人直升机鲁棒飞行控制[J].机器人,2012,34(5):519-524.