三步法工业机器人矢量坐标变换

郑相周，董旺远

ZHENG Xiang-zhou1, DONG Wang-yuan2

（1.华中农业大学 工学院，武汉 430072；2.华中农业大学 理学院，武汉 430072）

0 引言

矢量坐标变换是多体系统运动学和动力学分析的基础[1]。工业机器人是典型的多体系统，矢量坐标变换是工业机器人运动学分析的首要环节[1～3]。

工业机器人具有树形拓扑结构，几何特征鲜明。1955年Denavit和Hartenberg提出了工业机器人矢量变换的系统方法[2]（简称D-H方法）。

D-H方法使用齐次矩阵刻画相邻连杆间的位姿关系。齐次矩阵的4个关节参数由3个结构参数和1个关节变量组成。D-H方法对连杆坐标系的设置和关节参数做了严格定义，使得D-H方法具备了系统理论的特点，便于计算机建模[2]。虽然工业机器人关节大多为单自由度，但结构仍比较复杂。在人工进行分析时，D-H中坐标系和关节参数的严格定义使得D-H方法难以应用，坐标系、关节参数和关节变量范围均难以确定，一旦发生错误，分析结果将南辕北辙。

为克服D-H使用中的困难，本文提出工业机器人矢量变换三步法，相邻连杆齐次变换矩阵由方向余弦矩阵和典型的转动矩阵或移动矩阵构成。这种方法步骤简单，结构参数和关节变量区分明确，关节变量范围易于确定，适于单自由度关节的工业机器人运动学建模与分析。

1 典型齐次变换矩阵

刚体任何运动可视作移动和转动的叠加，刚体位姿由与刚体固连的连体系描述。刚体运动可分解为连体系{I}在参考系{O}中的移动和转动。在典型情况下，描述连体系方向的齐次变换矩阵具有简单形式。连体系{I}绕{O}中z轴转动的齐次矩阵[2]（称为转动矩阵）为：

式中 (,)··Rot 的2个参数分别为坐标轴单位矢量和旋转角度，其中称为旋转矩阵。

连体系{I}沿{O}中矢量r移动的齐次矩阵[2]（称为移动矩阵）为：

其中，E为3×3单位矩阵。

D-H方法将相邻连杆位姿关系分解为两个移动和两个转动，其变换矩阵是式(1)～式(2)的矩阵组合结果。

2 坐标变换三步法

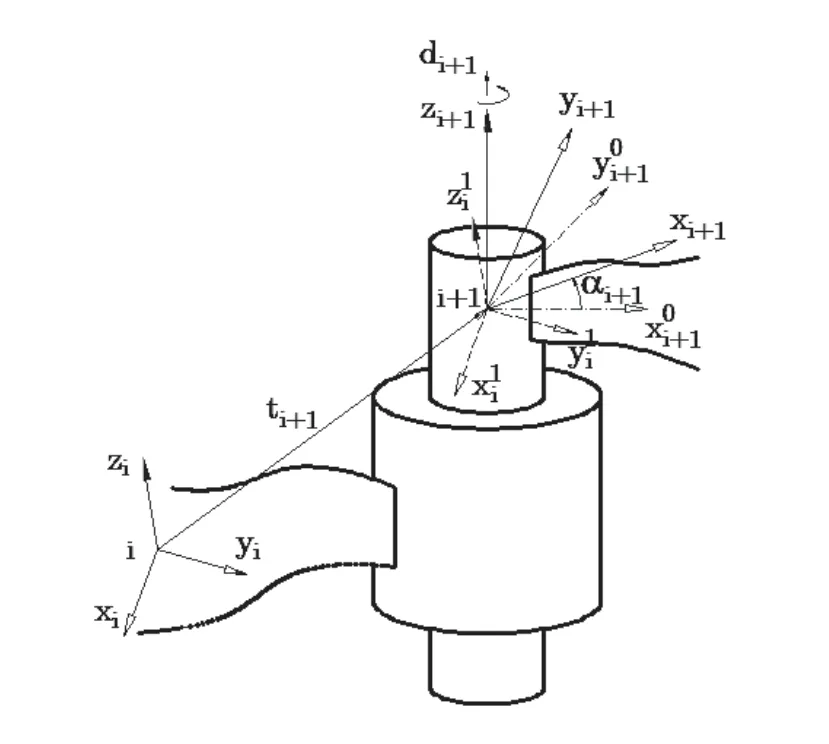
图1 三步法坐标变换原理

{i + 10}到{i1}的转动矩阵使用方向余弦矩阵描述：

上式中，∗·∗为两个沿坐标轴的单位矢量的点积。

分析上述3个变换步骤可知，前两步描述相邻连杆的结构参数，第3步描述后一个连杆相对前一个连杆的运动。

相邻连杆坐标变换式(8)中仅有由式(6)，式(7)表示的变换矩阵描述连杆运动，因此，控制连杆运动的关节变量或就与结构参数明显区分开来。

在工业机器人中，后一个连杆总是相对前一个连杆运动，在设置连体系时，就可以直接将运动前的连体系视作运动后的连体系，这样对分析结果没有影响，不仅可简化连体系设置，还可以将作为运动基准，可以很容易地以此确定关节变量变化范围。这样式(5)可进一步使用楔积符号记作：

这样，使用3步法进行坐标变换，形式上相邻连杆的坐标系只需要连体系和

3 实例分析

如图2所示为5自由度机械手的前4个关节设计示意，4个关节均采用转动副，坐标系设置如图2所示，其中{0}为机座坐标系，其他为连杆连体系。除右手直角坐标系的z轴取转动副轴线外，其他坐标轴方向根据结构特点确定，无须遵守其他规定。

以连杆1、2为例说明3步法坐标变换使用：

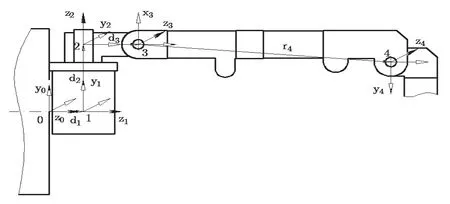
图2 机械手坐标系设置

连杆2到1的齐次变换矩阵即为这3个齐次矩阵的乘积。

图2所示相邻连杆坐标变换如表1所示。

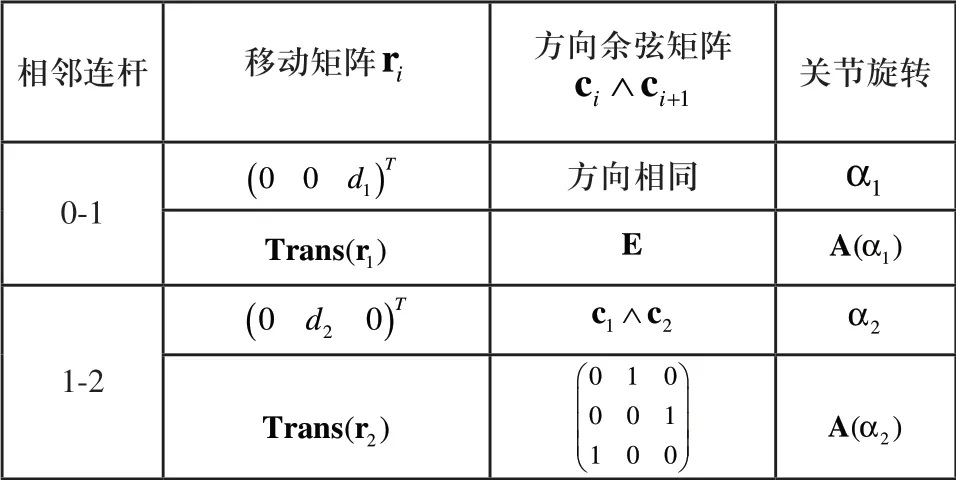
表1 相邻连杆坐标变换

表1 （续）

4 结论

本文提出的工业机器人3步法坐标变换方法，使用描述结构参数的移动矩阵、方向余弦矩阵和描述关节运动的旋转矩阵（转动副）或移动矩阵（移动副）组合来获得相邻连杆间的矢量齐次变换矩阵，概念清晰，相关参数意义明确，避免了使用D-H方法需要严格按照定义进行坐标系设置和关节参数确定的弊端，适合单自由度关节的工业机器人运动学人工建模分析。

[1] J. J Craig.Introduction to Robotics(3Ed)[M].London, UK:Prentice Hall,2003.

[2] 郑相周,唐国元.机械系统虚拟样机技术[M].北京:高等教育出版社,2010.

[3] Siciliano,L.Sciavicco, L.Villani, G. Oriolo. Robotics,Modelling, Planning and Control[J].London,UK:Springer-Verlag,2009.