基于vissim的车队离散特性研究

孙玮玮，李 康，郝斌斌

（兰州交通大学 交通运输学院，甘肃 兰州730070）

随着社会经济的快速发展，我国各大城市交通路网逐年扩大，机动车保有量持续增加，居民出行次数也在增加，城市交通拥堵现象在各个城市中呈现蔓延趋势。在城市的主干道，商业集聚地段，信号灯设置较多地段及交通构成较复杂地段，进出城的通勤走廊路段极易发生交通拥堵现象，有时单个交叉口的拥堵又会造成临近交叉口的拥堵。同时交通拥堵现象的发生具有规律性，大部分集中在以下几个时间段:周内的早晚高峰期，周末或其他节假日，大型活动期间等。交叉口间的车流运行状况直接影响了相邻交叉口的信号配时设计方案，车队行驶离散特性的探究关系着交通拥堵的缓解状况。

因此，本文以车队行驶离散特性研究为基础，重点研究车队离散特性与路段长度以及车流分布的关系。对影响车队离散特性的因素进行总结和分析，能够在一定程度上缓解交通拥堵，在车辆行驶过程中，减少停车次数，降低延误，对于提高整个交通路网的运行效率，提供一定的理论依据。

1 研究现状

1.1 国外研究现状

G.M.Pacey提出派西方法（Pacey），假定车队在离开停车线驶向下游停车线的过程中，车速是恒定不变的，但是整个车队中各个车辆的速度是不同的，而且每一种车速出现的频率是服从一种经过变换的正态分布的。D.I.Robertson提出分析车辆离散程度的另一种方法——几何分布函数。他指出车流中各车辆，在一对固定起讫断面之间的实际行程时间是各不相同的，并且它们按照一种确定的几何函数规律分布。P.A.Seddon曾经利用现场实际观测的数据，对以上两种方法做对比验证，发现二者都很接近实际观测结果。A.F.Rumsey和M.G.Hartley对派西和罗伯逊提出的两种分布函数进行计算机模拟对比试验，发现根据两种不同的分布函数推算出的下游交叉口车流到达率虽然有差别，但对于下游交叉口的信号配时设计影响不大。

1.2 国内研究现状

杨佩昆等人在基于对城市道路上车流运行机理进行微观分析的基础上，提出自由流随机度的概念，并建立适用于城市道路车队离散过程中的交通流模型，使交通流理论的有关参数取值精度得到较好改进，段源华等人通过分析我国混合交通状况下交通流特性，建立在交通控制系统中车队离散规律动态模型。同时对车队离散模型进行复域变换，同时对车队离散动态系统进行稳定性分析与实际运算，使得该模型更符合我国实际道路交通状况。刘灿齐等人运用流体动力学模拟理论对车队在信号灯交叉口排队队长的变化特性进行微观分析，建立密度散布模型，并将该模型用来推导离散车队尾部在下游信号灯被拦截车辆数量的数学表达式，为交叉口信号协调控制提供依据。王殿海等人在长春市交通调查数据的基础上分析并验证经典车队模型。对经典车队模型进行改进，从而建立拥有良好预测效果的基于无变换正态分布的车队离散模型。同时提出交通流量反馈机制预测方法，提高流量预测精度，对城市交通控制有重要理论意义和实用价值。张萌萌等人通过改进开放性边界条件，利用以为元胞自动机模型模拟协调控制主干道交通流状况，采用差分方程的形式描述车辆动态行为。

2 经典车队离散模型及其影响因素

2.1 正态函数分布

Pacey方法是G.M.Pacey在上世纪50年代中期提出的，该方法做了如下假设:车辆离开上游交叉口，从上游交叉口的停车线位置开始，在进入下游交叉口的行驶过程中，速度保持不变。但是在所有车队当中，每一辆车的行驶速度，并非完全相同，每一种行驶速度的出现频率，分布是服从一种固定的规律分布，Pacey方法中这种分布规律为经过变换的正态分布。按照他的理论，第j个时间段内，下游断面车流的到达率情况，可以推算出式（1）

式中:qd（j）为第j时段下游某断面上的车流到达率（veh／h）；qo（i）为第i时段上游停车线断面的车流通过率（veh／h）；g（j－i）为从上游停车线断面开始，到下游某断面之间的路段上车辆概率分布函数。

按照G.M.Pacey的离散理论，车辆在路段上行驶，车辆行驶时间的概率分布，服从一种变换的正态分布函数，如式（2）

式中:T为车辆行驶的时间；a为上游停车线到下游某断面之间的距离；为车队的平均行驶速度；S为车流中不同车辆所具有的行驶速度的标准差。

2.2 几何分布函数

罗伯逊在上世纪70年代初期，提出的几何分布函数，是另一种分析车辆离散特性的方法。按照该方法，在上游停车线到下游某一断面上，车辆的通过率有如下的数学关系，如式（3）

式中:qd（i＋t）为下游某断面上，在第（i＋t）时段预计的车辆达到率；qo（i）为上游停车线断面上，在第i时段车辆通过率；t为上游到下游两个断面之间，车辆平均行驶时间的0.8倍；F为是一个大小系数，表示的是车流在运动过程中的离散程度，称作车流离散系数。

上文所述的车流离散系数F，表征的是车流中每辆车行驶速度的差异。也就是说，车流当中，不同的车辆，在固定的起讫断面之间，实际行驶的时间是不一样的，它们都服从某一种固定的分布规律。从文中式（3）可以看出:车流当中车辆的行驶时间，是服从几何函数分布的，也就是说将式（3）作相应的改写，便可以得出这一分布规律:

令j＝i＋t，则i＝j－t

于是有

得

同样

得

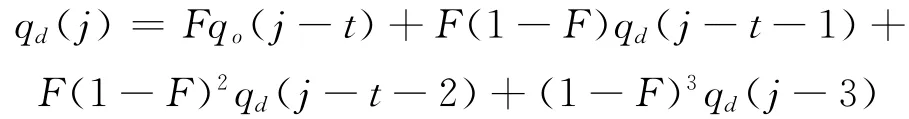
以此类推便有

因为qo（0）＝0，所以可得

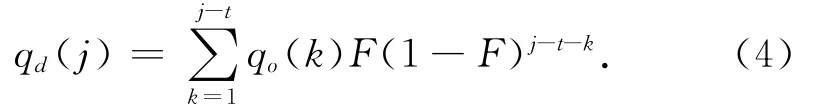
式（4）的形式与统计学中指数平滑法公式是一致的，即下游断面的流量值是由上游断面的过去时间流量值的加权平均得到的，最近时间（j－t）时的流量值的权数F最大，（j－t－1）时间的流量值的权数F（1－F）次之，（j－t－2）时间的流量值的权数F（1－F）2更次之，以此类推，愈远的流量值，其权数愈小。

2.3 离散系数F确定

从当前的情况看，罗伯逊提出的基于几何分布假定，建立的经验式（4）应用较为广泛，被世界上许多国家广泛应用的信号协调配时设计程序——TRANSYT就使用这一公式来推算下游停车线断面上“流量－时间”图示。在该公式中，至关重要的一步是离散系数F值的确定。

罗伯逊根据实地观测数据和经验，得出如下式计算F值

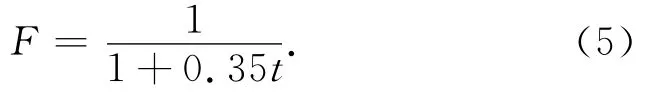
式（5）已经被西方国家的许多学者验证，认为基本上与实际观测数据吻合。

2.4 车队离散规律影响因素

现阶段由于我国城市道路的复杂情况，有很多影响车队离散规律的因素。路段上的平均行程时间、交通流的饱和度、交通流的构成、交通流受干扰程度等都影响着车队离散规律。

1）一般说来，越长的路段其车流的平均行程时间就越长，车队离散程度高。反之，车队离散程度低；

2）交通流饱和程度越高，则其中的车辆行驶自由度就越小，车队离散程度就越低。反之，车队离散程度越高；

3）由于交通流的构成很复杂，车辆性能存在很大的差异，导致在车辆的行驶速度上，也有很大的差异，车队离散程度也就越高；

4）由于行人、自行车等干扰因素的存在，对于车辆的行驶速度来说，容易受到干扰。由于强烈的干扰，致使车辆行驶速度很缓慢，从而车队的离散程度就很低。而且干扰因素的位置，对车队离散性也存在影响:假如干扰发生在车队头部位置，则增加整个车队平均行程时间；假如干扰发生在车队中部位置，则可能将车队分隔开成为两个或多个车队。

3 vissim仿真与结果分析

3.1 vissim仿真

本文利用vissim仿真软件对兰州市安宁区建宁东路上的四个交叉口进行仿真，路段的编号以及交叉口的编号如图1所示。

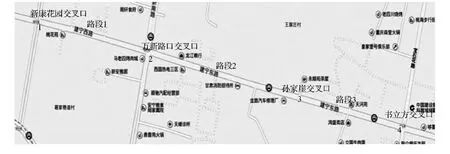
图1 兰州市安宁区建宁东路示意图

调查得到各交叉口间距如表1所示，各交叉口交通基础数据如表2所示，干道协调控制后的信号配时参数如表3所示。

表1 交叉口间距调查结果 m

表2 各交叉口交通基础数据

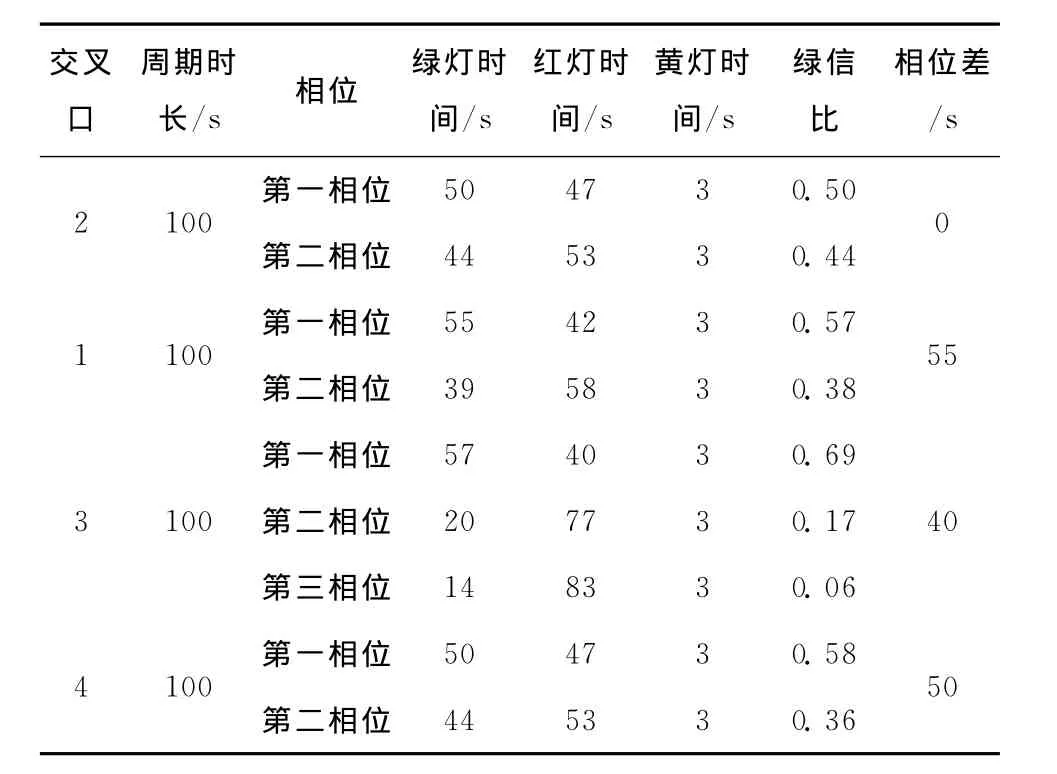
表3 协调控制信号配时参数

利用vissim软件仿真时，在路段2上，距离2号交叉口500m断面处设置检测器。首先在默认情况下对断面处的车辆到达进行检测，其次改变车流分布，然后再次对该断面处车辆的到达进行检测，得到车流分布变化后车队离散数据。最后在不改变车流分布的条件下，改变路段2的长度，当路段2的长度增加100m时，再次对该断面处车辆的到达进行检测，得到路段长度变化后车队离散数据。检测时以5s为一时段，检测周期为200s。

1）采集路段2上d＝500m处进行2个周期的断面流量，断面流量数据如表4所示；

2）改变路段2的长度，采集路段2上d＝500m处进行2个周期的断面流量，断面流量数据如表5所示。

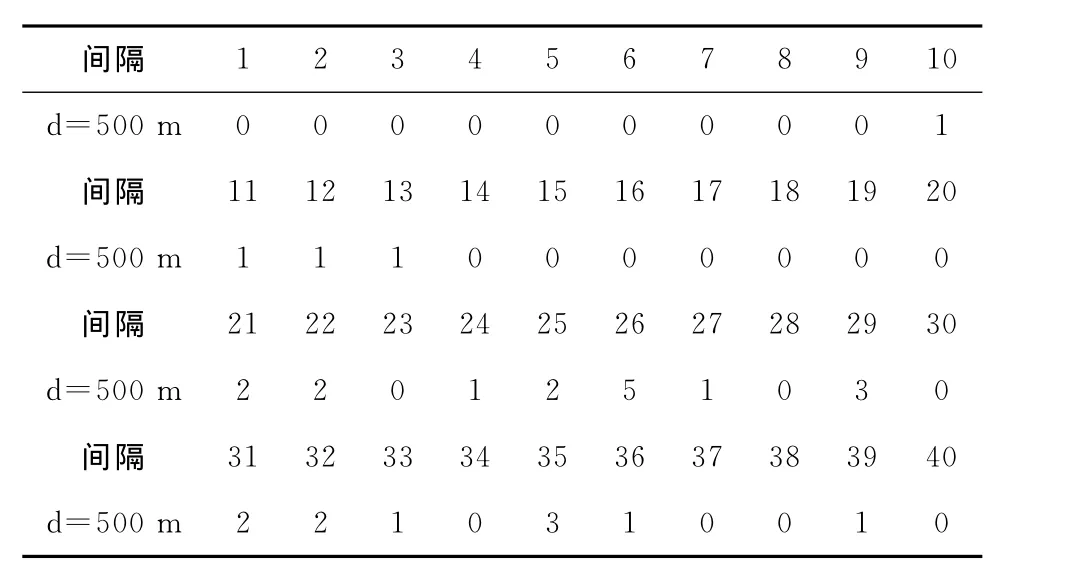
表4 路段2断面流量 （veh／5秒）

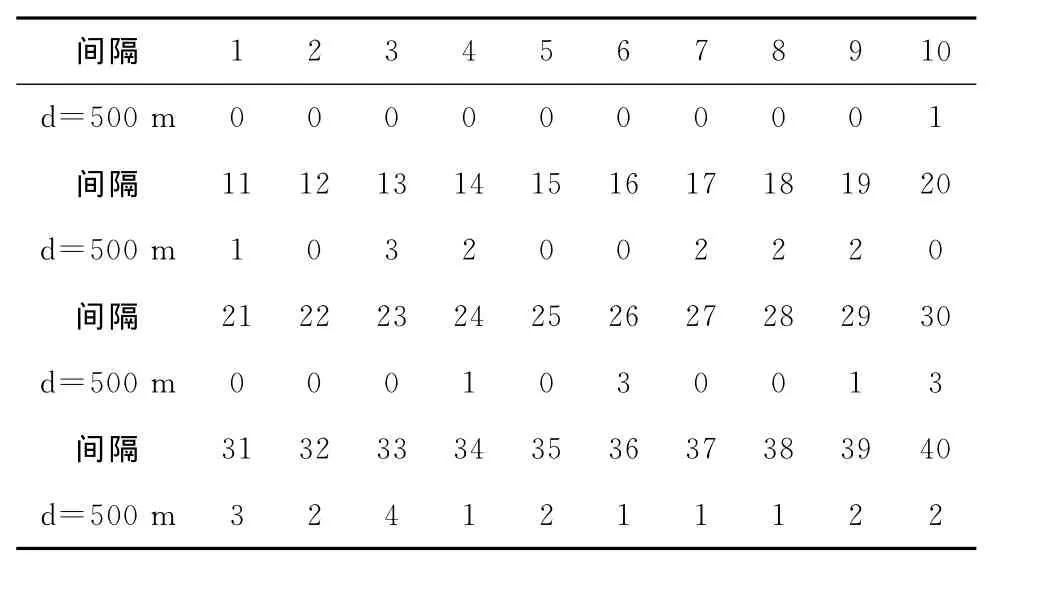
表5 延长路段2的长度后断面流量 （veh／5秒）

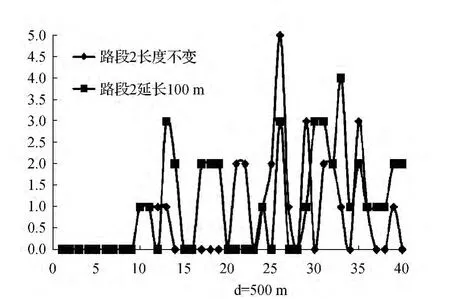
图2 断面流量对比

3.2 结果分析

如图2所示，图中曲线分别以距离路段起点500m处断面流量图示。横轴表示时间段，每一个时间段为5s，共有40个时间段，共200s即2个周期的时间。纵轴为通过该断面的车辆数。其中蓝色曲线为路段2长度不变时的检测数据，红色曲线为路段长度2增加100m时的检测数据。利用C＋＋编程，可以0.01为单位通过遍历a所可能的值，最终找到能够比较准确描述该路段车队离散特性的a值，通过反复进行模拟计算发现，当a取值为0.15时，计算所得数据与检测数据结果比较吻合。增加路段2的长度之后，用同样的方法，通过反复进行模拟计算发现，当a取值为0.17时，计算所得数据与检测数据结果比较吻合。由此可以看出，随着路段长度增加，车队离散系数参数值变大，即车队离散特性增强。

4 结束语

本文对车队离散特性与车流分布以及路段长度之间的关系进行了相应的研究，通过对实际路段上某一断面车辆到达情况进行分析，当路段长度延长后，路段上车队离散系数参数值变大，车队离散特性增强。

［1］ Pacey G M.The progress of a bunch of vehicles re－leased from a traffic signal［J］.Road Research Laboratory Note RN／2665／GMP，1956.

［2］ Robertson D I.TRANSYT:a traffic network study tool［J］.1969.

［3］ 杨佩昆，黄文忠，车丕明.城市道路车队离散过程中的交通流模型［J］.同济大学学报，1994，22（3）:294－299.

［4］ 段源华，原振友，李元城.车队离散实用动态模型及其复域变换特性研究［J］.哈尔滨建筑大学学报，1995，28（2）:97－101.

［5］ 刘灿齐，杨佩昆.车队密度散布模型及在车队截尾问题上的应用［J］.中国公路学报，2001，14（1）:89－91.

［6］ 王殿海，李凤，宋现敏.一种新的车队离散模型及其应用［J］.吉林大学学报，2009，39（4）:891－895.

［7］ 张萌萌，贾磊.城市协调控制主干路交通流模型［J］.控制理论与应用，2011，28（11）:1679－1684.

［8］ 王福景，于继承，赵雨旸，等.基于VISSIM仿真的生态驾驶行为对交叉口运行效率影响［J］.交通科技与经济，2014，16（2）:109－113.