城市轨道交通岛式站台纵列式停车线长度设计研究

王海鑫

(广州地铁设计研究院股份有限公司，510010，广州∥工程师)

城市轨道交通运营列车发生故障后，需及时离开正线，以确保其他列车正常运行。停车线可保证故障列车就近临时停放，避免对正线运行的干扰。当故障列车距离车辆基地较远时，停车线的合理设计尤为重要。GB 50157—2013《地铁设计规范》规定，正线应每隔5～6座车站或8～10 km设置停车线，其间每相隔2～3座车站或3～5 km应加设渡线[1]。加设停车线后，车站工程量增大，特别是地下线路，其工程难度和造价都将大大增加。因此，在满足规范及停车功能的情况下尽量减小停车线规模，就成为设计的关键。

1 停车线分类

按与车站有效站台的位置关系，停车线可分为纵列式和横列式。

1)纵列式停车线设置在车站的一端，与站台纵列，能将乘客上下车与车辆技术作业的位置分开，有利于列车临时停放与车辆检查[2]。但纵列式停车线会使车站范围加长，且对线路线型条件有一定要求。若不得已设置于曲线段，则设计为贯通式停车线的难度较大。纵列式停车线通常设置于运营交路的起终点，与折返线结合布置。

2)横列式停车线设置在车站的一侧，与站台平行。该布置相对紧凑，在紧急情况下故障列车可到达停车线后再清客，以减少占用正线时间[2]。但横列式停车线会使车站范围加宽：如为高架车站，则增加施工难度；如为明挖施工的地下车站，则对道路交通影响较大，造成交通疏解困难。此外，横列式停车线还会造成站台分离，使上下行方向站台不能直接连通，不便客流组织。横列式停车线通常设置于非折返站，或纵列式停车线难以实施的车站。

由于横列式停车线和侧式站台纵列式停车线在确定具体配线形式后，包括停车线长度在内的线路设计方案较为明确，因此本文仅对应用最广泛的岛式站台纵列式停车线进行研究。

2 停车线长度

在实际工程设计中，因停车线与停车线之间间距不同，停车线与正线之间的间距也不同，故停车线长度存在差异。岛式站台纵列式停车线是最常用的停车线布置方式。本文以此类停车线为例，研究贯通式停车线影响因素并计算停车线长度。

2.1 双停车线方案

纵列式停车线适用道岔前端计算方式，其有效站台端部至岔心的距离仅与采用的道岔型号有关。GB 50157—2013《地铁设计规范》规定，车站端部渡线宜采用9#道岔。当采用9#道岔时，其道岔前端，道岔中心至有效站台端部距离不宜小于22.0 m，其道岔后端，道岔警冲标或出站信号机至有效站台端部的距离不应小于5.0 m[1]。

在停车线末端，车站端墙位置同车挡尺寸及连接正线道岔的位置有关。考虑车挡安装及维修空间，端墙与车挡的距离宜大于2.0 m。根据《地铁设计规范》规定，贯通式停车线有效长度(不含车挡长度)不应小于远期列车长度+60.0 m[1](包括50.0 m安全距离和10.0 m信号设计长度[3])。车挡前单渡线岔心距离车挡前端长度与道岔号数有关。正线一般采用道岔不小于9#，相应的车挡前单渡线岔心与端墙距离不宜小于53.0 m。根据《广州市轨道交通新线工程设计技术标准》，当采用9#道岔时，站端道岔岔心与盾构管片起点距离不宜小于16.0 m[4]。停车线与正线线间距按可设置单渡线的最小线间距4.2 m计算[1]，则与停车线相连的单渡线岔心距离端墙不宜小于53.8 m，如图1所示。由此可知，车站末端端墙的设置主要受停车线尾端道岔位置控制。

尺寸单位:m

确定道岔型号，就能确定有效站台端部至停车线前端道岔岔心的距离；确定停车线尾端道岔位置，就能确定车站端墙的位置。因此，停车线长度计算需考虑有效站台的近端岔心至远端岔心的距离。如图2所示，纵列式双停车线长度L为：

图2 纵列式双停车线示意图

L=L1+2L2+L3+L4

(1)

式中：

L1——按远期规划的列车长度；

L2——道岔前长、信号机与基本轨缝距离及司机瞭望距离之和；

L3——有效站台的近端渡线水平长度；

L4——有效站台的远端渡线水平长度;

α——辙叉角；

s——正线线间距；

d1——停车线线间距。

其中，L1由远期规划的车辆选型及列车模块确定，L2与道岔选型及信号设计有关，L3和L4同道岔选型及线间距有关，则：

(2)

L=L1+2L2+scotα

(3)

当车辆选型确定时，L与d1无关。s越大，则L越长；道岔型号越大，则L越长。

根据信号设计要求，计轴器与岔尖前基本轨缝的距离一般为1.2 m，司机瞭望距离一般为5.0 m，停车误差一般为2.0 m，实际工程中的L2应根据具体城市及具体实施条件确定。根据《广州市轨道交通新线工程设计技术标准》，当采用9#道岔时，L2取24.0 m；当采用12#道岔时，L2取值为26.0 m[4]。如选用8辆编组A型车、9#道岔，则L1=186.0 m，L2=24.0 m，cotα=9，则L=9s+234.0 m。图3为双停车线方案中L-s的关系曲线。

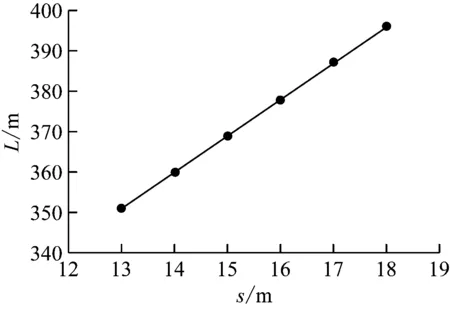
图3 双停车线方案中的L-s关系曲线

2.2 4条渡线单停车线方案

由于工程条件限制，在双停车线实施难度较大的情况下，可采用单停车线设计，并在4个方向设置4条渡线与正线互通(见图4)，以便列车进出。

图4中的停车线长度L为：

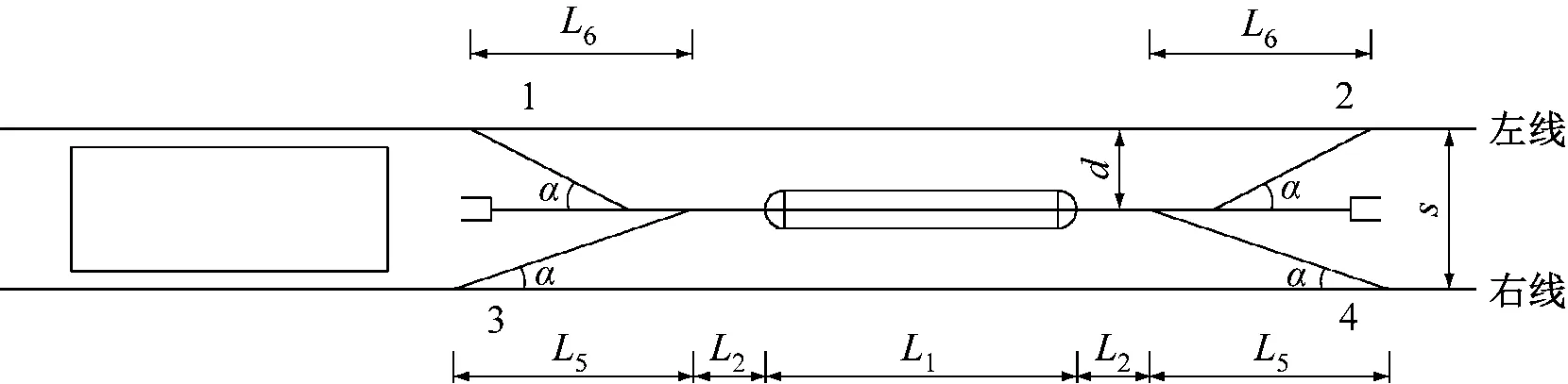
注:d——停车线至左线间距。

L=L1+2L2+2max(L5,L6)

(4)

式中：

L5——渡线3的水平长度；

L6——渡线1在左线岔心至渡线3在停车线岔心的水平距离。

L5和L6与道岔选型及线间距有关，若道岔前长为a、道岔后长为b，则：

L5=(s-d)cotα

(5)

根据《地铁设计规范》，配线中两组道岔顺向布置时插入钢轨长度la=6 m。一般情况下轨缝距离为lb=8 mm，则：

L6=dcotα+a+b+la+lb

(6)

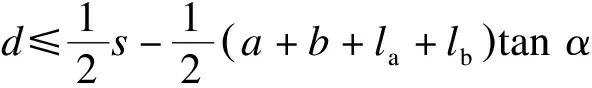
L=L1+2L2+2L5=

L1+2L2+2(s-d2)cotα

(7)

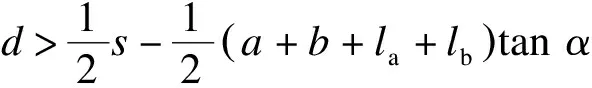
L=L1+2L2+2L6=

L1+2L2+2dcotα+2(la+lb)+2a+2b

(8)

在8辆编组A型车、9#道岔的条件下，L1=186.0 m，L2=24.0 m，cotα=9，a=13.84 m，b=15.73 m，代入式(7)和式(8)计算可知：当d≤0.5s-1.98 m时，有L=18s-18d+234.0 m；当d> 0.5s-1.98 m时，有L=18d+305.15 m。若按一般车站有效站台宽度为11.0 m，则s为固定值(14.2 m)时，L-d关系曲线如图5所示。

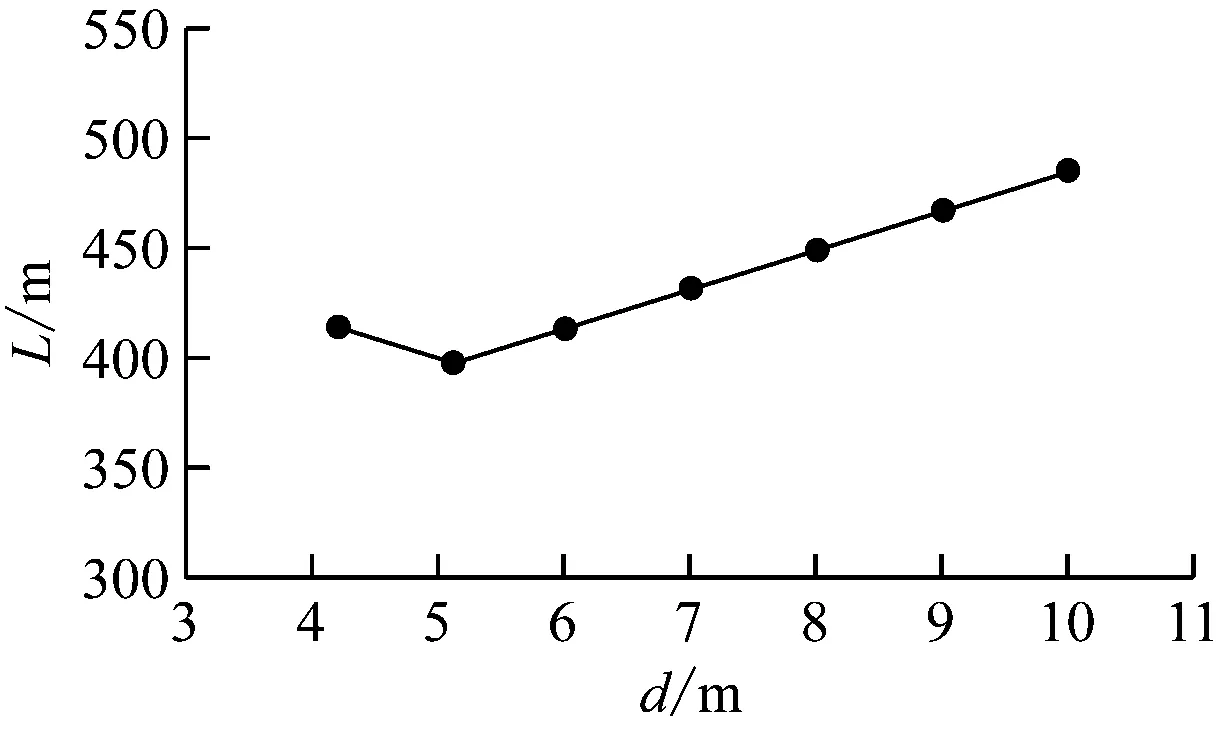
图5 4条渡线单停车线的L-d关系曲线

由图5，在s=14.2 m的情况下，当d=5.1 m时，L最小，4条渡线单停车线方案设计最优。

2.3 3条渡线单停车线方案

从工程实施影响及造价等方面考虑，3条渡线单停车线方案也较广泛地应用在实际中。相对4条渡线单停车线，3条渡线单停车线方案减少了1条渡线，可适当减小车站规模，节省土建投资[5]。

渡线的设置需考虑行车方向及故障车推送需求。本文以车辆段在车站的上行方向为典型情况进行分析。典型渡线设置方式有2种，如图6所示。

a)设置方式一

1)设置方式一。如果上行方向列车发生故障，则故障列车可先由渡线3推送入停车线，待维修恢复正常后，再由渡线4驶出继续沿上行方向运行。如果下行方向的列车发生故障，则故障列车需先推送至站台，再通过渡线1进入停车线，待维修恢复正常后，再由渡线1驶出继续沿下行方向运行。故障列车若无法在短时间内恢复正常，则需在全线停止运营后，由渡线4返回车辆段。

2)设置方式二。如果上行方向的列车发生故障，可从渡线3推送故障列车进入停车线，维修正常后由渡线3至站台折返后才能继续沿上行方向运行，或直接由渡线1驶出沿下行方向运行。如果下行方向的列车发生故障，可从渡线2推送故障列车进入停车线，维修正常后由渡线1驶出继续沿下行方向运行。若故障车短时间内无法恢复正常，需在全线停止运营后，由渡线3至站台折返后返回车辆段。

不同渡线设置方式的运营情况对比见表1。

表1 不同渡线设置方式的运营情况对比表

在运营时段，列车故障救援会影响正线的正常运营，所以对列车进入停车线的时间要求较高。在设计时，除了考虑设置相邻停车线的距离要求外，还应尽量保证上、下行列车均能不通过折返直接进入停车线，从而将正线行车中断时间降到最低。在设置方式二中，上、下行方向的故障列车均能直接驶入停车线，虽然全线停止运营后故障列车返回车辆段需折返，耗时较长，但不影响正线运营，故推荐采用设置方式二。如图6 b)所示，有：

L=L1+2L2+max(L5,L6)+L7

(9)

式中：

L7——渡线2的水平长度。

L7同停车线至左线间距以及道岔选型有关：

L7=dcotα

(10)

结合式(5)和式(6)，可得：

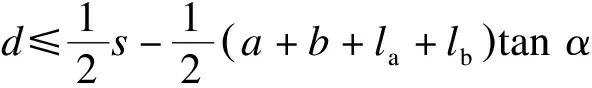
L=L1+2L2+L5+L7=L1+2L2+scotα

(11)

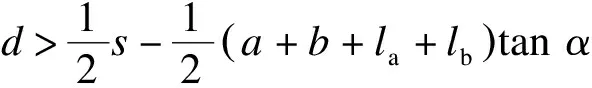
L=L1+2L2+L6+L7=

L1+2L2+2dcotα+a+b+la+lb

(12)

计算可得，在8辆编组A型车、9#道岔的条件下：当d≤0.5s-1.98 m时，L=9s+234.0 m；当d>0.5s-1.98 m时，L=18d+269.6 m。

若按一般车站有效站台宽度为11 m考虑，则s为固定值(14.2 m)时，L-d关系曲线如图7所示。

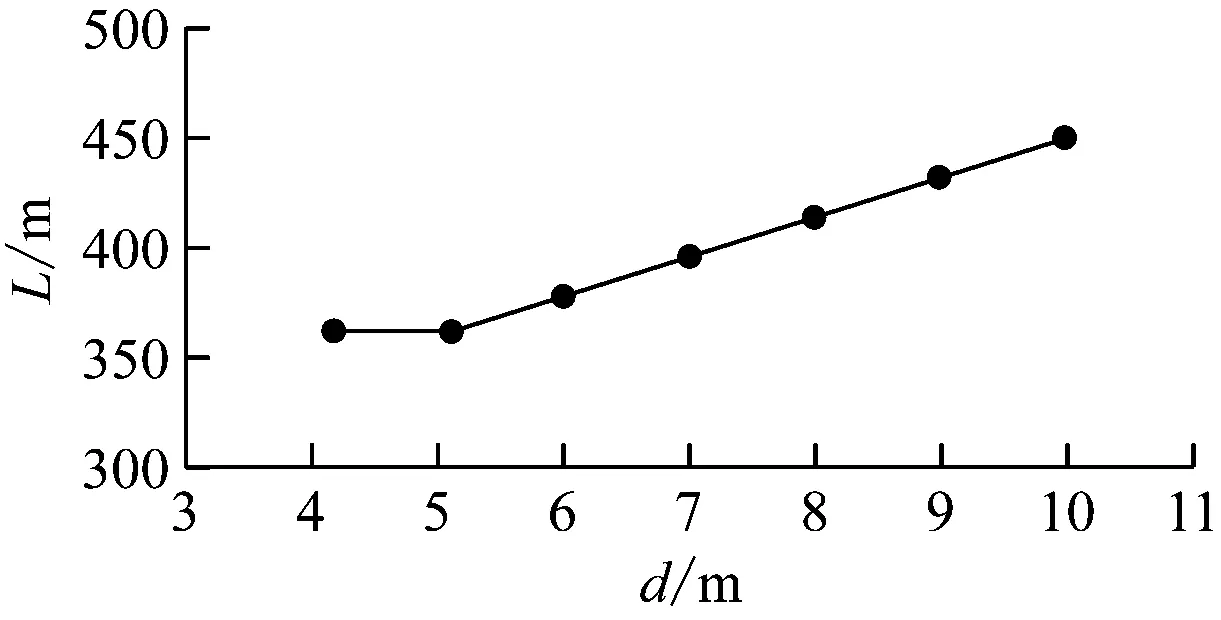
图7 3条渡线单停车线方案L-d关系曲线

由图7，在s=14.2 m的情况下，当d≤5.124 m 时，L=361.8 m，为最小值，则设3条渡线的单停车线方案设计最优。

2.4 取消站台侧安全线的单停车线

设置安全线的主要目的是为了防止停车线上的列车未经允许进入正线、与正线列车发生冲突，或者由于进路没有开通时列车冒进导致列车挤占道岔、而发生列车出轨事故[6]。由于故障列车在进入停车线时的运行速度低，冒进概率小，且同时该区段正线暂停运营，故不存在故障列车与正线列车进路冲突的问题，可取消安全线。停车线纵坡在面向车挡或区间方向为2‰下坡，为防止停车线上的列车溜车，有必要在远离车站的停车线末端设置安全线。综合考虑，为节省工程及简化停车线形式，可考虑取消站台侧安全线，如图8所示。取消站台侧安全线后，有：

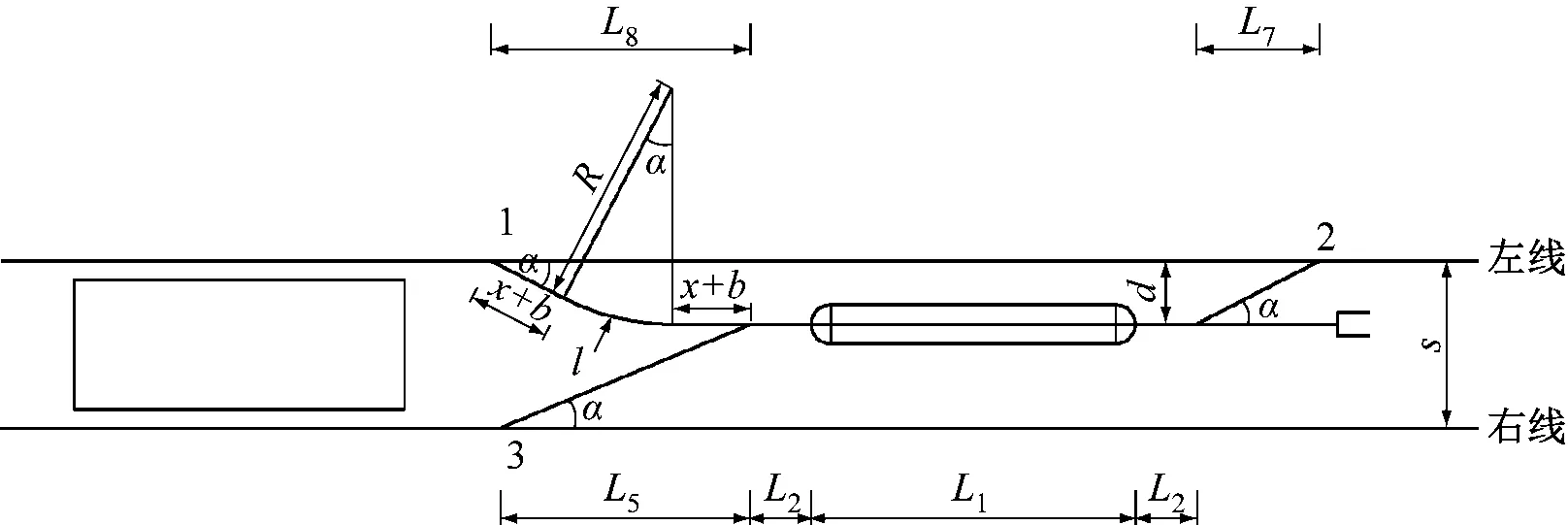
注:R——渡线1曲线半径；x——道岔端部至曲线端部距离；l——渡线1曲线长度

L=L1+2L2+max(L5,L8)+L7

(13)

L8与曲线半径R、道岔端部至曲线端部距离及道岔选型有关：

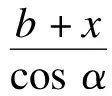
(14)

结合式(5)可得：

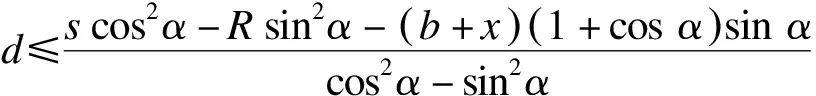
时，

L=L1+2L2+L5+L7=L1+2L2+scotα

(15)

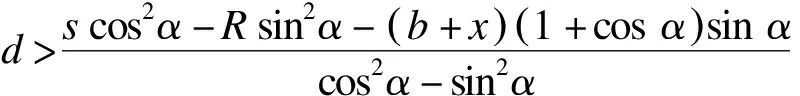
时，

L=L1+2L2+L7+L8=L1+2L2+

(16)

本文按8辆编组A型车、9#道岔的条件进行分析。根据《地铁设计规范》，当采用9#道岔时，道岔端部至平面曲线端或竖曲线端部的距离不应小于5.0 m，则x=5.0 m[1]。由于A型车圆曲线最小长度不宜小于25.0 m，则l≥25.0 m，且R≥225.9 m。

当L5=L8时，d=1.013s-0.013R-4.7 m。R按满足规范的最小半径取整考虑，取226 m。由此，当d≤1.013s-7.5 m时，L=9s+234.0 m，当d>1.013s-7.5 m时，L=8.889d+300.7 m。若按一般车站有效站台宽度为11 m考虑，则s为固定值(14.2 m)时，L-d关系曲线如图9所示。

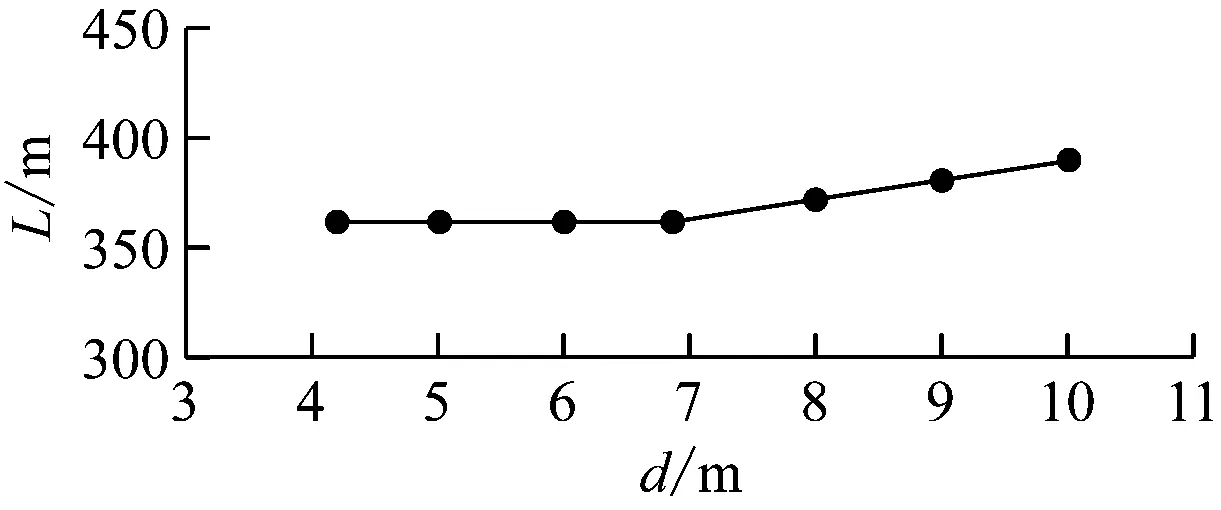
图9 取消站台侧安全线的3条渡线单停车线L-d关系曲线

由图9计算可得，当d≤6.9 m时，L=361.8 m为最小值，且L=9s+234.0 m。

若以渡线1曲线半径作为变量，当L5=L8时，R=81s-80d-374.3 m。当R≤81s-80d-374.3 m时，L=9s+234.0 m；当R>81s-80d-374.3 m时，L=0.111R+312.9 m。若按一般车站有效站台宽度为11 m，s=14.2 m，停车线与左线间距取满足规范的最小值(4.2 m)时，L-R的关系曲线如图10所示。

由图10计算可得：当R≤439.9 m 时，L=361.8 m，为最小值，且L=9s+234.0 m，为最小值。此时的取消站台侧安全线的3条渡线单停车线方案最优。

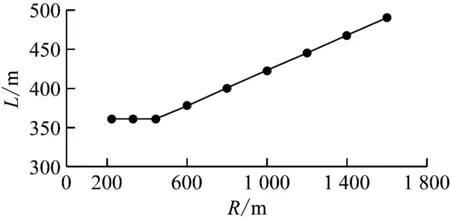
图10 取消站台侧安全线的3条渡线单停车线L-R关系曲线图

3 结语