叠落式同台换乘车站模态及列车振动影响分析

张 戈 王 伟 沈霄云

(北京城建设计发展集团股份有限公司，北京 100034)

叠落式同台换乘车站模态及列车振动影响分析

张 戈 王 伟 沈霄云

(北京城建设计发展集团股份有限公司，北京 100034)

采用模态分析及ISO 10137∶2007评价体系，对杭州地铁某单柱大跨上下叠落式同台换乘车站进行计算分析，得出固有频率为11.9 Hz的第4阶模态和固有频率为41.3 Hz的第20阶模态竖向参振质量较大，同时通过两种不利工况的计算对比可知，地铁列车快速通过车站站台时，其引起的车站各测点的计权加速度均方根值处于较低状态，满足车站各层舒适度要求。

同台换乘车站，模态分析，列车振动，影响

0 引言

同台双向换乘地铁站由于其换乘的便利性，近年来在国内各地地铁建设中得以较广泛的应用。而上下叠落的同台换乘站因其占地面积小、换乘功能好等优点，已在换乘车站中占有相当的比例。

上下叠落的同台双向换乘车站一般设置地下3层，地下1层为站厅层，地下2，3层均为站台层。区别于普通车站，该类车站地下2层楼板有列车行驶其上。

对于单柱大跨上下叠落的同台换乘车站，尚需解决两类问题：1)列车的振动与车站结构是否存在共振的问题。2)在高速列车作用下的站台板、站厅层乘客的舒适度问题。

目前国内尚未见对此类地铁车站该领域的研究，本文以杭州地铁某单柱大跨上下叠落式同台换乘车站为例，针对以上两类问题，通过模态分析、“ISO 10137∶2007评价体系”等进行计算分析，以期解决类似车站结构设计的该类问题。

1 工程概况

杭州地铁某站为上下叠落的4，6号线同台换乘车站。车站主体总长303.5 m，标准段宽26.3 m，地下2，3层站台宽度均为15 m，长度为120 m。车站顶板覆土约为3.3 m，标准段为地下3层单柱箱形框架结构，柱网轴间距为9.0 m。

2 车站模态分析

模态是建筑结构的固有振动特性，每一阶模态具有特定的固有频率、阻尼比和模态振型。模态分析是研究结构动力特性的一种近代方法，通过模态分析，可以了解结构在某一易受影响的频率范围内的各阶主要模态的特性，从而预估结构在此频段内在外部或内部各种振源作用下产生的实际振动响应。

本节拟对本站主体标准断面结构进行二维有限元模态分析，以期得出该结构的敏感频率范围和响应的敏感结构位置。

分析采用大型有限元软件ADINA进行计算模拟，有限元模型如图1所示。

由于不考虑土与结构的耦合作用的建筑振动计算是偏安全的[1]，本次计算有限元计算模型中所有单元均为实体单元，不考虑土与结构的相互作用。模型中地下3层结构底板处按全约束处理，其余各处自由。

计算采用Modal Participation Factor分析当车站结构自振频率为0～580 Hz时，各阶模态参与因子与参振质量情况。其中各阶模态参与因子(即参与系数)随频率变化图如图2和图3所示。

由图2可知，该断面结构水平向振动时，在振动频率为0～10 Hz内的振动模态参与系数较大，其余阶模态参与振动程度较小，可见其水平向振动以自振频率小于10 Hz的相关模态叠加为主。

由图3可知，该断面结构竖向振动时，在振动频率为0～50 Hz 和520 Hz～560 Hz内的振动模态参与系数较大。相比水平向振动，对车站结构竖向振动贡献较大的振动模态分布较为分散。

现考察该断面结构在不同振动频率下的参振质量，进而确定该结构的敏感频率范围和敏感结构位置。其水平向参振质量随频率变化图如图4所示，竖向参振质量随频率变化图如图5所示。

由图4和图5可知，当计算结构固有频率达到580 Hz时，水平向结构累计参振质量达359 t，约占总质量的89.8%，该断面的水平向振动的敏感频率段集中于0～10 Hz的低频范围内。此时，竖向结构累计参振质量达329 t，约占模型总质量的82.3%，竖向振动的敏感频率集中于0～50 Hz的低频段及520 Hz～560 Hz的高频段。

由于车站在列车荷载作用下的振动以竖向振动为主，且隧道结构的固有频率较低，在列车荷载作用下，隧道结构与车站产生共振的频率位于低频段，现就0～50 Hz内车站的振动参振质量进行分析，见图6。

由图6可知，在0～50 Hz内车站竖向参振质量较大(即振动的敏感区域)的位置有两处，分别为固有频率为11.9 Hz的第4阶模态和固有频率为41.3 Hz的第20阶模态，其第4阶和第20阶模态对应的振型图如图7和图8所示。

由图7和图8可知，第4阶振动模态的振型中振动幅度较大的位置主要为站厅层的跨中；第20阶振动模态的振型中振动幅度较大的位置主要为站厅层和地下2层的跨中位置。

由以上的计算结果分析可知，为了防止出现共振现象，在对车站结构进行减振处理时，需要合理选择减振结构的固有频率以避开参振质量比例较大的11.9 Hz和41.3 Hz。

3 轨道振动对车站结构振动的影响分析

3.1 ISO 10137∶2007评价方法

关于在列车振动下人体舒适度的评价标准，国际上主要有ISO 2631及ISO 10137∶2007等[2，3]。

基于本工程特点，本文采取ISO 10137∶2007(全称为《结构设计基础·建筑物和走道防振功能的适用性》)作为人体舒适度评价标准。

ISO 10137∶2007标准提供了两种评价方法：基本评价方法和附加评价方法[4]。

当加速度峰值与计权均方根加速度值之比小于6时，采用基本评价方法，即以计权均方根加速度作为评价指标，将其值与乘以倍乘因子后的曲线进行比较。

评价中主要参量包括：

1)均方根(R.M.S)加速度(m/s2)，其表达式为：

其中，a(t)为某时刻t的加速度，m/s2；T为积分时间。

2)频率计权均方根加速度(m/s2)，其表达式为：

其中，aw(t)为瞬时频率计权加速度，m/s2；T为测量时间长度。若采用数值表示，频率计权均方根加速度表达为：

其中，Wi为第i个1/3倍频带的计权系数；ai为第i个1/3倍频带的加速度均方根值，m/s2。

当加速度峰值与计权均方根加速度值之比大于6时，为考虑荷载冲击效应对振动舒适度的影响，采用振动剂量作为评价指标，将其值与乘以倍乘因子后的曲线进行比较[3]。

本文按最不利工况，即计算时考虑列车快速通过站台。由于未考虑列车进站的减速和出站的加速过程，本次计算可仅采用基本评价方法，即采用计权加速度均方根值aw作为舒适度评价指标(具体计算方法可参详ISO 2631∶2003标准)。

将其值乘以倍乘因子后的曲线进行比较。基本曲线如图9所示，对于连续和间歇振动，具体的倍数见表1。

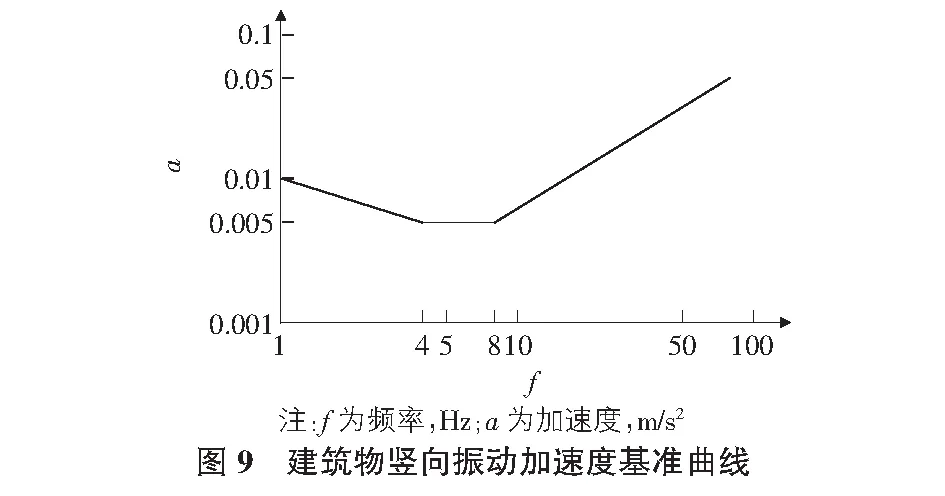
表1 ISO 10137∶2007标准倍乘因子

环境时间倍乘因子严格工作区(如精密实验室，医院手术室等)白天1夜间1住宅(如医院，公寓，别墅等)白天2～4夜间1．4要求较高的办公室，敞开式办公室等白天2夜间2一般办公室(如学校等)白天4夜间4车间白天8夜间8

3.2 计算模型及评价

本处研究对象为地铁车站，属于人群密集区，本身较嘈杂。因此，按表1中第四类(一般办公室)所对应的环境考虑，倍乘因子定为4.0，即在进行舒适度评价时加速度限值取为：仅考虑竖向时为4×5.0×10-3=20 mm/s2。

本站共有4号线左右线、6号线左右线通行。根据列车运行情况，分2种工况进行计算。

工况1：4号线左、右线列车同时通过，6号线无列车通过；

工况2：4号线左、右线列车和6号线左、右线列车同时运行。

本文采取上海地铁列车荷载实测轮轨力曲线图作为荷载输入条件进行计算(见图10)。

结果输出选取车站站厅层及站台层若干测点，具体测点详见图11。

1)工况1计算结果。

在第1种工况中，4号线左、右线同时通过，6号线没有列车通过时，选取车站中的相关测点，计算测点的计权加速度均方根值aw，以评价车站的振动响应情况。各测点计权加速度均方根值aw见表2。

表2 各层节点均方根加速度aw(一) mm/s2

如表2所示，各测点的计权加速度均方根值最大值为0.263 mm/s2，满足标准20 mm/s2，处于较低状态，表明该站的各层满足舒适度要求。速度均方根值和具体取值点有直接关系，相差度较大；而楼层和计算加速度均方根值区相关性不大。

2)工况2计算结果。

在第2种工况中，4号线左、右线和6号线左、右线列车同时运行，选取车站中的相关测点，计算测点的计权加速度均方根值aw，以评价车站的振动响应情况。各测点计权加速度均方根值aw如表3所示。

表3 各层节点均方根加速度aw(二) mm/s2

如表3所示，各测点的计权加速度均方根值最大值为0.276 mm/s2，满足标准20 mm/s2，处于较低状态，表明该站的各层满足舒适度要求。速度均方根值和具体取值点有直接关系，相差度较大；楼层和计算加速度均方根值区相关性不大。

4 结语

通过以上对杭州地铁某单柱大跨上下叠落式同台换乘车站进行计算分析，主要结论如下：

1)通过对车站典型断面进行模态分析，得到结构水平向振动时，在振动频率为0～10 Hz内的振动模态参与系数较大，其余阶模态参与振动程度较小。

结构竖向振动时，在振动频率为0～50 Hz和520 Hz～560 Hz内的振动模态参与系数较大。

2)列车引起的振动以竖向振动为主，在0～50 Hz内车站竖向参振质量较大(即振动的敏感区域)的位置有两处，分别为固有频率为11.9 Hz的第4阶模态和固有频率为41.3 Hz的第20阶模态。

为了防止出现共振现象，在对车站结构进行减振处理时，需要合理选择减振结构的固有频率以避开参振质量比例较大的11.9 Hz和41.3 Hz。

3)利用ISO 10137∶2007评价方法，通过两种不利工况的计算对比可知，地铁列车快速通过车站站台时，其引起的车站各测点的计权加速度均方根值最大值为0.276 mm/s2，满足标准20 mm/s2，处于较低状态，表明该站的各层满足舒适度要求。

[1] 王田友.地铁运营所致环境振动及建筑物隔振方法研究[D].上海:同济大学，2007.

[2] 赵 娜.地铁上盖物业的振动舒适度研究[D].武汉:武汉理工大学，2012.

[3] 王国波，谢伟平，于艳丽，等.高速列车引起的武汉站楼板振动舒适度研究[J].振动与冲击，2010,29(12):39-41.

[4] 周德良，李爱群，周朝阳，等.长沙南站大跨度候车厅楼盖竖向舒适度分析与检测[J].建筑结构,2011,41(7):98-100.

Analysis on shifted-style cross-platform interchange modal and train vibration influence

Zhang Ge Wang Wei Shen Xiaoyun

(BeijingCityConstructionDesignDevelopmentGroupCo.,Ltd,Beijing100034,China)

Applying modal analysis and ISO 10137∶2007 evaluation system, the paper calculates and analyzes single-column large-span shifted-style cross-platform interchange of Hangzhou subway, and concludes that: the vertical vibration quality is bigger of fixed frequency 11.9 Hz at the 4th modal phase and fixed frequency 41.3 Hz at the 20th modal phase, through calculation and comparison of two kinds of adverse conditions, the subway train fast through the station, the station accelerated speed point lies in low statement which meets comfort demands.

cross-platform interchange, modal analysis, train vibration, influence

2015-02-10

张 戈(1982- )，男，工程师

1009-6825(2015)11-0132-03

U231.4

A