基于遗传算法的多层介质平板厚度优化设计
苏京文, 刘元云
(上海无线电设备研究所,上海200090)
0 引言
多层电介质平板结构有A 夹层、B夹层、C夹层等类型[1-2]。A 夹层结构由两层高介电常数的表面层和低介电常数的中间芯层组成;B 夹层结构是由两层低介电常数的表面层和高介电常数的中间芯层组成;C夹层结构是由两层A 夹层结构组合而成,即由五层介质构成。相比A 夹层和B夹层,C夹层结构具有更宽的频带特性,并且可以在大的入射角范围内获得较好的传输特性[3-4],可用于高速流线罩[5-6]。本文使用传输线理论分析多层平板的透波系数和反射系数[7],并结合实例,用遗传算法对C 夹层介质平板进行厚度优化[8],并依据最佳厚度计算了该C 夹层结构的透波系数与反射系数。
1 多层介质平板的电性能分析
分析电磁波穿过介质平板的传输问题时,可以把介质平板外表的两侧空间当作空间传输线,两侧自由空间的波阻抗为Z0,并且把介质平板的各个介质层看作特性阻抗各异的传输线,式(1)为介质层的传输线特性阻抗。
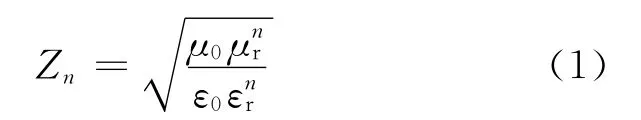
式中:Zn为第n 层介质的特性阻抗;ε0和μ0 是自由空间的介电常数和导磁率;εnr和μnr是第n层介质材料的相对介电常数和相对导磁率。
对于多层电介质平板,可以将相互叠加的各个夹层等效为多个四端口网络的级联形式,前一级网络的输出恰好是后一级网络的输入。网络的级联矩阵为各级矩阵的乘积。式(2)为具有n 层结构介质平板的级联矩阵方程。
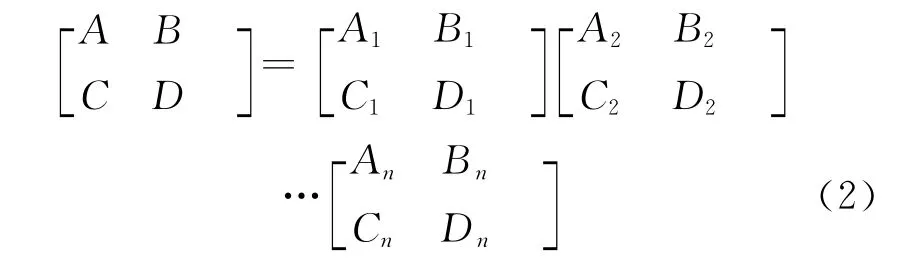
其中:
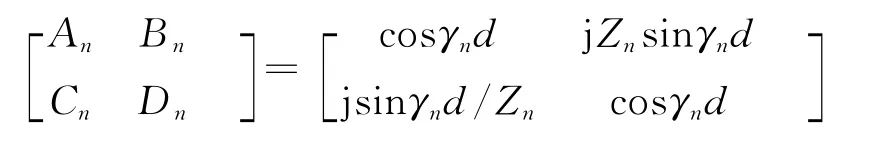
式中:γn为传输线的传播常数(与入射电磁波的极化方向、入射角以及平板所用材料的介电常数与损耗常数有关);d 为多层电介质平板总厚度。
根据级联矩阵的定义[1],可以推导出多层电介质平板的反射系数和透波系数分别为
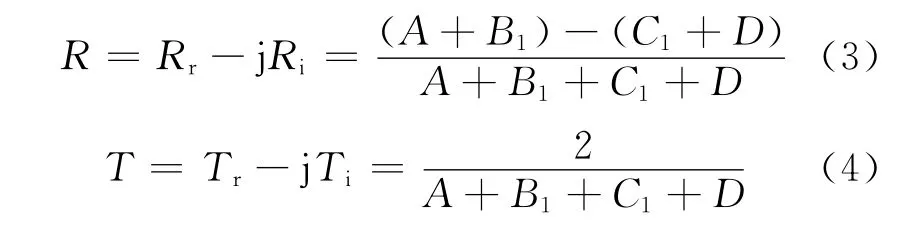
式中:B1=B/Zn;C1=C/Zn;A、B、C 和D 为级联矩阵元素。
2 多层介质平板厚度优化设计
对多层介质平板的厚度进行优化设计时,可以把各夹层的厚度看作是待优化参数。通过改变各夹层厚度可以改变多层介质平板的传输、反射特性。从而可以将多层介质平板的厚度设计问题转换为多参数优化问题。
遗传算法(Genetic Algorithm)是通过模拟自然界生物的进化过程,对目标函数进行全局性最优解搜索的一种高效优化算法。
遗传算法由于具有鲁棒性、普适性、并行性以及全局搜索等特点使特别适合于解决大规模复杂系统的优化问题。因此,选择遗传算法对多层介质平板进行优化设计。
2.1 设计方法
(1)编码方式
遗传算法中的二进制编码是最简单的编码方式之一,它的编码符号集是由二进制符号0 和1所组成的二值符号集{0,1},它所构成的个体基因型是一个二进制符号串。在对多夹层电介质平板进行编码时,一个二进制符号串对应一个夹层的厚度值。
(2)自适应函数选取
遗传算法中自适应函数用于评价个体的优劣程度。自适应函数的变量为多参数优化问题中的待优化参数,即多夹层平板中各夹层的厚度。自适应函数值即优化问题中的目标函数值,由于透波系数是表征多层电介质平板传输特性优劣的重要参数,因而以最大透波系数为设计目标时应选取透波系数作为遗传算法的适应度函数值。为了加快优化速度,引入优化因子:

式中:a,b是优化因子,为常数,取a=2.5,b=-1。
(3)遗传操作
遗传操作包括选择、交叉和变异三种基本操作。
①选择
选择操作的目的是把优化的个体直接遗传到下一代,或通过配对交叉产生新个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。本文选用的适应度比例法是最基本也是最常用的一种选择方法。在该方法中,各个个体的选择概率与适应度值成比例。设群体大小为n,其中个体i的适应度值为fi,则个体i的选择的概率为
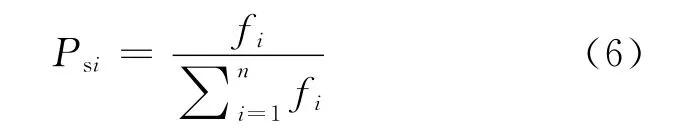
从式(6)中可以看出,概率Psi反映了个体i的适应度在整个群体的个体适应度总和中所占的比例。个体适应度越大,被选择的概率就越高,反之亦然。
②交叉
交叉是遗传算法中产生新个体的主要方法。交叉是指两个相互配对的染色体按照某种方式以交叉概率相互交换部分基因,从而形成两个新的个体。交叉的过程如图1所示。
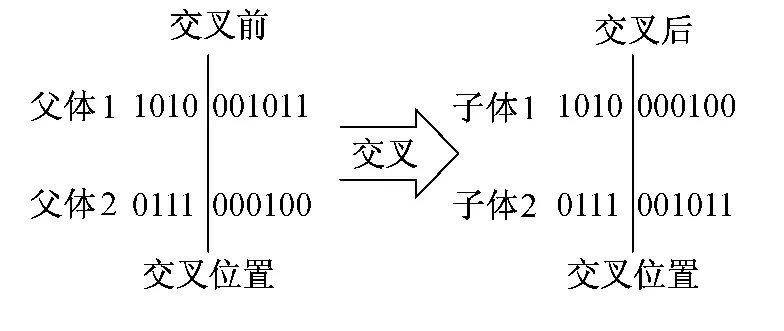
图1 交叉过程示意图
交叉操作时,随机选择一对染色体上的某一等位基因,并将相应的部位对调,产生一对新的染色体。通过交叉操作可以生成大量新的夹层厚度数值,以便在下一轮的遗传优化中作为主要的选择样本。
③变异
变异是将群体中的个体串的某些基因座上的基因值作变动。对于以二进制编码的码串,变异操作就是把某些基因座上的基因值取反。变异操作的基本过程:
a)首先在群体内所有个体的码串中随机地确定基因座;
b)然后以事先设定的变异概率对这些基因座的基因进行变异。
变异操作的目的是改变各夹层厚度,生成新的待优化参数。
2.2 设计举例
以某种C 夹层介质平板为例,它是由外蒙皮、芯层、中间蜂窝层以及胶膜材料构成的平板结构,工作频率为2GHz~18GHz,电磁波对平板入射角范围为0°~45°。
设定材料电参数:蒙皮与芯层材料相同,介电常数为3.3,损耗角正切为0.008,厚度优化范围为0.5mm~2.0mm;胶膜材料介电常数为3.2,损耗角正切为0.006,厚度为0.1mm;蜂窝材料介电常数为1.1,损耗角正切为0.005,厚度优化范围为2.0mm~10.0mm。
在使用遗传算法进行参数优化计算时,编码串长度取10 位二进制数,选择种群大小为150,交叉概率为0.9,变异概率为0.01,终止代数为100。选择5个频率点,且对每个频率点取6个角度点,即利用30 个采样点对各夹层厚度进行设计,计算结果如表1所示。
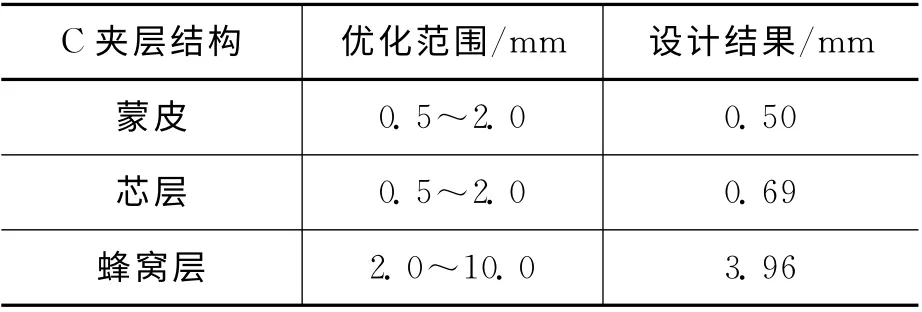
表1 C夹层平板结构的设计结果
3 仿真分析
为了验证设计结果,分别对垂直与水平极化入射时的透波系数和反射系数进行计算。
图2(a)与图2(b)分别表示电磁波分别以垂直极化与水平极化入射时,透波系数随入射电磁波频率的变化关系。
由图2可见:对于垂直极化入射波,透波系数在整个频率范围内变化较为剧烈,且入射角度越大,变化幅度越大,在整个频率范围内透波系数均大于0.90;对于水平极化入射波,透波系数在0.96以上。
图3(a)与图3(b)分别表示电磁波以垂直极化与水平极化入射时,透波系数随入射角的变化关系。
由图3可见:对于以垂直极化方式入射的电磁波,透波系数在入射角度小于45°时在0.92以上;对于水平极化入射波,透波系数在0.96以上,且随入射角度变化幅度很小。
图4(a)与图4(b)分别为电磁波以垂直极化与水平极化入射时,反射系数随入射电磁波频率的变化关系。
由图4可见:对于垂直极化入射波,反射系数小于0.08;对于水平极化入射波,反射系数小于0.03。
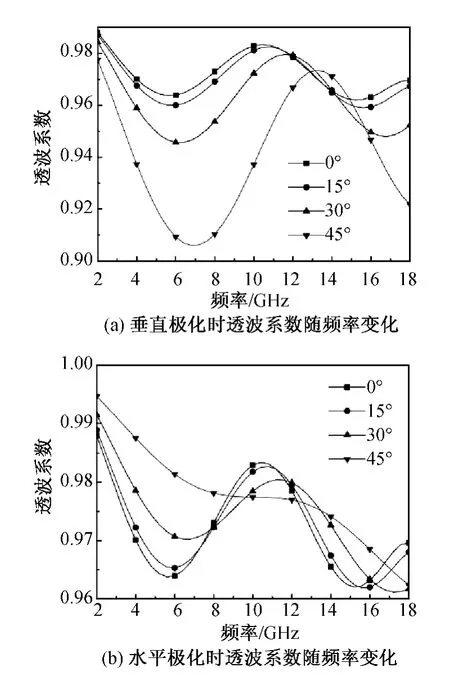
图2 透波系数随频率变化计算结果曲线
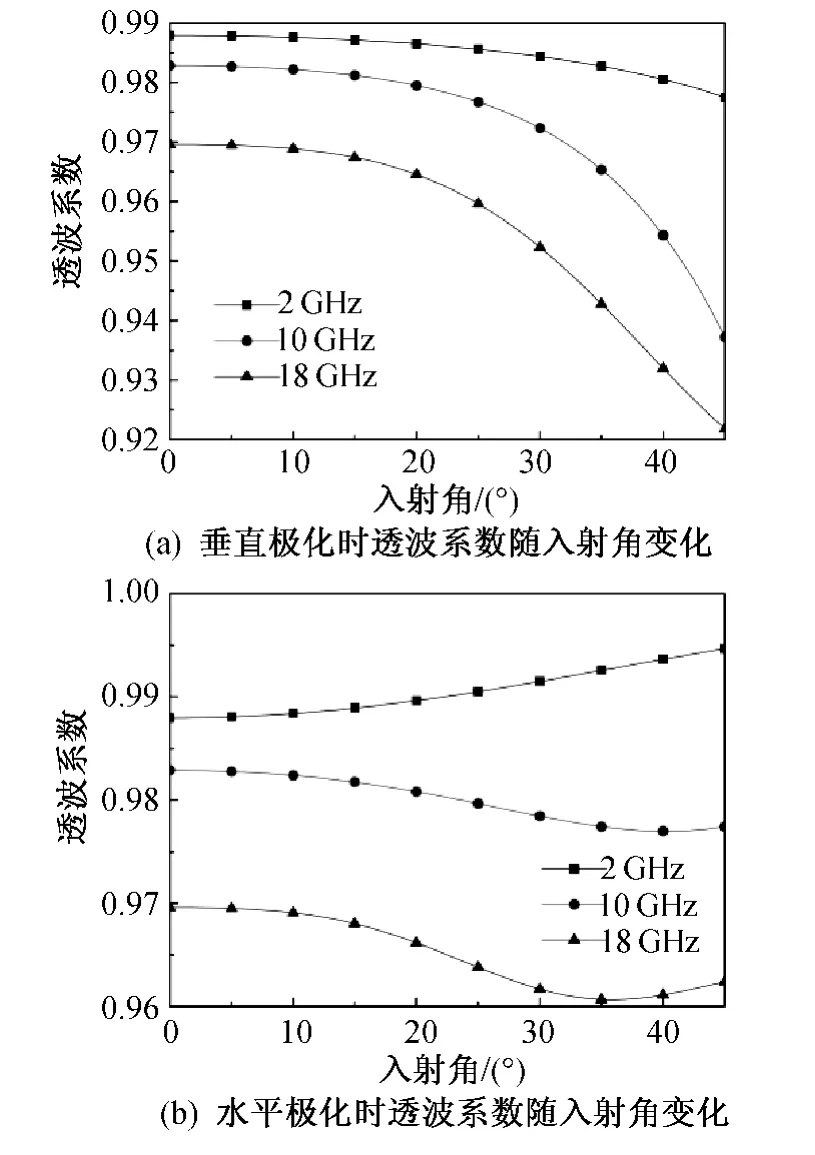
图3 透波系数随入射角变化计算结果曲线
图5(a)与图5(b)分别表示电磁波以垂直极化与水平极化入射时,反射系数随电磁波入射角度的变化关系。

图4 反射系数随频率变化计算结果曲线
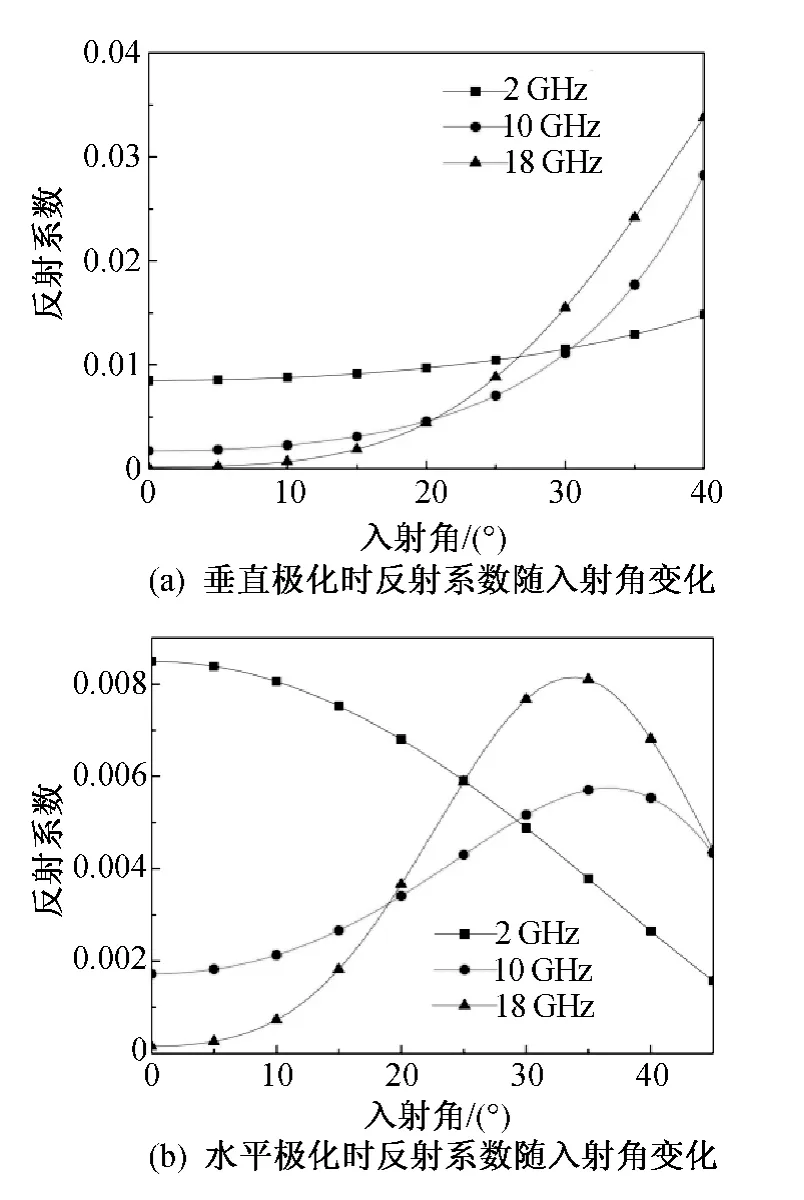
图5 反射系数随入射角变化计算结果曲线
由图5可见:对于以垂直极化方式入射的电磁波,反射系数在0.035以下;对于水平极化入射波,反射系数在0.01以下。
4 结论
综上所述,多层电介质平板在设定的工作范围内,透波系数约为0.96,最小值不低于0.90;反射系数约为0.03,最大值不超过0.08。多层电介质板将在导弹天线罩中将获得应用。
[1] 杜耀惟.天线罩电信设计方法[M].北京:国防工业出版社,1993.
[2] 张运尚.天线—罩系统电性能数值分析与优化研究[D].大连:大连理工大学,2013.
[3] Chen Hong-yu,Shen Zhong-xiang,and Li E.Analysis of a three-dimensional antenna radiating through a two dimensional radome using a fast hing-order method[J].IEEE Transactions on Magnetics,2006,42(4):699-702.
[4] Abdel Moneum M.A.Hybrid PO-MOM Analysis of Large Axi-Symmertic Radome[J].IEEE Transactions on Antennas and Propagation,2001,49(12):1657-1666.
[5] 万国宾,万伟等.雷达罩电性能的优化[J].系统工程与电子技术,2000,(5):40-42.
[6] 傅文斌,陈忠宽,等.夹层天线罩电性能的多目标遗传优化[J].电波科学学报,2005,(3):289-294.
[7] 董金明,林萍实.微波技术[M].北京:机械工业出版社,2003.
[8] 唐文艳.结构优化中的遗传算法研究和应用[D].大连:大连理工大学,2002.
——以渤海A 油藏为例

