相控阵雷达导引头捷联解耦技术研究
杨建锋
(燎原无线电厂,四川 成都610100)
0 引言
相控阵天线具有扫描速度快、天线波束形状变化迅速、空间功率合成能力强等特点,这些技术特点使得相控阵雷达获得广泛应用[1-2]。导引头是精确制导武器系统的核心部件,通过接收目标辐射或反射的特征能量,确定目标参数,送给弹上控制系统形成制导信号,控制导弹飞向目标;导引头主要性能指标是跟踪速度与跟踪精度[3-4]。在纯稳定状态下,由于弹体扰动引起导引头天线空间指向变化,影响了导引头对目标的跟踪效果,为了保证相控阵雷达导引头对目标持续稳定测量与跟踪,需要一个能隔离弹体扰动、稳定精度高的捷联解耦系统。文献[5]和文献[6]在分析相控阵雷达导引头技术特点的基础上详细推导了捷联解耦算法。文献[7]和文献[8]利用惯导系统提供弹体姿态角,通过坐标变换,根据波束指向在惯性空间不变性原则,实施角度补偿隔离弹体扰动。文献
[9]设计了一种相控阵雷达导引头波束稳定的方法,无需精确的初始姿态,由角速度传感器和信号处理机组成独立模块,通过解算得到补偿角,控制波束指向实现捷联解耦。以上算法均需要惯导系统提供弹体初始姿态信息,增大了武器系统的准备时间,并且在波束稳定过程中需要进行姿态角实时计算。虽然文献[9]无需精确的初始姿态信息,但是要求雷达开机前弹体保持小角度运动,也需要解算弹体姿态角,计算量较大。
本文基于天线波束指向在惯性空间不变性原则,设计了一种相控阵雷达导引头捷联解耦算法,给出了数学仿真结果。通过设计天线坐标系中任意单位向量,推导出基于不变性原理的一般方程,根据姿态矩阵与四元数的等价关系,运用四元数来表述一般方程,约去姿态四元数,计算得到实时框架角,利用波束控制实现捷联解耦。该方法无需惯导系统初始对准,不用实时计算弹体姿态角,工程上易于实现,数学仿真结果表明隔离度可以满足工程应用要求。
1 坐标系
相控阵雷达导引头捷联解耦采用的坐标系定义如下[10]:
a)惯性坐标系——原点Oi在导弹发射点,OiXi轴在发射点的水平面内,指向发射方向,OiYi轴沿发射点的铅垂线向上,OiZi轴垂直于OiXiYi平面,方向按右手定则确定;
b)弹体坐标系——原点Om为弹质心,OmXm轴与弹体纵对称轴一致,指向弹头方向,OmYm轴在弹体纵对称面内,垂直OmXm轴,指向上为正,OmZm轴垂直于OmXmYm平面,构成右手系;导弹相对惯性坐标系下的三个姿态角分别为偏航角ψ,俯仰角φ,滚动角γ;旋转顺序为先偏航角、再俯仰角、然后滚动角;弹体坐标系到惯性坐标系的姿态矩阵为Cim(ψ,φ,γ);
c)天线坐标系——原点Oa取在导引头旋转中心上,OaXa轴沿天线测量敏感轴方向,指向目标为正;OaYa轴位于OaXa轴垂直平面内,指向上为正,OaZa轴垂直于OaXaYa平面,方向按右手定则确定;天线波束相对弹体坐标系下的两个框架角分别为框架方位角λy,框架俯仰角λz;旋转顺序依次为框架方位角、框架俯仰角。
天线坐标系到弹体坐标系转换矩阵:
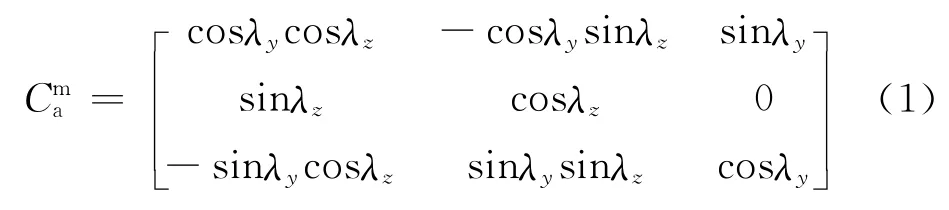

其中:

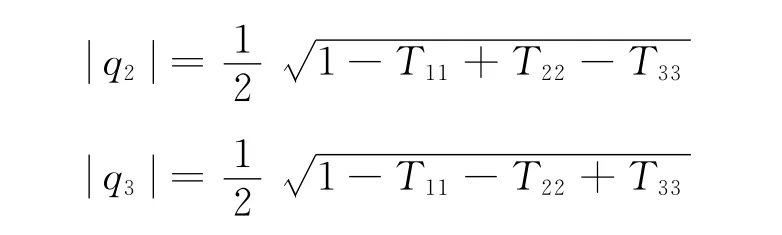
实际计算中,q0取正值,q1、q2、q3符号按下式确定:

2 捷联解耦原理
在弹体扰动的情况下,要求天线波束指向在惯性空间保持不变。惯性测量单元实时测量弹体角速度信息,结合当前解耦周期在弹体坐标系下天线波束指向,推导下一解耦周期在弹体坐标系下天线波束指向,进而得到天线补偿角,通过控制天线波束指向,消除弹体扰动的影响,保持天线波束在惯性空间指向不变,实现捷联解耦。
设导弹发射时天线波束指向目标方向,取天线坐标系单位矢量U0=[α β τ]T,该单位矢量在tk-1时刻惯性坐标系中的瞄准线向量为[13]
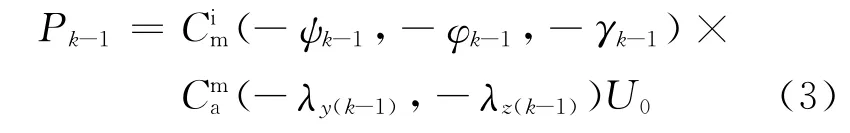
式中:ψk-1、φk-1、γk-1分别为tk-1时刻弹体偏航角、俯仰角、滚动角;λy(k-1)、λz(k-1)分别为tk-1时刻框架方位角、框架俯仰角。
在tk时刻U0=[α β τ]T在惯性坐标系中的瞄准线向量为
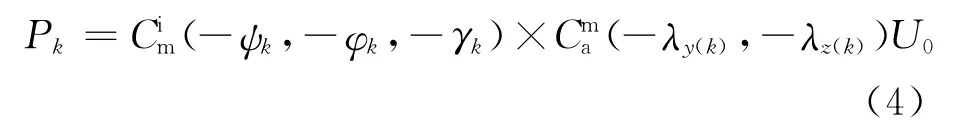
式中:ψk、φk、γk分别为tk时刻弹体偏航角、俯仰角、滚动角;λy(k)、λz(k)分别为tk时刻框架方位角、框架俯仰角。由捷联解耦原理可得

即
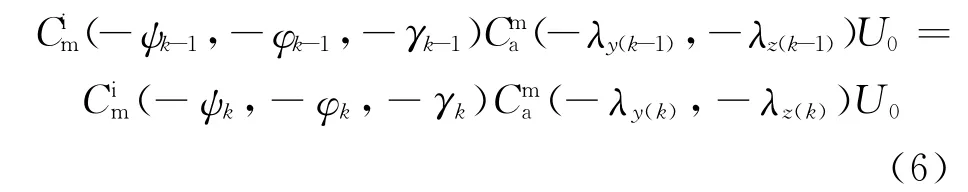
由单位矢量U0=[α β τ]T的任意性得

由姿态阵与四元数之间的等价关系[11],可得与式(7)对应的四元数为

式中:Q(tk)、Q(tk-1)分别称为tk时刻和tk-1时刻的姿态四元数;q(tk)、q(tk-1)分别称为tk时刻和tk-1时刻的框架四元数。
在捷联解耦周期h=tk-tk-1,有

式中:p(h)称为一个解耦周期的姿态变化四元数。结合式(8)和式(9)有
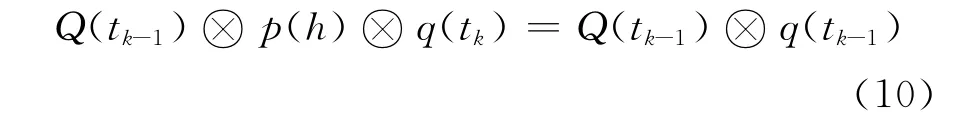
姿态矩阵是正交阵,姿态矩阵可逆,根据姿态阵与四元数的等价关系,姿态四元数亦可逆,因此可得

同理,姿态变化四元数也可逆,则式(11)可以写为
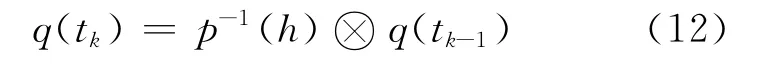
式中:p-1(h)为姿态变化四元数p(h)的逆。一般地,求取框架四元数后,要求对框架四元数进行规范化,式(12)可以简化为
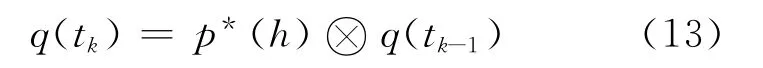
式中:p*(h)为姿态变化四元数p(h)的共轭四元数。求得框架四元数后,计算实时框架角:
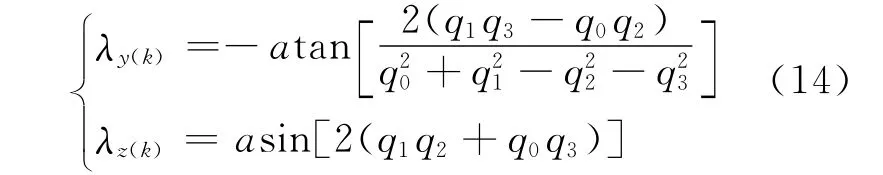
得到消除弹体扰动的实时天线补偿角[14-15]:
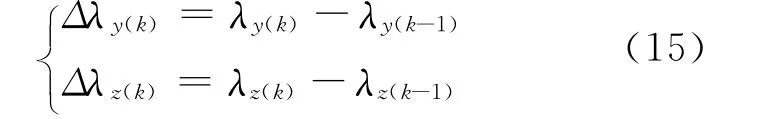
由此可知,为消除弹体扰动的影响,捷联解耦与弹体初始姿态无关。在计算框架四元数的过程中,无需求取弹体姿态角,只需进行框架四元数更新,从而计算实时框架角,得到天线补偿角,实现捷联解耦。因此,相控阵雷达导引头在捷联解耦过程中,无需进行初始对准,缩短了武器系统准备时间,该算法简单,计算量小,易于工程实现。
3 实现过程
相控阵雷达导引头为消除弹体扰动,通过惯性测量单元测量的弹体角速度更新框架四元数,从而更新框架角,实现天线波束指向在惯性空间保持不变。该算法需要的输入信息:
a)初始时刻框架方位角和框架俯仰角;
b)实时弹体角速度信息ωx、ωy、ωz。
3.1 初始化
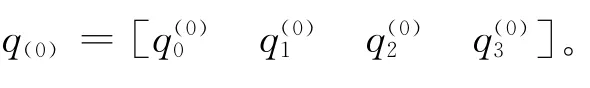
3.2 实时框架角
通过当前时刻tk弹体姿态变化四元数的共轭四元数与上一时刻tk-1框架四元数q(tk-1)相乘,得到当前时刻tk框架四元数q(tk),通过反三角函数计算当前时刻tk框架方位角λy(k)和框架俯仰角λz(k)。设惯性测量单元在时刻t1、t2测量得到弹体角速度矢量分别为ω1、ω2,则根据等效旋转矢量的二子样算法,可得
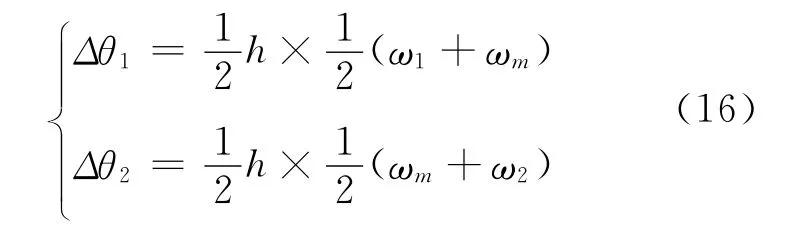
其中:

由式(16)得等效旋转矢量为
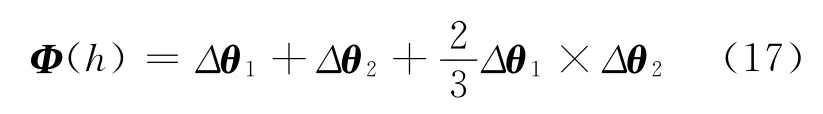



3.3 捷联解耦天线补偿角
根据上一时刻的框架方位角λy(k-1)、框架俯仰角λy(k-1),结合当前时刻框架方位角λy(k)、框架俯仰角λz(k),利用式(15)计算消除弹体扰动的天线补偿角Δλy(k)、Δλz(k)。
4 数学仿真分析
相控阵捷联导引头捷联解耦可以利用隔离度衡量解耦效果。隔离度是捷联解耦的主要指标,计算式为

式中:Δε 为惯性空间中天线波束指向变化的幅值;Δθ 为弹体扰动角度幅值。
隔离度越小,平台对弹体扰动的隔离能力越强,导引头能达到的稳定精度越高。
设天线初始框架角λy(0)=λz(0)=0,弹体偏航、俯仰和滚动扰动角度幅值均为3°,频率为3Hz。捷联解耦周期是10 ms,即每10 ms完成一次补偿角求取,不考虑系统传输延时和天线控制周期,进行捷联解耦,该状态对应弹体初始姿态角均为0°,数学仿真结果曲线如图1和图2所示。
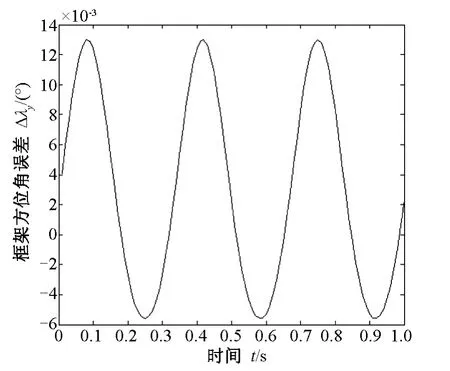
图1 初始姿态角为0°时框架方位角误差
由图1和图2可以看出,初始框架角均为0°,框架方位角误差变化幅值为0.013°,框架俯仰角误差变化幅值为0.015°,因此隔离度为0.5%。
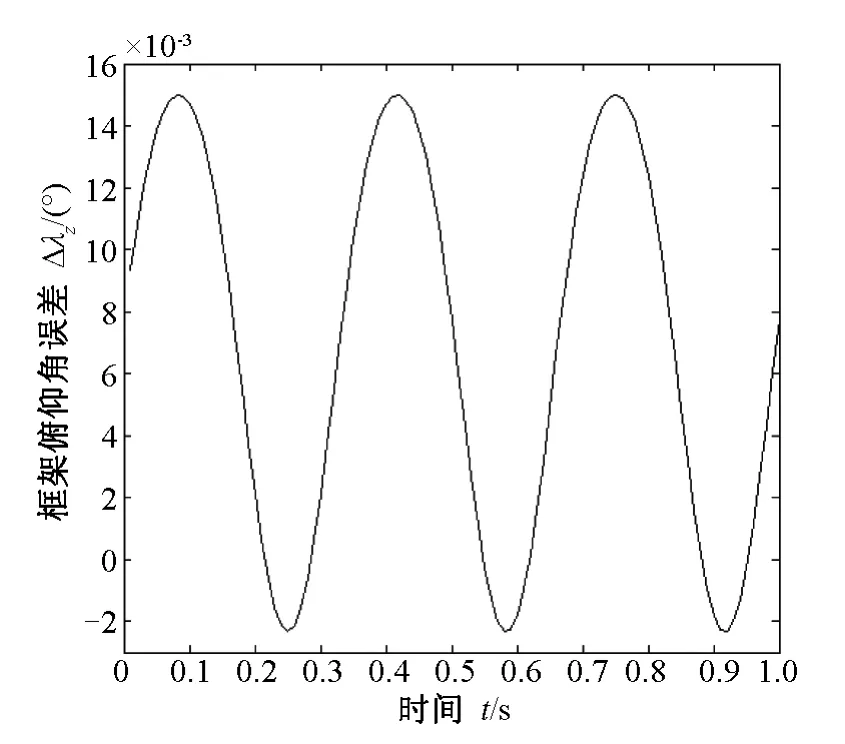
图2 初始姿态角为0°时框架俯仰角误差
为验证捷联解耦无需初始对准,设天线初始框架角为λy(0)=-2.26°,λz(0)=-2.81°,进行捷联解耦,数学仿真结果如图3和图4所示。该状态对应弹体初始滚动角为5°,偏航角为2°,俯仰角为3°。
由图3 和图4 可以看出,当初始框架角为λy(0)=-2.26°,λz(0)=-2.81°,框架方位角误差变化幅值为0.015°,框架俯仰角误差变化幅值为0.013°,因此隔离度为0.5%。
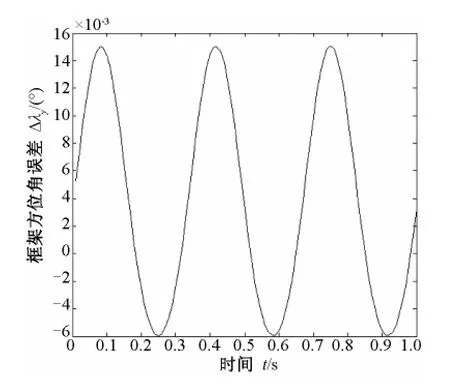
图3 初始姿态角不为0°时框架方位角误差
从图1到图4的仿真结果可以看出,给定不同初始框架角,捷联解耦隔离度可以满足小于5%的工程应用要求。为验证捷联解耦效果,选取不同的扰动参数,设天线初始框架角为λy(0)=λz(0)=0°,弹体偏航、俯仰和滚动扰动角度幅值均为3°,频率为3Hz。捷联解耦周期是5 ms,进行捷联解耦,数学仿真结果如图5和图6所示。

图4 初始姿态角不为0°时框架俯仰角误差

图5 框架方位角误差(扰动频率3Hz,解耦周期5ms)

图6 框架俯仰角误差(扰动频率3Hz,解耦周期5ms)
由图5和图6可以看出,初始框架角均为0°,扰动频率3Hz,解耦周期5ms,框架方位角误差变化幅值为0.002 6°,框架俯仰角误差变化幅值为0.003 2°,因此隔离度为0.1%。
设扰动频率为5 Hz,其余仿真条件不变,进行捷联解耦,数学仿真结果如图7和图8所示。

图7 框架方位角误差(扰动频率5Hz,解耦周期5ms)

图8 框架俯仰角误差(扰动频率5Hz,解耦周期5ms)
由图7和图8可以看出,初始框架角均为0°,扰动频率5 Hz,解耦周期5ms,框架方位角误差变化幅值为0.008 4°,框架俯仰角误差变化幅值为0.009 9°,因此隔离度为0.3%。
从仿真结果分析,捷联解耦周期越短,弹体扰动频率越低,隔离度越小。
5 结论
本文基于二子样等效旋转矢量法提出了一种相控阵雷达导引头捷联解耦方法,得出结论如下:
a)初始对准是惯导系统的一个十分重要的问题,对于需要快速反应的武器系统,要求进行快速和高精度初始对准,本文推导的算法无需进行初始对准,为武器系统快速反应节省了时间;
b)解耦过程中,无需计算弹体姿态角,只需计算由天线框架角构成的转换矩阵对应的四元数,就可以完成捷联解耦,因此算法简单,计算量小;
c)通过仿真验证,导引头隔离度小于5%,可以满足捷联解耦工程应用要求;比较仿真结果,解耦周期短,扰动频率低,得到解耦隔离度小。
[1] 张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2006:27-31.
[2] Mancuso Y,Gremillet P,Lacomme P.T/R Modules Technological and Technical Trends for Phased Array Attennas[J].IEEE MTT-S International Microwave Symposium Digest,2006:614-617.
[3] 赵超.导引头稳定系统隔离度研究[J].电光与控制,2008,15(7):78-82.
[4] 毛峡,张俊伟.半捷联导引头光轴稳定的研究[J].红外与激光工程,2007,36(1):9-12.
[5] 李秋生.相控阵雷达导引头捷联去耦技术研究[J].制导与引信,2005,26(2):19-22.
[6] 孙彪.相控阵雷达导引头捷联去耦数字平台设计[J].电子设计工程,2012,20(13):79-82,85.
[7] 穆虹.防空导弹雷达导引头设计[M].北京:宇航出版社,1996:396-406.
[8] 周瑞青,刘新华,史守峡.捷联导引头稳定与跟踪技术[M].北京:国防工业出版社,2010:116-118.
[9] 李阳,肖增义,孙芃.相控阵雷达捷联波束稳定方法[J].航空学报,2014,35(2):497-505.
[10] 张平,董小萌,付奎生.机载/弹载视觉导引稳定平台的建模与控制[M].北京:国防工业出版社,2011:59-65.
[11] 秦永元.惯性导航[M].北京:科学出版社,2007:303-317.
[12] 周江华,苗育红,肖刚.捷联惯导系统初始四元数提取的新算法[J].飞行力学,2003,21(3):63-66.
[13] 贾筱媛,赵超.半捷联稳定控制方案与制导信息提取方法[J].红外与激光工程,2011,40(12):2474-2479.
[14] Gusinsky V Z,Lesyuchevsky V M,Litmanovich Y A.New Procedure for Deriving Optimized Strapdown Attitude Algorithms[J].Journal of Guidance,Control and Dynamics,1997,20(4):673-680.
[15] 王琪,付书堂.相控阵雷达导引头捷联波束稳定算法研究[J].航空兵器,2011,(6):3-5.

