基于多网络体系分析的城市交通系统脆弱性研究＊

刘 伟 王奥博

（重庆交通大学交通运输学院 重庆 400074）

0 引 言

随着我国城市化进程不断加快，城市规模与机动化水平迅速提升，同时日益复杂的城市交通系统也产生诸多问题.近几年来，我国大中型城市多次出现交通系统某一部分受到异常影响进而导致整个路网功能性瘫痪的情况，如2013年5月12日重庆市观音桥环道窨井盖塌陷，迅速引发了重庆市北部新区路网的严重拥堵，2013年中秋节居民出行激增，导致机场路拥堵并迅速蔓延至整个机场快速路［1］.大范围交通系统级联失效不仅造成了拥堵引发损失，也延缓了应急救援与修复的进度，形成恶性循环.因此开展交通系统的脆弱性分析对提升整个交通系统运行稳定性，改善交通系统抗风险冲击能力，保障城市正常功能有着重要意义.

目前国内外学者开展了大量城市路网脆弱性的分析研究.Beridca最早提出了有关路网脆弱性的定义，他认为交通网络脆弱性是一个易受事件影响而导致路网服务水平极度下降的敏感系数［2］.Scott［3－5］等运用运输绩效、广义出行成本的方式对交通网络运行角度对路网脆弱性做出了进一步的研究.我国学者张勇等［6］引入了道路网络鲁棒性并引入通行能力约束进行脆弱性分析.近年来，复杂网络科学的迅速发展对宏观交通系统特性分析起到了巨大促进作用，并形成了一系列研究成果［7］，其中对于相互依存网络的鲁棒性分析［8－10］为研究复杂交通系统的脆弱性提供了基础.本文以相互依存网络鲁棒性为基础，将交通系统抽象化为复杂网络体系以研究复杂城市交通系统脆弱性特征.

1 交通系统的多网络体系抽象化

城市交通系统瘫痪的原因多种多样，地震、台风等异常天气或交通突发事件等对交通系统产生的影响并不局限于道路网络层面，而是更广泛的存在于交通系统参与的每一个环节.因而，交通系统的脆弱性是集合了路网脆弱性、交通需求脆弱性［11］，以及包含了诱导、组织，等等措施影响的交通管理脆弱性的一个整体性概念.因而将多种宏观影响抽象化为复杂网络并组成复杂网络体系是研究交通系统整体性质的基础.

城市道路网络、交通需求网络的特征已有大量研究［12－13］.对于包含交通诱导、交通组织的交通管理措施在以往研究中往往视为道路网络的属性.但在实际情况中交通干预并不完全与道路网络吻合，而是具有自己的拓扑结构与网络特性.考虑到交通干预的作用方式，可将其视为部分路网节点的联系（增强或减弱其通行能力），而通常这种联系是相邻网络节点且每个节点联系数目相差不多.由此，分析交通管理网络度分布得出其近似泊松分布，可说明其符合随机网络特性.

对于道路网络的抽象化而言，如果仅从道路拓扑结构来分析其可达性，无法体现除结构功能破坏外道路网络瘫痪的情况.故在将道路网络转化为网络体系中的网络时，需以道路实际运行阻抗并根据实际情况设置最大约束作为其联系的表达方式，使其能与其他网络相耦合，贴近实际情况.交通需求网络根源在于人的意念，而实际成行又受到现实条件约束，因此仅分析人的需求是无法体现出交通需求网络的真实变化.在将交通需求网络转化为网络体系中的网络时，需将需求传化为节点通行承载力剩余并设置约束.

在形成的网络体系中，并不是任何2个有依存关系的网络的所有节点都有依存.只有任意网络的节点失效后另一网络的对应节点因此受到影响而可能失效，才认为两网络的这一对对应节点相互依存，如某一节点道路阻抗较低且通行能力承载力剩余较多，交通管理措施施加影响也并不会造成其道路网络与交通需求网络的崩溃，则网络之间此节点是不相互依存的.

在交通系统受到异常影响时，交通需求网络与交通管理网络等之间并不存在直接性的影响，交通管理随着交通需求变化的调整有一定的滞后性，而交通需求网络与交通管理网络等的变化会直接影响道路交通网络，道路交通网络的变化也会影响其他网络的变化.因而交通系统的网络体系应是围绕道路交通网络的星形网络体系结构.在星形网络结构中，中心网络会对周边网络产生影响，见图1.

图1 交通系统网络体系构成

2 星形网络体系鲁棒性分析

假定星形网络体系中任意两网络A，B具有耦合作用，且服从度分布 PA（s，t），PB（s，t）.其中：s为单边联系；t为三角联系；x，y为参数.则整体度分布可通过下式得到.

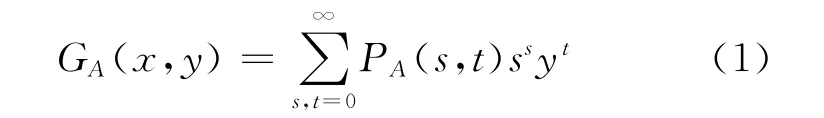
在开始受到异常影响时，网络体系中某一网络A有（1－p）比例的节点失效，可得到A网络变化的一般方程，即

考虑网络A与任意具有依存关系的网络B，假设CA比例的网络A节点是依存于网络B的且有CB比例的网络B节点是依存于网络A的，即意味假设这些节点失效会引起依存网络的节点失效，反之亦然.在不考虑反馈作用的情况下，经过n次级联失效，网络A与B在最大互联子团的节点比例分别为和∅n.直到网络A与网络B皆达到稳定态后，最大互联子团规模可以通过下式得到：

而影响之后属于剩余网络最大互联子团的节点比例gA（p），gB（p）可由下式计算得出.

以网络A为例分析.其中：u，v通过下式确定

同理可求得网络B的最大互联子团节点比例.

对于有q个网络的星形网络体系，都会有1个中心网络和（q－1）个其他网络.如果中心网络受到异常影响，那么这种破坏会传播到其他网络中然后再反馈影响到中心网络，网络渗流从一阶边为二阶.进一步简化假设中心网络依存节点Cr与相依的其他网络依存节点Co情况相似，即，可通过下式得到多次作用后的x，y参数取值.

同时，星形网络体系的鲁棒性与网络体系中网络个数具有相关关系，网络数越多其鲁棒性越差.在给定网络数量的网络体系中，其构成网络的聚类系数越高鲁棒性越差.

提高 星 形 网 络鲁棒性 的 方 法 有 3 种［14－15］：（1）增加网络中自治节点的比例，设定度较高的节点为自治；（2）使中心网络与其他网络的依存节点尽量相通，避免反馈失效；（3）中心网络节点保护系数加大.

3 算例分析

选取重庆市南岸区南坪组团片区路网为分析对象，路网结构见图2.

在实际分析为简化计算，以交叉口为道路网络、交通需求网络及交通管理网络的节点.其中交通需求通过将OD数据以就近原则加载于小区相邻的交叉口上并按照径路通行承载力计算通行承载力剩余.交通管理网络主要考虑交通控制对交通运行产生的延误，组织和诱导而产生的交通运行变化暂不考虑.

通过对随机异常影响，设定1～p程度的节点比例失效，直至网络稳定后完全瘫痪.最大互联子网规模变化见图3.

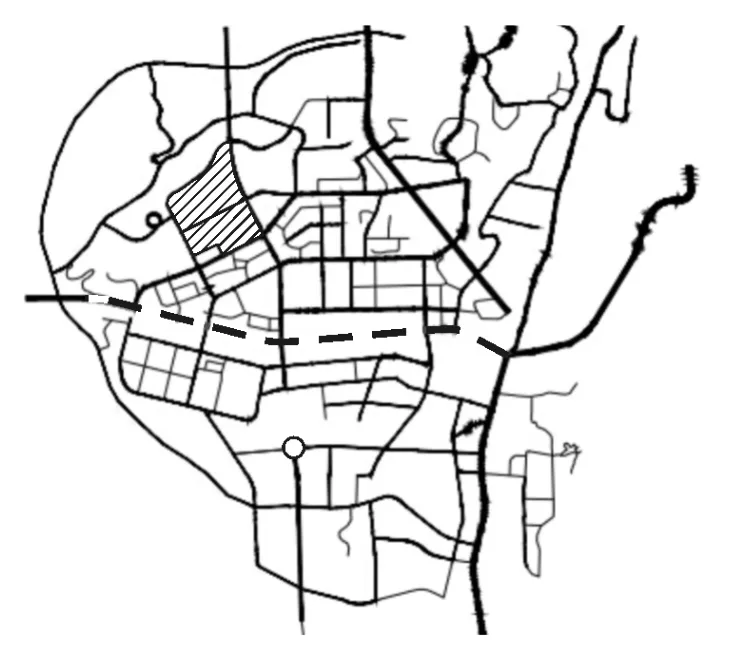
图2 示例路网结构图

图3 随机异常影响下交通系统分析结果

进一步，根据重庆市南岸区路网历史运行记录数据，选择现实发生过的道路失效，商业区开业及交通信号灯故障的交通运行异常事件，对应图2中虚线段、阴影部分及圆圈部分.将3次事件视为对道路网络、交通需求网络及交通管理网络的蓄意影响，将所涉及节点失效与现实路网运行状态进行对比分析.现实路网运行以路段服务水平以及交叉口服务水平为衡量，假设分析时段的交通需求不变化，当服务水平降至D以下时，视为节点或边失效.

4 结束语

文中以交通系统的脆弱性分析为分析对象，考虑交通系统的脆弱性受到多因素的影响，而这些影响因素既有独立性又存在相互依存关系，利用复杂网络理论中多网络体系鲁棒性分析方法，构建以道路网络、交通需求网络及交通管理网络等的星形网络体系.针对星形网络体系的特征，进行了算例分析，并结合交通运行历史数据，进行了对比研究.得出以网络体系研究城市交通系统受异常影响后的状态具有可行性.

表1 对比分析结果%

文中以图为城市交通系统的整体脆弱性分析提供新的研究思路，但在研究过程中存在较多不足，期望在未来的研究中继续深入.研究中存在如下几个问题：（1）道路网络、交通需求网络及交通管理网络各自具有不同的复杂网络特性，但在本文所采用的星形网络鲁棒性分析中对该特性做出了简化；（2）复杂网络体系的鲁棒性分析尚未形成理论体系，应用有较多限制；（3）对交通系统的宏观分析需要大量的基础数据，脆弱性分析的动态时变性要求与交通需求、交通管理等数据搜集速度存在矛盾.

［1］重庆市规划局.重庆市主城区交通运行分析年度报告［R］.重庆：重庆市交通规划研究院，2013.

［2］BERDICA K.An introduction to road vulnerability：What has been done，is done and should be done［J］.Transport Policy，2002（9）：117－127.

［3］SCOTT D M，NOVAK D.C，AULTMAN－HALL L，et al.Network robustness index：A new method for identifying critical links and evaluating the performance of transportation networks［J］.Journal of Transport Geography，2006（14）：215－227.

［4］JENELIUS E，PETERSEN T，MATTSSON L G.Importance and exposure in road network vulnerability analysis［J］.Transportation Research Part A，2006（40）：537－560.

［5］ABDUL A S M，AMIUL S A M.The completeness and vulnerability of road network in Bangladesh［J］.Engineering Concern of Flood，2013，5：201－208.

［6］张 勇，屠宁雯，姚林泉.城市道路交通网络脆弱性辨识方法［J］.中国公路学报，2013，26（4）：154－161.

［7］GAO Z Y，ZHAO X M，HUANG H J，et al.Research on problems related to complex networks and urban traffic systems［J］.J Tran Sys Eng ＆ Info Tech，2006，6（3）：41－47.

［8］GAO J X，BULDYREV S V，HAVLIN S，et al.Robustness of a tree－like network of interdependent networks［DB／OL］／［2011－08－30］.http：／／arxiv.org／abs／1108.5515.

［9］GAO J X，BULDYREV S V，HAVLIN S，et al.Robustness of a network of networks［J］.Phys Rev Lett，2011，107：195－201.

［10］UM J，MINNHAGEN P，KIM B J.Synchronization in interdependent networks［J］.Chaos，2011（21）：25－36.

［11］杨 超，涂颖菲，陈小鸿.交通网络需求脆弱性分析及应用［J］.同济大学学报：自然科学版，2012，9（40）：1329－1332.

［12］PARSHANI R，ROZENBLAT C.Inter－similarity between coupled networks［J］.Europhys Lett，2010，92：68002－68006.

［13］GU C G，ZOU S R，XU X L，et al.Onset of cooperation between layered networks［J］.Phys Rev E，2011，84：261－270.

［14］PARSHNI R，BULDYREV S V，HAVIN S.Interdependent networks：reducing the coupling strength leads to a cha nge from a first to second order percolation transition［J］.Phys Rev Lett，2010，105：248－271.

［15］BUIDYREV S V，SHERE N W，CWILICH G A.Interdependent networks with identical degree of mutually dependent nodes［J］.Phys.Rev.E，2011，83：106－112.