基于AIS信息的船舶航迹带尺度确定与分析
周 翠 肖进丽 牟军敏
(武汉理工大学航运学院1) 湖北省内河航运技术重点实验室2) 武汉 430063)
0 引 言
航迹带尺度是港口和航道规划、设计及建设的一个重要参数[1],现阶段国内外对船舶航迹带尺度的研究,主要有实船试验、模拟研究、理论计算等方法[2].但实船试验方法所要求的实验条件较高、风险大、成本高,且无法测得船舶在不同风、流(大小、方向)组合条件下的各种数据;理论计算方法难以全面考虑各种因素,且一些因素难以量化;而船模试验方法对一些量(风、流、拖船增减)的设定可能与实际情况存在着较大的出入.船舶自动识别系统(automatic identification system,AIS)是一种已得到广泛应用助航设备,该系统不仅能自动接收处理来自他船的操纵和船位信息,对他船进行识别、检测和跟踪,而且可在无人介入的情况下,主动地向合适的岸台、其他船舶或航空器提供实时连续、详细完整的航行状态信息和其他与安全有关的信息[3].利用船舶AIS所记录的实时反映船舶动态的航行信息(船长、船宽、船首向、航迹向、航迹点的经纬度等)计算船舶航迹带尺度可有效解决其他方法成本高、难量化、推广性低等问题[4].目前国内外对船舶航迹带尺度的确定主要依赖相关规范和标准[5-6],基于航迹带尺度的研究尚不多见,且大多以船舶模拟器试验为基础[7-8].已有一些学者利用 AIS数据对船舶航迹带尺度进行研究,陆吉庆[9]通过采集港口水域船舶AIS数据,利用回归分析方法确定了大型船舶航迹带宽度、转弯半径与船长、船宽、载重吨、吃水、风流等因素的关系;曾昆[10]利用AIS数据对厦门港附近大型船舶航迹带度、转弯半径进行了统计分析,但其都未利用AIS数据对航迹带尺度进行定量计算.
本文基于实船观测的AIS数据,拟合出所选取直线与转弯船舶航迹段的方程,运用船舶航迹带尺度模型,计算出航迹带的主要尺度(航迹带宽度和转弯半径),推算出船舶的漂移系数n的取值范围,并通过将计算所得结果与现行的《海港总体设计规范规范》(JTS 165-2013)(以下简称《规范》)中的规定进行对比分析以判别其可行性.
1 航迹带尺度模型
1.1 基于AIS航迹带宽度模型的建立
船舶航迹带宽度为船舶在航道内航行时,由于受到航道断面、导助航设施、外界自然条件和人为因素的影响,为了保证航向其航行轨迹在航道中线左右摆动,呈蛇形前进所占用的宽度.航迹带宽度由2个部分组成,船舶航行中在航迹线左右的偏移量;船舶本身占用的航道空间.
1.1.1 航迹偏移量
船舶航迹偏移量为船舶在航迹线附近蛇形前进所占用的空间.通过确定船舶航行时的航迹线,求出船舶航迹点在航迹线两侧的最大偏距之和,即得到船舶航迹偏移量.本文利用船舶AIS数据拟合出直线航段航迹线方程,利用点到直线的距离公式求得每个船位点至拟合直线的距离Dpi,找到拟合直线两侧各点至直线的最大距离和D-pmax,相加即可得出航迹偏移量A1,即

图1为船舶航迹线拟合示意图.图1中,黑色曲线为船舶航迹点组成的航迹线,黑色直线为拟合的航迹线.

图1 船舶航迹线拟合示意图
1.1.2 船舶本身占用空间
船舶本身占用空间,为船舶在航行过程某一刻所扫过水域范围的大小,它可以理解为船舶在航迹线法线上的投影,图2船舶所占空间示意图.

图2 船舶占用空间示意图
其中:M,N分别为船首、船尾的最外缘点;O为AIS设备在船上的安装位置;d1,d2分别为某观测时刻船首、船尾最外缘点M,N至航迹向的距离;L1,L2分别为船首和船尾至船载AIS设备O的距离;L和B为船舶的长度和宽度;γ为船舶航行当时的风流压差角.由图2可得:

1.1.3 船舶漂移系数
如上文所述,船舶航迹带宽度A为船舶航迹偏移量A1和船舶本身航行时占用空间A2之和,根据《规范》船舶航道的航迹带宽度A的经验公式为

式中:n定义为漂移系数;L为船长;B为船宽;γ为船舶航行时的风流偏压角.结合式(5),(6)可推导出:

综上,利用观测船舶记录的AIS数据(航迹向COG、船首向HDG、船长及船宽;其中风流偏压角γ可由船首向和航迹向的差值得到),即可计算出船舶航行航迹带宽度和漂移系数.
1.2 转弯半径模型
船舶AIS可每2s更新一次船舶实时船位信息(经纬度),通过转弯航段船舶的经纬度点,利用最小二乘法拟合曲线即可求得船舶的转弯半径.最小二乘法是通过最小化误差平方和的方式来寻找数据的最佳匹配函数.利用最小二乘法拟合圆的半径和圆心坐标的方法如下.
设样本点为(Xi,Yi),i∈(1,2,…),拟合圆心与半径为(A,B)和R,点(Xi,Yi)到圆心的距离为di:

点(Xi,Yi)到圆边缘距离的平方与半径平方之差为

Q(a,b,c)分别对a,b,c求偏导,令偏导等于0,得

按照上述原理进行C语言编程,将所选择的航迹点输入到程序,运行即可得到所选航迹点的拟合圆半径及圆心坐标.
2 基于AIS信息确定航迹带尺度实例
2.1 基于AIS数据的船舶航迹点绘制
本文所需的实测船舶AIS数据有:(1)动态数据:船舶位置(经度、纬度)、航迹向COG、船艏向HDG;(2)静态数据:船长、船宽.表1为本研究实测船舶的基本信息;表2为实测船舶AIS记录的经纬度转换后的坐标.

表1 实测船舶基本信息

表2 实测船舶AIS记录的经纬度转换后的坐标
将表2转换后的AIS经纬度坐标导入到SPSS中,得到该船舶在航道内的航迹线,见图3.

图3 实测船舶航迹线(SPSS)
2.2 航迹带尺度的确定
2.2.1 航迹带宽度
1)航迹线回归方程 截取09:58:00到10:00:30时间段实测船舶AIS记录的航迹点经纬度,运用SPSS软件对其进行线性拟合,见图4,拟合直线系数见表3.

图4 直线航迹线拟合

表3 回归系数
根据表3,该区段航迹线回归方程可表示为

2)回归方程检验结果 为验证航迹回归方程的可靠性,对其进行可信度检验.拟合方程相关系数检验、F检验、t检验的结果见表4.

表4 相关系数、F、t检验结果汇总
由表4可知,相关系数r=0.997,表明两变量线性相关程度极高;拟合方程常数与变量系数t检验与F检验的显著性概率Sig.都为0<0.05,表明回归效果显著,下面即利用该拟合结果计算观测船舶的航迹偏移量.
3)船舶航迹带宽度及船舶漂移系数的确定航迹偏移量A1为拟合直线两侧航迹点至该直线最大的距离和最小距离之和,利用点到直线的距离公式,求出各航迹点到拟合航迹线的距离.设直线外一点 P(x0,y0),直线l:Ax+By+C=0,AB≠0,则点到直线距离d=,各点至拟合直线距离如图5所示.由图5可得,点到直线的最大正距离为+2.940m,最大负距离为-3.289m,因此该航段的船舶偏移量A1为6.229m.
船舶本身占用空间宽度A2为船舶在航行过程的某一刻,船舶所扫过水域范围的大小,参照表3船舶基本信息可得A2≈10.335m.
由式(5)和(7)可分别计算出船舶航迹带宽度A=16.564m及船舶漂移系数n≈1.601.
随机选取其他4段直线航段,重复上述步骤,分别计算出航迹带宽度及漂移系数,结果见表5.

图5 点到拟合直线距离
表5结果显示,在该时间段观测船舶的航迹带宽度的范围为16.298~18.057m,漂移系数n的范围为1.575~1.745.

表5 不同航迹段的航迹带宽度及漂移系数
2.2.2 转弯半径的确定
截取10:38:40到10:48:40时间段船舶 AIS记录船舶航迹点的经纬度,将这些点导入到CAD中,运用最小二乘法编程对这些点进行拟合,圆心坐标(a,b)及半径r如下.

将拟合圆心和半径输入到CAD中,如图6所示;按照上述相同的步骤可计算出了该实测船舶航迹线及转弯段的转弯半径,将实测船舶航迹线直线段与转弯段所计算出的拟合方程相结合,可得到该实测船舶的完整航迹带尺度,见图7.

图6 转弯航迹线拟合图
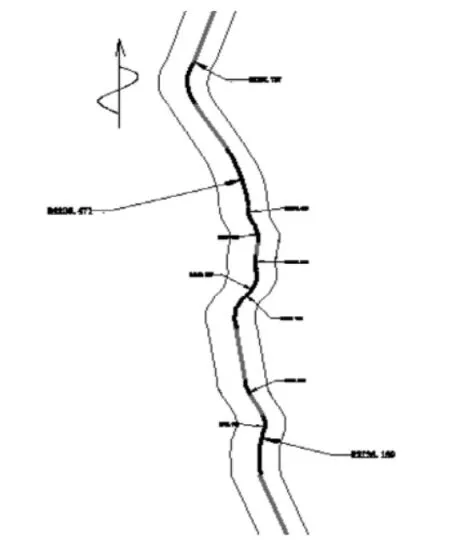
图7 实测船舶航迹带尺度
3 结果对比分析
3.1 航迹带宽度对比分析
《规范》中给出了满载船舶漂移系数n与风、流偏压角γ的经验值,见表6.

表6 满载船舶漂移系数n和风、流压偏角γ的关系
在航行条件流速V=0.5m/s,风流偏压角γ=7°的情况下,利用AIS数据计算所得的漂移系数范围为1.575~1.745,在同等条件下《规范》所规定漂移系数n=1.69上下波动,但整体上偏小,其原因在于实测的风流偏压角γ较7°大.
3.2 转弯半径对比分析
《规范》认为航道转弯半径的大小,应根据转向角φ和设计船长L 确定:当10°<φ<30°,r=(3~5)L;当φ>30°,r=(5~10)L.利用实测船舶AIS数据计算所得的船舶航迹带转弯半径,r=788.747m,船舶的船长L=44.8m,即

与《规范》中所规定的航道转弯半径r(最大为10L)相比,本文计算出的船舶航迹带弯曲半径较为偏大.究其原因,主要是本文用于AIS数据分析的观测船舶并非航行于该航道的最大代表船型,而对于船舶航行来说,航道弯曲半径越小航行越困难,因此,《规范》中所规定的航道转弯半径对于本文所使用的观测船舶安全过弯来说,其值有一定富裕.
4 结束语
本文利用实测船舶AIS数据,通过对船舶航迹带进行回归分析确定了航迹带宽度、转弯半径及船舶漂移系数的取值范围.所得结果与《规范》中相关规定对比分析,表明该方法是可行的.在利用船舶AIS数据对船舶航迹带尺度进行研究的过程中,存在一些不足与局限,如所采集的实测船舶的AIS数据有限,只计算出一条船舶在流速V=0.5m/s航行条件下的航迹带宽度和转弯半径,若能得到不同船型不同风、流下的观测船舶的AIS数据,所得结果将会更具代表性,且更有价值;在计算航迹带宽度时,利用不同数量的航迹点拟合直线方程,所计算出的航迹带宽度和船舶漂移系数存在一定差异,下一步研究将致力于发掘航迹点数与航迹带宽度及漂移系数之间的规律.
[1]于家根.港口水域航道合理规划设计研究[D].大连:大连海事大学,2008.
[2]陈 伟.大型集装箱船进出港行道宽度模拟实验研究[D].武汉:武汉理工大学,2010.
[3]刘 畅.船舶自动识别系统(AIS)关键技术研究[D].大连:大连海事大学,2013.
[4]PHILIPP L,CHRISTIAN B,MARTIN H,et al.Comprehensive analysis of automatic identification system (AIS)data in regard to vessel movement prediction[J].Journal of Navigation,2014,67(5):791-809.
[5]中华人民共和国交通部.JTS 165-2013海港总体设计规范[S].北京:标准出版社,2013.
[6]中华人民共和国交通部.GB50139-2004内河通航标准 [S].北京:标准出版社,2004.
[7]徐言民,荣祥斌,刘明俊.失控船拖带系统建模与航迹带模拟研究[J].中国航海,2008,31(2):126-129.
[8]索永峰,杨神化,陈国权,等.基于AIS航海模拟器目标船服务器的设计与实现[J].中国航海,2014,37(1):43-47.
[9]陆吉庆.港口水域航迹宽度和操纵参数的回归分析[D].大连:大连海事大学,2010.
[10]曾 昆.基于实态的船舶航迹带宽度和操纵参数的研究[D].辽宁:大连海事大学,2009.

