多类型动态广义出行费用随机用户平衡模型*
李小静 刘林忠
(兰州交通大学交通运输学院 兰州 730070)
0 引 言
城市交通网络上的路段和路径的通行能力因各随机因素影响不会永久保持它们的设计容量值,而是时刻处于一个随机的、动态的环境中并造成不同程度的下降,最终会导致城市整体或局部交通网络的通行能力随机动态降级变化.随机因素除了影响路网通行能力外,也会使得交通的OD需求量发生变化.在这样的供需不确定环境下,随着人们时间价值观念的加强,行程时间可靠性已经成为人们出行中第一或第二位要考虑的因素[1].Lam[2]经过调查计算得到行程时间可靠性的价值要明显高于行程时间的价值.实际出行中,人们不仅希望减少行程时间,而且更期待提高行程时间可靠性.除了这2个因素外,货币费用在某些情况下也是一个需要考虑的因素.这3个因素是影响出行者选择路径最重要的因素[3].但是目前的研究多以行程时间及其可靠性为主建立综合指标[4],而且指标多以静态来描述,从动态角度研究的比较少见.
为了更真实的体现出行者在随机路网上的出行行为,建立行程时间、行程时间可靠性和货币费用的广义出行费用指标,并将之动态化,提出“动态广义出行费用”,建立随机用户平衡模型.并根据出行者对路况熟悉程度划分为多个类型,在不确定条件下研究多类型出行者的路径选择行为.
1 符号定义及时间分布
1.1 符号定义
文中的常用符号定义如下.
N,A为交通网络中节点集合和路段集合,路段a∈A;W 为OD对集合,OD对ω∈W;Kω为OD对ω间所有路径集合,路径k∈Kω;xa,Ca,¯ca为路段a上的交通流量、实际通行能力和设计通行能力,ηa为路段a通行能力最大降级系数和实际降级系数,0<¯ηa≤1,ηa≥,Ta为路段a的自由流行程时间和实际行程时间为路段a的行程时间均值和标准差;为OD对ω间路径k上实际行程时间为路段路径关联系数,如果路段a在路径k上,其值为1,否则为0;为OD对ω间路径k上的路径行程时间均值和标准差;I为不同出行者类型的集合;i为第i类出行者,i∈I.
1.2 时间分布
受交通供需随机变化影响,路段和路径的行程时间均是随机变量,下面介绍它们的分布特征.
路段实际行程时间采用BPR函数,即

式中:β和n为定值,一般β=0.15,n=4.
假设随机变量Ca服从平均分布,其上、下界为和,即Ca~U),并进一步假定各路段容量相互独立,根据文献[5]可得到行程时间均值和标准差的计算公式为

根据假设可知各路段行程时间也是相互独立的,故路径行程时间计算公式为
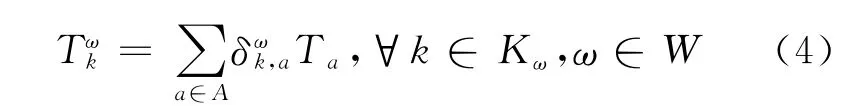
由概率论中心极限定理,路径行程时间服从正态分布,可以表示为

2 动态广义出行费用
2.1 动态指标
1)动态行程时间 式(1)可转变为

根据对随机路网的熟悉程度,将出行者分为多类,第i类出行者的行程时间可表示为

由式(9)可知,xai越大,行程时间越大;ηa越大即实际通行能力越大时,行程时间越小.故路段行程时间随路段上的实际流量以及实际降级系数变化而变化.
2)动态行程时间可靠性 Asakura等[6]定义行程时间可靠性为出行者能够在规定的时间内顺利到达目的地的概率.故路段、路径行程时间可靠性R一般表示为
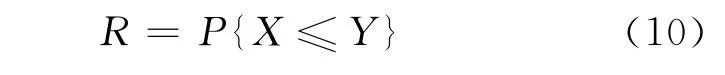
式中:P为概率计算;X为实际行程时间;Y为规定的时间阈值.
假设路段、路径行程时间均服从正态分布,则第i类出行者的行程时间可靠性可以表示为

式中:Φ(·)为标准正态分布;Yi为第i类出行者规定的时间阈值;μXi和σXi分别为第i类出行者路段或路径的行程时间的均值和标准差.因均值和标准差均受到流量的影响,故此时的行程时间可靠性是因流量而动态变化的函数.
3)动态货币费用 货币费用也一个重要的出行指标,文中基于式(1)得到路段a的货币费用为

第i类出行者的动态货币费用可以表示为

2.2 动态广义出行费用
出行者希望行程时间越小越好,可靠性越高越好,货币费用越少越好.这3个目标的理想状态一般不能同时达到,可定义广义出行费用为3个指标的加权平均和.
第i类出行者在路段a上的广义出行费用mai可表示为
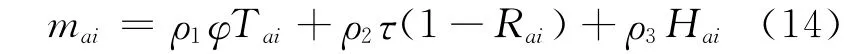
式中:Tai,Rai和分别为第i类出行者在路段a上的行程时间、行程时间可靠性和货币费用.φ为时间价值系数;τ为行程时间可靠性价值系数.ρ1,ρ2,ρ3为权重系数且和为1,可体现出行者不同风险偏好态度.
根据路径与路段的关系,第i类出行者在OD对ω间路径k的广义出行费用可以表示为
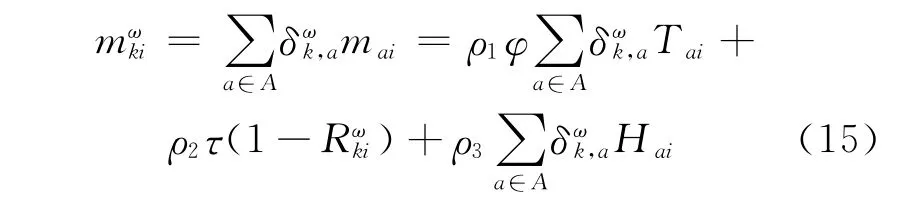
3 多类型动态广义出行费用随机用户平衡模型
3.1 模型的建立
出行者面对随机的实际路网,只能根据自己的偏好估计一个最小费用出行.本文假设出行者的路径选择标准是估计的最小动态广义出行费用,并且估计广义费用与实际广义费用之间有一个随机误差,各路径相互独立并服从甘贝尔分布.每类出行者以一定的概率选择路径,由离散理论OD对ω间的第i类出行者路径k被选择的概率为
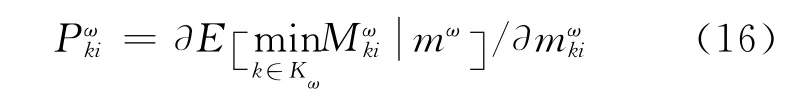

式中:θi为第i类出行者对路况的熟悉程度,该值越大表示出行者对路况越熟悉.
各类出行者在随机路网上的路径选择最后将达到Logit平衡状态,所有已选路径上的实际出行费用不一定相同,但必须满足以下平衡条件.
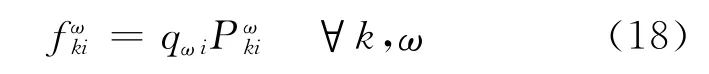
假设出行者交通需求是具有上限且与期望最小广义出行费用相关的严格单调递减函数,可表示为:


多类型出行者随机用户平衡问题可采用下面的数学规划模型.

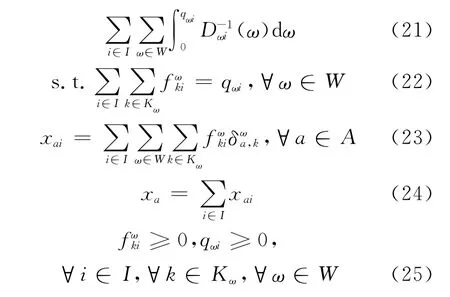
式(22)~(24)为交通量守恒条件;式(25)为交通量非负约束.
模型的等价性及惟一性证明可首先构造数学规划模型的拉格朗日函数,然后应用Kuhn-Tucker一阶最优性条件证明,具体证明过程可参考文献[7].
3.2 模型的求解算法
步骤1 初始化 根据初始零流求出各类出行者的路段广义出行费用 {=mai(0)},然后计算各类出行者的和.在路网G上随机分配各类出行者OD流量,得到路段初始可行流量 {},令迭代系数g=1.
步骤3 方向寻找 根据当前各类出行者的路径的广义出行费用 {},计算和.依次对在路网G上进行随机分配,得到各路段的附加交通流量}.
4 算例分析
4.1 测试网络
图1为一小型测试网络,包括一个OD对和3条路段.本文令τ=1.5,φ=1,ε=0.001.假设有2类出行者,OD流量为qωi=¯qωi-1.5Sωi,¯qωi=50 veh·min-1,i=1,2,2类出行者的出行量各占OD流量的50%.θ1=2,θ2=1,表明第一类出行者比第二类出行者对路况较熟悉.对路况熟悉的设置较小的时间阈值,不熟悉的设置较大的时间阈值:Y1=15min;Y2=30min.

图1 测试网络
各路段的属性见表1.以下如无特别说明,流量的单位均为veh·min-1,时间单位为min,费用单位为人民币.
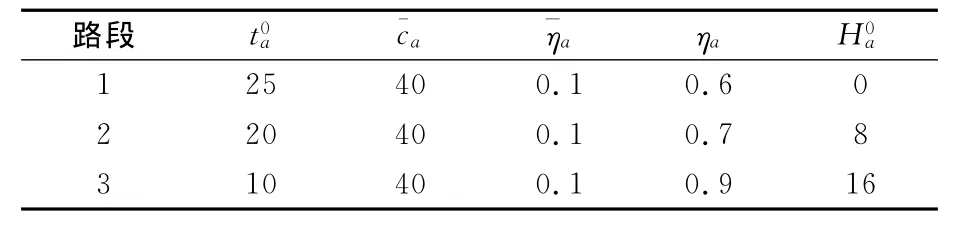
表1 路段属性
初始路网条件假定ρ1=0.3,ρ2=0.5,ρ3=0.2,可得到平衡配流结果.平衡时路段上的流量分别为:x11=0.334 7,x21=0.274 0,x31=19.747 7,x12=3.721 5,x22=3.367 3,x32=13.572 2.循环次数g=82,总需求qω=41.017 3.
从结果可知,在初始路网条件下,虽然路段3自由流货币费用最高,但两类出行者仍在路段3上分配了较大的流量.这主要是因为路段3的自由流行程时间较小,而且实际通行能力较大可靠性较高,因此路段3具有最低的广义出行费用.x31>x32,说明由于第一类出行者较熟悉路况,所以流量大于第二类出行者流量.
4.2 参数灵敏度分析
模型中θi体现不同类型出行者对路况的熟悉程度,指标权重可以体现出行者的不同的风险偏好和选择标准,规定的时间阈值对行程时间可靠性也有一定的影响.故下面将对这3个参数进行灵敏度分析,来验证出行者路径选择行为是否与经验相符.
1)路况熟悉程度影响 参数θ1和θ2取不同值时,计算结果见表2.
由表2可知,2类出行者都聚集在自由流时间较短的路段3上.随着θ1逐渐增大,x31逐渐增加;θ2逐渐增加时,x32逐渐增加;总需求越来越少.说明因为参数θ取值增大,出行者越来越熟悉路况,两类出行者都有更多机会选择到费用最少的路段3,从而导致OD对之间出行者的期望最小出行费用增加和OD需求量减少.
2)权重影响 指标权重取不同值时的平衡分配结果见表3.

表2 不同θ时的平衡分配结果

表3 不同权重时的平衡分配结果
由表3可知,当ρ1较大时,出行者以行程时间为主要选择依据.路段3的自由流行程时间最小,故x31和x32最大.ρ2较大时,出行者以行程时间可靠性为主要选择标准.第一类出行者在路段3上分配流量最大,路段1和2稍小,这是因为路段3降级后通行能力较大,可靠性较高.第二类出行者对路况不熟悉,综合考虑认为路段1和路段3的广义出行费用较低,故流量稍大.ρ3较大时,出行者主要以货币费用为路径选择标准.两类出行者分配结果类似,由于路段1自由流货币费用为0,故x11和x12最大;路段2、3由于费用较大,所以流量近似为0.不同权重分配结果与经验相符.
3)时间阈值影响 时间阈值取不同值时的平衡分配结果见表4.
由表4可知,当Y1增大时,第一类出行者在路段3上的流量向路段1、2少量转移.说明第一类出行者设定的阈值增大时,路段的可靠性均有所提高,这时会有少量的出行者放弃路段3而选择其他路段.当Y2减少时,第二类出行者在路段1、2的流量向路段3上少量转移.这是因为当阈值减少时,可靠性减少,出行者为了提高可靠性继续向路段3转移,使x32增大.该结论与实际相符合.

表4 不同阈值时的平衡分配结果
5 结束语
在降级路网和弹性需求下,采用行程时间、行程时间可靠性和货币费用的加权和定义了广义出行费用,并根据出行者对路网的熟悉程度划分为多种类型,建立了多类型出行者随机用户平衡模型,并用MSA算法求解,且算例结果分析均与经验相吻合.将规定的时间阈值考虑为流量的动态函数可作为下一步研究的方向.
[1]ABDEL-ATY M,KITAMURA R,JOVANIS P.Exploring route choice behavior using geographical information system-based alternative paths and hypothetical travel time information input[J].Transportation Research Record,1995,1493:74-80.
[2]LAM T.The effect of variability of travel time on route and time-of-day choice[D].Irvine:University of California,2000.
[3]WANG J Y T,EHRGOTT M,CHEN A.A bi-objective user equilibrium model of travel time reliability in a road network[J].Transportation Research Part B,2014,66:4-15.
[4]胡文君,周溪召.多用户多模式多准则随机用户均衡模型[J].武汉理工大学学报:交通科学与工程版,2012,36(2):366-370.
[5]LO H K,LUO X W,SIU B W Y.Degradable transport network:travel time budget of travelers with heterogeneous risk aversion[J].Transportation Research Part B,2006,40(9):792-806.
[6]ASAKURA Y,KASHIWADANI M.Road network reliability caused by daily fluctuation of traffic flow[C].Proceedings of the 19th PTRC Summer Annual Meeting,Brighton,1991:73-84.
[7]SHAO H,LAM W H K,TAM M L.A reliabilitybased stochastic traffic assignment model for network with multiple user classes under uncertainty in demand[J].Network and Spatial Economics,2006(6):173-204.

