出租车合乘定价多目标优化研究＊

张 薇 何瑞春 肖 强 马昌喜

（兰州交通大学交通运输学院 兰州 730070）

0 引 言

近年来，我国各大城市开始出现出租车合乘模式，出租车合乘指乘客经协商同意共同乘坐同一辆出租车的行为模式，能够在一定程度上提高运输效率［1］.国内外许多学者对合乘问题展开了研究，Lin等［2］基于费用的考虑研究了合乘路径优化方法；Yan等［3］基于拉格朗日松弛法建立了合乘路径规划模型；He等［4］基于GPS定位数据，采用数据挖掘技术研究了合乘路径的优化问题；Manzini等［5］设计了辅助合乘匹配的决策支持系统；肖强等［6］基于聚类和模式识别方法研究了合乘系统中的乘客匹配问题.目前的研究主要集中于合乘路径选择［7－8］及合乘匹配问题［9－10］，而较少涉及出租车合乘系统定价的优化问题，由于合乘系统价格参数直接关系到乘客、出租车司机及出租车公司等多方利益，所以合乘系统价格参数必须均衡考虑多方利益的最大化.文中综合考虑出租车合乘系统定价问题所涉及到的合乘支付比例、管理费、燃气补贴等多种价格参数，构建了多目标优化模型，设计了基于粒子群的多目标优化算法，通过计算分析了出租车与乘客供需比对优化结果的影响.

1 出租车合乘多目标优化模型

按照现行交通管理政策规定，合乘出租车时，合乘路段乘客只需支付一定比例费用（简称支付比例），独自乘车路段由个人承担费用.支付比例直接关系到司机与乘客双方利益.另外，出租车公司对司机收取的管理费、政府给予的燃气补贴也在一定程度上对司机的收入产生影响.因此，文中考虑支付比例、管理费及燃气补贴3个价格参数，以司机收入最大化、乘客支付最小化、出租车公司利益最大化、政府补贴最小化为目标，建立合乘系统的多目标优化模型.

令出租车合乘系统有N辆出租车，M位乘客，出租车的起步价为ps元／（akm），超过akm后，每车公里租价为pr元，行程为s的乘客独自乘坐出租车时的费用P（s）为

令乘客i的行程为si，yi＝1为乘客i以合乘模式乘坐出租车，yi＝0为乘客i独自乘坐出租车.若合乘时出现绕行现象，绕行方的费用按照原行程进行合乘优惠，不绕行方按照实际行程进行合乘优惠，zi＝1为乘客i合乘出租车并且为绕行方，否则zi＝0.dji＝1为车辆j拉载乘客i，dji＝0为车辆j未拉载乘客i，πi为乘客i合乘路段占其行程的比例；α为合乘支付比例.则乘客i的乘车费用为

计算车辆j的收入为

式中：β为每车每日需缴纳的管理费用，元／（本·d）；γ为每日的燃气补贴，元／d；W（lj）为车辆j当日行驶lj公里的燃气费用，按照每100km，8m3耗气量计算.

式中：q为每立方米燃气价格，元／m3；lj为车辆j当日行驶公里数，km.

出租车每车日均收入最大化为

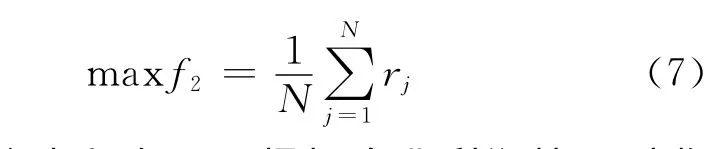
另外，令出租车公司根据企业利润情况对收取的车辆管理费的下限估算为βmin，司机对管理费的上限要求为βmax，政府根据财政支出情况对车辆燃气补贴的上限估算为γmax，考虑对每车实行相同的管理费及补贴，为了保证出租车企业与政府的利益，车辆需要交纳的管理费及获得的补贴需要在βmin＜β＜βmax，0＜γ＜γmax范围内，满足maxβ与minγ，将两者合并考虑为

综上，合乘系统的价格参数多目标优化模型如下.

2 算法设计

2.1 多目标适应度函数

合乘系统的价格参数包括支付比例α、管理费β、燃气补贴γ，因此定义粒子编码为（α，β，γ）.为区别多目标问题粒子的优劣性，粒子的适应度函数采取权重加权法，任意粒子xa的多目标适应度函数定义如下.

式中：fi，g为单目标fi的当前最优值；fi（xa）为粒子xa的单目标值；λi为各单目标的权重， ＝1.

2.2 非支配解集

多目标的Pareto解是不受其他解所支配的非支配解，建立非支配解集，将粒子中所有非支配解添加至非支配解集中，作为进一步选择全局最优与确定多目标Pareto解的基础.具体方法如下：对一粒子xa，如果不存在xb∈Ω，xb≠xa，使得对所有单目标fi（xb）≻fi（xa），i＝1，2，3，那么粒子xa为非支配解.

2.3 基于小生境的全局最优选择策略

根据小生境思想，随着进化相似粒子会逐渐聚集，从而形成若干小生境子群.本文以欧式距离表示粒子距离，并设计以下策略划分小生境子群：

定义1 粒子空间Ω中的任意2个粒子xa，xb∈Ω之间的距离D（xa，xb）用欧式距离表示为

定义2 Ω为粒子空间，X为Ω中的小生境子群集合，粒子xa∈Ω与小生境子群Xs∈X之间的距离D（xa，Xs）为

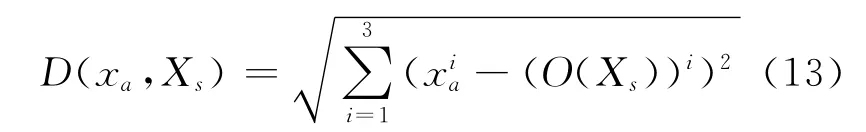
式中：（O（Xs））i为小生境子群Xs的中心点的第i个参数值，O（Xs）为小生境子群Xs的中心点.

定义3 小生境子群Xs的中心点定义为Xs中所有粒子的中心位置，当粒子xa加入小生境子群Xs时，Xs的中心点变换

定义4 若粒子xa∈Ω 满足：（1）min｛D（xa，Xk）｜Xk⊂X｝＝D（xa，Xs）；（2）D（xa，Xs）＜ε，则粒子xa与Xs为同一小生境子群；若只满足条件（1），则粒子xa单独作为一个小生境子群.其中：ε为所有粒子之间相互的平均距离.

基于以上定义将所有粒子划分为若干小生境子群，并进行全局最优粒子的选择，方法如下：根据多目标适应度函数在各小生境子群中选出最优粒子，作为最优粒子集，并计算各小生境子群的规模，即各小生境子群的粒子数，选出最优粒子集中所属小生境子群规模最小的粒子作为全局最优粒子.结合多目标适应度函数与小生境子群获得最优粒子的方法既能挑选出目标优化的粒子又能保留粒子的多样性.

2.4 粒子的更新

根据选择的全局最优更新粒子，粒子的速度和位置更新如下.

式中：w 为惯性权重；r1，r2为（0，1）之间均匀分布的 随 机 数；c1，c2为 学 习 因 子；分 别 是粒子xa在第t代时的速度和位置为粒子xa的局部最优位置为粒子群的全局最优位置.

2.5 算法流程

步骤1 随机生成乘客出行距离si～N（μ，σ2），以概率p1随机选择同意合乘的乘客yi＝1，根据出行距离配对合乘乘客，随机生成合乘路段比例πi∈ ［0，1］，以概率p2随机选择绕行的乘客zi＝1.对单独乘车的乘客i，若车辆j的当前行驶里程lj＜lmax，则分配dji＝1，对每组合乘乘客，若lj＜lmax，则将该组所有乘客分配给车辆j，至到所有乘客分配完或所有车辆的行驶里程达到最大值为止.

步骤2 初始化群体规模MP，最大迭代次数NP，惯性权重w等粒子更新参数，随机生成初始群体.

步骤3 按照非支配粒子选取方法，生成非支配解集.

步骤4 根据小生境子群划分方法，将非支配集中的粒子划分为若干小生境子群，并计算各小生境子群规模.

步骤5 计算粒子的多目标适应度函数，保留各小生境子群中适应度函数最优粒子，形成最优粒子集.

步骤6 选择规模最小的小生境子群中的最优粒子作为全局最优粒子.

步骤7 根据全局最优粒子更新粒子速度与位置，同时记录各粒子的个体最优.

步骤8 若迭代条件满足，算法结束，最优粒子集即最终Pareto解集，否则，转步骤3.

3 实例分析

假设出租车起步价10元／（3km），每车公里租价1.4元／车，单车日行驶最大里程200km，燃气价格3.10元／m3.设粒子群大小MP＝100，每日管理费βmin＝50元／d，βmax＝200元／d，每日燃气补贴γmax＝20元／d，出租车数量N＝100，乘客数量M＝2 500人，取目标权重λ1＝λ2＝λ3，惯性权重w＝0.3，学习因子c1＝c2＝2，乘客的出行距离si～N（8，4），乘客同意合乘的概率p1＝0.6，绕行概率p2＝0.1.基于本文提出的多目标优化模型与算法，得到迭代100次的优化结果见图1，图中看出，降低乘客支付的同时必然会降低车辆收入，燃气补贴的增加或者管理费的减少，能够提高车辆的收入，与实际相符.最优解具体见表1，解的分布均匀性较好，编号靠前的解，车辆收入水平较高，燃气补贴降低，收取的管理费较高；编号靠后的解乘客支付较少，但车辆收入较低；中间的解兼顾了各目标，在各目标之间找到均衡.根据结果分析，支付比例是合乘系统中的重要价格参数，过高或过低的支付比例都会直接造成其他目标变差，并且无法用其他价格参数弥补，本例的合适取值范围大约在［0.6，0.75］之间.

图1 M＝2 500人时的最优解集

表1 最优解集

为进一步分析最优解的价格参数对目标的影响，给出图2～3分别是乘客支付与车辆收入的影响关系图.图中显示乘客支付仅受到支付比例的影响，支付比例越大，乘客支付越多；而车辆收入同时受到支付比例、燃气补贴、管理费用的影响，当支付比例较高时，车辆收入较高，此时可以提高管理费或者降低燃气补贴，当支付比例较低时，车辆收入较低，此时需要降低管理费或者提高燃气补贴，以平衡司机、出租车企业各方利益.

图2 乘客支付的影响关系图

以上结果是在车辆数N＝100，乘客数M＝2 500人条件下得到的，下面考虑供需比对合乘系统价格参数最优解的影响.增大乘客数量，取乘客数M＝4 000，5 500人，得到的最优解集分别见图4～5.图中显示，当乘客数量达到4 000人时的最优解集明显朝着更加优化的方向移动，各目标都较乘客数量为2 500人时得到进一步优化.但是，当乘客数量继续增大到为5 500人时，最优解集基本上没有再发生变化，说明乘客数量已经超过了出租车的供给能力，出现了过剩乘客无法乘车的现象，所以此时各目标已经达到最优值，乘客数量的继续增加只会加重打车难问题.

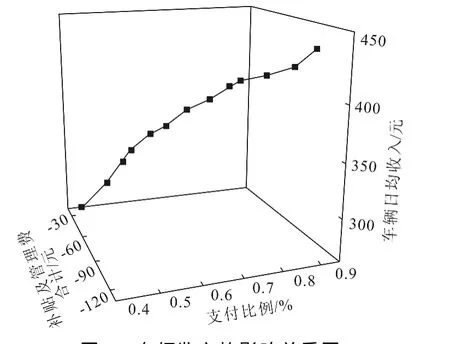
图3 车辆收入的影响关系图

图4 M＝4 000人时的最优解集

图5 M＝5 500人时的最优解集

4 结束语

文中研究了出租车合乘价格参数的最优解问题，得出以下结论：（1）当支付比例较高时，车辆收入及乘客支付均较高，此时可以提高管理费或者降低补贴，而当支付比例较低时，需要降低管理费或者提高补贴；（2）为了均衡系统各目标，必须选择合适的支付比例；（3）出租车与乘客的供需比对系统最优解有较大影响，随着乘客量的增加，各目标逐渐优化，直到供需比达到饱和时，系统各目标达到最优值，若供需比继续减小，只会造成更多的剩余乘客无法乘车的现象.文中工作能够解释出租车合乘系统的相关现象，所得结论对出租车政策的制定有一定的指导意义.

［1］ZHANG D，HE T，LIU Y H，et al.A carpooling recommendation system for taxicab services［J］.IEEE Transactions on Emerging Topics in Computing，2014，2（3）：254－266.

［2］LIN Y，LI W，QIU F，et al.Research on optimization of vehicle routing problem for ride－sharing taxi［J］.Procedia－Social and Behavioral Sciences，2012，43：494－502.

［3］YAN S Y，CHEN C Y，WU C C.Solution methods for the taxi pooling problem［J］.Transportation，2012，39（3）：723－748.

［4］HE W，HWANG K，LI D.Intelligent carpool routing for urban ridesharing by mining GPS trajectories［J］.IEEE Transactions on Intelligent Transportation Systems，2014，15（5）：2286－2296.

［5］ MANZINI A P.A decision－support system for the car pooling problem［J］.Journal of Transportation Technologies，2012，2（2）：85－101.

［6］肖 强，何瑞春，张 薇，等.基于模糊聚类和识别的出租车合乘算法研究［J］.交通运输系统工程与信息，2014，14（5）：119－125.

［7］CHUNG C L，JENG J Y，LEE Z Y.Study of carpool user behaviors and route characteristics in Taiwan［J］.Sustainable Transportation Systems，2012（5）：356－363.

［8］CHEN Y T，HSU C H.Improve the carpooling applications with using a social community based travel cost reduction mechanism［J］.International Journal of Social Science and Humanity，2013，3（2）：87－91.

［9］KAMMERDIENER T，ZHANG H.Classification of ride－sharing partners based on multiple constraints［J］.Journal of Computing Sciences in Colleges，2011，26（4）：95－101.

［10］GUO Y，GONCALVES G，HSU T.A clustering ant colony algorithm for the long－term car pooling problem［J］.International Journal of Swarm Intelligence Research，2012，3（2）：39－62.