通用型无参考图像质量评价算法综述
张淑芳,张 聪,张 涛,雷志春
ZHANG Shufang,ZHANG Cong,ZHANG Tao,LEI Zhichun
天津大学 电子信息工程学院,天津300072
School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China
1 引言
图像质量评价能有效评估图像采集和处理过程所引起的失真或退化,具有很好的理论价值和应用前景。目前研究较多地全参考(Full-Reference,FR)和部分参考(Reduced-Reference,RR)评价算法,由于要用到参考图像的先验信息,因此在实际应用中受到限制。无参考(No-Reference,NR)评价算法不依赖原始图像信息,具有实际的应用前景。
无参考图像质量评价算法按照其适用范围可分为专用型方法和通用型方法两种[1],如图1 所示。专用型无参考评价算法针对特定失真类型图像进行评价,如文献[2-5]提出了针对图像JPEG 压缩编码失真的评价算法,文献[2-3]通过测量块边缘强度及其他特征对图像进行评价,Zhou 等人提出了基于边缘平均误差和图像活跃性的特征学习方法[4];文献[6-10]是针对图像JPEG2000压缩编码的算法,该类算法通常采用边缘检测和建立边缘分布模型来衡量图像的振铃效应和模糊程度;文献[11-16]是针对图像模糊的评价算法,Caviedes 等人通过计算轮廓上图像块DCT 的峰度(Kurtosis)平均值反映图像模糊程度[11],Ferzli等人利用恰可察觉模糊(Just Notice Blur,JNB)的方法来评价图像质量[12],桑庆宾等人通过构造模糊副本来计算结构相似性[14]。实际应用中图像失真类型具有多样性和相互叠加性,因此,针对特定失真类型的无参考质量评价算法的应用受到严重限制。
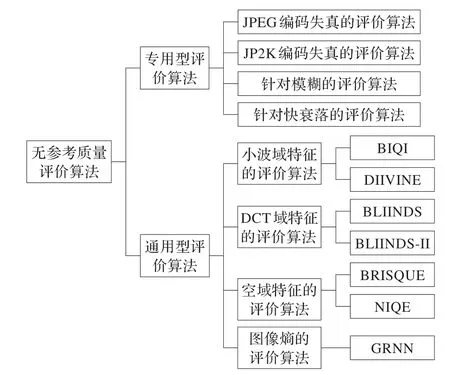
图1 无参考图像质量评价算法分类
当前通用型无参考图像质量评价算法是本领域的研究热点,Moorthy 等人于2010 年提出了一种基于两级框架的无参考图像质量评价模型(Blind Image Quality Index,BIQI)[17],在失真图像的小波域提取统计特征和利用支持向量机(Support Vector Machine,SVM)进行图像失真类型分类的基础上,融合专用型无参考质量评价方法,计算图像客观质量分数。Moorthy 等人在BIQI模型的基础上提出基于失真类型识别的图像真实性和完整性评价模型(Distortion Identification-based Image Verity and INtegrity Evaluation,DIIVINE)[18],利用可控金字塔[19]在方向和尺度上进行小波分解,提取归一化小波系数[20]统计特征,然后利用支持向量机建立特征模型。
有别于两级框架的无参考图像质量评价算法,以下几种评价方法不需要对图像进行失真类型分类。Saad等人提出了BLIINDS(BLind Image Integrity Notator using DCT Statistics)算法[21],并提出了BLIINDS-II改进算法[22],其通过在图像DCT域提取DCT系数的统计特征建立支持向量回归(Support Vector Regression,SVR)模型。Mitta等人提出了BRISQUE(Blind/Referenceless Image Spatia Quality Evaluator)算法[23],通过对图像的空域归一化[24系数提取统计特征建立回归模型。在BRISQUE 方法的基础上,Mittal 等人又提出了完全无参考算法NIQE(Natural Image Quality Evaluator)[25],该算法通过计算失真图像与无失真图像的多元高斯模型(Multivariate Gaussian Model,MVG)距离来衡量图像质量。Li 等人提出了基于广义高斯模型的GRNN(General Regression Neural Network)算法[26],通过提取图像的相位一致性模型熵、相位一致性模型均值、失真图像的梯度均值以及失真图像熵等特征,运用广义高斯模型进行特征建模。贾惠珍等人[27]为了弥补文献[23]统计特征的缺点,通过引入文献[26]中提出的相位一致性等视觉特性,有效提高了评价性能;李朝峰等人提出了利用灰度-梯度共生矩阵计算图像相位一致性模型熵的图像统计特征[28],以及结合NSS 和小波变换的无参考图像质量评价[29]。
本文将对几种典型的通用型无参考图像质量评价算法进行讨论,首先介绍通用型算法特征提取和质量评价的原理;然后在LIVE 数据库[30]上对上述评价方法进行仿真评估,并分析和比较了各种算法的评价性能和执行速度;最后对无参考图像质量评价算法的进一步研究方向做简要概括。
2 评价方法介绍
2.1 基于小波域特征的评价方法
2.1.1 BIQI算法
Moorthy 等人提出了一种基于小波域的自然图像统计特性算法(BIQI)[17],认为失真会影响图像小波域自然统计特性[31],并且这种影响是有规律且可量化的。BIQ算法提出两级框架的模型,第一步利用支持向量机(SVM)识别图像中存在每一种失真类型的可能性;第二步利用专用型无参考方法或者利用支持向量回归(SVR)计算图像在每一种单一失真类型下对应的图像质量;最后利用第一步得到的失真类型可能性对第二步的结果进行加权平均得到图像质量。
对于一幅输入图像,利用Daubechies 9/7 小波基,经过3 级尺度和3 个方向的小波变换之后得到子带系数,然后用一种广义高斯分布(Generalized Gaussian Distribution,GGD)进行拟合:


利用多分类支持向量机(Multiclass-SVM)对训练集中5 种失真图像提取上述的特征向量进行训练。SVM 预测出失真图像中存在每一种失真类型的可能性pi{i=1,2,…,5}。针对5 种失真类型,利用特征向量fi,分别进行SVR 训练得到特征向量与图像主观质量之间的映射关系qi{i=1,2,…,5}。然后计算图像的客观评价质量:
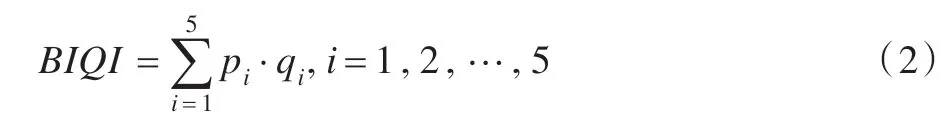
在进行SVM 分类时,采用的是径向基函数方法(Radial Basis Function,RBF),以5 重交叉验证的方式确定SVM 参数;采用v-SVM 进行回归训练,(C,γ,ν)参数采取与SVM 同样的交叉验证方式进行确定,其中ν取确定值0.5。
BIQI 算法测试图像质量时,由于在多尺度多方向小波变换子带上提取特征,并利用支持向量机进行回归预测,因此客观评价分数与主观评价分数之间的一致性较好。
2.1.2 DIIVINE 算法
Moorthy 等人在BIQI 算法基础上进行了改进,提出了基于失真类型识别的图像真实性和完整性评价算法(DIIVINE)[18],不同于BIQI 只提取一些简单的边际描述的特征,该算法提取了与视觉一致性的统计特征。文献[33]证明了图像的尺度空间方向分解小波变换与大脑初级视觉皮层的空间分解相对应。该算法对于分离归一化[20]的小波系数进行特征提取,并利用与BIQI相似的方法计算图像质量。
(1)小波系数归一化
该过程分两步进行:第一步,利用可控金字塔[33]在两级尺度、6 个方向执行小波分解。小波分解系数用表示,θ∈{0°,30°,60°,90°,120°,150°},α∈{1,2}。第二步,执行重要的视觉分离归一化变换(Divisive Normalization Transform)过程[19]。定义一个归一化邻域向量Y,其包含了15 个系数(9 个来自子带中间系数yc的3×3 邻域,1 个自来小波母带,5 个来自同一尺度上的相邻子带)。用高斯尺度混合(Gaussian Scale Mixture,GSM)模型[34]对Y建模。对于一个满足GSM 模型的N维随机向量Y,令Y≡z·U(≡表示概率分布相等),z是随机变量,U是零均值高斯随机向量(方差为CU),Y的概率密度可以表示为:
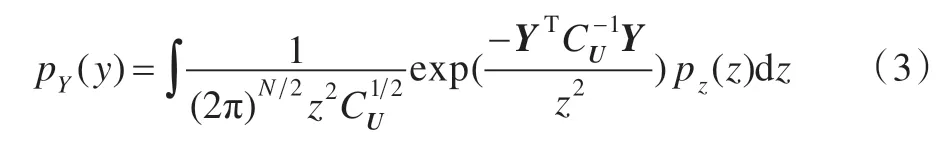
在已知向量Y的情况下,归一化参数p可以表示为:,分离归一化变换之后的系数,得到了分离归一化变换之后的子带系数。分离归一化过程使得自然图像的子带统计特性分布特征更接近于高斯分布。
(2)小波系数统计特征
小波系数统计特征包括:子带分布特征、方向相关性、尺度间相关性、空间自相关性和空间互相关性。
子带分布特征:12 个子带上的子带系数用公式(1)进行表示,由于μ=0,采用快速匹配法[35]估计分布参数(σ2,γ)作为子带分布特征。
尺度相关性特征:每一个带通(BP)子带用窗函数方法[10]比较其高通残余带。采用标准差σ=1.5 的15×15 高斯窗函数对BP 和HP 带进行滤波。结构相关性计算公式为:

σxy表示BP与HP窗口区域内协方差,分别是BP与HP 窗口区域方差,C2为一个常数,对子带内所有的局部区域相关性求平均值pˉ,将其作为尺度相关性特征。
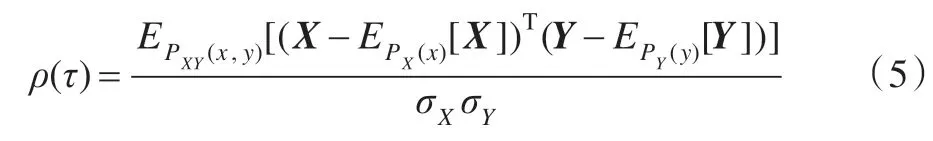
空间互相关性特征:将θ∈{0°,30°,60°,90°,120°,150°6 个方向的子带,分为组。采用与计算尺度相关性特征的窗函数方法[10],计算每组子带中的区域相关性,并取最低的5%的区域相关性数值,作为空间互相关性特征。
(3)计算图像质量
对提取的归一化小波系数统计特征,分别利用多分类支持向量机(SVM)和支持向量回归(SVR)进行失真类型分类和回归预测客观图像质量,具体方法与BIQI相似。
与BIQI 算法相比,DIIVINE 算法由于提取了全面、复杂的图像小波域统计特征,因此DIIVINE 算法与主观图像质量评价方法取得了更好的一致性。但是该算法需要进行小波变换,并且提取特征数量较多,机器学习的难度也比较大。
2.2 基于DCT 域特征的评价方法
2.2.1 BLIINDS 算法
由于自然图像具有高度结构化特性[24],人类视觉特性(Human Visual System,HVS)倾向于从视觉图像中提取结构信息,并且对图像的对比度高度敏感。Saad 等人提出了一种基于DCT 域统计特性的图像完整性评价方法(BLIINDS)[21]。BLIINDS 提取DCT 系数的统计特征,利用机器学习的方法来评价图像质量。
(1)DCT 域的特征提取
DCT 域的特征包括对比度特征、结构特征以及各向异性。
对比度特征:对比度是图像的一个基本视觉属性,将图像分为B×B的图像块进行二维DCT 变换,局部DCT 对比度定义为交流AC系数与直流DC系数幅值的平均。整幅图像的全局对比度为图像块局部对比度的均值,计算公式为:
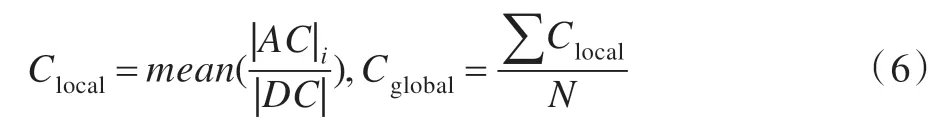
结构特征:DCT 域AC系数直方图统计特性,首先需要计算峰度(kurtosis),峰度是用来反映频数分布曲线顶端尖峭或扁平程度的指标,其计算公式为:k(x)=E(x-μ)4/σ4,μ表示x的均值,σ表示标准差。对最小的10%局部峰度kb计算均值,将其作为结构特征。
各项异性特征:按照{0°,45°,90°,135°}4 个方向将图像分为互不重叠的B×1 图像块,计算图像块的一维DCT 变换,用Pθ[n,k]代表图像块的DCT 变换AC系数,1 <k≤B代表该图像块DCT 系数序号,n代表该图像块在图像中的空间序号,θ表示方向。将图像块的DCT 变换系数进行归一化,利用归一化系数计算出图像块的雷尼(Renyi)熵:
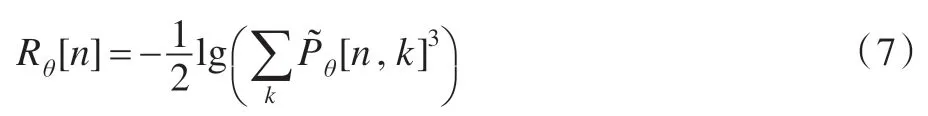
图像θ方向的平均雷尼熵用E(Rθ)表示,4个方向上平均雷尼熵方差为var(E[Rθ]),最大平均雷尼熵为max(E[Rθ])。提取var(E[Rθ])与max(E[Rθ])作为图像各向异性特征。
(2)图像质量计算
向量Xi={fi|i∈1,2,…,8}表示第i幅图像上提取的特征向量,DMOSi表示第i幅图像主观质量分数。算法用多元高斯分布(Multivariate Gaussian Distribution,MGD)模型或者多元拉普拉斯分布(Multivariate Lapla cian Distribution,MLD)模型对图像特征进行拟合,因为这两种模型仅仅需要估计均值和方差两个参数。通过在LIVE 数据中选取部分图像作为训练样本提取图像特征X,训练得到概率模型P(X,DMOS)。对于输入图像,提取特征向量Xi,计算maxP(DMOSi/Xi)即为图像质量。
BLIINDS 算法的模型训练不需要知道训练样本的失真类型,并且特征训练过程简单,算法复杂度低于基于两级框架的算法。
2.2.2 BLIINDS-II算法
BLIINDS-II算法[22]在BLIINDS 算法的基础上,对特征选取和特征拟合形式进行了一些改变,使得客观评价结果更符合主观评价。BLIINDS-II 在图像的DCT 域提取的特征包括:广义高斯分布(Generalized Gaussian Distribution,GGD)形状参数特征、频率变化系数、能量子带比例和方向特征等。
GGD 模型形状参数特征:与BLIINDS 算法一样,将图像分为B×B的图像块进行二维DCT 变换,用公式(1)广义高斯模型拟合DCT 的交流系数,(μ,σ2,γ)分别是该模型的参数。并将整幅图像中最小的10%个γ值求平均作为特征f1,对全部图像块的γ值求平均作为高斯形状参数特征。
频率变化系数特征:对图像中所有的块计算频率变化系数ζ=σ/μ,对最大的10%图像块和全部图像块求均值,记为Em[ζ]和E[ζ],将其作为频率变化系数特征。
能量子带比例特征:图像失真通常会使图像局部的光谱特征(Spectral Signatures)发生改变。局部DCT的能量子带比例能够反映图像失真。如图2(b)将DCT的AC系数分为3 个频率子带,令Ωn(n=1,2,3)代表从低到高的频率信息子带。定义子带n的平均能量为:,为广义高斯分布(1)的方差拟合参数,然后计算能量子带比例:
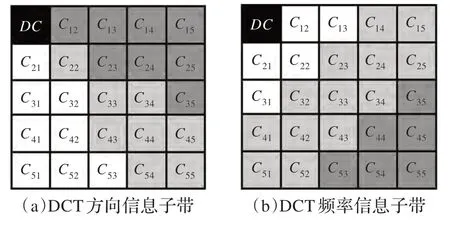
图2 DCT 系数的子带分区
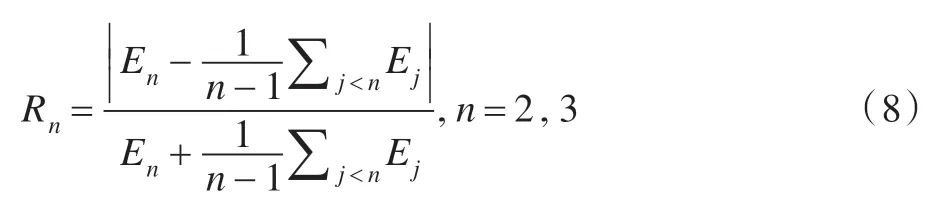
同样,对最大的10%图像块求均值和全部图像块求均值,记为Em[Rn]和E[Rn],作为频率变化系数特征。
方向特征:按照图2(a)的方式将图像块DCT 域的AC系数分为3 个方向信息子带。对每一个子带采用广义高斯模型进行拟合,得到模型参数ζn(n=1,2,3),然后计算每一个子带内ζn的方差var(ζ)。分别对最大的10%图像块求均值以及全部图像块求均值,记为Em[var(ζn)]和E[var(ζn)],将其作为方向特征。
BLIINDS-II 最后图像质量计算方法与BLIINDS 相同,BLIINDS-II 的贡献在于选取了DCT 域更加符合人眼视觉效应的特征,因此在图像质量评价性能上得到了很大提高。
2.3 基于空域特征的评价方法
由于空域的失真是影响图像视觉质量的直接原因,有效的空域特征提取可取得与主观评价较好的一致性。并且相比于变换域(小波域、DCT 域等)特征提取,空域特征提取算法具有复杂度低和执行速度快的优点,适合应用到实时系统。
2.3.1 BRISQUE 算法
Ruderman等[24]发现自然图像归一化的亮度值趋向于单元正态高斯特性,他认为图像中的失真会改变归一化系数的统计特征,通过测量这种统计特征的改变,可以预测失真类型并以此评价图像视觉质量。在此理论的基础上,Mittal 等人提出了基于空域统计特征的BRISQUE算法[23]。
(1)图像像素归一化
对于一幅图像,通过分离归一化[33](Divisive Normalization)的方法计算归一化亮度。假定亮度图像I(i,j),分离归一化计算公式为:
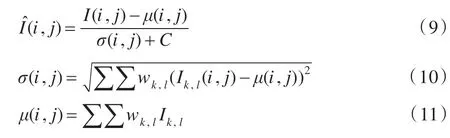
i∈1,2,…,M,j∈1,2,…,N是空域的系数,M、N分别是图像的高度和宽度,C是常数。其中,圆形对称的高斯权重函数w={wk,l|k=-3…3,l=-3,…3}。称归一化后的亮度值为MSCN(Mean Subtracted Contrast Normalized)系数。与I(i,j)相比,减少了相邻像素之间的相关性。
(2)空域特征提取
失真的存在会破坏相邻MSCN 系数之间存在的规律性。归一化系数的特征包括广义高斯分布特征和相邻系数相关性。
广义高斯分布特征:模型公式可表示为:
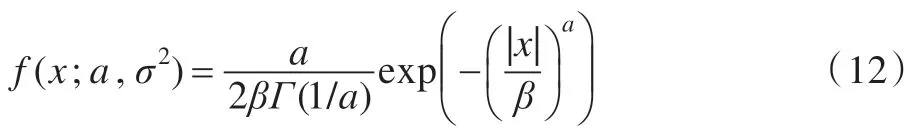
相邻系数相关性:从水平、垂直、主对角线和次对角线4 个方向得到相关性图像[34],采用非对称广义高斯分布(Asymmetric Generalized Gaussian Distribution,AGGD)[21进行拟合,每个方向的估计参数(η,v,σl,σr)利用快速匹配法[36]进行估计。4 个方向估计的16 个参数作为相邻系数相关性特征。
然而由于自然图像统计特性的多尺度性,作者通过实验发现在2个尺度下分别提取2个广义分布特征和16个相邻系数相关性特征较合理,故一共提取(2+16)×2=36个特征。
(3)图像质量计算
利用支持向量回归得到回归模型,训练出图像特征与主观图像质量分数之间的映射关系。对于待测图像,提取其特征向量代入到训练好的SVR 回归模型来计算图像质量。
2.3.2 NIQE 算法
NIQE 算法提取了与BRISQUE 类似的图像特征,但算法的主要贡献在于训练回归模型时,不再需要图像的主观评价分数,而是在原始图像库[37]上提取图像特征,然后利用多元高斯(MVG)模型进行建模。另一个贡献是,NIQE 算法基于人眼对图像中对比度较高区域更敏感的特征,提出在图像中选取显著区域建立特征模型的方法。
(1)显著区域图像子块图像特征选取
利用公式(10)中的局部方差σ(i,j)可以衡量图像局部锐度。将图像分为P×P尺寸的图像块,计算图像块b局部的平均方差:

δ表示局部图像块的平均方差,选取δ>T的图像块作为特征显著图像块,T通常取最大局部平均方差的0.6~0.9 倍。
在提取的图像显著块上,对归一化系数利用广义高斯分布模型(GGD)进行拟合,采用快速匹配法[35]估计归一化后的广义高斯分布参数(a,σ2)。然后再采用非对称高斯模型(AGGD)对4 个相邻系数乘积进行拟合,采用快速匹配法[36]得到16 个相邻系数参数。同样由于图像视觉特性是多尺度的,故本文在两个尺度下提取图像统计特征,一共具有(2+16)×2=36 个特征。
(2)图像质量计算
对提取的36 个特征,通过拟合多元高斯(MVG)模型计算模型参数v和Σ,v和Σ分别代表MVG 模型的均值和方差矩阵。MVG 模型公式为:
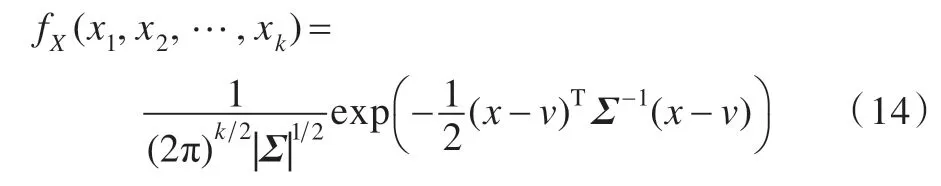
其中(x1,x2,…,xk)是提取的图像特征,v和Σ可利用最大似然估计方法[38]进行计算得到。
然后提取失真图像统计特征,进行MVG 模型拟合得到(v′,Σ′),计算失真图像与自然图像拟合参数之间的距离来衡量图像质量:
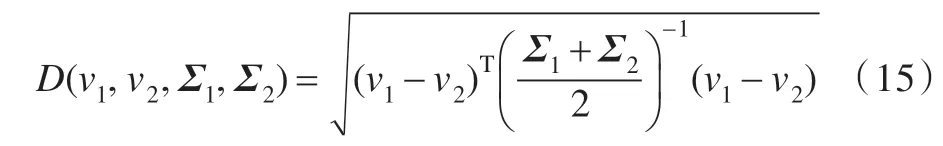
上式v1,v2,Σ1,Σ2分别代表自然图像与失真图像的MVG 模型均值和方差矩阵。
NIQE 算法的模型训练不依赖于任何主观评价分数,且图像质量计算的算法复杂度较低,因此可以应用到实时系统。
2.4 基于图像熵特征评价方法
图像熵可反映图像的边缘和纹理等细节,文献[39]利用图像熵识别图像的各向异性,文献[40]计算图像熵用于评价图像质量。利用相位一致性作为图像特征可很好地表示图像质量。图像中大量的视觉信息都存在于频域相位中,而非频域幅度[41-42]。梯度也是构成图像边缘或者轮廓的重要因素,梯度的变化反映图像细节、纹理的变化。Li 等人[26]利用相位一致性和图像梯度等图像特征,提出了一种基于广义神经网络的无参考图像质量评价算法(GRNN)。
(1)相位一致性计算
相位一致性的潜在规律是,图像中的重要视觉特征存在于其傅里叶分量(谐波分量)具有一致性的像素里[43]。相位一致性函数为信号I在x处的傅里叶系数展开[44]:

其中An表示I的第n次谐波分布的幅度,ϕ(x)表示x处谐波分量的局部相位,是x处的平均相位。公式(16)取得最大值对应的,记为PCI(x)。利用文献[43]或者文献[44]中的方法计算相位一致性。
(2)图像质量计算
首先计算图像的相位一致性图像,然后计算相位一致性图像均值、相位一致性图像熵、失真图像熵和失真图像梯度等4 个特征。GRNN 算法利用广义回归神经网络对特征参数进行拟合[45]。对于输入向量X,图像质量预测值,广义回归神经网络模型公式为:
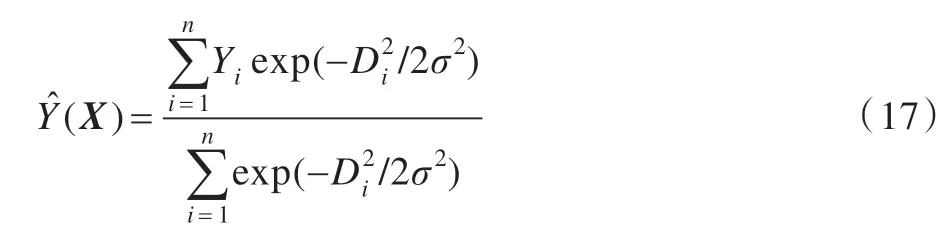
GRNN 算法是一种非机器学习的无参考图像质量评价算法,采用与人类视觉相关的图像一致性进行特征提取,并且该算法的计算复杂较低。
3 实验结果与分析
3.1 测试图像库的选取
用于图像质量评价算法性能测试的标准图像库主要有LIVE图像质量评价数据库[46]、TID2008[47]和TID2013[48等。TID2008 以及TID2013 数据库包含的图像多,且将图像失真类型分的更细,适合于全参考图像质量算法的性能评价。目前无参考质量评价算法主要将图像失真类型分为5 类,即JPEG、JP2K、白噪声(WN)、高斯模糊(Blur)和快衰落(FF)。LIVE 数据库中包含29 幅未失真图像以及与其对应的5 类失真图像,并且每一类失真图像有5 级失真程度,有利于评价无参考质量评价算法的性能。因此,本文选用LIVE 标准图像库进行算法性能评估。
3.2 评价指标
客观图像质量评价算法的性能评价主要测量客观评价数据与主观评价数据的一致性。视频质量专家组(Video Quality Experts Group,VQEG)[49]提出了4 种评价指标:斯皮尔曼等级次序相关系数(Spearman Rank Order Correlation Coefficient,SROCC)、肯德尔等级次序相关系数(Kendall Rank Order Correlation Coefficient,KROCC)、皮尔森线性相关系数(Pearson Linear Correla tion Coefficient,PLCC)和均方根误差RMSE。SROCC公式为:
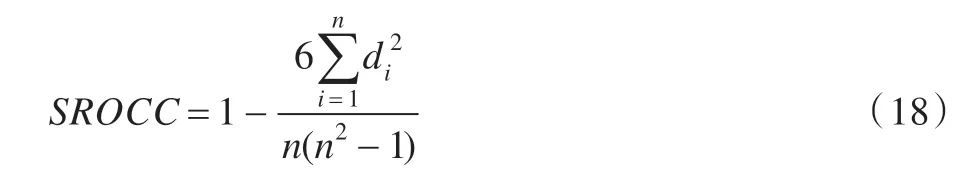
其中di表示第i图像在主观评价分数中的排序与客观评价分数中排序的差值。KROCC公式为:

式中,nc表示主观数据与客观数据一致的数据对的数目,nd表示不一致的数据对的数目。例如,对于任意的一对观测数据(xi,yi)和(xj,yj),如果同时满足xi>yi和xj>yj,或者满足xi<yi和xj<yj,则称该“数据对”是一致的。
对于PLCC的计算,首先要对主观数据与客观数据进行非线性拟合,文献[50]给出了一种Logistic 函数对数据进行拟合:
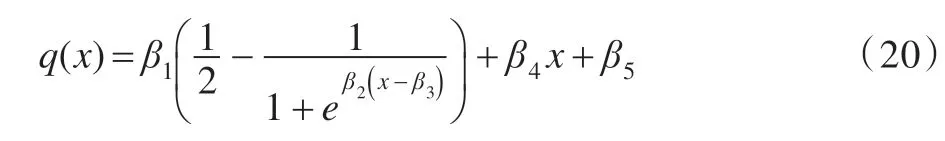
其中,βi是需要拟合的参数,本文借助于1stopt 优化软件进行参数拟合。PLCC计算公式为:
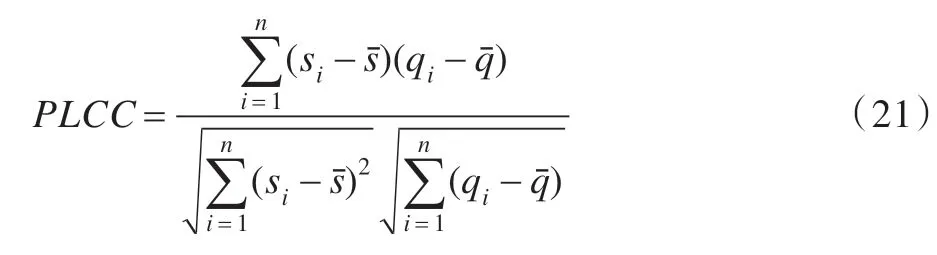

4 种评价指标中,SROCC与KROCC两个的评价都是计算数据对的一致性,故具有相似的结果;PLCC与RMSE在计算客观与主观数据一致性过程中,需要使用拟合算法得到拟合曲线,拟合曲线的优劣直接导致影响主客观数据的评价结果。本文选取SROCC指标作为图像质量评价算法性能的指标,同时绘制拟合曲线定性地评价无参考评价算法的性能。
3.3 实验结果及分析
为了更直观体现无参考图像质量评价算法的性能,本文在LIVE 数据库[46]上对PSNR 和SS-SSIM 两种经典的全参考图像质量评价算法,以及本文介绍的无参考图像质量评价算法进行了性能测试。
本文所有程序采用Matlab 源代码,支持向量机采用Libsvm 工 具 包,运 行 环 境 为Intel®CoreTMi3,主 频 为3.40 GHz 的 处 理 器。其 中,BIQI 与DIIVINE 两 种 算 法是基于两级框架算法,在进行SVM 分类时,采用的是径向基函数方法(Radial Basis Function,RBF),以5 重交叉验证的方式确定SVM 参数;采用v-SVM 进行回归训练,(c,γ,ν)参数采取与SVM 同样的交叉验证方式进行确定,其中ν取确定值0.5(实验表明,ν值对算法性能影响较小)。BRISQUE 算法训练回归模型同样采用的是径向基函数,(c,γ,ν)3 个参数中,γ设为0.05,(c,ν参数为libsvm 工具箱的默认值。对于GRNN 算法,采用MATLAB 工具箱中的newgrnn 函数,参数T设为经验值0.03。
同时,本文还引入了两种广泛使用的全参考图像质量评价算法与文中的无参考算法进行对比,分别是峰值信噪比(Peak Signal to Noise Ratio,PSNR,PSNR)与结构相似度(Structural Similarity Index,SSIM)[10],文献[10中的SSIM算法没有考虑图像多尺度特性,一般称之为单尺度图像结构相似度(Single Scale SSIM,SS-SSIM)。
峰值信噪比PSNR计算公式为,
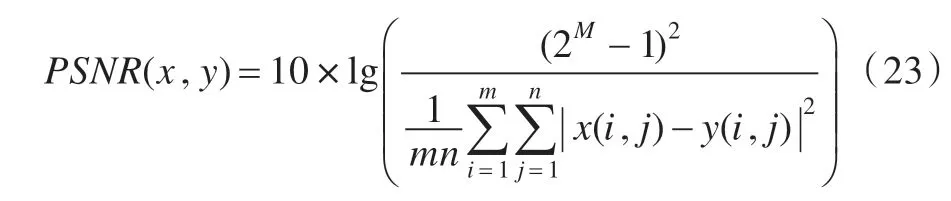
式中的M表示图像像素的比特数(一般图像均为8 bit),x与y分别表示参考图像与失真图像,m与n表示图像的高度与宽度。SS-SSIM 算法的计算公式为,
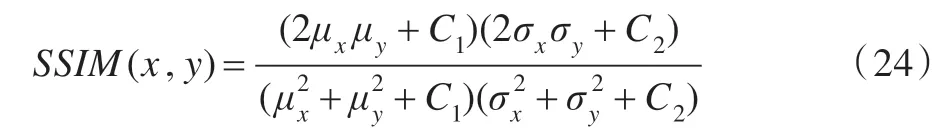
式中的μx与μy表示图像的均值,σx与σy表示图像的方差,C1=K1L,C2=K2L,L表示图像动态范围(L=255),本文取K1=0.01,K2=0.03。
表1 为两种经典全参考图像质量评价算法(PSNR SSIM)与本文介绍的无参考图像质量评价算法的SROCC性能指标对比和对于不同失真类型的平均运行时间对比,加粗的数字表示各种失真情况下评价算法最优的SROCC值。
为了更直观地评价几种无参考评价算法的性能,本文在LIVE 数据库上,将表1 所示的几种评价算法针对5种失真的客观评价结果与数据库中的主观数据——平均主观评分(Mean Opinion Scores,MOS)进行了一致性比较,如图3 所示。图(a)~(h)表示各种算法针对5 种失真的一致性图,图中的每一个离散点的横坐标表示测试图像客观质量,纵坐标表示主观质量。利用公式(20)的logistic 函数对图中所有的离散点进行非线性拟合,图中红色的曲线是用拟合结果绘制的曲线。
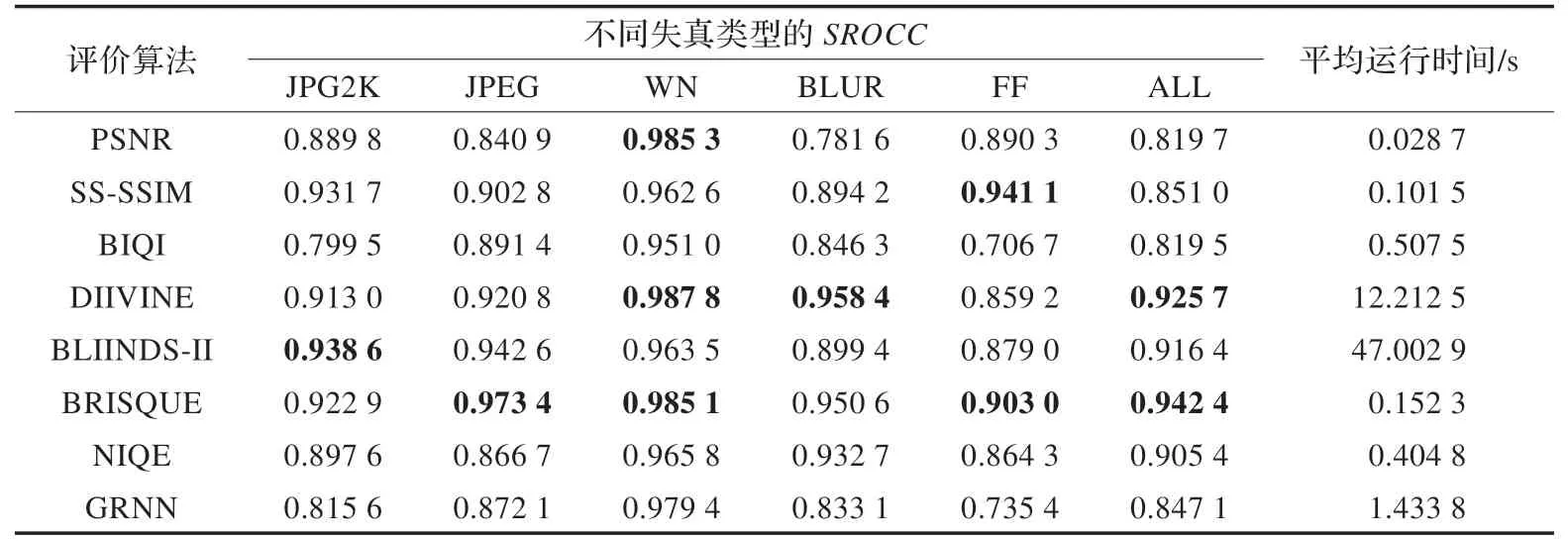
表1 SROCC 和程序平均运行时间对比结果
实验结果分析如下:
(1)SROCC 性能分析
由表1 可以看出,BRISQUE 与DIIVINE 两种算法的SROCC性能最好,分别为0.942 4和0.925 7;BLIINDS-II和NIQE 算法的SROCC性能较好,SROCC性能最差的是GRNN 和BIQI 算法,分别为0.847 1 和0.819 5,其SROCC低于全参考质量评价算法SS-SSIM。
如图3所示,从离散点与拟合曲线的聚合程度可以看出,BIQI算法对白噪声的评价性能最优,但对其他4种失真类型评价性能较差;DIIVINE 算法对白噪声与模糊评价性能最优,对快衰落失真评价性能最差;BLIINDS-I算法对JPEG 与JPEG2000 评价性能较优;BRISQUE 算法对JPEG2000、白噪声、模糊等3 种失真类型评价性能最优;NIQE 算法对白噪声的评价性能较优,总体性能与PSNR相当;GRNN算法对于所有失真类型评价性能均较差。综合图3分析可知,BRISQUE、DIIVINE、BLIINDS-I 3 种算法性能最优,BIQI 与GRNN 算法性能较差,得到了与表1 一致的结论。
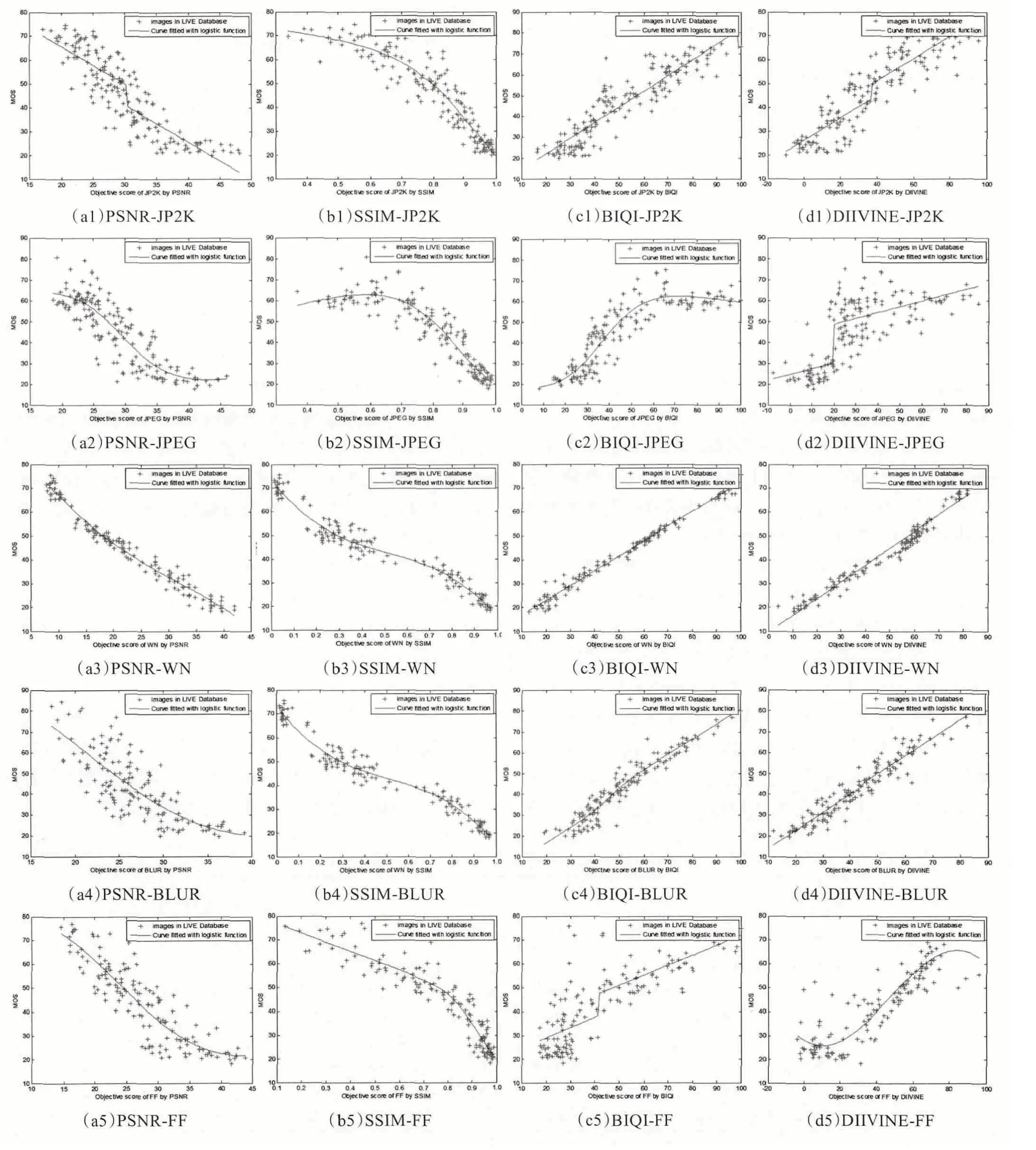
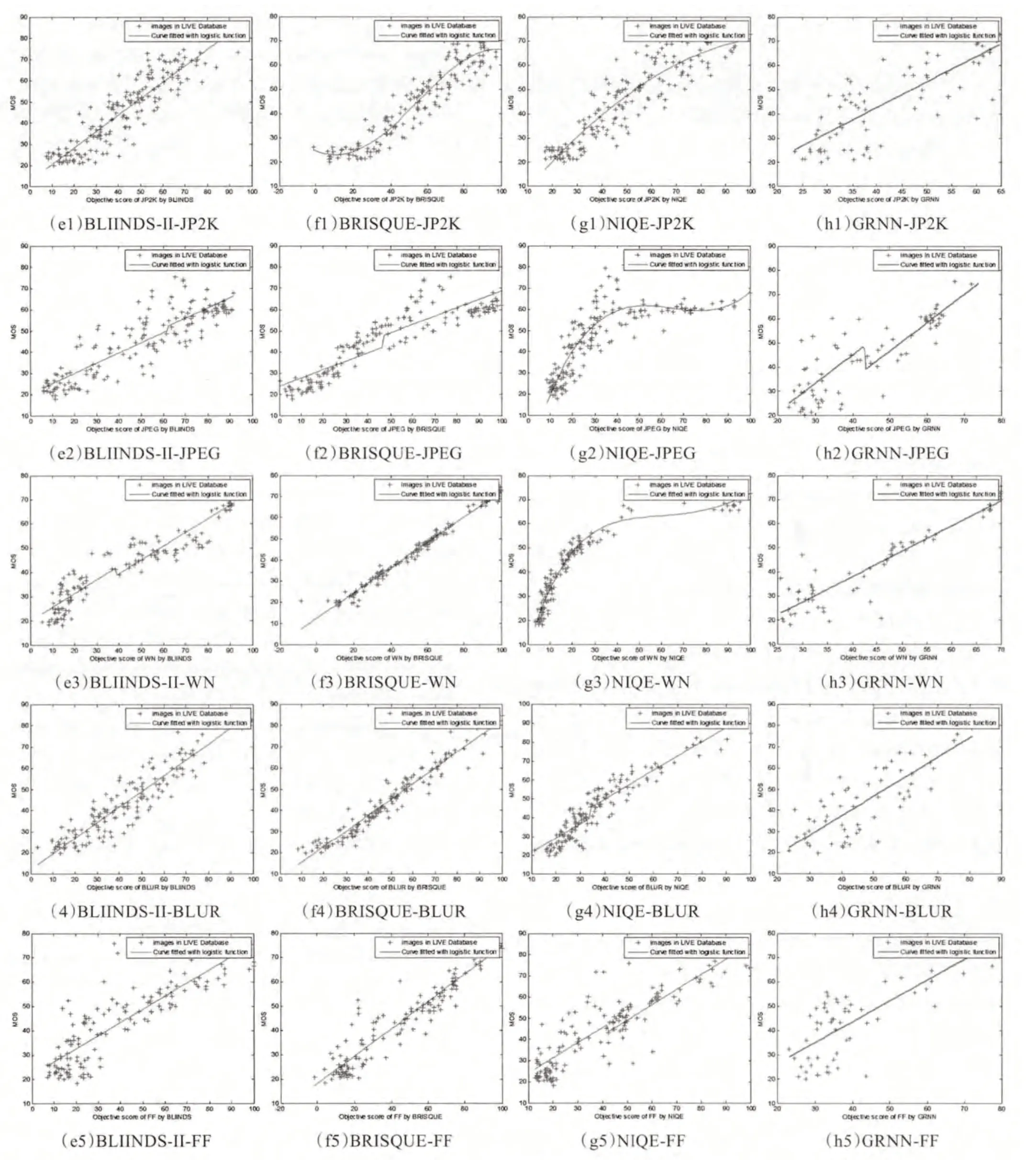
图3 图像客观评价与主观评价的一致性比较
DIIVINE 与BIQI 两种算法都是基于两级框架的小波域特征算法,但DIIVINE 对归一化小波系数提取了更加符合人眼视觉的特征,因此DIIVINE 的性能优于BIQI算法。DIIVINE 与BIQI 两种算法在执行图像特征模型训练时需要已知失真类型,已知条件相对比较苛刻。
BLIINDS 系列算法是基于分块DCT 域特征的评价算法,针对JPEG 和JPEG2000 这类的编码失真取得了很好的评价效果。
BRISQUE 和NIQE 两种算法是基于空域特征提取的算法,BRISQUE 算法对5 种失真类型的评价都取得比较好的效果;NIQE 算法的SROCC性能要差一些,但它是一种“完全无参考”的算法,其训练过程不依赖于任何主观质量数据,克服了实际应用中缺乏主观评价数据的限制。
GRNN 算法严重依赖于主观训练数据,另外由于提取的特征较少,计算结果与主观质量一致性较差。
(2)时间效率分析
从表1可以看出,BRISQUE的平均运行时间最短,仅为0.152 3 s,与全参考算法中SS-SSIM 的平均运行时间0.101 5 s 接近,但算法性能明显优于SS-SSIM;平均运行时间较长的是NIQE、BIQI和GRNN算法,分别为0.404 8 s、0.507 5 s 和1.433 8 s;平均运行时间最长的是DIIVINE和BLIINDS-II算法,分别为12.212 5 s和47.002 9 s。
DIIVINE 算法由于对图像进行了运算复杂度较高的小波变换,并且特征计算较复杂,因此其运行速度比较慢;BLIINDS-II 算法需要进行分块DCT 变换,也大大影响了其运行速度。
BRISQUE 和NIQE 两种算法是基于空域特征提取的算法,其相对于变换域算法的一个显著优势就是算法执行速度快。BRISQUE 的平均运行时间分别为DIIVINE 和BLIINDS-II的1.2%和0.3%。
(3)综合性能分析
从SROCC性能和平均运行时间两方面综合分析本文所述的几种无参考图像质量评价算法,综合性能最优的是BRISQUE 算法,其次是NIQE 算法。DIIVINE 和BLIINDS-II 算法虽然其SROCC 指标较好,但其算法运行时间很长,在实际应用中具有很大的局限性。在实际应用中,由于其NIQE 在对图像进行评价时不需要参考数据库中已有的主观评价数据,因此具有很好的前景。
4 今后研究方向
本文介绍的几种无参考图像质量评价算法虽然已经具有很好的效果,但很多算法在评价时严重依赖于数据库中的主观评价数据,并且在评价精度和算法复杂度方面还存在一些不足,今后可从以下几个方面展开研究:
(1)突破算法对于图像失真类型的限制。因为图像失真类型种类繁多,而且往往并不是相互独立的,一幅视觉质量较差的图像,往往是由于多种图像失真共同作用的结果。因此,对于需要已知训练图像失真类型的一些算法显然是不切实际的。
(2)研究与人眼的视觉效应相关的图像统计特征。利用HVS 特性,研究者已经取得了很大的成功,然而想要更好地模拟人眼的视觉效应,这需要神经学、生物学和心理学等多学科之间的共同发展。
(3)增加图像的彩色信息。色彩信息也是一种重要的视觉信息,全参考图像质量评价算法已经成功地将彩色信息运用到算法中,如FSIM(Feature Similarity Index for Image Quality Assessment)算法[51],而目前几乎所有的无参考图像质量评价算法都是在灰度图像上进行的。
(4)提高算法的运行速度。无参考图像质量评价算法主要注重于网络多媒体的应用,因此需要提高图像质量评价算法的实时性。
5 结束语
本文对当前经典的几种通用型无参考算法进行了综述,并在LIVE 数据库上进行了性能测试。无参考质量评价算法在数字多媒体领域具有广阔的应用前景,通用型无参考算法将会是图像质量评价领域的研究热点,本文的通用型无参考评价算法综述对深入理解无参考图像质量评价算法有着重要的意义。
[1] 高新波,路文.视觉信息质量评价方法[M].西安:西安电子科技大学出版社,2010:105-108.
[2] Feng X J,Allebach J P.Measurement of ringing artifact in JPEG images[C]//Proc of SPIE,2006.
[3] Meesters L,Martens J B.A single-ended blockiness mea sure for JPEG-coded images[J].Signal Processing,2002,82(3):369-387.
[4] Wang Z,Sheikh H R,Bovik A C.No-reference perceptua quality assessment of JPEG compressed images[C]//Pro ceedings of IEEE International Conference on Image Pro cessing,2002:477-480.
[5] Shan S.No-reference visually significant blocking artifac metric for natural scene images[J].Signal Processing,2009,89(8):1647-1652.
[6] Tong H,Li M,Zhang H J,et al.Noreference quality assess ment for JPEG2000 compressed images[C]//Proceeding of International Conference on Image Processing,2004,5:3539-3542.
[7] Marziliano P,Dufaux F,Winkler S,et al.Perceptual blu and ringing metrics:Application to JPEG2000[J].Signa Processing:Image Communication,2004,19(2):163-172.
[8] Sazzad Z M P,Kawayoke Y,Horita Y.No reference image quality assessment for JPEG2000 based on spatial fea tures[J].Signal Processing:Image Communication,2008,23(4):257-268.
[9] Sheikh H R,Bovik A C,Cormack L.No-reference quality assessment using natural scene statistics:JPEG2000[J]IEEE Transactions on Image Processing,2005,14(11):1918-1927.
[10] Wang Z,Bovik A C,Sheikh H R,et al.Image quality assess ment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612
[11] Caviedes J,Oberti F.A new sharpness metric based on local kurtosis,edge and energy information[J].Signal Processing Image Communication,2004,19(2):147-161.
[12] Ferzli R,Karam L J.A no-reference objective image sharpness metric based on the notion of Just Noticeable Blur(JNB)[J].IEEE Transactions on Image Processing,2009,18(4):717-728.
[13] Zhu X,Peyman M.A no-reference sharpness metric sensitive to blur and noise[J].Quality of Multimedia Experience,2009(1):64-69.
[14] 桑庆兵,苏媛媛,李朝锋,等.基于梯度结构相似度的无参考模糊图像质量评价[J].光电子·激光,2013,24(3):573-577.
[15] 邵宇,孙富春,刘莹.基于局部结构张量的无参考型图像质量评价方法[J].电子与信息学报,2012,34(8):1779-1785.
[16] 范媛媛,沈湘衡,桑英军.基于对比度敏感度的无参考图像清晰度评价[J].光学精密工程,2011,19(10):2485-2493.
[17] Moorthy A K,Bovik A C.A two-step framework for constructing blind image quality indices[J].Signal Processing Letters,2010,17(5):513-516.
[18] Moorthy A K,Bovik A C.Blind image quality assessment:from natural scene statistics to perceptual quality[J].IEEE Transactions on Image Processing,2011,20(12):3350-3364.
[19] Unser M,Chenouard N,Van D,et al.Steerable pyramids and tight wavelet frames in[J].IEEE Transactions on Image Processing,2011,20(10):2705-2721.
[20] Wainwright M J,Schwartz O,Simoncelli E P.Natural image statistics and divisive normalization:Modeling nonlinearities and adaptation in cortical neurons[M].Massachusetts,USA:MIT Press,2002:203-222.
[21] Saad M A,Bovik A C,Charrier C.A DCT statistics-based blind image quality index[J].Signal Processing Letters,2010,17(6):583-586.
[22] Saad M A,Bovik A C,Charrier C.DCT statistics modelbased blind image quality assessment[C]//Proceedings of the 18th IEEE International Conference on Image Processing(ICIP),2011:3093-3096.
[23] Mittal A,Moorthy A K,Bovik A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactions on Image Processing,2012,21(12):4695-4708.
[24] Ruderman D L.The statistics of natural images[J].Network:Computation in Neural Systems,1994,5(4):517-548.
[25] Mittal A,Soundararajan R,Bovik A C.Making a“completely blind”image quality analyzer[J].Signal Processing Letters,2013,20(3):209-212.
[26] Li C F,Bovik A C,Wu X J.Blind image quality assessment using a general regression neural network[J].IEEE Transactions on Neural Networks,2011,22(5):793-799.
[27] 贾惠珍,孙权森,王同罕.结合感知特征和自然场景统计的无参考图像质量评价[J].中国图象图形学报,2014,19(6):859-867.
[28] 李朝锋,唐国凤,吴小俊,等.学习相位一致特征的无参考图像质量评价[J].电子与信息学报,2013,35(2):484-488.
[29] 金波,李朝锋,吴小俊.结合NSS 和小波变换的无参考图像质量评价[J].中国图象图形学报,2012,17(1):33-39.
[30] Sheikh H R,Sabir M F,Bovik A C.A statistical evalua tion of recent full reference image quality assessmen algorithms[J].IEEE Transactions on Image Processing,2006,15(11):3440-3451.
[31] Srivastava A,Lee A B,Simoncelli E P,et al.On advance in statistical modeling of natural images[J].Journal o Mathematical Imaging and Vision,2003,18(1):17-33.
[32] Sharifi K,Leon-Garcia A.Estimation of shape paramete for generalized Gaussian distributions in subband decom positions of video[J].IEEE Transactions on Circuits and Systems for Video Technology,1995,5(1):52-56.
[33] Simoncelli E P,Freeman W T,Adelson E H,et al.Shift able multiscale transforms[J].IEEE Transactions on Infor mation Theory,1992,38(2):587-607.
[34] Wainwright M J,Simoncelli E P.Scale mixtures of Gauss ians and the statistics of natural images[J].Adv Neura Information Processing Systems,2000,12:855-861.
[35] Sharifi K,Leon-Garcia A.Estimation of shape paramete for generalized Gaussian distributions in subband decom positions of video[J].IEEE Transactions on Circuits and Systems for Video Technology,1995,5(1):52-56.
[36] Lasmar N E,Stitou Y,Berthoumieu Y.Multiscale skewed heavy tailed model for texture analysis[C]//Proceeding of the 16th IEEE International Conference on Image Processing(ICIP),2009:2281-2284.
[37] Martin D,Fowlkes C,Tal D,et al.A database of human segmented natural images and its applications to evalu ating segmentations algorithms and measuring ecologica statistics[C]//Proc of International Conference on Com puter Vision,2001,2:416-423.
[38] Bishop C M.Pattern recognition and machine learning[M]New York:Springer,2006:93-94.
[39] Kirsanova E N,Sadovsky M G.Entropy approach in the analysis of anisotropy of digital images[J].Open System and Information Dynamics,2002,9(3):239-250.
[40] Gabarda S,Cristóbal G.Blind image quality assessmen through anisotropy[J].JOSA A,2007,24(12):B42-B51.
[41] Huang T,Burnett J,Deczky A.The importance of phase in image processing filters[J].IEEE Transactions on Acous tics,Speech and Signal Processing,1975,23(6):529-542.
[42] Oppenheim A V,Lim J S.The importance of phase in signals[J].Proceedings of the IEEE,1981,69(5):529-541.
[43] Morrone M C,Owens R A.Feature detection from loca energy[J].Pattern Recognition Letters,1987,6(5):303-313 x]m,]:
[44] Venkatesh S,Owens R.An energy feature detection scheme[C]//Proceedings of IEEE International Conference on Image Processing,5-8 September,1989.
[45] Specht D F.A general regression neural network[J].IEEE Transactions on Neural Networks,1991,2(6):568-576.
[46] Sheikh H R,Wang Z.Live image quality assessment database[EB/OL].(2005)[2010-06-14].http://live.ece.utexas.edu/research/Quality/.
[47] Ponomarenko N,Lukin V,Zelensky A,et al.TID2008-A database for evaluation of full reference visual quality assessment metrics[J].Advances of Modern Radio Electronics,2009,10(5):30-45.
[48] Ponomarenko N,Jin L,Ieremeiev O,et al.Image database TID2013:Peculiarities,results and perspectives[J].Signa Processing Image Communication,2015,30:57-77.
[49] Rohaly A M,Libert J,Corriveau P,et al.Final report from the video quality experts group on the validation o objective models of video quality assessment[J].ITU-T Standards Contribution COM,2000(1):9-80.
[50] Sheikh H R,Sabir M F,Bovik A C.A statistical evalua tion of recent full reference image quality assessmen algorithms[J].IEEE Transactions on Image Processing,2006,15(11):3440-3451.
[51] Zhang L,Zhang D,Mou X Q.FSIM:A feature similarity index for image quality assessment[J].IEEE Transaction on Image Processing,2011,20(8):2378-2386.

