制图综合中河流与建筑物拓扑冲突处理方法
赵彬彬
ZHAO Binbin
长沙理工大学 交通运输工程学院,长沙410004
School of Traffic and Transportation Engineering,Changsha University of Science&Technology,Changsha 410004,China
1 引言
空间数据不一致性即空间目标之间存在明显的矛盾或冲突[1],其存在极大地影响空间数据质量,降低空间数据可用性,亦因此日益受到国际地理信息学界基础研究领域的关注[2]。空间数据集成及制图综合操作易导致空间目标之间的冲突,进而产生不一致性[3-4]。综观已有不一致性相关成果,现有研究多针对相同或相近比例尺地图数据空间目标之间的不一致性[5-6],近来亦有一些学者开始研究空间数据集成或数据库更新中的不一致性问题,针对河流与等高线之间的不一致性研究成果逐渐丰富起来[3,7]。然而,随着制图综合技术在生产中的广泛深化应用[8-10],由综合操作引起的不一致性问题日渐受到关注,其中代表性研究包括:Kang 和Li 提出了基于拓扑属性严密分类规则,并用于评价和探测由“Collapse”综合操作引起的拓扑不一致性[11]。Du 等基于“Merging”和“Dropping”制图综合操作提出了针对宽边界复杂面目标的结构和拓扑不一致性评价方法[12],上述研究基本是针对制图综合过程中某一种或两种不一致性的探测和评价,而在处理层面则进展缓慢亦无突破,部分悬而未决的不一致性问题仍未得到有效合理的解决[13]。例如,对面目标的“简化”操作导致A、B 两目标之间距离关系的不一致,如图1(a)和(b)中红圈位置所示;对河流的“光滑”操作造成建筑物C 与河流D 之间拓扑冲突,如图1(c)和(d)。为此,本文主要针对制图综合操作导致的河流与建筑物之间的拓扑不一致性问题,提出了一种利用Morphing 变换技术并综合考虑建筑物,综合前后河流边界在距离约束条件下的拓扑冲突处理新方法,对比实验亦证明了该方法的有效性。

图1 制图综合导致的不一致性
2 问题分析及解决方案
分析上述河流与建筑物之间的拓扑冲突不难看出,由较大比例尺河流综合派生较小比例尺河流的操作一方面略去了许多弯曲细节,提高了其概括程度,另一方面又改变了河流边界的空间位置,使河流与建筑物由综合前的拓扑“相离”变为综合后的拓扑“相交”,进而导致拓扑冲突,其表现形式为建筑物“落入”河流中,而深层原因则是概括后的河流边界位置变化。如图1(c),综合前,河流D 的边界弯曲细节明显,其局部几何形状与建筑物C 的北部轮廓较吻合;综合后,如图1(d),河流D 的边界弯曲细节被概括,其图中红圈所示的局部几何形状亦不再与建筑物轮廓相吻合,河流边界位置亦变动至建筑物一侧,并穿过建筑物C,进而产生拓扑冲突。因此,综合概括时既要考虑河流的概括趋势又要避免其与建筑物之间的拓扑矛盾,可取的解决方案为:根据综合前后河流局部边界位置并顾及建筑物边界进行线性插值以获得新的综合后的河流边界。具体处理步骤如下:
(1)将较小比例尺河流和较大比例尺河流分别记为RS和RL并求差,获得可能的不一致区域集合Reg{r|r⊂RSr⊄RL}。
(2)取集合Reg{·}中的区域rk,判断rk与一定缓冲范围内(如以道路宽度为缓冲半径)的建筑物面目标是否相交,若不相交,则将其从集合Reg{·}中移除,由此获得不一致区域集合Zint{·},若集合Zint{·}为空,则转至步骤(6)。
(3)遍历集合Zint{·}中区域zi,将zi与相交的建筑物求差获得剔除不一致区域的待插值区域z_inti,进而依次获取z_inti与较大比例尺河流的公共边界Bd_Lari及与较小比例尺河流和建筑物的公共边界Bd_Smai。
(4)分别以Bd_Lari和Bd_Smai为端点,运用Morphing变换方法在两端点之间插值,并顾及插值边界与建筑物边界之间的距离约束ContD,从而获得最佳插值边界OptBdi。
(5)从较小比例尺河流区域中减去插值边界OptBd与原冲突边界构成的区域,从而获得处理后的较小比例尺河流。
(6)不一致处理结束。
3 不一致边界的插值处理
3.1 Morphing 变换
本文采用的插值方法为Morphing 变换。Morphing变换是一种基于连续变形思想、同时顾及形状和颜色以实现计算机图像无缝平滑渐变的内插技术[14],已广泛应用于影视特技、图像压缩及游戏娱乐等计算机可视化领域[15]。目前,Morphing 变换在地理信息科学领域多应用于对不同比例尺道路、河流等线目标的形状内插[16]。下面简要说明Morphing 变换过程,如图2,(a)中两个细节程度不同的线目标E 和F 分别代表较大比例尺地图和较小比例尺地图中的原始目标,即Morphing 变换的起点和终点;(b)为在E 和F 之间沿直线移位路径进行Morphing 插值,通过移位距离值t(t∈[0,1])控制插值结果与起点或终点的接近程度。若t越接近于0,则插值结果的位置与起始目标E 越接近,细节特征更相似;若越接近于1,则插值结果的位置与终止目标F 越接近,几何特征相似度亦更高。若t=0,则插值结果为起始目标E;若t=1,插值结果即为终止目标F。图2(b)为分别采用0.2、0.5 以及0.9 作为移位距离的三个不同插值结果。

图2 不同移位距离值与Morphing 变换插值结果
3.2 空间距离关系约束
由上述插值示例可以看出,不同移位距离使插值结果与起始目标和终止目标的接近程度各不相同,即在插值区域中的插值结果并不唯一,若移位距离过小,则会使插值结果与较大比例尺目标相似度过高,其细节保留亦较多,对待综合目标的概括作用有限;若移位距离过大,则会使插值结果与较小比例尺目标的相似度增大,两者空间位置也将过近,当两者距离小于肉眼能够分辨的图上最小距离时,视觉上给人以河流与建筑物已相接的错觉,无法和综合前河流与建筑物的拓扑“相离”关系保持一致。为此,参照相关标准,本文将人眼对图上最小距离的分辨率0.1 mm 作为插值结果与建筑物之间的距离关系约束[17]。
4 拓扑冲突处理实例
按照第2 章的处理步骤,采用两组不同比例尺的河流和居民地数据进行实验(如图3 和图4),并与Delaunay 三角剖分骨架中轴线法进行对比。
4.1 Morphing 变换插值处理
如图3,对于河段一,(a)和(b)分别为综合前后的河流与建筑物面目标,对比可以发现,综合操作导致河流与建筑物之间两处拓扑冲突,分别为(c)中的建筑物G 与河流I和(d)中的建筑物H与河流I。如图4,对于河段二,(a)和(b)分别为综合前后的河流与建筑物面目标,对河段二的综合操作共产生四处拓扑冲突,分别为(c)、(d)、(e)和(f)中的建筑物J、K、L 和M 与河流N 之间的拓扑冲突。
按第2 章所述步骤运用Morphing 插值法对两个河段的六处冲突进行处理。如图5,对于第一个河段局部①的冲突,(a)为获取的河流I 与建筑物G 之间的拓扑冲突范围;(b)为剔除建筑物G 的Morphing 插值区域;(c)为由插值区域提取的插值边界,即Morphing 变换起点和终点;(d)为顾及距离约束获得的河流边界插值结果(红色线目标),即插值结果与建筑物之间的最小距离不小于图上0.1 mm,此插值结果对应的移位距离值为0.13,如图5(e);(f)为Morphing 插值结果与综合操作前较大比例尺河流边界之间的对照。类似地,图6 为对第一个河段局部②的冲突处理过程,该插值结果对应的移位距离值为0.35。

图3 河段一与建筑物之间拓扑冲突

图4 河段二与建筑物之间拓扑冲突
针对第二个河段,如图7(因受文章篇幅限制,此处仅列出图4(b)中局部③和局部⑤的冲突处理过程及结果,另两处冲突的处理及结果类似),(a)为获取的河流N 与建筑物J 之间的拓扑冲突范围;(b)为剔除建筑物J的Morphing 插值区域;(c)为由插值区域提取的插值边界,即Morphing 变换起点和终点;(d)为顾及距离约束获得的河流边界插值结果(红色线目标),即插值结果与建筑物之间的最小距离不小于图上0.1mm,此插值结果对应的移位距离值为0.09,如图7(e);(f)为Morphing 插值结果与综合操作前较大比例尺河流边界之间的对照。类似地,图8 为对第二个河段(图4(b))局部⑤冲突的处理过程,该插值结果对应的移位距离值为0.12。
4.2 Delaunay 三角剖分骨架中轴线法
如图9,(a)~(c)和(d)~(f)分别为Delaunay 三角剖分提取骨架线法对河段一与建筑物之间的两处冲突区域(局部①和局部②)进行处理,通过提取Delaunay 三角剖分骨架中轴线作为处理结果[18]。如图9(c),对于局部①的冲突,一方面,三角剖分骨架中轴线虽与建筑物之间拓扑“相离”,但两者过度接近,与红色标示的Morph ing 插值结果比较可见,其与建筑物之间的图上距离已明显小于人眼最小距离分辨率(红色箭头所示),不满足距离关系约束;另一方面,中轴线出现近乎直角的转折,如(c)中红圈所示,增加了河流边界的细节,与综合操作的概括意图不相符。对于局部②的冲突,如图9(f),红圈所示处“尖锐”的中轴线与建筑物之间为拓扑“相接”,拓扑冲突仍未消除。图10 为运用Delaunay 三角剖分提取骨架线法对河段二与建筑物之间两处冲突(局部③和局部⑤)的处理结果,亦出现上述类似问题。可见,Delaunay 三角剖分骨架中轴线法存在与两个不同比例尺河流边界几何形态相似度低且无法有效处理此类拓扑冲突等不足。

图5 河段一局部①的冲突处理实验

图6 河段一局部②的冲突处理实验

图7 河段二局部③的冲突处理实验

图8 河段二局部⑤的冲突处理实验

图9 河段一局部①和②的Delaunay 三角剖分骨架中轴线处理结果及其对比
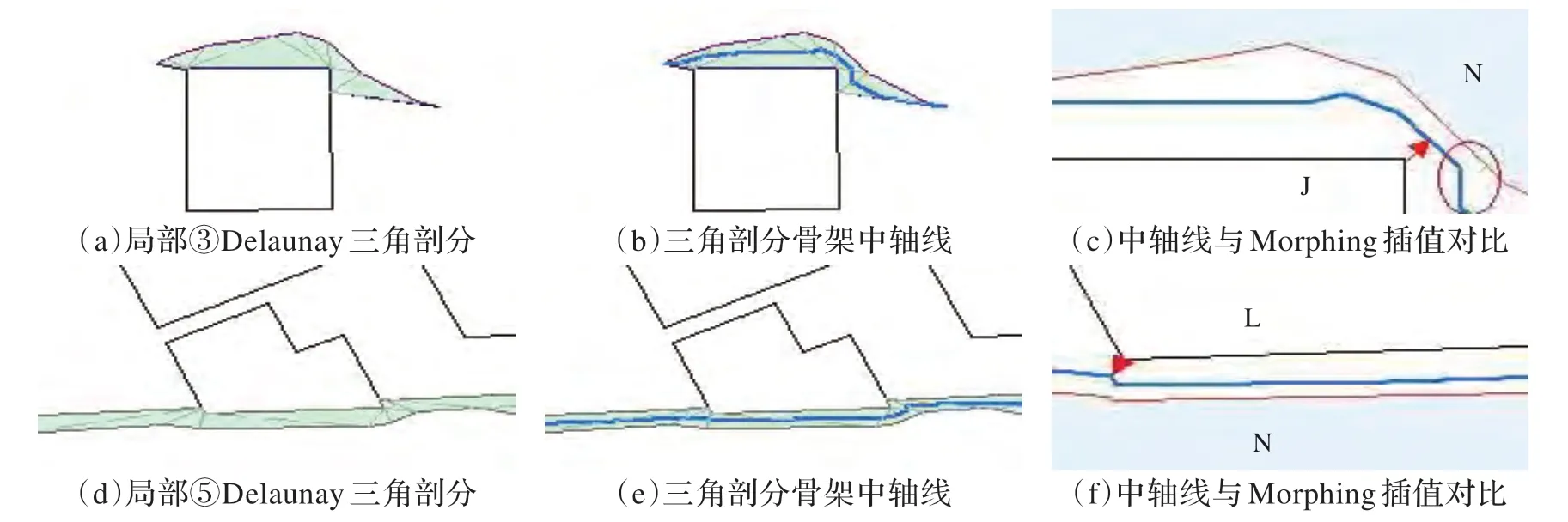
图10 河段二局部③和⑤的Delaunay 三角剖分骨架中轴线处理结果及其对比
5 结论
社会经济持续发展的现实需求对实时准确、协调一致的地理空间数据提出了更高要求,随着制图综合技术的日益进步与广泛应用,对制图综合过程中不一致性问题的研究将更具有现实意义和应用价值[2,19]。本文借助Morphing 变换技术的“交叉溶解”特点[14],尽可能地保留了两种不同比例尺地图河流边界的几何形态特征,提出了将建筑物从拓扑冲突区域中剔除的处理方法,只需考虑空间距离约束,简化了目标之间的空间操作运算环节,减小了计算量,进而提高了拓扑冲突处理效率。相对于Delaunay 三角剖分骨架中轴线法而言,本文方法的处理结果在几何形状以及与综合概括趋势的契合度等方面表现均较好,实验结果亦验证了其有效性。后续工作将研究本文方法在等高线、道路与建筑物等相关不一致性处理方面的拓展应用[20]。
[1] Rodríguez M A.Inconsistency issues in spatial databases[J]Lecture Notes in Computer Science,2005,3300:237-269.
[2] Li D R,Zhang J X,Wu H Y.Spatial data quality and be yond[J].International Journal of Geographical Informa tion Science,2012,26(12):2277-2290.
[3] AiTinghua,Yang Min,Zhang Xiang,et al.Detection and correction of inconsistencies between river networks and contour data by spatial constraint knowledge[J].Cartography and Geographic Information Science,2015,42(1):79-93.d:]::
[4] Ruiz J J,ArizaF J,Ureña M,et al.Digital map conflation:a review of the process and a proposal for classification[J].InternationalJournal of Geographical Information Science,2011,25(9):1439-1466.
[5] 简灿良,赵彬彬,邓敏,等.地理空间数据不一致性探测处理方法研究[J].计算机工程与应用,2013,49(10):150-155.
[6] 詹陈胜,武芳,翟仁健,等.基于拓扑一致性的线目标空间冲突检测方法[J].测绘科学技术学报,2011,28(5):387-390.
[7] Chen J,Liu W,Li Z,et al.Detection of spatial conflicts between rivers and contours in digital map updating[J].International Journal of Geographical Information Science,2007,21(10):1093-1114.
[8] 王家耀.地图制图学与地理信息工程学科发展趋势[J].测绘学报,2010,39(2):115-119.
[9] 王家耀,钱海忠.制图综合知识及其应用[J].武汉大学学报:信息科学版,2006,31(5):382-386.
[10] 费立凡.用计算机模拟人类制图员解决地图缩编中的图形冲突[J].武汉大学学报:信息科学版,2004,29(5):426-432.
[11] Kang H K,Li K J.Assessing topological consistency for collapse operation in generalization of spatial databases[J].Lecture Notes in Computer Science,2005,3770:249-258.
[12] Du S H,QinQ M,WangQ,et al.Evaluating structural and topological consistency of complex regions with broad boundaries in multi-resolution spatial databases[J].Information Sciences,2008,178(1):52-68.
[13] Li Z L.Algorithmic foundation of multi-scale spatial rep resentation[M].Bacon Raton:CRC Press(Taylor & Fran cis Group),2007:279-280.
[14] Li Z L,Wong M L.Animating basic operations for digita map generalization with morphing techniques[C]//Pro ceedings of the International Archives of the Photo grammetry,Remote Sensing and Spatial Information Science(Part B2),Beijing,China,2008:637-642.
[15] 东晨,宋松和.非结构网格下曲线变形的水平集方法[J].计算机工程与应用,2010,46(29):186-188.
[16] 彭东亮,邓敏,赵彬彬.河网多尺度Morphing 的变换方法研究[J].遥感学报,2012,16(5):953-968.
[17] 中华人民共和国国家质量监督检验检疫总局.GB/T 20257.2—2006 国家基本比例尺地形图图式 第2 部分:1∶5 000 1∶10 000地形图图式[S].北京:中国标准出版社,2006.
[18] 陈学工,陈树强,王丽春.基于凸壳技术的Delaunay 三角网生成算法[J].计算机工程与应用,2006,42(6):27-30.
[19] Corcoran P,Mooney P,Winstanley A.Planar and non-plana topologically consistent vector map simplification[J].Inter national Journal of Geographical Information Science,2011,25(10):1659-1680.
[20] 吴小芳,杜清运,胡月明,等.基于改进Snake模型的道路网空间冲突处理[J].测绘学报,2008,37(2):223-229.

