球形内检测器在海底立管内通过性仿真研究

陈世利，高春倩，郭世旭，黄新敬

CHEN Shili,GAO Chunqian,GUO Shixu,HUANG Xinjing

天津大学 精密测试技术及仪器国家重点实验室，天津300072

State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China

1 引言

海底管道作为海上油气集输的主要手段已成为海洋油气资源开发和运输的生命线。由于海底表层地基不稳定、介质腐蚀、海流冲淘及海上作业等原因，海底油气管道易发生油气泄漏事故，造成巨大的经济损失与海洋环境污染[1-2]。为了消除管线运行的潜在安全隐患，必须及时准确地检测和定位海底管道微小泄漏。

目前管道泄漏检测方法可分为外检测法和内检测法。广泛应用于陆地管道的负压波法[3-4]、声波相关法[5]、光纤泄漏法[6-8]等管道外检测法仅能够检测大于总流量1%的原油泄漏和大于总流量5%的天然气泄漏[9]，在海底管道的泄漏检测中尚未见有效应用，因为如此大的油气泄漏在海面上已能发现。海底油气管道需要的是微小泄漏检测技术。管道内检测法依靠内检测器从管道内靠近泄漏点监听泄漏信号，理论上能够检测到十分微小的油气泄漏。传统的管道内检测器（Pipeline Inspection Gauge，PIG）在前后压力差的作用下前进[10-12]，获得管道内壁的腐蚀、缺陷以及焊缝状况等，通过壁面缺陷来判断是否存在泄漏。但PIG 体积庞大，且与管壁紧密贴合，对管道变形十分敏感，存在高卡堵风险。而海底管道在洋流作用下易发生几何变形，进一步限制了其在海底管道的应用。

为了解决海底管道微小泄漏检测的迫切需求，本课题组于2007 年首次提出了一种球形内检测器[13]，能够识别和精确定位0.1 L/min 的微小泄漏。球形载体在管道内流体的推动下滚动前进，沿途记录管道内泄漏信号和定位信息。由于球形载体外径小于管道内径，且是滚动前进，所以不仅结构简单，不易卡堵，而且噪声小，检测精度高[14-16]。然而，海底管道经常存在高达数百米的立管段[17]，若球形内检测器不能顺利通过立管段不仅无法实现微小泄漏检测与定位，还会影响管道正常运行，甚至诱发重大安全事故。因此对球形内检测器在海底管道立管段的通过能力的研究至关重要。

本文采用有限元仿真方法对球形内检测器在海底管道立管段的通过性进行研究。为了验证仿真方法的正确性，搭建实验平台管道，并设计不同模型球（球体密度、球体大小）。文中使用流体计算软件Fluent 14.0，对实验平台立管道内模型球周围流场进行三维数值仿真并计算模型球顺利通过立管段的临界速度，通过与实验所得临界速度进行比较，验证仿真方法的正确性。采用该仿真方法，对实际海底管道立管段球形内检测器的通过性及影响因素进行预测分析。

2 模型和数值分析

2.1 立管内球体受力分析

以立管段内球体为研究对象，如图1 所示，理想条件下，球体在管道内仅受到Ff,Ft和G的作用，Ft为竖直向上的推力，由流体压力以及流体速度能量作用于球体上产生，Ff和G分别为球体所受浮力和重力是为已知量，竖直方向受力分析得：

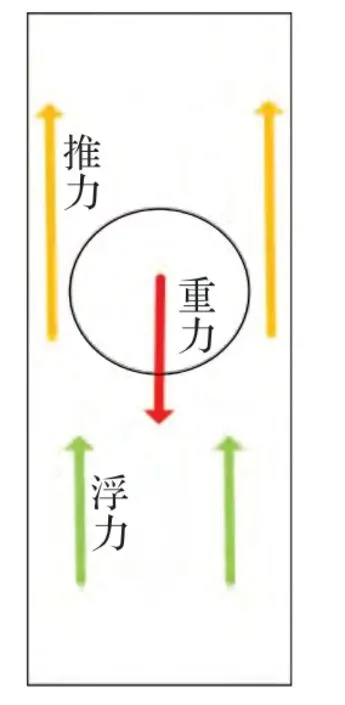
图1 竖直管道球体受力分析

显然，当Fh＞0 时，球体能顺利通过竖直管道，使Fh=0 的Ft即为临界推力，对应流体速度为临界流速。因此，求得Ft根据式（1），即可判断球体是否能顺利通过竖直管道，本文采用有限元仿真方法求解管内流体对球体的推力Ft。

2.2 管内流体数学模型

流体绕过球体在竖直管道内的流动为湍流，且流体为不可压缩介质，因此管道内流体流动遵循湍流运输方程，本文选用标准k-ε湍流模型。任何流体的流动都满足质量守恒方程和动量守恒方程，则笛卡尔坐标系下管道内流体流动遵循如下控制方程[18]：

（1）质量守恒方程

式中ρ表示管内流体密度，t表示时间，u表示速度矢量，由于管内流体流动处于稳态，则密度ρ不随时间变化，公式（2）简化为：

（2）动量守恒方程

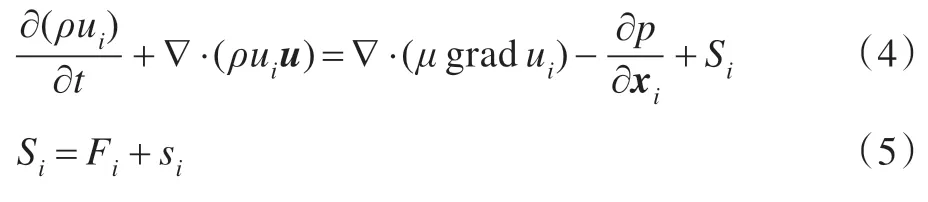
式中，μ是动力粘度，p是管内流体微元体上的压力，ui是u沿x、y、z方向的分速度，Si是动量守恒方程的广义源项，Fi是微元体上的体力，由于管道内流体是粘性为常数的不可压缩流体，则si=0。

（3）不可压缩流体的运输方程

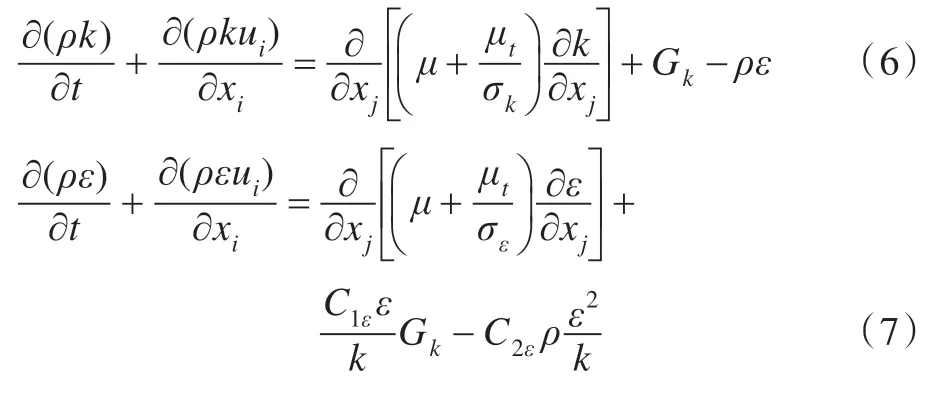
其中，C1ε=1.44,C2ε=1.92,σk=1.0,σε=1.3,σk、σε分别是与湍动能k和耗散率ε对应的Prandtl 数，C1ε、C2ε为经验常数。由以上控制方程经流体计算软件fluent14.0计算可得管道内各微元体上的压力p和速度u。

2.3 数值分析

由于直接搭建与实际管道尺寸相同的推力验证实验平台十分困难，本文并未直接对球形内检测器在海底管道立管段的通过性进行仿真计算和实验验证，而是将实际模型尺寸等比例缩小后进行数值模拟，并针对小模型搭建实验平台，设计和制作模型球，以验证仿真方法的正确性。实际球形内检测器样机如图2 所示，球壳密度为2 700 kg/m3的铝壳，内部搭载有加速度计、磁力计以及音波传感器等，其平均密度为1 300 kg/m3。仿真计算和实验中对该极限密度（2 700 kg/m3）和平均密度（1 300 kg/m3）模型球在管道内的运动进行考察，根据实际选材难易情况，选择密度为1 420 kg/m3聚甲醛和密度为2 700 kg/m3铝分别制作模型球进行研究。同时为了便于仿真结果和实验结果多组比较，设计多种尺寸实验模型球，直径d分别为8 mm、16 mm、20 mm、24 mm、30 mm、32 mm。

图2 实际球形内检测器

2.3.1 网格划分

几何模型如图3 所示，管道内径D为40 mm，流体经过模型球时，管内流场经历了稳定，剧烈变化到稳定的过程，为了保证出入口处的流动均是稳定的，计算域上游L2 取1.5 m，下游L1 取4 m。采用ANSYS ICEM CFD 14.0 网格生成软件对模型进行网格划分，生成网格如图4。

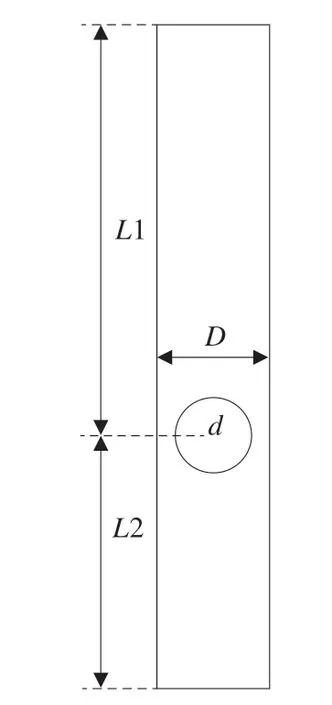
图3 几何模型图

图4 六面体网格图

整个计算域为六面体结构化网格，相对于其他类型网格，使用更少的网格节点获得更高精度结果。其中采用了3 个O-grid 对模型进行细分，球面边界外部用O-grid 进行网格加密，采用等比例拉伸的结构网格来加密球体附近管道网格，疏化远离球体管道网格，使网格能体现计算域内流场的变化趋势，网格数量约180 万，经检验符合网格独立性要求。

2.3.2 边界条件和离散格式

实际应用中流速是已知可调节量，因此入口边界条件定义为速度入口，方向垂直于边界，入口流速为0.2～1.5 m/s，出口边界条件为压力出口，其余边界条件均定义为壁面边界条件，默认无滑移壁面条件，粗糙度常数为0.5，管内流体为水，密度为999.4 kg/m3，动力粘度为0.001 Pa·s，温度以实验温度为准，为19 ℃。流体在管道内流动时，管壁区流场情况变化很大且存在粘性底层，标准k-ε湍流模型不能完全真实地描述管内流体流动，因此采用标准壁面函数改善近壁区域数值计算结果。流场计算采用Simple 算法进行压力修正，且用二阶迎风差分格式离散动量方程。

2.3.3 仿真结果分析

采用前述数学模型、上述边界条件和离散格式等，应用Fluent 14.0软件对管道内流场进行数值计算，图5（a）和图5（b）给出了流速相同时不同直径球体所在管道流场的总压力分布。

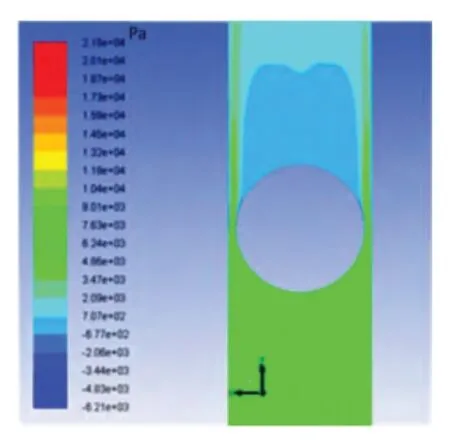
图5 （a）直径32 mm 球体总压力云图

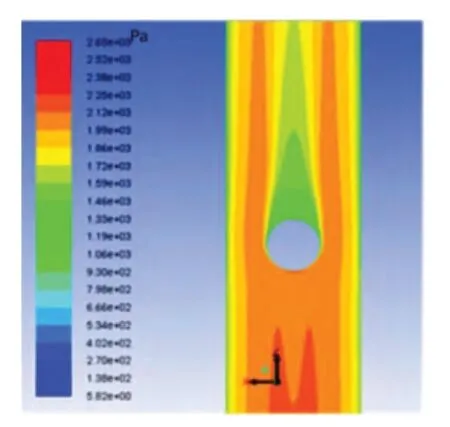
图5 （b）直径16 mm 球体总压力云图

图5（a）中球体直径较大，球体上部两侧流场存在负压区，上部附近流场为低压区，这是由流体流经球体后形成的尾迹发展的；图5（b）中球体直径较小，球体周围流场的压力均为正压力，上部附近流场也存在低压区，但面积较小。由图5（a）和图5（b）平面板的压力值可以看出，直径较大球体周围流场压力值远远高于直径较小球体周围流场的压力值，由此可以初步断定直径大球体所受流体推力较大，相同密度球体通过同一管径管道时所需流速较小。

3 仿真与实验对比

3.1 仿真结果计算

如图5（a）和图5（b），仿真计算出管内流场各处压力，应用Fluent 计算流体对球体竖直方向推力。推力产生原因除压力外，还包括粘性力。Fluent 计算球面沿竖直方向所受的合力大小等于球面各处压力和粘性力与竖直向上矢量a点积加和的积分，计算公式如下：

其中：a·Fp为球面某点压力沿竖直向上方向的分力，a·Fu为球面某点粘性力沿竖直向上方向的分力，a为沿竖直向上方向的单位矢量，Fp为球面某点压力矢量，Fu为球面某点粘性力矢量。

通过上述方法计算得竖直管道内流体对球体竖直方向的推力。本文采用有限元仿真方法对管道内流体进行仿真分析，由式（8）计算得Ft。为了得出不同模型球通过竖直管道的临界速度，对仿真所得数据进行处理分析。

图6（a）为不同直径模型球的推力-流速数据点曲线，观察数据点曲线和二次多项式曲线极为相似，因此采用Polyfit[19]函数对推力和流速进行二次多项式拟合，拟合曲线如图6（b）所示，同时得到推力-流速拟合方程和数据点的相对误差δ如表1 所示。

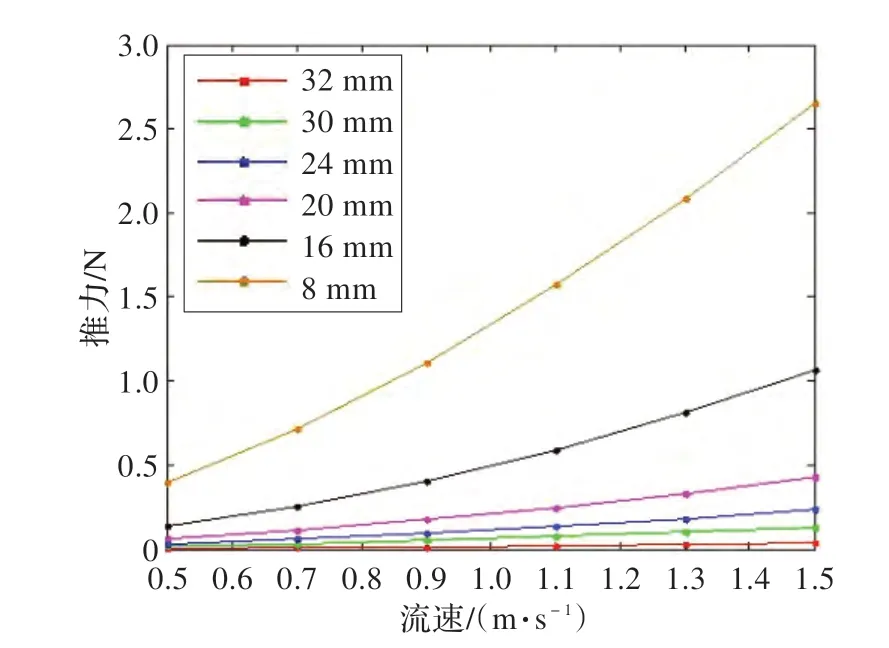
图6 （a）不同直径模型球推力-流速数据点曲线

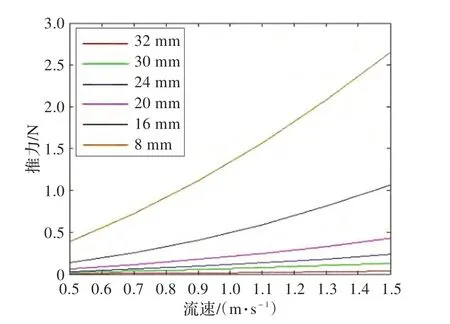
图6 （b）不同直径模型球推力-流速拟合曲线

表1 推力-流速拟合方程

由表1 可知相对误差在0.5%内，可见拟合效果很好，推力与流速成二次函数关系。

已知模型球密度和直径，结合公式（1）和拟合得到的推力-流速拟合方程，求得不同直径聚甲醛和铝质模型球在管道内能够上升的临界速度ul,如表2 所示。

表2 聚甲醛和铝模型球的临界速度

3.2 实验结果分析

图7 为搭建的实验平台流程图，设计时主要考虑因素有：（1）为方便观察模型球在管道内的运动情况，管道选用透明有机玻璃管。但受有机玻璃加工工艺限制，弯管段选用钢管，竖直和水平管道段为有机玻璃管。（2）考虑真实钢材和钢材弯头的标准件尺寸，钢管弯管段角度为90°和135°。（3）为方便实验时能多次快速地投球和收球，设计了收发球装置。（4）在流体入口处安装有针型阀和流量计，用于调节和显示管道内流体流速。（5）为避免污染实验场地，实验装置整体组成一个循环系统，流体在管道内循环流动。

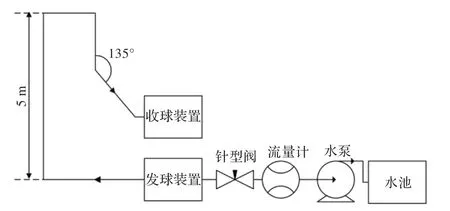
图7 实验平台流程图

管道内流体为水，动力粘度为0.001 Pa·s，温度为19 ℃。实验时水池中的水经水泵流入实验管道内，当水充满管道后，将不同直径的聚甲醛和铝质模型球分别投入实验管道，调节针型阀改变管道内水的流速使球体在竖直管道内悬浮，通过流量计读取其临界速度ul',最后增大流速对模型球进行回收。表3 为实验读取的临界速度ul'及实验与仿真结果的误差e。

实验与仿真存在一定误差，误差产生主要有以下原因：

（1）针型阀调节流速时流量计读数反应慢，与管内流体流速存在一定滞后，流量计读数有一定偏差。

（2）实验条件与仿真条件存在一定的差异，如调节流速时存在压力的突变等。

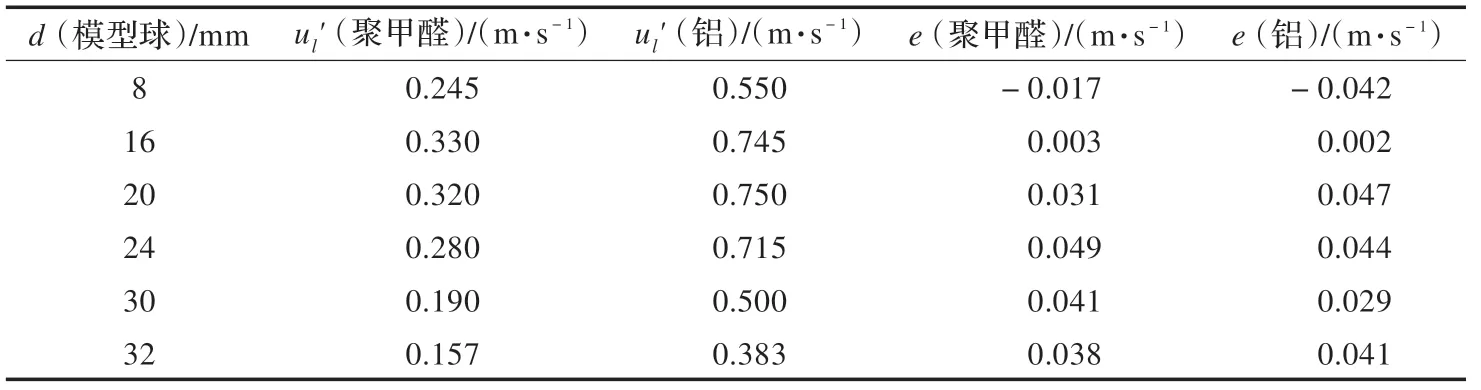
表3 实验结果及误差

（3）流体中夹杂少量气泡，影响实验结果。

由表3 可知，误差范围为－0.05～0.05 m/s，此误差在工程应用中是可接受的，仿真结果和实验结果基本吻合。这说明此仿真方法是正确的，仿真结果真实可靠，可以用于预测球形内检测器海底管道立管段的通过能力。

4 通过性影响因素分析

应用上述仿真方法分别对球形内检测器在8～28 inch立管段时管内流场进行数值模拟，实际工况下管内流体流速为0.8～1.2 m/s，因此选取仿真流速为0.8～1.2 m/s，流体为石油。结合公式（6）计算流体对球形内检测器的推力，再结合公式（1）得出球形内检测器在海底管道立管段受到的合力，应用差值方法[20-21]对合力做曲面拟合，拟合曲面如图8 所示。

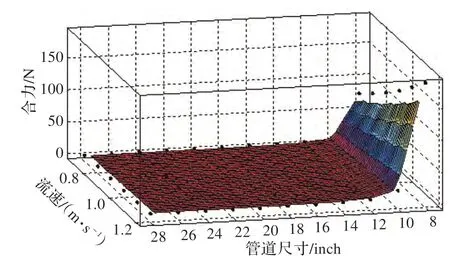
图8 实际工况合力拟合曲面

由图8可以看出，当管径不变时，随着流速的增加球形内检测器的合力增大，但当管道直径较大时推力随流速增加不明显，且合力均小于零，球形内检测器不能通过海底管道立管段；当管道直径为10 in 和8 in 时，即球管径比达到73%时，其合力明显增大，且合力随流速增加而增加显著，此时合力均大于零，球形内检测器均能通过海底管道立管段。可得结论：球形内检测器直径不变时，管道直径越小，即球管径比越大，球形内检测器所受推力和合力越大。球管径比是一个重要的参数，也是影响球体在管道立管段通过性的主要因素，当球管径比达到73%时，球形内检测器在正常工作流速0.8～1.2 m/s内，均能顺利通过海底管道立管段。

5 结束语

本文对采用有限元仿真方法对球形内检测器安全通过性及其影响因素进行研究，主要得到了以下结论。

（1）通过Fluent 仿真立管道内球体周围三维流场，比较仿真结果和实验结果，验证了仿真方法是正确的，其结果真实可信，此仿真方法可用于预测对球形内检测器在海底管道立管段的通过性。

（2）在管径和球体直径保持不变时，竖直管道内球体所受推力和流速呈二次函数关系。

（3）球管径比对球形内检测器在海底管道立管内的通过性来说是一个很重要的参数，球管径比大于等于73%时，在其正常工况流速（0.8～1.2 m/s）下即可通过。

[1] 覃觅.石油泄漏灾难[J].资源与人居环境，2006（11S）：64-67.

[2] 晓武.石油泄漏，海洋面临生态之痛[J].节能与环保，2011（9）：36-39.

[3] 邵煜，葛传虎，叶昊，等.基于负压波的管道泄漏检测与定位系统评价[J].油气储运，2008，27（4）：5-9.

[4] Tian Chunhua，Yan Junchi，Huang Jin，et al.Negative pressure wave based pipeline leak detection：challenges and algorithms[C]//Proceedings of IEEE International Conference on Service Operations and Logistics and Informatics，2012.

[5] 华科，叶昊，王桂增，等.基于声波的输气管道泄漏检测与定位技术[J].华中科技大学学报：自然科学版，2009，37（8）：181-183.

[6] Tu Y，Chen H.Design of oil pipeline leak detection and communication system based on optical fiber technology[C]//Proceedings of SPIE 1999，1999，3737：584-592.

[7] 周琰，靳世久，张昀超，等.分布式光纤管道泄漏检测和定位技术[J].石油学报，2006，27（2）：121-124.

[8] Paranjape R，Liu N，Rumple C，et al.A distributed fiber optic system for oil pipeline leakage detection[C]//Proc of SPIE 2003，Feb 1，2003，4833.

[9] 袁朝庆，庞鑫峰，刘燕.管道泄漏检测技术现状及展望[J].大庆石油学院学报，2006（2）：76-79.

[10] 宋志东，靳世久，李一博，等.管道内检测器里程轮信号优选算法的设计与实现[J].管道技术与设备，2006（3）：12-13.

[11] 刘保余，綦耀光.输气管道内检测器设计及理论研究[D].北京：中国石油大学，2010.

[12] 张立军，綦耀光，刘保余，等.输气管道内检测器模型试验系统的设计[J].管道技术与设备，2010（2）：26-27.

[13] 郭世旭.检测输油管道泄漏的球形内检测器：中国，201110402319.3[P].2012-05-09.

[14] Chen Shili，Guo Tingting.A length measuring method based on accelerometer[C]//Proceedings of the 1st International Conference on Instrumentation，Measurement，Computer，Communication and Control，2003.

[15] 刘渊，陈世利，郭世旭，等.输油管道微小泄漏球形检测器的设计与实现[J].传感器与微系统，2012，31（6）：130-133.

[16] 赵伟.油气管道内磁场特性分析及应用研究[D].天津：天津大学，2012.

[17] 黄鑫，余建兴.海底管线设计分析[D].天津：天津大学，2004.

[18] 王福军.计算流体动力学分析[M].北京：清华大学出版社，2004.

[19] 饶秀勤，应义斌.自适应滤波器在水果声学特性研究中的应用[J].浙江大学学报：农业与生命科学版，2003（2）：28-31.

[20] 彭芳瑜，周云飞，周济.基于插值与逼近的复杂曲面拟合[J].工程图学学报，2002（4）：88-96.

[21] 兰凤崇，陈吉清，郑世红，等.散乱数据的曲面拟合及其在汽车车身外表面造型设计中的应用[J].吉林工业大学学报，1996（3）：10-15.