基于FLcom 的模糊知识推理与搜索处理

赵洁心，潘正华，王姗姗

ZHAO Jiexin,PAN Zhenghua,WANG Shanshan

江南大学 理学院，江苏 无锡214122

School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China

1 引言

在知识表示与知识推理等研究中，对于知识中的否定的认知和处理一直以经典逻辑为基础。随着知识处理研究的发展，近年来一些学者主张知识处理领域中需要两种否定。自1991 年，Wagner 等人区分强否定（strong negation）表示明确的假（explicit falsity）和弱否定（weak negation）表示非-真（non-truth）[1-5]。2005 年Kaneiwa 在描述逻辑中主张两种否定，从而提出一个带有经典否定和强否定的扩展的描述逻辑ALC～。2006 年Ferré提出一种认识的扩充，即基于模态逻辑AIK（All I Know）的一种逻辑转化运用在逻辑概念分析LCA（Logical Concept Analysis）的框架中[6]。2006 年潘正华等人从概念层面上提出在知识处理中区分知识的矛盾关系和对立关系，研究指出了清晰性知识和模糊性知识中存在五种矛盾否定关系与对立否定关系，给出了它们的一种逻辑描述，并运用在知识表示与知识推理中[7-9]。为了能够从逻辑的角度描述模糊知识中的不同否定及其关系与规律，2013 年潘正华又提出一种区分矛盾否定、对立否定和中介否定的模糊命题逻辑形式系统FLcom，并讨论了其特有的性质与意义，给出了FLcom 的一种语义解释[10]。

本文基于模糊命题逻辑形式系统FLcom 描述模糊知识，对带有多种否定的模糊知识推理及搜索处理做了研究，将模糊知识以模糊命题的形式表现出来，并根据FLcom 对模糊命题形式表示和语义解释将知识推理规则用模糊命题合式公式表示，合理定义了推理规则中结点否定形式的算子。给出实现搜索的算法和交通事故模型中模糊知识的推理过程与搜索结果。

2 基础

2.1 单链表

单链表[11]是线性表的一种非顺序存储表示，属于非数值计算领域的数学模型—线性结构的范畴。单链表用一组地址任意的存储单元存放线性表中的数据元素。表中的一个单元可以看成一个结点，每个结点除了存放数据以外，必须设一个指针域，便于联接下一个结点。数据域用来存储结点的值；指针域用来存储数据元素的直接后继的地址（或位置）。

这里采用尾插法建立单链表[12]。头指针head 指向头结点，并设置两个指针r、s。起始状态是三个指针同时指向头结点。申请新结点为s指向，修改指针r→next=s，最终r结点指向终端结点。如图1 所示。

图1 单链表的建立

由单链表的建立过程可以知道单链表中借用指针来表示数据元素间的逻辑关系，且每个结点仅包含一个指向后继元素的指针。单链表只可向一个方向遍历。表中的数据元素对应的结点包括两个域：指针域和数据域。

2.2 区分矛盾否定、对立否定和中介否定的模糊命题逻辑形式系统FLcom

定义1[10]（I）设S是非空集，其元素称为原子命题或原子公式，“¬”，“ ╕”，“～”，“→”，“∧”和“∨”是连接词，“（”与“）”是括号。规定：

（1）对每个A∈S，A是模糊命题。

（2）若A和B是模糊命题，则¬A，╕A，～A，(A→B)，(A∨B)和(A∧B)是模糊命题。

（3）由（1）与（2）生成的全体模糊命题集为ℑ(S)，简记为ℑ。ℑ 中的元素称为模糊公式，简称公式。

（II）ℑ 中的以下公式称为公理：

（A1）A→(B→A)

（A2） (A→(A→B))→(A→B)

（A3） (A→B)→((B→C)→(A→C))

（M1） (A→¬B)→(B→¬A)

（M2） (A→╕B)→(B→╕A)

（H） ¬A→(A→B)

（C） ((A→¬A)→B)→((A→B)→B)

（∨1）A→A∨B

（∨2）B→A∨B

（∧1）A∧B→A

（∧2）A∧B→B

（Y ╕） ╕A→¬A∧¬～A

（Y～） ～A→¬A∧¬╕A

（III）推理规则MP（Modus Ponens）：由A→B与A推出B。

由（I）、（II）和（III）构成的形式系统，称为区分矛盾否定、对立否定和中介否定的模糊命题逻辑形式系统FLcom（Fuzzy propositional Logic with Contradictory negation，Opposite negation and Medium negation）。

FLcom是基于模糊集FScom基础上提出的一种区分矛盾否定、对立否定和中介否定的模糊命题逻辑形式系统。在FScom 中，已证明一个模糊集P的矛盾否定P¬与对立否定P╕和中介否定P～具有关系：P¬=P╕∪P～，根据上述，即是¬P=╕P∪～P。

在FLcom 中模糊公式¬A，╕A和～A的关系定义如下[10]：

定义2在FLcom 中，¬A=╕A∨～A。

2.3 FLcom 的一种语义解释

定义3[10]设λ∈(0,1)。映射∂：ℑ →[0,1]称为ℑ的一个λ-赋值，如果：

（1）∂(A)+∂(╕A)=1

（2）∂(～A)=

（3）∂(A∨B)=max(∂(A),∂(B)),∂(A∧B)=min(∂(A),∂(B))

（4）∂(A→B)=ℜ(∂(A),∂(B))

这里ℜ ：[0,1]2→[0,1]是某个二元函数。

定义4[10]（λ-重言式）设ℑ是Σ的λ-赋值集，∀A∈Σ。如果对每个ξ∈ℑ，恒有ξ(A)=1，则称A为ℑ-重言式。如果λ＞1/2 时，使得对每个λ-赋值ξ，恒有ξ(A)≥λ，则称A为λ-重言式。

3 模糊知识的状态空间表达式

3.1 基于模糊命题逻辑形式系统FLcom 的模糊命题表示

模糊命题主要由模糊概念构成，模糊命题的真值函数本身也必须与现实概念结合起来才有意义。要描述推理规则中的模糊命题，首先要对模糊命题中涉及的模糊概念进行描述。在对概念进行描述时，首先应确定对应类具有相同内涵的全体语言概念的集合，选取此内涵的更高级概念中区别最大的两个模糊概念最为对立概念，并将其中之一用相应的[0，1]上的模糊子集表示[8]。由文献[13]知，其余概念对应的表示可以得出。从而模糊命题及其不同否定也可以表示出来。

在数据库中，知识以规则形式存在。设其中某个原子模糊命题为P，沿用FLcom 中的符号，其矛盾的模糊命题即表示为¬P，对立的模糊命题为╕P，中介模糊命题为～P，或者可以根据需要将不同的模糊命题组合成合式公式来表达各种复杂的事实和命题。如此，对于命题¬P，╕P，～P，可以根据不同的前缀做出相应的处理。这样大大减少了数据库中原子模糊命题的存储量，减少了搜索时间。

为利于计算机实现，只研究规则库中含有FLcom 中的逻辑连接词的情况。因而，在知识表示中也仅含逻辑连接词：“¬”，“ ╕”，“～”，“→”，“∧”和“∨”。在不考虑阈值时，将每条规则表示为“A→B，CF”形式，其中A、B为原子模糊命题或合式公式，CF表示此规则的置信度。

3.2 命题逻辑公式的单链表的表示

在推理过程中，推理规则中往往不是一个条件推出一个结果，会出现多个条件推出一个结果或一个条件推出多个结果的情况，而且不是所有的条件之间都有联系，一个条件也会在不同的推理规则中出现。因而，将单链表的定义修改为：

定义5在单链表中，一个存储单元为一个结点，每个单元保存两个数据项，第一个数据项是数据（即原子模糊命题的形式表示与其真值），第二个数据项是指针，即与下一个结点的逻辑关系。在内存中指针域就是后继结点的集合。结点之间用箭头连接，箭头上的数字表示箭头连接的两个结点之间关系的置信度。箭头可以表示结点之间“蕴含”，“交”关系，即“→”，“∧”。

定义6规则路径表是存储推理规则、结点置信度、规则可信度并用于搜索处理的一种若干单链表的组合表，即它是由规则中若干个既含有数据域又含有指针域的多个结点链接而成的一种存储结构，且每个结点与其后继结点按顺序存储在内存表中，所有的逻辑推理与搜索处理都以既定规则为准。

下面就用单链表和规则路径表表示模糊推理规则：

（1）多个条件推出一个结果：A1,A2,…,An→B，则它 可 分 离 成n条 规 则：A1→B,CF1;A2→B,CF2;…;An→B,CFn，CFi(i=1,2,…,n) 为每条规则的置信度。分离后的规则用单链表表示，并将这些单链表组合成规则路径表，其中A1,A2,…,An，B是结点，如图2 所示。

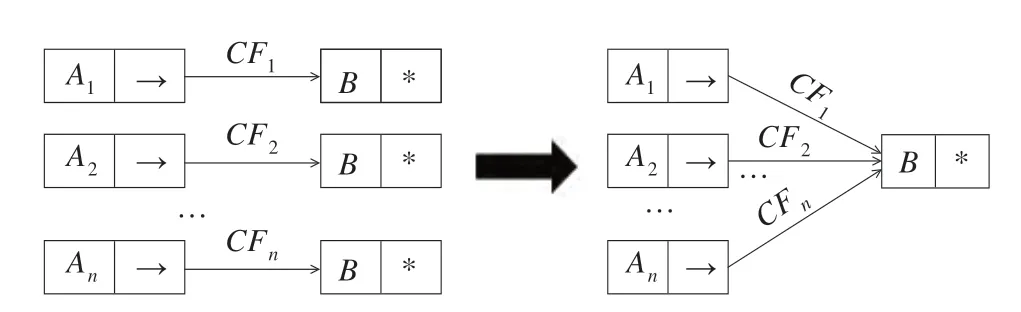
图2 图形演示一

（2）一个条件同时推出多个结果：A→B1,B2,…,Bn，则它可分离成n条规则：A→B1,CF1;A→B2,CF2;…;A→Bn,CFn。CFi(i=1,2,…,n) 为每条规则的置信度。分离后的规则用单链表表示，并将这些单链表组合成规则路径表，其中A,B1,B2,…,Bn是结点，如图3 所示。

图3 图形演示二

对于多维模糊规则：A1∧A2∧…∧An→B，直接用单链表表示，如图4 所示。

图4 图形演示三

如图2、图3、图4 所示，每个规则由结点，结点之间的逻辑关系和置信度组成，当规则运行时，从头指针head 开始，头指针指向单链表中的第一个结点。往往头结点作为输入结点，不同结点及其后继结点依次从存储表中提取出，依照推理规则在规则路径表中展现它的逻辑状态。这样有利于快速搜索，减少数据访问量，提高算法效率。

4 模糊知识推理的搜索方法

4.1 算法分析

在处理模糊知识时，问题的陈述和数据获取方面固有的模糊性使得分析、解决问题时要处理大量模糊性的知识、概念，这样得出的结果往往也具有模糊性。而且根据不同的实际情况可以推断出多种结果，这就需要运用一定的策略得出最合理的结果。

本文用模糊推理的方法解决这一类模糊问题。模糊推理的基本原理就是根据已有的知识，建立推理规则推测未知知识[14]。在多层次模糊知识推理中，希望得到的是可能性最大的结果，因而问题转化为根据已有的模糊推理规则寻找出最可能的结果，从而得出最佳路径。在本文中寻找最佳路径的过程就是寻找综合可信度最大路径问题。

为确定每一个表示模糊规则结论的结点所具有的真值或置信度，本文采用Zadeh 的CRI 算法[15]。Zadeh算子是模糊推理的CRI 框架中所用的t-范[15]，即a∨b=sup{a,b}，a∧b=inf{a,b}，同时也是格运算。基于Zadeh的CRI框架定义启发函数：

f(n)=g(n)∧h(n)=min{g(n),h(n)}

其中，g(n)为头结点到结点n的可信程度；h(n)为结点n到目标的估计可信度。在实际搜索中，可将初始条件真值程度视为头结点的置信度，推理规则的置信度视为结点通过指针到达其后继结点的可信度，推理结果为结点的置信度。

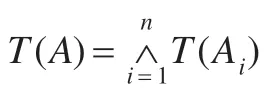
4.2 否定信息的处理

以上所述都是研究结点之间推理关系的推理规则及其表示，对于该文而言，结点就是原子模糊命题。上述搜索过程还需要具备解决结点中包含否定情形的能力，即解决模糊命题的矛盾否定(¬)、对立否定(╕)和中介否定(～)的能力。

在规则库中，多个规则之间通常存在一定联系。但这种联系有时又并非直接，例如：“A→B,CF1；╕B→C,CF2；～B→D,CF3；¬B→E,CF4”。可以看出A与C、D、E之间通过B有间接联系。为在搜索过程中体现这种联系，将B、¬B、╕B、～B都视为A的后继结点，如此便能通过A间接推理到C、D或E。然而此时的问题是，规则库中并没有直接给出A→╕B，A→～B，或A→¬B分别的置信度。在此，可先根据已知的规则求出B的置信度，然后采取一定的方法得出¬B，╕B，～B。为使推理有序进行，在内存中存储结点时将结点按照推理层次存储，规则中的原子模糊命题及其不同否定在一个层次上，一个层次上的结点按指定顺序存储，如：B，¬B，～B，╕B，如果其中的结点没有参与推理，则不需要存储在内存中。

针对具体实际领域，对知识库中的每一个原子模糊命题A(x) 都赋予一个属于[0，1]区间的真值，并确定l（规定λ＞0.5）作为满足命题A的阈值。引用定义3 的符号，记∂(A(x))为原子模糊命题A(x)的真值程度函数。

（1）根据定义3，∂(A)+∂(╕A)=1。因此，令对立否定“ ╕”的算子为：∂(╕A(x))=1-∂(A(x))。

（2）对于中介否定模糊命题～A(x)，由定义3 中式（1）～（5）可知，当λ＞1/2 时～A(x)的真值程度属于区间(1-λ,λ)。但这种语义解释没有考虑A(x)的真值程度属于区间[1-λ,λ]的情况，这样就不能全面处理好否定信息，基于此，给出中介否定“～”的算子：

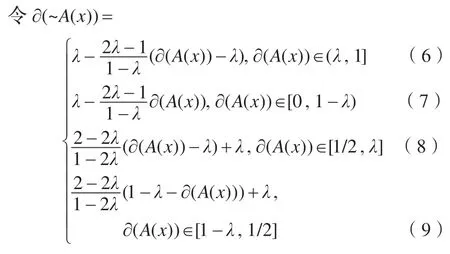
此算子在FLcom 的一种语义解释的基础上进行了修改，更符合人的思维习惯。在中介否定算子中，当λ＞1/2 时，式（6）中，当∂(A(x))的取值从λ（不取λ）过渡到1 时，∂(～A(x)) 从λ（不取λ）依次递减到1-λ（不取1-λ）。式（7）中，当∂(A(x))的取值从0 过渡到1-λ（不取1-λ）时∂(～A(x))从λ（不取λ）依次递减到1-λ（不取1-λ）。式（8）中，当∂(A(x))从1/2过渡到λ时∂(～A(x))从1递减过渡到λ。式（9）中，当∂(A(x))从1-λ过渡到1/2时∂(～A(x))从λ递增过渡到1。特别的，由式（8）、（9）还可以看出，当∂(A(x))越接近1/2时，∂(～A(x))的值越高。当∂(A(x))=1/2 时∂(～A(x))=1，这说明模糊命题A(x) 的模糊度比较高。

（3）根据定义2，有¬A=╕A∨～A。因此，令矛盾否定“¬”的算子为：∂(¬A)=max{∂(╕A),∂(～A)}。

5 具体实现

5.1 实例分析

下面讨论模糊知识的推理与搜索处理的具体实例。推理规则：

（1）中年人是老练而稳重的，可信度较高；

（2）老练、稳重且有驾驶技术的人是不容易出交通事故的，可信度很高；

（3）驾驶技术熟练，熟悉交通规则又清醒驾驶的青年人不容易出交通事故，可信度较高；

（4）年纪大的人若疲劳驾驶较容易出交通事故，可信度较高；

（5）技术熟练的人比较熟悉交通规则，可信度高；

（6）驾驶技术不熟练的人容易出交通事故，可信度很高。

搜索条件：李先生50 岁并驾驶技术熟练；李先生可能有点疲劳。

根据FLcom 将这几条规则转化成模糊命题逻辑形式。令论域为所有人，X属于论域。对于规则置信度，可根据实际情况对表示可信程度的语言赋值。在这个例子中，对“可信度很高”、“可信度较高”和“可信度高”分别赋予规则置信度值0.9、0.75、0.7；对“容易”、“较容易”和“不容易”分别赋予规则置信度值0.6、0.7、0.8。对“可能”赋予规则置信度值0.65。

根据文献[13]，规则中的模糊概念“老年人”是“青年人”的对立否定；“中年人”是“青年人”的中介否定。显然这三个概念内涵相同，但外延不同。将“X是青年人”作为原子模糊命题，表示为YOUNG（X），则～YOUNG（X）表示“X是中年人”；╕YOUNG（X）表示“X是老年人”。将“X是容易出交通事故的”作为原子模糊命题，表示为ACCIDENT（X）；～ACCIDENT（X）表示“X是较容易出交通事故的”；╕ACCIDENT（X）表示“X是不容易出交通事故的”。其余原子模糊命题表示为：AGE（X，Y），表示X的岁数为Y；TACT（X），表示X老练；STEADY（X），表示X稳重；SKILL（X），表示X驾驶技术熟练；¬SKILL（X），表示X驾驶技术不熟练；FAMILIAR（X），表示X熟悉交通规则；～FAMILIAR（X），表示X较熟悉交通规则；TIRED（X），表示X疲劳驾驶；╕TIRED（X），表示X清醒驾驶。

那么，基于FLcom 和原子模糊命题的形式表示可以将规则表示成：

（1）～YOUNG（X）→TACT（X），CF=0.75；～YOUNG（X）→STEADY（X），CF=0.75。

（2）TACT（X）∧STEADY（X）∧SKILL（X）→╕ACCIDENT（X），CF=0.9。

（3）SKILL（X）∧FAMILIAR（X）∧╕TIRED（X）∧YOUNG（X）→╕ACCIDENT（X），CF=0.75。

（4）╕YOUNG（X）∧TIRED（X）→～ACCIDENT（X），CF=0.75。

（5）SKILL（X）→～FAMILIAR（X），CF=0.7。

（6）¬SKILL（X）→ACCIDENT（X），CF=0.9。

搜索条件表示为：AGE（Li，50），SKILL（Li），CF=1；TIRED（Li），CF=0.65。

至此，发现需要确定此例中“李先生是中年人”的置信度。为此，首先选定“X是青年人”作为原子模糊命题。假如“X是青年人”一般认为X的年龄大概是20至30 岁，“X是老年人”一般认为X的年龄大概是60 至80 岁，“X是中年人”是他们之间的中介。此处只涉及到“年龄”这一因素，采用一维欧式距离d(x,y)=|x-y|以及“距离比率函数”[8]求出命题“李先生是青年人”的真值程度，即

其中，d(x,y)表示x，y之间的一维欧氏距离，d(50,60)表示李先生的年龄与观念上某人是老年人之间的距离，d(30,60)表示观念上某人是青年人和某人是老年人之间的距离。两者的比值表示模糊命题YOUNG（Li）的真值程度，由此可知，AGE（Li，50）→YOUNG（Li）的置信度为0.33。

假设阈值为λ=0.8，显然1-λ＜∂(YOUNG(Li))＜λ。根据4.2 节中式（9），∂(～YOUNG(Li))≈0.887，由“ ╕”的算子，∂(╕YOUNG(Li))=1-0.33=0.67。

下面是用规则路径表表现出的搜索处理方法。

如表1，是交通事故模型中结点的存储表；图5 为交通事故模型的搜索过程。

表1 交通事故模型中结点的存储表（头指针）

表1 交通事故模型中结点的存储表（头指针）

存储地址1000 1001 1002 1003 1004 1005 1006 1007数据域AGE（Li，50）（1）YOUNG（X）（0.33）╕YOUNG（X）（0.67）～YOUNG（X）（0.887）TACT STEADY SKILL¬SKILL指针域1001，1002，1003 1006 1010 1004，1005 1005 1006 1008，1009，1010，1013 1012存储地址1008 1009 1010 1011 1012 1013 1014数据域FAMILIAR～FAMILIAR TIRED╕TIRED ACCIDENT（0.6）╕ACCIDENT（0.8）～ACCIDENT（0.7）指针域1011*1012，1014 1013***

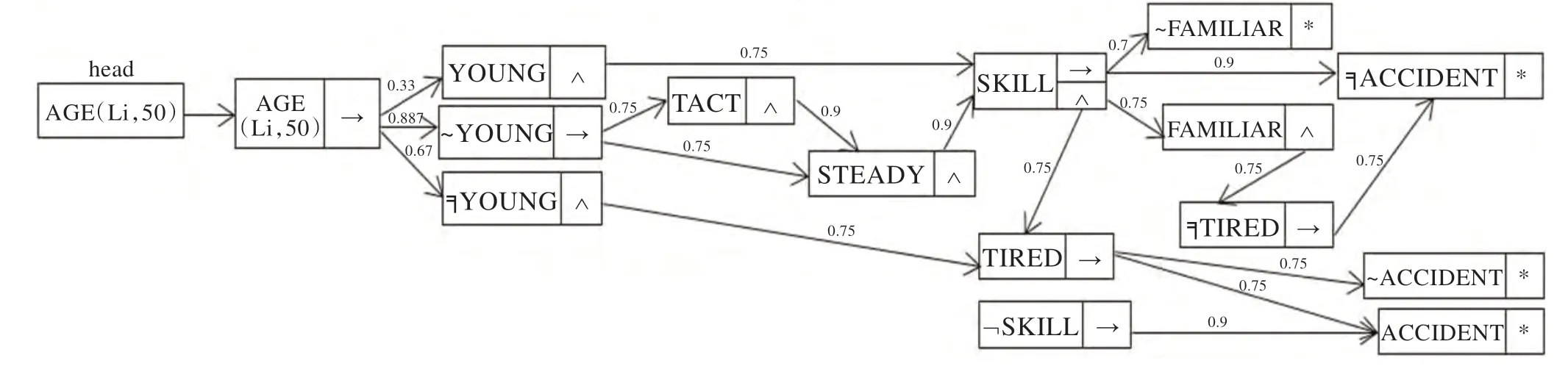
图5 交通事故模型的搜索过程

5.2 算法实现

算法的具体实现过程：

（1）输入初始结点START 作为头结点，根据结点置信度的算子计算此结点的置信度值∂(START)（结点的置信度也有可能依据实际情况事先给定），从内存中依次调用初始结点的指针域。

（2）如果指针域为空，则终止搜索。如果指针域不为空，运用CRI 算法计算指针域中结点的置信度，再提取出置信度值最大的结点（命名为NODE），并记录上一个结点的指针和此结点。再从内存中调用此结点的指针域。

（3）如果指针域为空，则终止搜索，将∂(NODE)赋值给∂(START)。如果指针域不为空，重复步骤（2）。

（4）若∂(START)＜μ则搜索失败；若∂(START)≥μ，则搜索成功。

（5）输出搜索结果∂(START)以及得出这个搜索结果的路径，此搜索路径为最佳搜索路径，结束搜索。

由于推理规则中的原子模糊命题的数量是有限的，所以搜索结点也是有限的，那么算法只需从内存中做有限次的调用，从而算法必在有限步内终止。此算法在搜索过程中，需要规定一个搜索阈值，记为μ。若解结点的置信度值小于μ，则要放弃该搜索，即此解不可信。

根据上述算法的实现过程，由头结点开始通过推理规则搜索可以找到被记录的且满足搜索阈值要求的置信度最高的终端结点。在5.1 节的实例中，将搜索阈值定为0.6。通过算法运行得出∂(AGE(Li,50))=∂(╕ACCIDENT(X))=0.9，即 到 结 点╕ACCIDENT(X)的搜索路径最可信，从而可以推理出李先生不会出交通事故。

6 结束语

基于FLcom，研究模糊知识及其否定的形式表达。合理修改单链表，给出规则路径表的定义，利用规则路径表表示推理规则和搜索过程。结合模糊命题形式系统的语义解释，给出中介否定(～)、对立否定(╕)和矛盾否定(¬)的算子。将模糊知识推理和搜索处理方法、过程应用于交通事故模型，并通过模糊知识搜索处理算法来实现这一搜索过程。这样的处理方法简化了模糊知识推理过程，为模糊推理与搜索处理的计算机实现提供一种新思路。

[1] Wagner G.A database needs two kinds of negation[C]//Proceedings of the 3rd Symposium on MFDSB，May 6-9，1991，495：357-371.

[2] Wagner G.Web rules need two kinds of negation[C]//Proceedings of PPSWR’03，2003：33-50.

[3] Minker J，Ruiz C.Semantics for disjunctive logic programs with explicit and default negation[J].Fundamenta Informaticae，1994，20（3/4）：145-192.

[4] Dung P M，Mancarella P.Production systems need negation as failure[J].IEEE Transactions on Knowledge and Data Engineering，2002，14（2）：336-353.

[5] Vakarelov D.Nelson’s negation on the base of weaker versions of intuitionistic negation[J].Studia Logica，2005，80：393-430.

[6] Ferré S.Negation，opposition，and possibility in logical concept analysis[C]//Proceedings of the 4th International Conference on Formal Concept Analysis，Feb 13-17，2006，3874：130-145.

[7] Pan Zhenghua，Zhu Wujia.A new cognition and processing on contradictory knowledge[C]//Proceedings of the IEEEInternational Conference on Machine Learning and Cybernetics，Qingdao，China，2006：1532-1537.

[8] 王岑，潘正华，程天笑.基于中介逻辑的模糊知识推理的搜处理[J].计算机工程与应用，2009，45（21）：175-178.

[9] 潘正华.知识中不同否定关系的一种逻辑描述[J].自然科学进展，2008，18（11）：66-74.

[10] Pan Zhenghua.Three kinds of negation of fuzzy knowledge and their base of logic[C]//Proceedings of ICIC 2013，July 28-31，2013，7996：83-93.

[11] 谢娟英.单链表不同建立算法研究[J].现代电子技术，2010（4）：132-134.

[12] 史丽燕.单链表基本操作的实现[J].软件导刊，2010（2）：21-22.

[13] 潘正华.模糊知识的三种否定及其集合基础[J].计算机学报，2012，35（7）：1421-1428.

[14] 范世青，张文修.模糊概念格与模糊推理[J].模糊系统与数学，2006（1）：11-17.

[15] 吴望名.模糊推理的原理和方法[M].贵阳：贵州科技出版社，1994.