基于瞬变流法的管道泄漏定位研究

康宪芝，李 健，张 宇，王伟魁，陈瑞东

KANG Xianzhi1,LI Jian1,ZHANG Yu1,WANG Weikui1,CHEN Ruidong2

1.天津大学 精密测试技术与仪器国家重点实验室，天津300072

2.中石油秦皇岛输油气分公司，河北 秦皇岛066200

1.State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China

2.China National Petroleum Corporation Qinhuangdao Company,Qinhuangdao,Hebei 066200,China

1 引言

瞬变流检测法是目前管道泄漏检测中准确性和可靠性都较高的一种方法，因为在瞬变的条件下，即使管道发生微小的泄漏，管道泄漏发生前后管道内的压力波也会发生很大的变化。瞬变流检测法主要通过控制管道末端阀门的关闭引入瞬变流，已经成为近几年国内外研究的热点。

国外Mpesha[1]、Ferrante[2-3]、Wang Xiaojian[4-5]等，国内郭新蕾、杨开林[6-8]、王通[9-10]、白莉[11]、伍悦宾[12]等学者都研究了与瞬变流相关的检测方法。通过控制管道末端阀门周期性的开关或瞬间全部关闭产生瞬变流动的方法，虽然能够检测到微小的泄漏，但是对阀门的控制要求高，投资大，阀门的瞬间快速关闭会产生较高的压力突变，也是不符合安全生产运行要求的。郭新蕾、杨开林、王通等采用的阀门小开度快速关闭的方法提高了阀门的可操作性和安全性，因此本文在仿真实验中，采用了阀门小开度快速关闭的方法。

Wang Xiaojian[4]等人利用阀门突然关闭产生瞬变流，根据压力波各个谐波分量在无泄漏和有泄漏时衰减程度的不同，通过计算压力波不同谐波分量的泄漏衰减率之比来确定泄漏位置。各次谐波的衰减率通过将压力波信号截取出不同的周期，对每个周期分别做傅里叶变换计算出不同谐波的归一化幅值，再对各次谐波不同周期的归一化幅值进行指数拟合计算。由于计算过程中压力波信号的周期不易准确获得，影响到了衰减率计算的准确性，从而影响了泄漏的定位精度，并且计算过程比较复杂，影响定位的速度。本文提出利用短时傅里叶变换的方法对压力波信号进行时频分析，获得不同频率的信号归一化幅值随着时间的变化规律，在所得的结果中提取出压力波信号的不同谐波分量，通过指数拟合得到不同谐波分量的衰减率，这种方法能够更加精确地计算出各谐波分量的衰减率，从而提高了定位精度。

2 瞬变流检测的定位方法

利用瞬变流对管道泄漏进行检测和定位的方法整体流程如下：

（1）在管道中引入瞬变流，通过控制管道末端的阀门小开度快速部分关闭，使管道内压力发生瞬态变化。

（2）对采集到的压力信号进行分析，计算信号中不同谐波的衰减率。衰减率准确与否直接影响到管道的定位精度。

（3）对计算的衰减率进行分析，根据泄漏的定位公式对泄漏进行定位。

计算压力信号的衰减率，传统的周期分析方法是将压力波划分为不同的周期，如图1 所示，对每个周期分别进行傅里叶变换分解得到一系列谐波分量，则第n个谐波分量在第i个周期的幅值表示为[4]：

式中T*=T/(L/a)为无量纲的管道压力瞬变信号的周期，其中T为压力波信号的周期，L为管道长度，a为压力波波速；R为管道摩擦产生的衰减系数；RnL为管道泄漏产生的泄漏衰减系数。

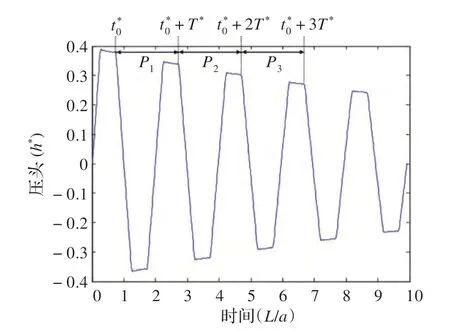
图1 管道瞬态信号划分不同周期的示意图

通过式（1）对各谐波分量在不同周期的幅值进行拟合，得到各谐波分量的衰减系数。当管道没有泄漏时，各谐波分量均以相同的摩擦衰减系数呈指数衰减。当管道存在泄漏时，对于不同的谐波分量n,由管道泄漏引起的泄漏衰减系数RnL则各不相同。当管道存在泄漏时，根据采集到的阀门动作后的瞬态信号，通过计算得到各谐波分量幅值的衰减率R+RnL。用R+RnL减去无泄漏时管道摩擦引起的衰减系数R即得到泄漏衰减率RnL。设一对谐波分量n=n1和n2,则两个谐波分量泄漏衰减率之间的比值为：

图2 给出了不同谐波分量的泄漏衰减率比值对于不同泄漏点位置的响应。从图2 可以看出，每个R2L/R1L值，除了在xL*=0.5 外，都对应着两个泄漏点的位置。对于更高次谐波分量的衰减率的比值将对应着更多泄漏点的位置，所以本文只选取基波、二次谐波和三次谐波分量来对管道泄漏进行定位。计算结果会得到两个对称的泄漏点位置，但是仍可满足工程实际的基本要求，本文旨在提高泄漏点定位的精度，对于多值问题此处不做讨论。由公式（2）可知要想提高泄漏的定位精度就要更加准确地计算得到不同谐波分量的泄漏衰减系数RnL,因此需要更加准确地提取出瞬变压力波信号中的各谐波分量并计算其衰减系数。

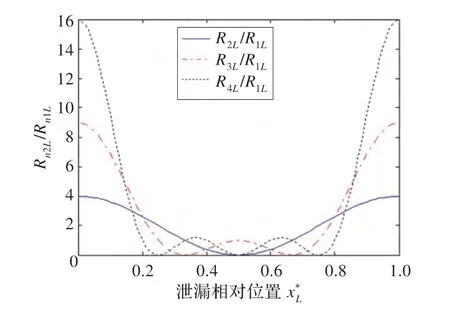
图2 不同谐波分量泄漏衰减率比值对于不同泄漏位置的响应

3 时频分析的谐波提取方法

时频分析[13-14]是非平稳信号处理的一个重要分支，它利用时间和频率的联合函数来表示非平稳信号，并对其进行分析和处理。时频分析方法根据时频联合函数的不同可以分为线性时频表示和双线性时频表示。典型的线性时频表示有短时傅里叶变换（STFT），典型的双线性时频表示有Wigner-Ville 分布（WVD）。WVD 能够描述信号的能量在时域和频域中的分布，其最主要的缺陷就是存在交叉干扰项，干扰项一般是振荡的，而且幅度可以达到自主项的两倍之多，造成信号的时频特征模糊。STFT 能够有效地描述信号的局部特征，并且它本身不存在交叉项的干扰，适用于多分量的分析。本文主要分析信号中不同谐波各自随时间的变化规律，不希望有干扰项的影响，因此选择STFT 对压力信号进行分析，观察不同谐波分量随时间的变化规律。

短时傅里叶变换是通过给定一个时间宽度很短的窗函数η(t),让它沿信号z(τ)滑动从而使信号逐段进入被分析的状态，可以得到一个时变的频率分析结果。信号z(τ)的短时傅里叶变换定义为：

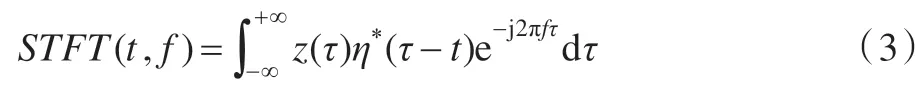
式中*指复数的共轭。

管道内的压力瞬变也是一种非平稳信号，利用短时傅里叶变换研究压力瞬变的时频特性，从中提取出需要的特定频率信号，即压力瞬变信号的基波、二次谐波和三次谐波分量的归一化幅值。根据公式（1）可以推导出第n次谐波分量的归一化幅值An随着时间t的变化规律：

其中Kn为n次谐波分量的系数。根据公式（4）分别对这三个频率信号的归一化幅值进行指数拟合计算得到衰减率。分别计算有泄漏和无泄漏时各谐波衰减率的值，再根据公式（2）对泄漏进行定位。

4 仿真实验与结果分析

4.1 仿真实验

为了检验时频分析法能够准确计算各次谐波的衰减系数，提高泄漏的定位精度，用Flowmaster 软件[15]对管道的泄漏情况及阀门的动作进行了仿真计算。图3为建立的管道模型。为了尽量模拟真实的管道环境，在系统建模时均采用弹性管道，管道长L=100 m,口径D=40 m,管道内壁粗糙度ε=0.025 mm,首末端分别是水深50 m 和2 m 的恒压水箱，压力波波速a=1 000 m/s。在管道70 m 处设有一个球阀，通过连接控制器对它输入控制信号来控制阀门的开度。在管道40 m 的位置上通过连接一段极细的管道来模拟泄漏，泄漏孔径分别选取3 mm 和1 mm 做泄漏仿真。泄漏孔为3 mm 时泄漏流量约占总流量的2.7%，泄漏孔为1 mm 时泄漏流量约占总流量的0.17%。仿真的时间间隔均为0.001 s。

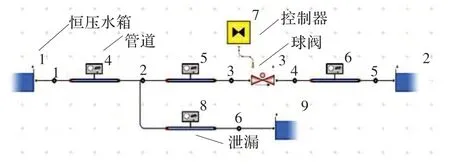
图3 仿真管道模型

控制阀门在0.05 s 内小开度快速关闭，分别测得管道无泄漏和两种不同泄漏时阀门处的压力信号，如图4（a）所示，压力波幅值在有泄漏存在时幅值较小且衰减比较迅速，泄漏孔径越大衰减越明显。经过理论计算，信号的周期应该为T=2×L/a=0.2 s。图4（b）为无泄漏时压力波信号的频谱图，可以看出前三次谐波的频率分别为5 Hz、10 Hz和15 Hz，与理论值相符。

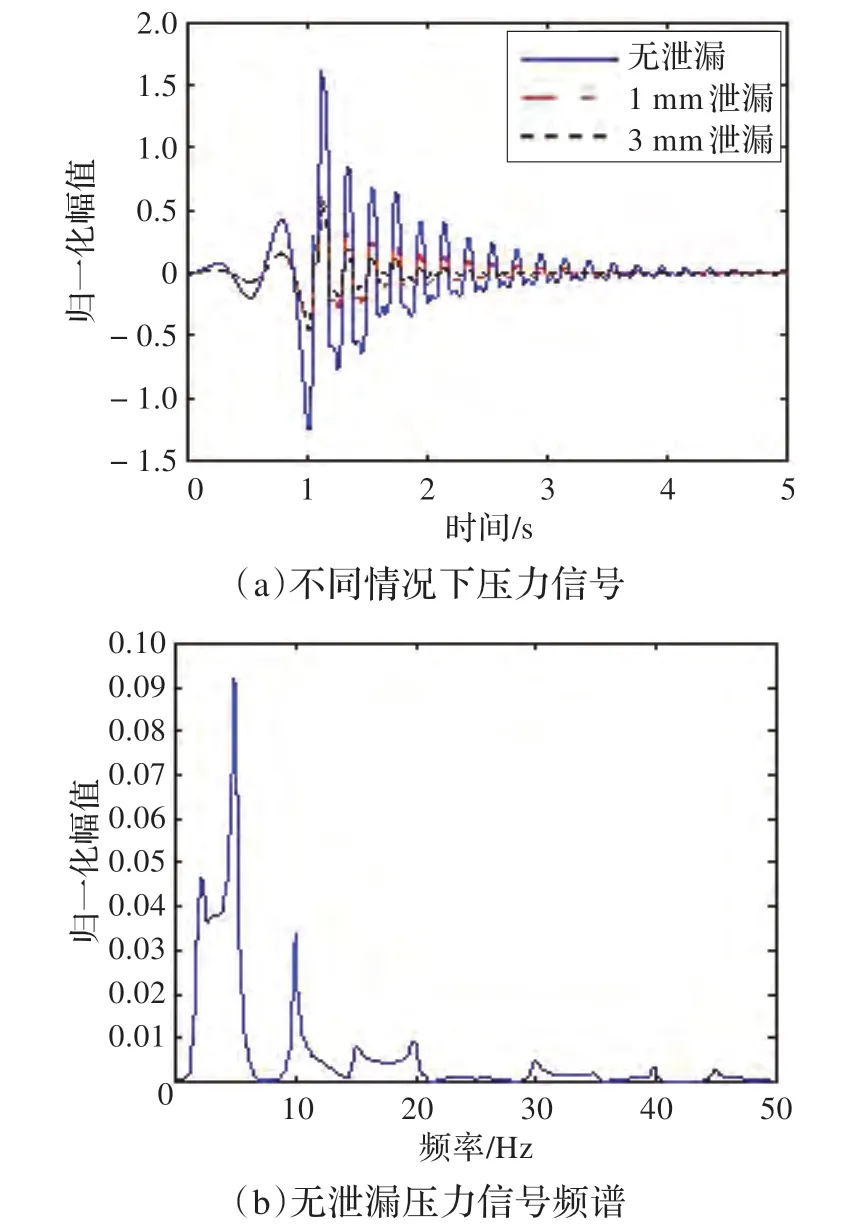
图4 不同情况下压力波信号及频谱

4.2 周期分析法

将在管道内采集到的瞬态信号划分为不同周期，对每个周期的信号分别作傅里叶变换得到各谐波的幅值，根据各个谐波分量在不同周期的幅值变化利用公式（1）求得其拟合曲线，图5 表示了无泄漏和有泄漏时每个周期各次谐波的幅值和拟合曲线。

求得的各谐波分量的衰减率见表1。仿真实验中通过计算得到的管道没有泄漏时各次谐波的衰减率均不相同，这是由于非稳态因素的影响。当管道内流体处于定常流状态时，管道参数不随时间变化，可以得到稳态衰减系数；当阀门动作流体处于瞬变状态时，管道内部作用力变得不规则，因而产生非稳态磨阻。非稳态摩阻对不同谐波衰减的影响是不同的，因此没有泄漏时不同谐波的衰减率也不相同。在无泄漏和有泄漏的实验中，稳态流动的状态是一致的并且由于每次实验中阀门都是在相同的位置以几乎相同的速度相同的动作关闭，因此由阀门动作引入的瞬变流动也是一致的，所以在实验中除了泄漏的影响，各次谐波在有泄漏和无泄漏时的衰减率是一致的。因此通过做差即可得到由于管道泄漏产生的衰减系数。计算衰减率R2L和R1L,R3L和R1L的比值利用公式（2）得到泄漏的相对位置，计算结果如表2所示。所以当管道存在1 mm孔径的泄漏时，定位的结果是39.12 m；管道存在3 mm泄漏时，定位的结果是38.91 m。

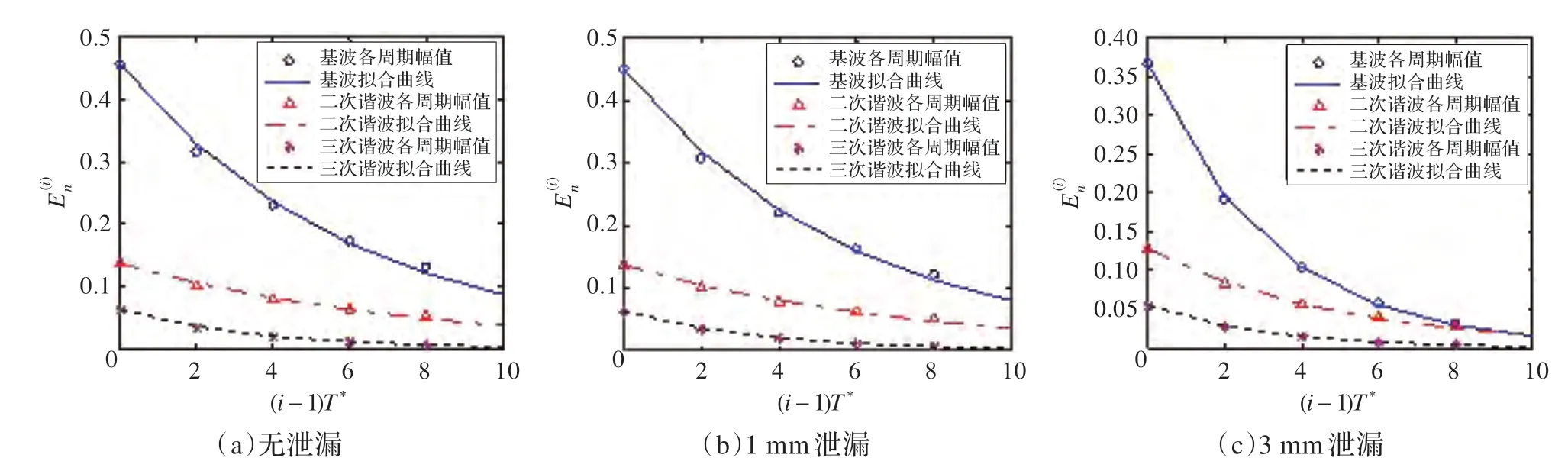
图5 无泄漏和有泄漏时谐波信号各周期幅值及拟合曲线

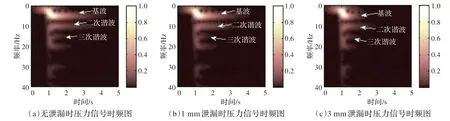
图6 无泄漏和有泄漏时压力信号的时频分析图

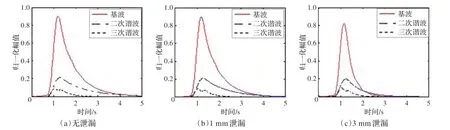
图7 无泄漏和有泄漏时基波、二次谐波和三次谐波能量分布图

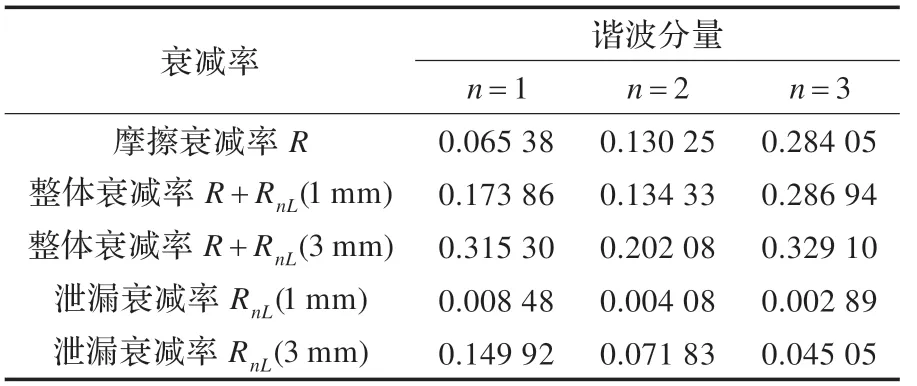
表1 周期分析各谐波分量的衰减率计算结果

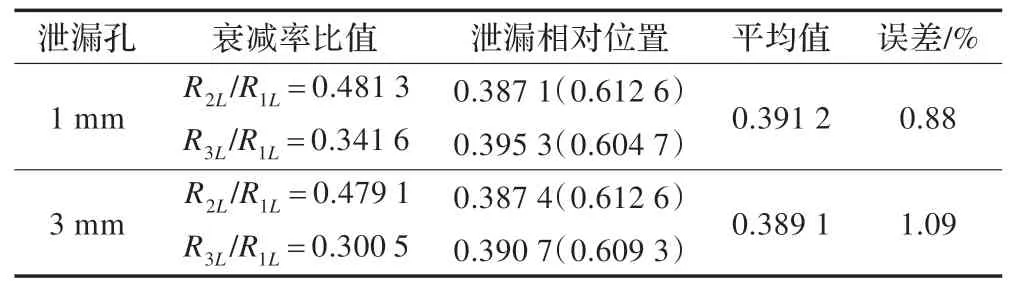
表2 周期分析定位结果及误差

4.3 时频分析与泄漏定位

在用短时傅里叶变换对压力波信号做时频分析时，选择汉明窗和合适的窗长。如图6，纵坐标指不同频率的信号，横坐标指不同频率信号随时间的变化规律，颜色深浅表示信号在时频面上的归一化幅值分布情况。所得结果既可以比较清晰地区分开三个频率的信号，又不影响分析信号归一化幅值随时间的变化规律。

在时频分析所得的结果中提取出三个频率信号的归一化幅值，观察它们的时域特性。如图7 中分别是无泄漏和有泄漏时基波、二次谐波和三次谐波分量的归一化幅值随时间的变化规律。三个图对比可以看出有泄漏时各谐波分量的归一化幅值比无泄漏时各谐波分量的归一化幅值衰减要迅速，这是由于泄漏的存在产生了能量损失，并加快了压力波幅值的衰减。由于1 mm孔径时泄漏量比较小，因此图中不容易直接看出衰减率的增加。

对无泄漏时基波信号的归一化幅值，选取从峰值处开始到第5 s 之间的数据根据公式（4）做指数拟合运算，得到拟合曲线：A1=4.648 3×e-1.3536×t,则其衰减率为0.135 36。拟合的确定系数R-square=0.998 8。拟合的确定系数越接近1，表明拟合曲线对原始曲线的解释能力越强，因此拟合曲线对数据拟合的也较好。图8 为无泄漏时基波信号的归一化幅值及拟合曲线。同理可以求得无泄漏时二次谐波和三次谐波分量以及两种有泄漏情况下的基波、二次谐波和三次谐波分量归一化幅值的衰减率，结果如表3 所示。

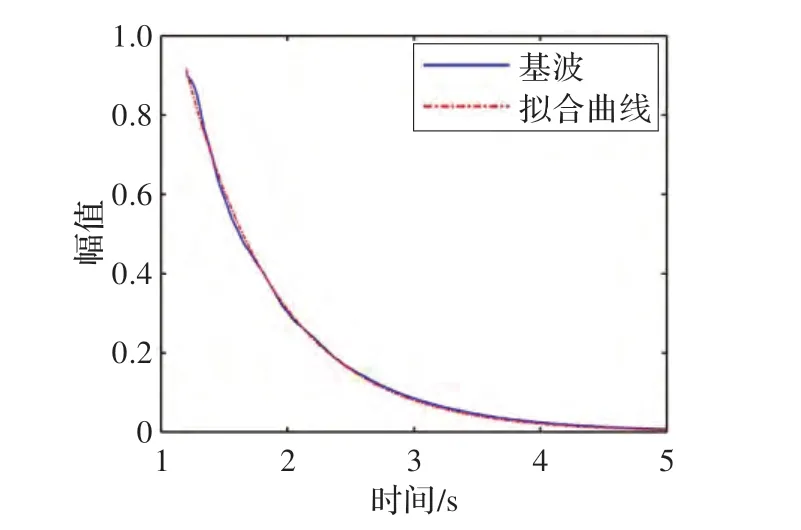
图8 无泄漏时基波信号及其指数拟合曲线

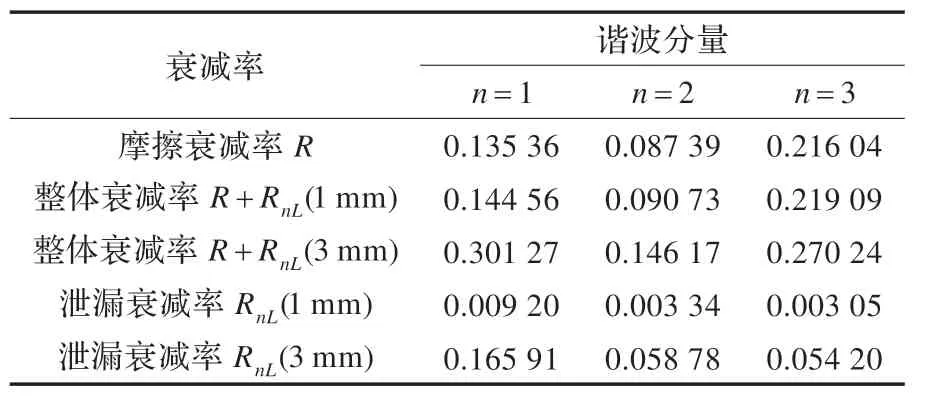
表3 时频分析法各谐波分量的衰减率计算结果

计算衰减率R2L和R1L,R3L和R1L的比值，根据公式（2）得到泄漏的相对位置，计算结果如表4所示。当管道存在1 mm孔径的泄漏时，定位的结果是39.85 m；管道存在3 mm 泄漏时，定位的结果是39.89 m。可见当管道存在微小泄漏时，该方法仍能够准确地对泄漏进行定位。由此可以看出用时频分析法提取的各谐波分量的幅值经过指数拟合后得到的衰减率更准确，定位精度更高。

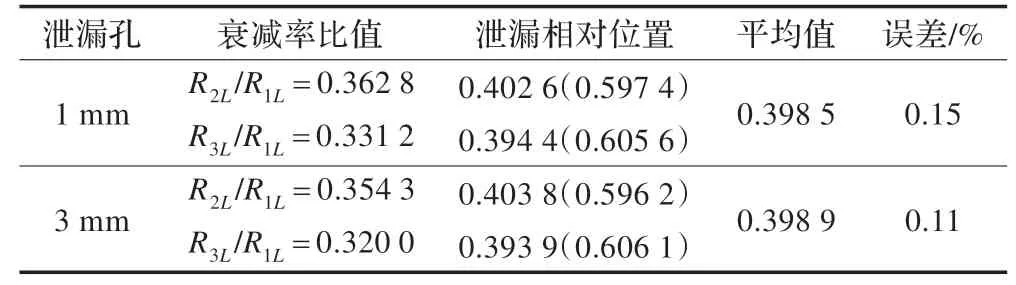
表4 时频分析法定位结果及误差

5 结束语

本文用Flowmaster 流体仿真软件建立了管道模型，通过控制阀门小开度快速关闭，使管道内部产生瞬变流动，对管道无泄漏及1 mm 和3 mm 两种不同大小孔径的泄漏进行了仿真计算，得到三种情况下阀门动作后的压力波信号。

采用短时傅里叶变换对压力波信号进行时频分析，更容易理解不同频率信号的归一化幅值随时间的变化规律。对得到的特定频率的信号进行指数拟合计算，与分别计算信号每个周期各谐波分量的归一化幅值再对各谐波分量归一化幅值进行指数拟合计算相比，能够更加快速和准确地得到各个谐波分量的衰减率，从而减少了定位所需的时间，提高了定位的精度，对于0.17%的微小泄漏也能够准确定位。

[1] Mpesha W，Sarah L G，Chaudhry M H.Leak detection in pipes by frequency response method[J].Journal of Hydraulic Engineering，2001，127：134-147.

[2] Ferrante M，Btunone B.Pipe system diagnosis and leak detection by unsteady state tests 1.harmonic analysis[J].Advances in Water Resources，2003，26：95-105.

[3] Ferrante M，Btunone B，Meniconi S.Wavelets for the analysis of transient pressure signals for leak detection[J].Journal of Hydraulic Engineering，2007，133（11）：1274-1282.

[4] Wang X J，Lambert M F，Simpson A R，et al.Leak detection in pipeline systems using the damping of fluid transients[J].Journal of Hydraulic Engineering，2002，128（7）：697-711.

[5] Wang X J，Simpson A R，Lambert M F.An analytical solution for the transient in a pipeline with variable boundary condition：leak detection in pipe networks using coded transient[C]//Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium，Cincinnati，Ohio，USA，2006.

[6] 郭新蕾，杨开林，郭永鑫，等.管道泄漏检测全频域法试验验证及抗噪性研究[J].水利学报，2011，42（6）：713-720.

[7] 郭新蕾，杨开林，郭永鑫，等.管道系统泄漏检测的瞬变水击压力波法[J].应用基础与工程科学学报，2011，19（1）：20-28.

[8] Guo Xinlei，Yang Kailin，Li Futian，et al.Analysis of first transient pressure oscillation for leak detection in a single pipeline[J].Journal of Hydrodynamic，2012，24（3）：363-370.

[9] 王通，阎祥安，李伟华.基于谐波分析的输油管道泄漏检测机理研究[J].化工自动化及仪表，2005，32（1）：51-54.

[10] 王通，阎祥安，李伟华，等.基于激励响应的输油管道泄漏检测技术研究[J].化工自动化及仪表，2006，33（1）：59-63.

[11] 白莉，岳前进，李洪升.基于水力瞬变与扩展卡尔曼滤波的管道流态监测与泄漏定位[J].计算力学学报，2005，22（6）：739-744.

[12] 伍悦宾，刘天顺.基于瞬变反问题分析的给水管网漏失数值模拟[J].哈尔滨工业大学学报，2005，37（11）：1483-1485.

[13] 葛哲学，陈仲生.Matlab 时频分析技术及其应用[M].北京：人民邮电出版社，2006.

[14] 唐向宏，李齐良.时频分析与小波变换[M].北京：科学出版社，2008.

[15] 张宇.输油管道泄漏检测新方法与关键技术研究[D].天津：天津大学，2009.