CDC-代数上中心化子的刻画
马 飞,张建华,尹琳娟
MA Fei1,ZHANG Jianhua2,YIN Linjuan1
1.咸阳师范学院 数学与信息科学学院,陕西 咸阳712000
2.陕西师范大学 数学与信息科学学院,西安710062
1.College of Mathematics and Information Science,Xianyang Normal University,Xianyang,Shaanxi 712000,China
2.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China
1 引言
设A是一个环或代数,如果对任意的a,b∈A,aAb={0}蕴涵a=0 或b=0,那么称A是素的;如果aAa={0}蕴涵a=0,那么称A是半素的。如果可加映射φ:A→A满足对任意的a,b∈A有φ(ab)=φ(a)b(φ(ab)=aφ(b)),那么称φ是一个左(右)中心化子;如果有φ(a2)=φ(a)a(φ(a2)=aφ(a))成立,那么称φ是一个左(右)Jordan 中心化子。如果φ既是左中心化子又是右中心化子,那么称φ是中心化子。与中心化子密切相关的一类重要映射是中心化映射:若映射φ:A→A满足对任意的a∈A,有φ(a)a-aφ(a)∈Z(A)(Z(A)为A的中心),则称映射φ是中心化的;特别的,若φ(a)a=aφ(a),则称映射φ是可交换的。
关于中心化子的研究一直深受研究人员的关注。如Beidar[1]证明了若半素环R上的映射φ既是左Jordan中心化子,又是右Jordan 中心化子,则存在环R的扩展中心中的元素λ,使得φ(a)=λa对任意的a∈R都成立;Vukman[2]对2-非扰自由半素环R上的可加映射φ证明了,如果对任意的a∈R,有2φ(a2)=φ(a)a+aφ(a),那么φ是中心化子;Zalar[3]证明2-非挠的半素环上的任意的左(右)Jordan 中心化子是左(右)中心化子;Benkovič和Eremita[4]证明2-非挠的素环上的可加映射φ如果满足对任意的a∈R,n≥2 都有φ(an)=φ(a)an-1,那么φ是左 中 心 化 子;Vukman[5]推 广Benkovič 和Eremita 的 结论,证明在标准算子代数A上,若可加映射φ满足对任意的a∈A,有φ(am+n+1)=amφ(a)an(其中m、n为正整数),则存在数域F中的常数λ,使得对任意的a∈A,有φ(a)=λa。杨[6]将Vukman 的结果推广到了套代数上,证明了在套代数上的可加映射φ若满足(m+n)φ(ar+1)=mφ(a)ar+narφ(a)(也 称 为 广 义Jordan 中 心 化 子)或φ(am+n+1)=amφ(a)an,则存在数域F中的常数λ,使得对任意的a∈A,有φ(a)=λa。文献[7]证明:设T是一个三角代数,如果一个可加映射φ:T→T满足,对任意的a∈T,有(m+n)φ(ar+1)-mφ(a)ar-narφ(a)∈Z(T)或φ(am+n+1)-amφ(a)an∈Z(T) 成 立( 其 中m,n,r为 正 整数),那么存在T的中心中的元素λ∈Z(T),使得对任意的a∈T,有φ(a)=λa。类似结果可见文[8-10]。
设H是一个复可分的Hilbert 空间,L是H上的子空间格。其子空间格代数为AlgL={T∈B(H):T(l)⊆L,∀l∈L}。如果一个子空间格L中的任意两个投影是可交换的,则称L是交换子空间格,简称CSL,相应的称AlgL为CSL 代数。一个全序子空间格N称为套,相应的代数AlgN称为套代数。若∀0 ≠e∈L,有e= ∨{l∈L:l⊄N-},则称CSL 是完全分配格,其中N-= ∨{P∈L:N⊄P},相应的称完全分配格的CSL 代数为CDC-代数。本文主要讨论具有完全分配交换子空间格的代数,关于完全分配格代数的标准定义见文献[11-12]。显然,套是完全分配的交换子空间格,也是其最重要的模型。
由文献[13]可知,CDC-代数是由其包含的秩一算子弱*闭生成的算子代数,这个结果对研究CDC-代数具有重要的意义;文献[14-15]分别研究了CDC-代数上的代数同构、线性导子及线性Lie 导子。在CDC-代数AlgL中,记U(L)={e∈L:e≠0,e-≠H}, 称U(L) 中 的e,e′是连通的,如果存在e1,e2,…,en∈U(L),使得ei与ei+1可比,e0=e,en+1=e′(i=0,1,…,n)。设C⊆U(L),如果C中任意两个元素是连通的,并且C中的任何元素与U(L)C中的元素都不连通,那么称C是U(L)的一个连通分支。设L是复可分的Hilbert 空间H上的一个完全分配的交换子空间格,由文献[16]可知,AlgL是不可约的,当且仅当其交换子是平凡的,即其一次换位是FI,也等价于L∩L⊥={0,I},其中L⊥={e⊥:e∈L}。显然,套代数是一个不可约的CDC-代数。受中心化子和中心化映射及上述结论的启发,本文主要证明:CDC-代数AlgL上的可加映射φ,如果满足对任意的正整数m,n≥1 和a∈AlgL,有φ(am+n+1)=amφ(a)an,那么存在λ∈Z(AlgL),使得对任意的a∈AlgL,有φ(a)=λa(见定理2.1)。
2 主要结果及证明
本文的主要结论如下:
定理2.1设AlgL是Hilbert空间H上的CDC-代数,φ:AlgL→AlgL是一可加映射。若存在正整数m,n≥1,使得对于任意a∈AlgL,有:

则存在Z(AlgL) 中的常数λ,使得对任意的a∈AlgL,有φ(a)=λa。
为了证明这个结论,首先考虑在不可约CDC-代数上的情形。在不可约CDC-代数上,文献[14]证明了下面的结论。
引理2.1[14]设AlgL是Hilbert 空间H上的不可约CDC-代数,则存在一个非平凡投影e∈L,使得e(AlgL)e⊥是忠实的AlgL-双边模。这里忠实的AlgL-双边模指的是对于任意的a∈AlgL,若ae(AlgL)e⊥={0},则有ae=0;若e(AlgL)e⊥a={0},则有e⊥a=0。
为了证明定理2.2,需要证明下面的结论:
引理2.2设AlgL是Hilbert 空间H上的不可约CDC-代数,φ:AlgL→AlgL是一可加映射。若存在正整数m,n≥1,使得对于任意a∈AlgL,有:

则存在数域F中的常数λ,使得对任意的a∈AlgL,有φ(a)=λa。
证明若L={0,H},即L只有平凡投影,则AlgL=B(H是素的,则由文献[10]的主要结论可知,存在数域F中的常数λ,使得对任意的A∈AlgL,有φ(a)=λa。
下面假设L是非平凡的。由引理2.1 可知,存在非平凡投影e∈L,使得e(AlgL)e⊥是忠实的AlgL-双边模。令e1=e,e2=I-e,则e1,e2∈AlgL且均为投影。则对于任意的a∈AlgL可分解为:
a=e1ae1+e1ae2+e2ae2
因而可将AlgL代数分解为:
AlgL=A11⊕A12⊕A22
其中Aij=ei(AlgL)ej。
在式(2)中用a+b代替a可得:
(m+n)φ(ab+ba)=mφ(a)b+naφ(b)+
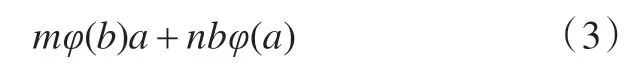
特别的,在式(3)中令b=I,则有:

下面分三个步骤来完成本引理的证明。
结论1对于任意aij,bij∈Aij,有φ(Aij)⊆Aij(1 ≤i≤j≤2)。
由φ满足式(2)可得:
(m+n)φ(ei)=mφ(ei)ei+neiφ(ei)
上式两边分别左乘和右乘ei,则对于i=1,2,有:

又因为(m+n)φ(ei)=mφ(I)ei+neiφ(I)。对上式两边分别左乘和右乘ei,可得:

对任意aii∈Aii(i=1,2),由式(3)可知:
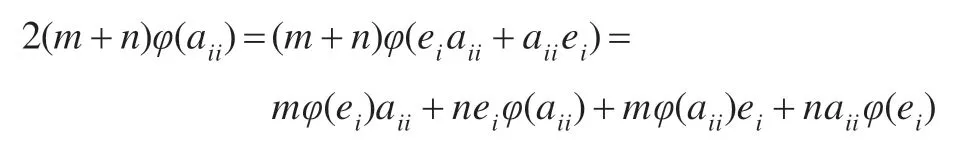
对上式两边左乘和右乘ei,且由式(6)可知:eiφ(aii),φ(aii)ei∈Aii,即φ(aii)=eiφ(aii)ei∈Aii。
对任意a12∈A12,由式(4)可知:
(m+n)φ(a12)=mφ(I)a12+na12φ(I)
对上式两边分别左乘e2和右乘e1,则有:
(m+n)e2φ(a12)=me2φ(I)a12=mφ(I)e2a12=0
及 (m+n)φ(a12)e1=na12φ(I)e1=na12e1φ(I)=0
因而有φ(a12)e1=e2φ(a12)=0。即φ(a12)=e1φ(a12)=φ(a12)e2=e1φ(a12)e2∈A12。
结论2对于任意的aij,bij∈Aij,有:
(1)φ(a11b12)=φ(a11)b12=a11φ(b12)
φ(a12b22)=φ(a12)b22=a12φ(b22)
(2)φ(a11b11)=φ(a11)b11=a11φ(b11)
φ(a22b22)=φ(a22)b22=a22φ(b22)
由式(2)、(3)及结论1 可知,对任意的a11∈A11,b12∈A12有:

在上式中取a11=e1,有:
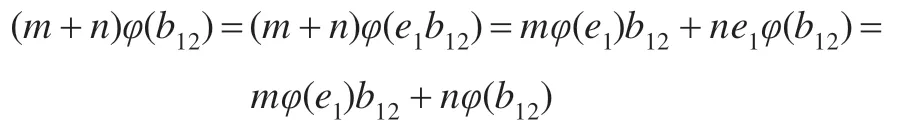
即φ(b12)=φ(e1)b12。
同理可证:φ(a12)=a12φ(e2)。从而有:
φ(a11b12)=a11b12φ(e2)=a11φ(b12)
和φ(a11b12)=φ(e1)a11b12=φ(a11)b12
类似可得:

对任意的a12∈A12,由式(7)可知:
φ(a11b11)a12=φ(a11b11a12)=φ(a11)b11a12
且φ(a11b11)a12=φ(a11b11a12)=a11φ(b11a12)=a11φ(b11)a12
在不可约CDC-代数中,由e(AlgL)e⊥是忠实的AlgL-双边模,因而A12是忠实的(A11,A22)-双模,因而有:
φ(a11b11)=φ(a11)b11=a11φ(b11)
对任意的a12∈A12,由式(8)可知,a12φ(a22b22)=φ(a12a22b22) =a12a22φ(b22) 且a12φ(a22b22) =φ(a12a22b22) =φ(a12a22)b22=a12φ(a22)b22。因而有:
φ(a22b22)=φ(a22)b22=a22φ(b22)
结论3对于任意的a∈A,有φ(a)=λa。
对于任意的a,b∈AlgL,则存在aij,bij∈Aij,使得:a=a11⊕a12⊕a22,b=b11⊕b12⊕b22。
由结论1 和结论2 可知:

上式中取B=I可得对任意的A∈AlgL有φ(A)=φ(I)A=Aφ(I)。因为在AlgL中其换位子是平凡的,即(AlgL)′=FI因而存在λ∈F,使得φ(I)=λI,从而对任意A∈A,有φ(A)=λA。
定理2.2 的证明在式(1)中用a+tI代替a(其中为数域F中的任意数),由φ的可加性得:

由t的任意性可知,对于任意的t的i次方,式(9)都成立。特别的,当t的次方为m+n-1 时,由等式两边系数相等可得:

当t的次方为m+n时,由等式两边系数相等可得:
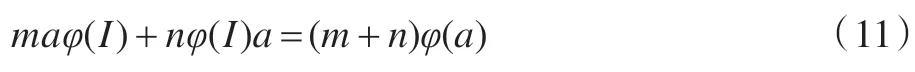
对式(10)两边左乘和右乘A可得:

上两式相加得:

在式(11)中用a2代替a,得:
ma2φ(I)+nφ(I)a2=(m+n)φ(a2)
比较上两式可知:
(m+n)aφ(I)a=(m+n)(φ(a)a+aφ(a))-(m+n)φ(a2)
将式(14)带入式(12)与(13)可得:

将aφ(I)a,a2φ(I)及φ(I)a2带入式(10),从而得到一个关于aφ(a),φ(a)a及φ(a2)的等式:
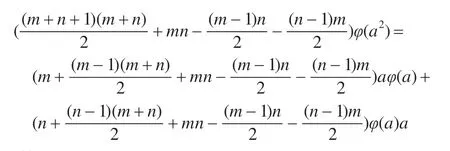
化简得:
(m+n)φ(a2)=maφ(a)+nφ(a)a
即φ满足式(2)。由引理2.2 知,存在λ∈F,使得对任意a∈AlgL,有φ(a)=λa。
Gilfeather 和Moore 在文献[16]中证明了任何一个CDC-代数都可以分解成可数个不可约CDC-代数的直和,这个结果在研究CDC-代数的同构和导子等时具有非常重要的作用,下面给出这个结论。

定 理2.1 的 证 明设en=∨{e:e∈Cn,n∈Λ} 为 引 理2.3 所述的投影,则有:

并且显然有:
(AlgL)en=en(AlgL)en=Alg(enL)
因为en=∨{e:e∈Cn,n∈Λ}是Hilbert空间H上的投影,因此,其也是Hilbert空间。因而,(AlgL)en是Hilbert空间en上的不可约CDC-代数,并且这里的收敛指的是强收敛。由引理2.3 中的en的定义可知,其线性张的闭包就是Hilbert 空间H,并且{en,n∈Λ}⊆L∩L⊥两两正交,因而有∑en=I为AlgL的单位元。
对于任意的a∈AlgL和任意的n,由φ满足式(1),因而取a=en可得:
φ(en)=enφ(en)en
分别左右乘en,有:
φ(en)=enφ(en)en=enφ(en)=φ(en)en
又因为(AlgL)en是en上的不可约CDC-代数,从而由引理2.2 的证明可知,φ满足式(3),从而有:

结合引理2.2 的第一步,可得:

所以有:
φ(enaen)=enφ(enaen)en
设在Alg(enL) 上有φ=φn,即φn为φ在Alg(enL上的限制,则有φn:Alg(enL)→Alg(enL) 是可加映射并且在Alg(enL)=(AlgL)en=en(AlgL)en上满足引理2.2,则由引理2.2 知,对于任意的a∈Alg(enL),存在λ∈F,使得φn(a)=λa。
设an,a∈AlgL,an是强收敛于a的,则对于任意的H中的x,结合引理2.2的证明可知φ满足式(4),因而有:


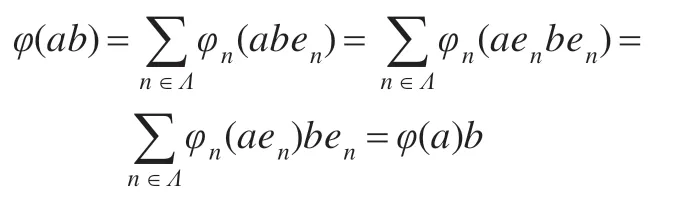
从而,对于任意的a∈AlgL,有:
φ(a)=φ(I)a=aφ(I)
即φ(I)∈Z(AlgL),因 而 存 在λ=φ(I)∈Z(AlgL), 使 得φ(a)=λa。
通过定理2.1 的证明过程,很容易得到下面的推论。
推论2.1设AlgL是Hilbert空间H上的CDC-代数,φ:AlgL→AlgL是一可加映射,则下面几个条件等价。
(1)存在λ∈Z(AlgL),使得对任意a∈AlgL,有φ(a)=λa。
(2)存在正整数m,n,使得对任意的a∈AlgL,有:φ(am+n+1)=amφ(a)an。
(3)对任意的正整数m,n,r和任意的a∈AlgL,有:φ(am+n+1)=amφ(a)an。
(4)φ:AlgL→AlgL是中心化子。
3 结论
本文主要研究了CDC-代数AlgL上的满足φ(am+n+1)=amφ(a)an可加映射φ,有φ(a)=λa(其中λ∈Z(AlgL))的固定形式,给出了CDC-代数上的保持映射的刻画,具有一定的理论意义。
[1] Brešar M.Centralizing mappings on von Neumann alge bras[J].Proc Amer Math Soc,1991,3:501-510.
[2] Vukman J,Kosi-Ulbl I.On centralizers of semiprime rings[J]Aequationes Math,2003,66:277-283.
[3] Zalar B.On centralizers of semiprime rings[J].Comment Math Univ Carolin,1991,32:609-614.
[4] Benkovič D,Eremita D.Characterizing left centralizers by their action on a polynomial[J].Publ Math Debrecen,2004,64(3):343-351.
[5] Vukman J,Kosi-ulbl I.Centralizers rings and algebras[J].Bull Austral Math Soc,2005,71:225-234.
[6] 杨翠,张建华.套代数上的广义Jordan 中心化子[J].数学学报,2010,53(5):975-980.
[7] 马飞,张建华,李莉,等.三角代数上中心化子的刻画[J].计算机工程与应用,2013,49(15):23-26.
[8] 李倩,李鹏同.完全分配CSL 代数上的中心化子[J].数学年刊,2011,32(3):375-384.
[9] Qi X F.Characterization of Centralizers and Generalized derivations on J- subspace lattice algebras[J].Acta Math Scientia,2014,34(2):463-472.
[10] 马飞,张建华.标准算子代数上中心化子的刻画[J].山大大学学报:理学版,2014,48(9):64-68.
[11] Hopenwasser A.Complete distributivity[J].Proc Sym Pure Math,1983,119:227-240.
[12] Lambrou M S.Complete distributivity lattices[J].Fundamenta Math,1990,51:285-305.
[13] Laurie C,Longstaff W.A note on rank-one operators in reflexive algebras[J].Proc Amer Math Soc,1983,89(2):293-297.
[14] Lu F.Derivations of CDC algebras[J].J Math Anal Appl,2006,323(1):179-189.
[15] Lu F.Lie derivations of certain CSL algebras[J].Israel J Math,2006,155:149-156.
[16] Gilfeather F,Moore R L.Isomorphisms of certain CSL algebras[J].J Funct Anal,1986,67:264-291.

