蚁群优化小波阈值算法用于变电设备状态信号提取

龙虹毓 张晓勇 胡晓锐 冯姗姗 李 龙

蚁群优化小波阈值算法用于变电设备状态信号提取

龙虹毓1张晓勇2胡晓锐2冯姗姗3李 龙2

（1. 西南大学工程技术学院 重庆 400715 2. 国网重庆市电力公司电力科学研究院 重庆 401123 3. 浙江杭州余杭供电局 杭州 311100）

针对变电设备状态信号的快速有效提取，降低去噪信号的畸变率，本文提出了一种用于电气设备状态信号去噪的蚁群优化小波阈值算法。该方法在计算最优阈值时，采用基于SURE无偏估计的最优阈值选择方法，结合蚁群优化算法进行全局自适应搜索最优阈值，大大提高了最优阈值自适应寻优速度。为了验证其去噪效果，本文还引进标准软阈值法及梯度迭代优化小波阈值方法对两种典型人工平稳信号、局部放电模拟信号及实测局部放电工频信号进行去噪，结果表明本文提出的方法比其他两种方法的去噪效果更优，计算速度更快，具有良好的去噪效果和应用价值。

变电设备 带电检测 状态信号 小波去噪 蚁群优化算法

1 引言

在智能电网规划的推动下，未来数字化变电站将成为新建变电站的主流。数字化变电站的建立有利于实现电网的科学化管理与决策，有助于改善电力系统的安全稳定性[1-2]。电网信号量极多且信号检测、传输的电磁环境恶劣，这给信号提取和实时监测带来了很大的麻烦。此外，诸如局部放电信号等非平稳信号的快速有效提取，更是给电气设备的带电检测及在线监测技术的推广提出了考验[3]。

近年来，多种抗干扰数字化去噪方法已应用于电气设备的状态信号处理中，文献[4]提出了采用级联去噪方法处理局部放电信号，首先采用数字滤波器[5-6]抑制窄带周期性干扰，然后采用小波去噪法[7-10]去除白噪声，最后通过脉冲序列分析方法[11]或者人工智能方法[12]可以有效抑制脉冲干扰，但前提是去除白噪声并获取畸变率小的脉冲序列。因此，小波阈值的最优选择对提取有效的局部放电信号具有重要的意义。

文献[13]提出了软阈值及硬阈值法，并提出了基于SURE的阈值选择方法。文献[14]在SURE阈值选择方法基础上提出了一种梯度迭代优化小波阈值方法，与基于SURE的阈值估计方法相比，该方法针对平稳信号中的白噪声具有更好的抑制效果。但其计算时间花费大，为了实现数字化信号的快速传输，信号处理需要快速化。此外，梯度迭代优化小波阈值方法用于非平稳信号（如局部放电信号）去噪时，计算不易收敛，难以实际用于电气设备状态信号的快速有效提取[15]。文献[10]提出了粒子群算法对小波阈值的选择进行优化，试验结果表明该种方法比文献[14]提出的方法大大缩减计算时间，减小去噪信号畸变，但其处理离散优化问题易陷入局部最优[16]。

本文提出了一种用于变电设备平稳信号及非平稳信号去噪的的蚁群优化小波阈值算法，该方法采用一种具有多阶连续导数的阈值函数，结合蚁群优化算法计算小波最优阈值进行去噪。对两种典型人工平稳信号、模拟局部放电信号及实测局部放电信号进行去噪试验。结果表明该算法能够有效抑制变电设备的状态信号中混叠的白噪声，相对于Donoho提出的标准软阈值法和文献[14]中的梯度迭代优化阈值方法，该算法更能从背景噪声中快速有效提取出变电设备状态信号，具有非常好的去噪效果和实用价值，有效实现了数字化变电站电气设备状态信号的快速处理。

2 蚁群优化小波阈值算法

假设序列Y={y0,y1,…,yN-1}和序列s={s0,s1,…, sN-1}分别为含噪信号的观测值和信号在i时刻的真实值，即:

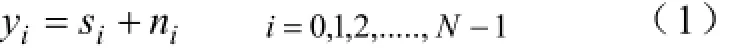
式中，ni为独立分布的高斯白噪声。小波去噪的目的是为了获得含噪信号Y的估计信号ŝ，并且使得ŝ与s的均方误差[10]最小。

根据参考文献[14]，梯度迭代优化阈值算法基本思想为:第t+1迭代次数的阈值λ(t+1)等于第t迭代次数的阈值λ(t)减去均方误差ξ(λ)函数梯度值△λ(t)，即:

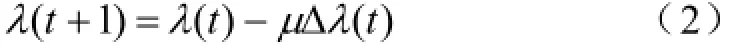
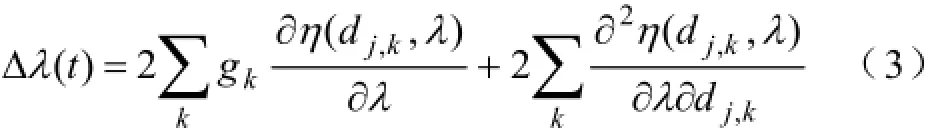
式中，μ为步长，根据参考文献[14]，△λ(t)如式（3）所示:式中，gk为函数估计表达式[14]，dj,k为j尺度上的小波细节系数。

由（3）可知，如采用Donoho提出的硬阈值函数和软阈值函数作为阈值函数，由于其导数不连续，无法进行自适应迭代，只能根据观测值有限序列Y估计阈值，因而它不是最佳阈值。

本文采用的阈值函数如式（4）所示[17]:

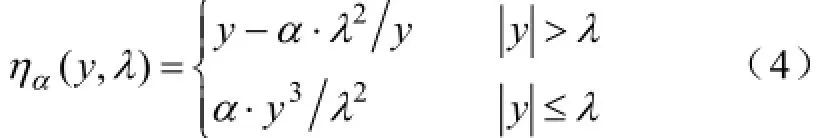
式中，α为一实数，文中α=0.5。

图1所示为硬阈值函数、软阈值函数及ηα(y, λ)阈值函数示意图，其一阶导数和二阶导数为式（5）和（6）:

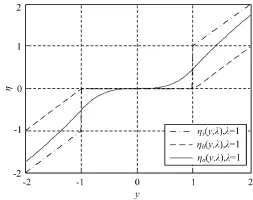
图1 不同阈值函数ηs(y, λ), ηh(y, λ) and ηα(y, λ)的比较Fig.1 Different thresholding functions of ηs(y, λ), ηh(y, λ) and ηα(y, λ)

将式（4）、（5）、（6）代入（2）、（3）就可以进行小波阈值的自适应迭代计算，并得出最优小波阈值。

由于变电设备状态信号包括一些非平稳信号，且这些信号（如局部放电信号等）的有效提取对变电设备的状态评估起着至关重要的作用。采用梯度迭代优化小波阈值方法进行去噪时难以得到理想的结果，且可能出现迭代计算难以收敛、计算时间花费大的情况，难以实际应用于变电设备状态信号处理中。文献[10]提出了用于局部放电去噪的粒子群算法优化小波自适应阈值法，粒子群算法搜索速度快、效率高，但其处理离散优化问题时容易陷入局部最优。因此，本文引入蚁群算法，对小波的阈值进行全局优化计算，使得阈值的获取快速而且准确。

蚁群优化（ant colony optimization，简称为ACO）算法是受自然界蚁群集体行为启发而提出的一种随机类搜索算法[18]。AOC算法具有较强的鲁棒性，其参数数目少，设置简单，易于应用到组合优化问题的求解，非常适合工程应用。AOC方法在求解问题时的主要操作过程如下所示[19]:设在第n次迭代过程中，蚂蚁k由城市p到q的概率(t)为:

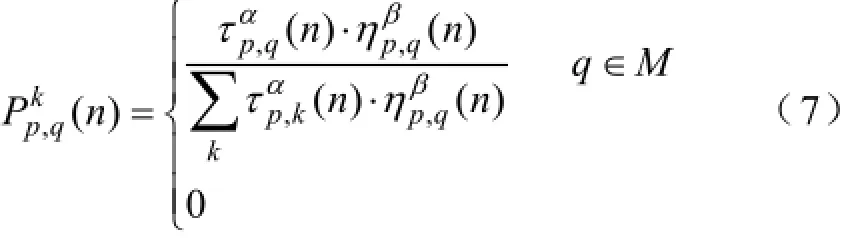
式中，M为蚂蚁k下一步允许选择的城市，τp,q为信息素，α为启发因子，用来表征信息的蓉重要程度，其中η=1/d，d为城市间的距离，β为期望因子，用来表征城市间距离的重要程度。

在蚁群完成1个循环后，对每条边上的信息素进行更新:

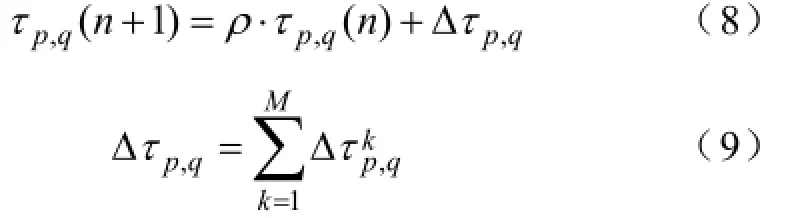
式中，ρ为信息素残留系数，且0≤ρ≤1，Δτp,q及Δτkp,q分别为蚁群与蚂蚁k在第n次迭代到第n+1次迭代过程中在边（p，q）上留下的信息素为:

式中，Q为常量，Lk为蚂蚁在本次循环中所选择路径的总长度。在蚁群算法中，参数Q、α、β、ρ的最佳组合可由试验确定。

蚁群优化小波自适应阈值方法的步骤如下所示:

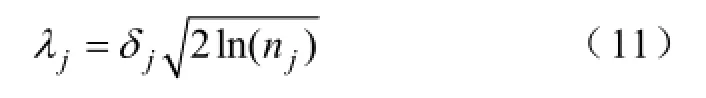
式中，λj为j尺度上的小波系数阈值，nj为j尺度上的小波细节系数的长度，σj=MAD(|dj,k|，0≤k≤2j-1-1)/q，MAD(·)为取中值函数，q根据经验可在0.4～1之间选取，通常取0.6745[13]。

第二步:初始化蚁群，在满足控制变量约束条件下随机赋予蚁群中每个蚂蚁的初始城市位置λk和初始信息素浓度τkp,q。

第一步:设定ACO算法中参数Q、α、β、ρ、蚁群的数量K、城市数目M、最大迭代次数nmax的数值，计算蚁群λ的最大值和最小值为λmax和λmin，当q取0.1和1，根据式（11）可得λmax和λmin。

第三步:根据式（3）确定每一蚂蚁的适应度值△λ(n)，当△λ(n)最小时，可认为λ达到最优值。

第四步:按式（7）逐代城市计算蚂蚁选择下一座城市的概率函数(1)，记录到访的城市及路线，完成各自蚂蚁的周游，根据最小距离保存最佳路线

第五步:根据式（8）、（9）和（10）更新蚁群中蚂蚁λk的信息素浓度。

第六步:判断ACO算法是否满足终止条件，若满足则输出最优值λopt，否则转入第三步循环计算，直至达到最大迭代次数，找到最佳路径，输出最优值λopt。

本文的ACO算法的参数设定如下:蚁群的数量K=40，城市数目M=50，最大迭代次数nmax=500。蚁群优化小波阈值去除信号中白噪声的计算基本流程如图2所示。

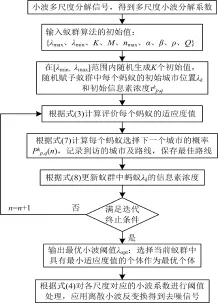
图2 蚁群优化小波阈值算法去噪计算流程图Fig.2 Flowchart of de-nosing using ACO wavelet threshold estimation

3 典型人工平稳信号去噪结果分析

变电设备状态信号存在着大量的平稳信号，如光电互感器、电子式互感器等输出的电压电流信号，由于其存在着谐波等其他干扰标准正弦信号会发生畸变，故本文选择两种典型人工平稳信号HeaviSine和Doppler信号模拟数字化变电站电气设备在线监测的平稳信号，所有仿真信号的长度为2048个点。采用Donoho提出的标准软阈值法(standard soft wavelet threshold estimation，简称为STE)、梯度迭代优化阈值算法（gradient-based threshold estimation，简称为GTE）及蚁群优化小波阈值算法（ant colony optimization threshold estimation，简称为ACOTE）对两种信号的去噪结果如图3-4所示。图3-4a是原始的仿真信号，图3-4b是局部放电仿真信号被信噪比等于1的白噪声污染后的信号，其中σs/σe=6，σs与σe分别为信号及噪声的标准方差。图3-4c是采用STE去噪后的结果，图3-4d是采用GTE去噪后的结果，图3-4e是采用ACOTE去噪后的结果。试验结果表明GTE及ACOTE算法能够有效去除白噪声的干扰，且能够保留更多的信号特征，STE方法几乎已不能提取Doppler信号的初始阶段信号。

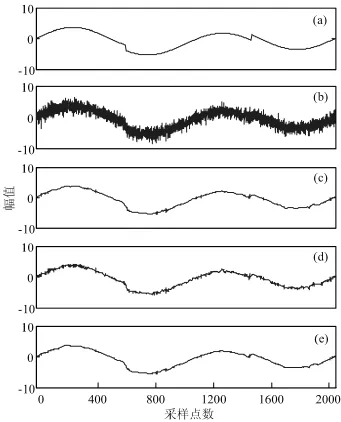
图3 HeaviSine信号去噪结果:(a)原始信号; (b) 染噪信号; (c-d) STE、GTE、ACOTE去噪结果Fig.3 The de-noised result of HeaviSine

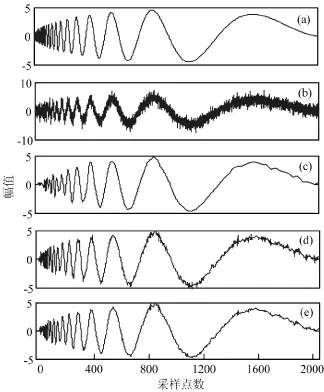
图4 Doppler信号去噪结果:(a)原始信号; (b) 染噪信号; (c-d) STE、GTE、ACOTE去噪结果.Fig.4 The de-noised result of Doppler

表1为上述三种去噪方法在MATLAB R2010a中的计算时间，结果表明GTE方法在计算过程中由于需要迭代求解，耗时较长，而ACOTE方法大大减少了小波阈值的优化计算时间。

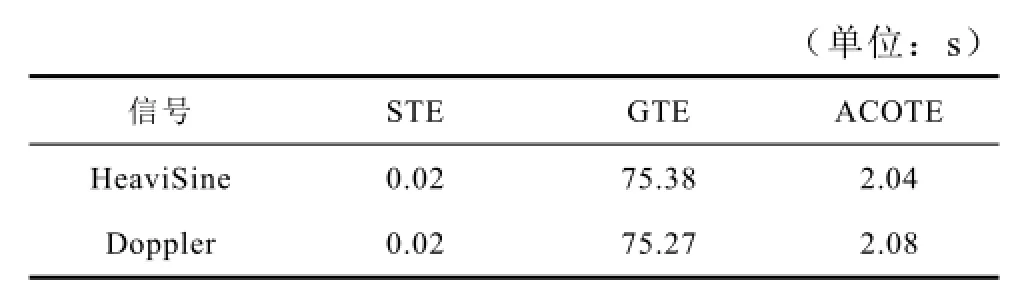
表1 三种去噪方法的计算时间Tab.1 Time cost of three method

3 局部放电信号去噪结果

3.1局部放电模拟信号去噪分析

数字化变电站的变电设备状态信号还存在着一些非平稳信号，其中局部放电脉冲是其中一种典型的短时的瞬态信号，局部放电在线监测宽频带测量系统可能测到的信号可采用衰减振荡脉冲s脉冲模拟，由式（12）表示:

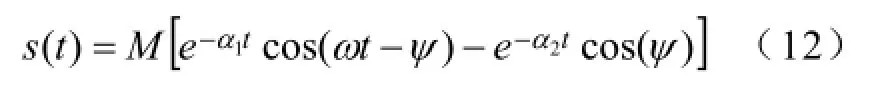
式中，M为信号幅值系数；α1和α2为衰减常数；ω = 2πf为振荡角频率，φ =arctan(ω/τ2)。

图5给出了局部放电仿真信号经两种去噪方法去噪后的效果图，其中仿真信号参数分别为M=1，α1=1×106s-1，α2=1×107s-1，f=1MHz，仿真采样率为60MS/s。图5a是原始的局部放电仿真信号s，图5b是局部放电仿真信号被信噪比等于1的白噪声污染后的信号，图5c-e分别为含噪局部放电信号采用STE、GTE及ACOTE方法去噪后的结果。局部放电去噪信号可用幅值误差及均方误差评价[10]，经三种去噪方法去噪后信号的计算结果如表2所示，结果表明采用GTE和ACOTE法去噪后的均方误差和幅值误差低于STE法，而ACOTE法去噪后信号的均方误差和幅值误差最小，其相对于原始信号的畸变率非常小。此外，STE、GTE及ACOTE方法的去噪时间分别为0.06、715.13及0.59s，可见ACOTE方法比GTE方法大大减少信号处理的时间，可以实现信号的实时有效传输。

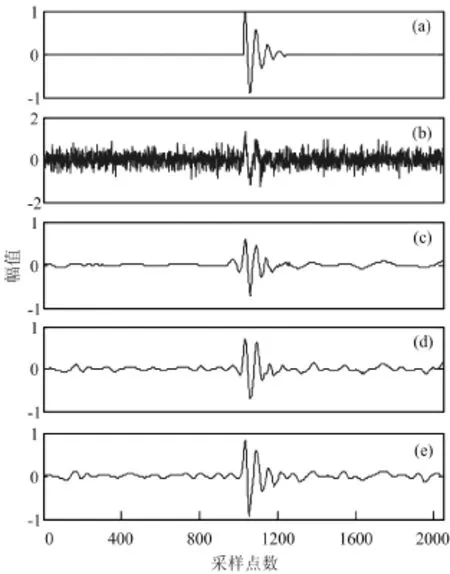
图5 局部放电信号去噪结果:(a)原始信号; (b) 染噪信号; (c-d) STE、GTE、ACOTE去噪结果.Fig.5 The de-noised result of PD signal：

表2 去噪信号幅值误差及均方误差Tab.2 Mean square error and magnitude error of de-noised signal

3.2实测局部放电信号去噪分析

图6所示为某110kV变电站1#主变压器局部放电带电检测系统实测的局部放电信号去噪结果。图6a为一个工频周期的局部放电信号，部分局部放电脉冲信号被背景噪声淹没。图6b和图6c分别为采用STE和ACOTE去噪的结果，GTE在去噪过程中难以收敛，故图中没有给出GTE方法的去噪结果。结果表明在原始信号中无法显示出的脉冲信号在采用STE和ACOTE方法去噪后显现出来了，并且采用ACOTE方法能够提取局部放电信号中的微弱信号。因此，在现场局部放电监测中如采用本文提出的ACOTE方法去除局部放电白噪声，能显著提高检测的灵敏度。

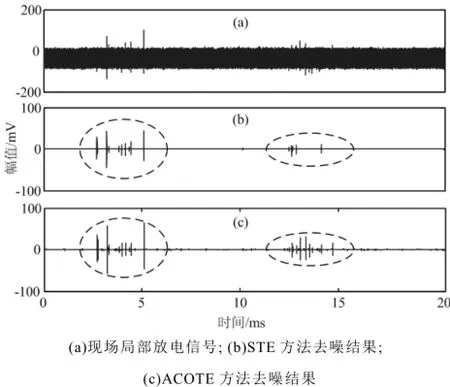
图6 现场局部放电信号去噪结果Fig.6 De-noised results of filed measured signal

5 结论

本文基于一种多阶连续可导阈值函数，结合蚁群优化算法，实现了变电设备状态信号去噪最优小波阈值的计算。采用标准软阈值方法、梯度迭代优化小波阈值算法及蚁群优化小波阈值算法对人工平稳信号以及局部放电信号进行去噪试验分析，得到的结论如下:

a）人工平稳信号的去噪结果表明，蚁群优化小波阈值算法及梯度迭代优化小波阈值算法比标准软阈值法能更有效的去除白噪声，但蚁群优化小波阈值算法大大缩短了小波阈值的优化计算时间。

b）对局部放电仿真信号的去噪结果表明，蚁群优化小波阈值算法比标准软阈值法及梯度迭代优化小波阈值算法能更有效的去除白噪声，同时还大大缩短了小波阈值的优化计算时间。

c）对含有强烈背景噪声的现场实测局部放电信号进行了去噪分析，结果表明梯度迭代优化小波阈值方法已不能收敛，而蚁群优化小波阈值方法能够有效提取出微弱局部放电脉冲。显示了该方法在数字化变电站电气设备状态信号处理应用中具有良好的去噪效果，有利于数字化变电站信号的快速、实时的网络通信。

[1] 曾庆禹, 李国龙. 变电站集成技术的发展——现代紧凑型变电站[J]. 电网技术, 2002, 26(8)： 60-67.

Zeng Qingyu, Li Guolong. Evolution of integrated technique of substation-modern compact substation[J]. Power System Technology, 2002, 26(8)： 60-67.

[2] 曾庆禹. 变电站自动化技术的未来发展二——集成自动化、寿命周期成本[J]. 电力系统自动化, 2000, 24(20)： 1-5.

Zeng Qingyu. The development of substation automation in the near feature part two¾Integrated automation, life cycle costs[J]. Automation of Electric Power Systems, 2000, 24(20)： 1-5. Ding Shuwen. Choosing internal communication network of digital substation integrated automation system[J]. Relay, 2003, 31(7)： 37-40.

[3] 董明, 严璋, 杨莉, 等. 基于证据推理的电力变压器故障诊断策略[J]. 中国电机工程学报, 2006, 26(1)： 106-114.

Dong Ming, Yan Zhang, Yang Li, et al. An evidential reasoning approach to transformer fault diagnosis [J]. Proceedings of the CSEE, 2006, 26(1)： 106-114.

[4] Jian Li, Tianyan Jiang, Stanislaw Grzybowski, et al. Scale Dependent Wavelet Selection for De-Noising of Partial Discharge Detection[J]. IEEE Transaction on Dielectrics and Electrical Insulation, 2010, 17(6)：1705-1714.

[5] U. Kopf, K. Feser. Rejection of narrow-band noise and repetitive pulses in on-site PD measurements[J]. IEEE Transaction on Dielectrics and Electrical Insulation, 1995, 2(6)： 433-446.

[6] 郭亮, 黄宏新, 成永红, 等. 嵌入式局部放电检测系统的数字滤波器设计[J]. 高电压技术, 2007, 33(8)： 44-47, 55.

Guo Liang, Huang Hongxin, Cheng Yonghong, et al. Design of digital filter used in embedded measuring system of PD[J]. High Voltage Engineering, 2007, 33(8)： 44-47, 55.

[7] 彭莉, 唐炬, 张晓星, 等. 一种基于复小波变换提取PD信号的分块自适应复阈值算法[J]. 电工技术学报, 2008, 23(7)： 112-117.

Peng Li, Tang Ju, Zhang Xiaoxing, et al. An algorithm of complex self-adaptive block threshold for extracting PD signal[J]. Transactions of China Electrotechnical Society, 2008, 23(7)： 112-117.

[8] 唐炬, 谢颜斌, 周倩, 等. 用于复小波变换去噪的复阈值构造算法[J]. 电工技术学报, 2008, 23(10)：121-128.

Tang Ju, Xie Yanbin, Zhou Qian, et al. Study of the construction of complex threshold for complex wavelet transform suppressing noise[J]. Transactions of China Electrotechnical Society, 2008, 23(10)： 121-128.

[9] 李化, 杨新春, 李剑, 等. 基于小波分解尺度系数能量最大原则的GIS局部放电超高频信号自适应小波去噪[J]. 电工技术学报, 2012, 27(5)： 84-91.

Li Hua, Yang Xinchun, Li Jian, et al. The maximum energy of wavelet decomposition approximation-related adaptive wavelet de-noising for partial discharge UHF pulse in GIS[J]. Transactions of China Electrotechnical Society, 2012, 27(5)： 84-91.

[10] 江天炎, 李剑, 程昌奎等. 粒子群优化小波自适应阈值法用于局部放电去噪[J]. 电工技术学报, 2012, 27(5)： 77-83.

Jiang Tianyan, Li Jian, Cheng Changkui, et al. Denoising for partial discharge signals using PSO adaptive wavelet threshold estimation[J]. Transactions of China Electrotechnical Society, 2012, 27(5)： 77-83.

[11] Jian Li, S. Grzybowski, Lin Du, et al. Extraction of partial discharges from noises by use of wavelet and pulse-sequence analysis[C]. 2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena, Kansas City Missouri, USA 2006： 656-659.

[12] 王晓蓉, 杨敏中, 董明, 等. 基于神经网络的局部放电脉冲特征参数选择方法[J]. 电工技术学报, 2002, 17(3)： 72-76.

Wang Xiaorong, Yang Minzhong, Dong Ming, et al. Method for the characteristic parameter selection of PD pulse based on neutral network[J]. Transactions of China Electrotechnical Society, 2002, 17(3)： 72-76.

[13] D. L. Donoho. De-noising by Soft-Thresholding[J]. IEEE Trans. on Information Theory, 1995, 41(3)：613-627.

[14] X. P. Zhang and M. D. Desai. Adaptive DenoisingBased on SURE Risk[J]. IEEE Signal Processing Letters, 1998, 5(10)： 265-267

[15] 李剑, 孙才新, 杨霁, 等. 局部放电在线监测中小波阈值去噪法的最优阈值自适应选择[J]. 电网技术, 2006, 30(8)： 25-30.

Li Jian, Sun Caixin, Yang Ji, et al. Adaptive optimal threshold selection of wavelet-based threshold denoising for on-line partial discharge monitoring[J]. Power System Technology, 2006, 30(8)： 25-30.

[16] 王伯成, 施锦丹, 王凯. 粒子群优化算法的研究现状与发展概述[J]. 电讯技术, 2008, 48(5)： 7-11.

Wang Bocheng, Shi Jindan, Wang Kai. Research status and review of the development of particle swarm optimization[J]. Telecommunication Engineering, 2008, 48(5)： 7-11.

[17] M. Nasri and H. Nezamabadi-pour. Image Denoising in the wavelet domain using a new adaptive thresholding function[J]. Neurocomputing, 2009, 72(4-6)： 1012-1025.

[18] 张良, 刘晓胜, 戚佳金等. 一种低压电力线通信改进分级蚁群路由算法[J]. 电工技术学报, 2014, 29(2)： 318-323.

Zhang Liang, Liu Xiaosheng, Qi Jiajin, et al. Study of improved hierarchical ant colony routing algorithm for low-voltage power line communication[J]. Transactions of China Electrotechnical Society, 2014, 29(2)：318-323.

[19] M. Dorigo, T. Stutzle. Ant Colony Optimization[M]. Bradford Books, 2004.

Extraction of Condition Signals of Electrical Plants by ACO Wavelet Threshold Estimation

Long Hongyu1 Zhang Xiaoyong2 Hu Xiaorui2 Feng Shanshan3 Li Long2
（1. Southwest University Chongqing 400715 China 2. Chongqing Electric Power Research Institute Chongqing 401123 China 3. Zhejiang Hangzhou yuhang Electric Power company Hangzhou 311100 China）

Based on the problem of the fast and effectively extraction for condition signals of electrical plants in digital substation, this paper presents an approach of ant colony optimization threshold estimation(ACOTE) for de-noising of partial discharge(PD) signals. A class of shrinkage functions with continuous derivatives based on the SURE algorithm and ACO algorithm are utilized for the threshold estimation. The ACO algorithm is competent to obtain the global optimum thresholds and to raise the efficiency of adaptive searching computation. For verifying the de-noising results, two methods of standard soft wavelet threshold estimation(STE) and gradient-based threshold estimation (GTE) are used for de-noising of two typical artificial stable signals, simulative PD signal and the field PD signal. The results show that the white noise can be removed effectively by the ACOTE, the distortion of which is smaller than the signals de-noised by the STE and GTE. Meanwhile, the ACOTE is a much less time-consuming scheme and exhibits a promising prospect in practical application.

Electrical plants; electrical detection; condition signal; wavelet de-noise; ant colony optimization algorithm.

TM411

龙虹毓 男，1979年生，博士，博士后，副教授，从事电气设备状态与系统运行可靠性研究。

2014-09-10

张晓勇 男，1981 年生，硕士，从事电力系统运行与检修研究。