新型模块组合式定子永磁电机

张炳义 贾宇琪 冯桂宏

新型模块组合式定子永磁电机

张炳义 贾宇琪 冯桂宏

（沈阳工业大学电气工程学院 沈阳 110870）

针对低速大功率电机体积过大带来的制造、运输、装配以及维护困难等问题，提出了一种基于采用不等跨距绕组的模块组合式定子永磁电机结构，实现了低速大功率电机定子的模块化制作，增强了电机的制造灵活性、运行可靠性、可维护性以及容错性。本文阐述了模块组合式定子永磁电机结构，总结了其设计方法，并对模块组合式电机定子分块规则和不等跨距绕组进行了研究。在此基础上设计制造了一台样机，采用有限元方法进行了仿真分析，并用解析法和增量电感法分别计算了样机的自感参数和互感参数。最后搭建试验台进行了实验。仿真结果和实验结果都验证了所提结构和设计方法的合理性。

低速大功率 模块化 永磁电机 不等跨距绕组 设计

1 引言

在矿山、石油、冶金、船舶推进以及风电等大型机械装备中，负载多具有低速大功率特点，其一般采用感应电机-减速机的驱动模式。减速机的存在会给传动系统带来效率降低、装备体积增大、振动和噪声加剧、润滑油渗漏污染以及日常维护工作量大等诸多弊端。此外，感应电动机的效率和功率因数与其负载率直接相关，各种机械装备都是按照极限能力选择电机额定功率，而实际运行中负荷都是变动的，因此力能指标常常会远低于额定值。近年来，采用低速大功率永磁电机直接驱动在此类机械装备中已经得到了越来越广泛的关注[1]。低速大功率电机一定具备低速大转矩电机的特点，而电机的转矩又与电机的有效体积成正比，因此低速大功率直驱永磁电机的体积势必很庞大。电机过大的体积会给其制造、运输、装配以及维护带来巨大的困难。

在大型电机设计方面，大多数文献都停留在对电机某方面性能计算、发热与冷却研究以及电机绕组的研究上，例如，文献[1]通过建立定子多风路通风系统三维流动与传热计算的数学模型，得出了各个径向通风沟内的流体速度、温度的空间分布情况；文献[2]建立了凸极效应永磁同步电机的径向电磁力波模型，对电机的电磁振动特性进行了研究；文献[3]则提出了一种最优弱磁路径控制策略，对内置式永磁同步电机的弱磁调速进行了研究；文献[4]通过有限体积法（FVM）对2.5MW永磁风力发电机进行了流体场和温度场的耦合求解，为风力发电机的温升计算和通风结构设计提供了依据；文献[5]是在对现有分块开关磁阻电机结构和磁路解析的基础上，提出了五种新型结构的分块开关磁阻电机；文献[6]对SVPWM供电下低速大转矩永磁同步电机的设计进行了研究；文献[7-8]则是对不同应用场合的分数槽绕组进行了研究。在电机制造方面，虽然也有较少文献对电机的模块化制造进行了研究，但只适用于分数槽集中绕组，对电机设计中普遍采用的其它结构形式绕组却不适用。例如，文献[9]提出了一种模块式风力发电机结构，但其是通过采用集中绕组的单齿模块拼接实现；文献[10]对模块化级联电机采用分数槽集中绕组进行了研究，结果表明该方法能有效减小电机体积，提高其转矩密度。

为此，本文提出了一种基于采用不等跨距绕组的低速大功率模块组合式定子永磁电机结构（Low-Speed and High-Power Permanent Magnet Synchronous Machine with Module Combination Stator，LSHPMCSPMSM），实现了交流电机定子的模块化制作。从一定程度上能够缓解大型交流电机定子过大带来的相关问题，增强了电机的制造灵活性、运行可靠性、可维护性以及容错性。本文在阐述LSHPMCSPMSM结构的基础上，总结了其设计方法，并研究了定子分块规则与不等跨距绕组结构。在此基础上，设计制造了一台样机，采用有限元仿真分析证明了样机设计的合理性，并采用解析法和增量电感法分别计算了样机的自感参数和互感参数。最后采用静测法对样机进行了电感参数测试，搭建试验台对电机不同转速下投入不同模块个数时的效率进行了实验。

2 LSHP-MCSPMSM基本结构

LSHP-MCSPMSM定子结构如图1所示，电机定子由数个定子单元模块组成，转子结构与常规永磁电机转子结构基本相同。为了能够形成三相对称绕组，每个定子扇形块内钱放着具有大、小两种规格跨距的不等跨距绕组。

图1 模块组合式定子结构结构图Fig.1 Structure of LSHP-MCSPMSM

3 LSHP-MCSPMSM设计研究

3.1LSHP-MCSPMSM定子分块规则

对于分数槽绕组，每极每相槽数q总能写成（整数槽绕组可以认为是一种特殊的分数槽绕组，故也包含在内）

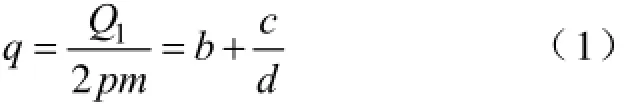
其中，m为相数；Q1为定子槽数；p为极对数；b为整数；c/d为不可约的真分数；要形成三相对称绕组，需满足d≠3n，n∈N+。

在三相电机中，当q为分数时，则每个极距内和每个相带内的槽数就不是整数。一般情况下，分数槽电机的定子槽数Q1和极对数p存在一个最大的公约数，即

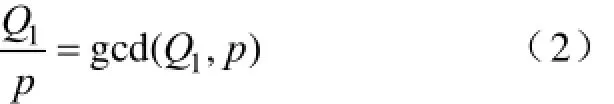
式中，gcd(Q1,p)为电机定子槽数与极对数的最大公约数。令Q0=Q1/gcd(Q1,p)，p0=p/gcd(Q1,p)，则q又可写成

式（3）意味着在分数槽绕组的电机中，每2p0个磁极下每相占有Q0/m个槽电机的齿槽分布、感应电动势向量图和磁动势向量图，以2p0个磁极为一个周期，重复gcd(Q1,p)次。其中，Q0就是在对应每极每相槽数q下能形成一个单元电机模块需要的最少槽数。因此，LSHP-MCSPMSM定子的分块规则为:对于一个定子槽数为Q1、极对数为p的电机，整个电机定子最多可分得的单元模块个数为gcd(Q1,p)；电机能引出的最多并联支路数也为gcd(Q1,p)；对于LSHP-MCSPMSM，可以选择不大于gcd(Q1,p)个单元模块进行组装拼接来形成电机定子。另外，考虑到单边磁拉力对电机运行性能和轴承寿命的影响，应尽量把定子单元模块拼装在圆周的对称位置。

与采用集中绕组的电机分块制造的显著区别在于，上述给出的定子分块规则适用于每极每相槽数q为任何值的双层叠绕组。值得说明的是，当每极每相槽数q选为0.4时，绕组一般采用集中绕组，即直接在齿上绕制，此时电机定子可由多个单齿模块组合而成，因此不受单个模块最少槽数的限制。

3.2不等跨距绕组结构

同步电机的运行原理是通过电枢绕组产生的旋转磁场与转子磁极相互作用产生来电磁转矩。其中，绕组在定子槽内与气隙相对的直线部分是能量转换的核心，而绕组端部连接部分仅仅起到维系电流连续的作用。正是基于这点，提出了不等跨距绕组结构。相比于常规双层叠绕组，不等跨距绕组结构只是改变了绕组部分线圈端部的连接方式，而绕组在槽内的直线部分排布与常规双层叠绕组保持完全一致，不会影响电机内部的机电能量转换过程。

采用不等跨距绕组结构，通过大跨距线圈反向嵌放的方法完成单个定子单元模块内三相绕组的独立放置，不同单元模块间的完全相同且相互独立，不等跨距绕组如图2所示。

图2 不等跨距绕组结构图Fig.2 View of Unequal span winding

考虑到线圈节距选为(1-1/υ)τ时（τ为电机极距），可以有效的消除第υ次谐波。因此，电机设计中绕组节距通常选为(5/6)τ来同时削弱5、7次谐波。综上，对于不等跨距绕组中两种规格线圈跨距的选取需满足以下条件:

小跨距线圈节距为

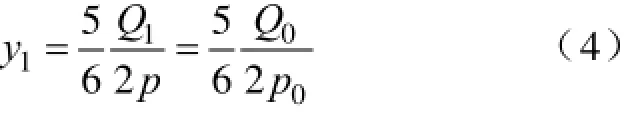
大跨距线圈节距为

式中，Q1为定子槽数；Q0为单元模块电机需要的最少槽数；p为电机极对数；p0为单元模块电机的极对数；k为组成独立模块所需的最少槽数电机模块的个数。

另外，小跨距线圈的节距即为每条支路每相绕组中大跨距线圈的个数。小跨距线圈节距的选取会引起采用不等跨距绕组电机的每条支路每相绕组中串联的大、小跨距线圈数量的不一致，进而对电机绕组的对称性和绕组电流相位的对称性产生影响。因此，考虑到三相绕组的对称性，应优先选用小跨距线圈跨距y1为3或者3的倍数的方案。

3.3LSHP-MCSPMSM设计方法

常规的直线电机和旋转电机都有国家标准和相应的电机设计程序作为参考，而本文提出的LSHPMCSPMSM是一种非标准电机，因此很有必要对其设计方法进行深入的研究。本文在研究定子分块规则和不等跨距绕组的基础上，总体设计方法采用单元电机的思路，即将每个定子单元模块和转子分别看作一台单元电机，整台电机可以视为由多台单元模块电机共同拼接组成。利用集零为整的思想，首先采用经典的等效磁路计算方法，将多台单元模块电机等效为一台普通的旋转电机进行设计，然后再利用有限元方法对电机的结构参数进行分析和优化，得到理想的方案后再把整台电机定子分成若干个单元模块电机，最后选择其中的几块进行组装。另外，考虑到永磁材料性能与温度息息相关，而传统的电机设计程序中缺乏对温升的循环校验，为此，本文提出的设计方法中在传统永磁电机设计基础上又引入了温度循环。综上，总结出了LSHP-MCSPMSM的设计方法，设计流程如图3所示。

图3 LSHP-MCSPMSM设计流程图Fig.3 Design flow chart of LSHP-MCSPMSM

4 样机设计与分析

4.1样机设计

为了验证如前所述的模块组合式永磁电机定子分块规则的正确性以及不等跨距绕组对电机性能的影响，研制了一台定子72槽、30极，并且转子采用表贴式磁极结构的样机。同时，每极每相槽数q选为0.8，以解决电机转速低、极数多以及受定子冲片外径限制槽数又有限的矛盾。根据前面给出的单元模块槽数与电机极数、槽数关系，有:gcd(Q1,p)= gcd(72, 15)=3；Q0=Q1/gcd(Q1,p)=72/3=24；这样，整个样机定子最多可分成3个独立模块；电枢绕组最多可分为3路引出，即每个定子单元模块单独引出一条支路，样机定子模型如图4所示。

图4 样机定子模型Fig.4 Model of LSHP-MCSPMSM stator

电机定子绕组采用了不等跨距绕组，设计出的小跨距线圈跨距y1=2，大跨距线圈跨距为Y1=22。显然，单元模块内的每相仅由一条支路构成，每条支路中8个线圈串联。由于小跨距线圈跨距为2，不是3的整数倍，因此每条支路中各相大、小跨距绕组线圈的构成个数不等，其中A相和C相下每条支路均由7个小跨距线圈和1个大跨距线圈组成，B相下每条支路则完全是由8个小跨距线圈构成。综上，设计出样机的主要参数如表1所示。

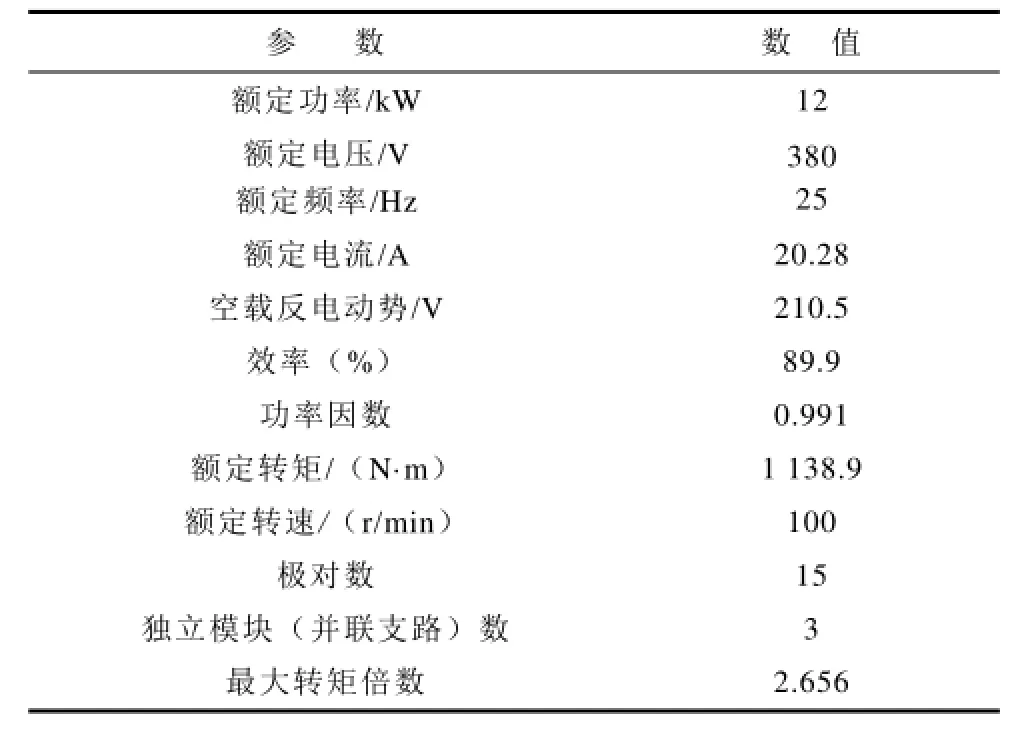
表1 样机主要参数Tab.1 Primary parameters of the sample

另外，鉴于该种类型电机大多应用在像水轮发电机等立式安装的场合，因此样机决定做成立式机壳。

4.2样机仿真分析

针对上述设计出的样机，利用有限元软件建模进行了仿真分析。结果如图5～图7所示。

图5 样机空载磁场分布Fig.5 The magnetic field distribution map of motor with no-load

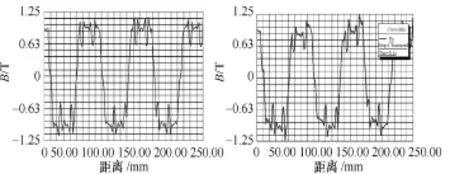
图6 样机空载、负载气隙磁密波形Fig.6 The air-gap flux density wave of motor with no-load and full-load

图7 样机空载、负载反电动势波形Fig.7 The EMF wave of motor with no-load and full-load

5 不等跨距绕组对电机性能影响分析

LSHP-MCSPMSM的各个单元模块都完全相同，所以先考虑一条支路中三相绕组电感计算。对于不等跨距绕组电感的计算，主要是对大、小两种规格跨距线圈的电感计算。电感参数分为自感和互感两种，自感参数可以通过解析法近似求得，而对于采用不等跨距绕组的定子端部交叠复杂，采用解析法精度很难保证，因此，互感参数的计算通过有限元方法求取。

5.1自感计算

基于等效磁路采用集中参数解析法计算绕组自感，通常先分别求取主电感、槽漏感和端部漏感，然后得到一个线圈的自感，最后根据线圈之间的耦合关系计算一相绕组的自感。

5.1.1 主电感的计算

主电感对应的磁力线从定子穿过气隙，然后经由转子再匝链回来。其计算公式为

式中，μ0为真空磁导率；N为线圈的匝数；l为线圈所处铁心的有效轴向长度；Q1为电机的定子槽数；k为线圈所包含的齿数（常规线圈等于2，大跨距线圈等于22）；τt为电机的齿距；hm为永磁体磁化方向上的长度；μr为永磁体的相对磁导率；kc为卡特系数。

根据文献[12]有

5.1.2 槽漏感的计算

单层绕组的槽漏感的大小取决于槽型结构，双层绕组的槽漏感除了取决于槽型结构还取决于上下层绕组流过电流的相位[13]。而大跨距线圈在槽内的有效导体流过的电流相位与常规线圈是一样的。所以常规线圈与大跨距线圈的槽漏感是一样的。双层短距绕组梨形槽漏感计算公式为:

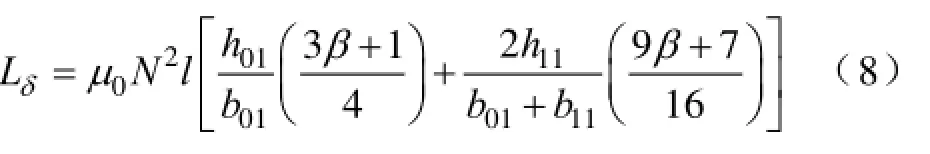
式中，β=5/6，为短距系数。

5.1.3 端部漏感的计算

绕组端部漏感是对应绕组端部匝链的漏磁场的电感。不等跨距绕组中的小跨距线圈和大跨距线圈的端部形状不同，需要分开来计算。由于电机绕组端部形状复杂，通常采用含有经验校正系数的经验公式来计算电机的绕组端部漏感。

文献[14]给出绕组端部漏感的计算公式为

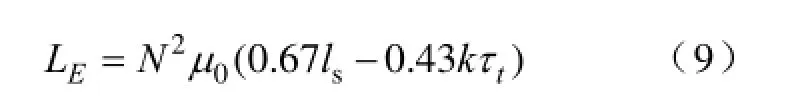
式中，ls为线圈的端部长度。

[15]给出了端部长度的计算方法，计算得到小跨距线圈的端部长度为ls=75.11mm，大跨距线圈的端部长度为ls=526.21mm。

最终单个线圈的自感为上述3个电感之和，计算得到。

小跨距规格线圈自感为

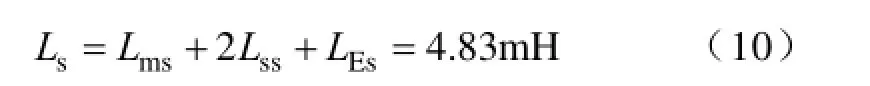
大跨距规格线圈自感为

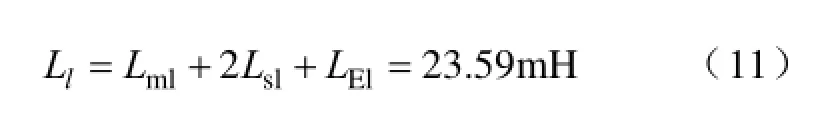
5.2互感计算

线圈的互感与线圈的自感一样，线圈的互感也包括主电感、槽漏感和端部漏感三部分。对于不等跨距绕组来说，由于采用大跨距线圈，端部交叠比较复杂，采用解析法计算线圈的互感比较复杂，且计算精度不能保证，因而采用有限元法计算互感。具体为首先计算磁链，然后按照增量电感的定义来求取非线性增量电感，其具体过程为:

（1）按照不等跨距定子结构建立样机的计算模型，剖分结果如图8所示。有限元分析得到转子精致时各位置的磁链变化，并存储每一步的数据文件。

图8 样机模型剖分结果Fig.8 Mesh result of the model machine

（2）用计算得到的单位电流下的磁链减去零电流下的磁链，则剩下的磁链结果就是单独由电流产生的磁链。根据增量电感的定义，将剩余磁链除以绕组电流，则可求出该转子位置出线圈的互感。计算公式为

式中，Ψ1为永磁体单独作用1号线圈匝链的磁链；Ψ2为1号线圈通入电流I后2号线圈匝链的磁链。

按照上述分析流程，分别对样机一条支路上大跨距线圈的自感、小跨距线圈的自感、大跨距线圈和小跨距线圈之间的互感以及小跨距线圈之间的互感进行计算，结果如图9所示。

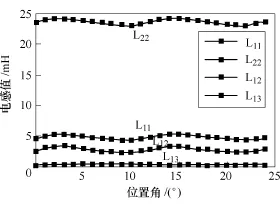
图9 线圈的自感和互感Fig.9 Self-inductance and mutual-inductance curves of the coils

图中，L22为大跨距线圈的自感，L11为小跨距线圈的自感，L12为大跨距线圈与小跨距线圈之间的互感，L13为两个小跨距线圈之间的互感。可以看出，是由于永磁体产生的磁场引起的饱和效应，线圈的电感不为恒值，小跨距线圈与大跨距线圈的自感平均值分别为5.3mH和24.5mH，与磁路法计算值接近。使用此方法求出了一条支路上所有的线圈的自感和互相之间的互感，考虑线圈之间的关系，按照线圈的平均值求出一条支路的三相绕组的相自感，如表2所示。

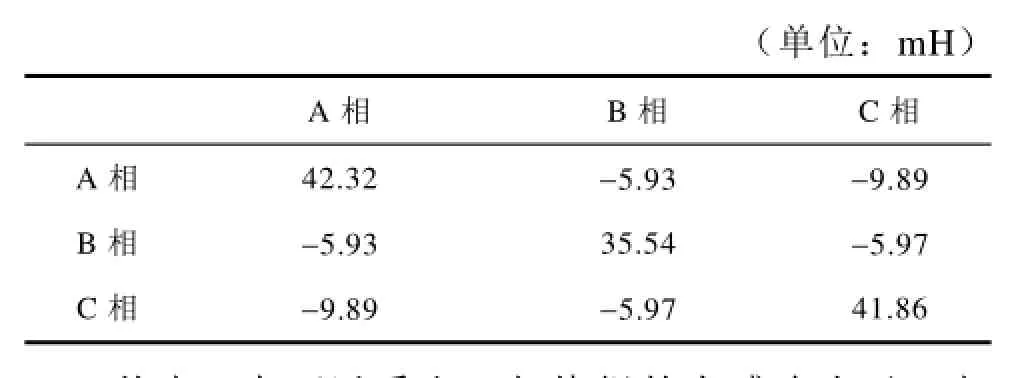
表2 样机电感参数Tab.2 Inductance parameters of three-phase winding

从表2中可以看出B相绕组的自感略小于A相与C相绕组的自感值，这是由B相绕组没有大跨距线圈引起的。

5.3 不等跨距绕组电感参数对电机性能的影响

根据表2，求得

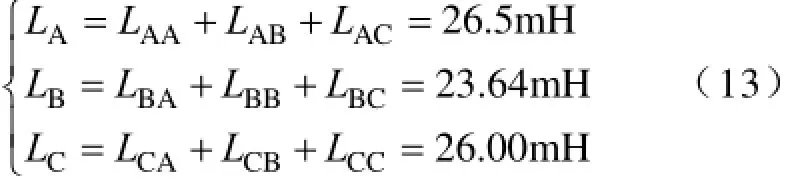
常温下，用万用表测得样机每条支路A、B、C三相的电阻分别为2.70Ω、2.267Ω、2.70Ω。由此，得到样机每条支路A、B、C三相的阻抗分别为

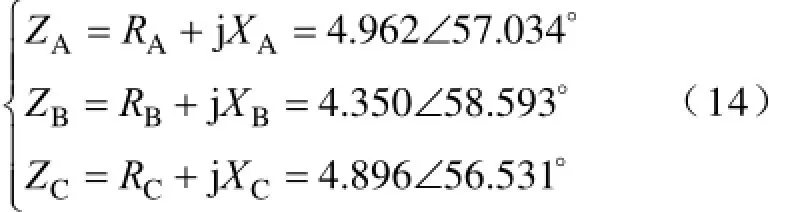
相量法作为线性正弦稳态电路分析的一种简便而有效方法，本文将采用该方法对采用不等距绕组样机的电流进行相位分析。根据永磁同步电动机相量图，可知

空载时，假设电机的功角为0°，即保证U˙和0E˙在相位上保持一致，并且电机通入电源为理想的三相对称电源。根据式（15）计算得到三相绕组的空载电流分别为

此时，ΦBA=118.441°、ΦCB=122.062°、ΦAC= 119.497°。

同理，可以分析电机带额定负载时的情况。

由以上分析可以看出，样机由于采用了不等跨距绕组，每相绕组的电感参数不再完全对称，因而造成了电机三相电流有效值不再相等，同时相位也出现了一定的偏移。

因此，电机在采用不等跨距绕组后，大跨距线圈的存在会引起每相绕组电感参数的不平衡。当该结构用在电动机中，这种不平衡会导致电机三相绕组产生的不再是圆形旋转磁场，损耗增加；用在发电机中，除了会引起损耗增加外，还会导致发电机发出的电不再是完全对称的三相交流电。针对此问题，在不等跨距绕组设计中可以通过如下两种方法消除大跨距线圈对电机绕组电感参数的影响:

（1）不等跨距绕组设计中，小跨距线圈节距尽量选取为3或者3的整数倍。此方法可以保证电机每条支路每相绕组中所包含的大、小跨距线圈数量一致，进而消除大跨距线圈对电感的影响。

（2）当小跨距线圈节距不为3或者3的整数倍时，可以通过在大跨距线圈少的相绕组中外接一个相应的电感，实现三相绕组电感参数的一致，进而消除每条支路每相绕组中包含大跨距线圈数量不等而引起的电感参数不平衡现象。

6 样机实验

6.1电感参数测试

对于样机采用的表面凸出式转子结构属于隐极电机，由于永磁体磁导率与空气非常接近，理论上认为其定子绕组的自感和互感与转子位置角无关，基本保持恒值。但是实际中，由于永磁体产生磁场对磁路饱和程度造成的影响，表面凸出式永磁电机也会表现出一定程度的凸极效应。本文利用静测法对不等跨距绕组的电感进行测量，在测试过程中使转子转速保持为零。由于磁场在铁心中产生的饱和效应使得该样机的电感会随着转子位置角的变化而变化。故在电感测试时，需要测试样机不同转子位置时的电感。具体操作方法是在电机轴伸端装上一个具有等分刻度的简易刻度盘，每格刻度为10°。转子每转动一刻度测量一次，通过计算该样机的周期是240电角度。所以测试的过程中只需转动24个刻度。样机实验平台如图10所示。

图10 样机试验台Fig.10 The test-bed of model machine

实验时给样机A相通电，通过调压器调节电压为7.6V。从简易分度盘的零刻度位置开始转动转子，分别记录转子不同位置时A、B、C三相绕组的端电压及A相电流。自感和互感计算公式为

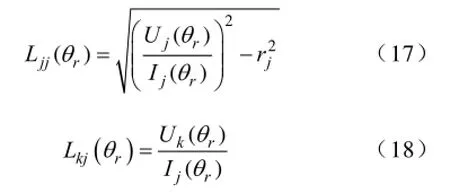
式中，rj为第j号线圈的电阻值。

经过试验数据的处理，得到的绕组的自感和互感随转子位置角变化的曲线分别如图11和图12。

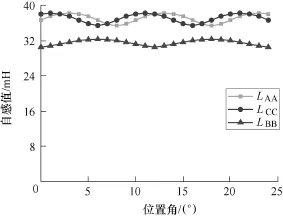
图11 三相绕组的自感实验曲线Fig.11 Experimental curves of three-phase winding self-inductance

由图11和图12可以看出样机定子绕组的电感在一个电周期的范围内变化了两个周期。并且，存在大跨距线圈相绕组的自感要大于不存在大跨距线圈相绕组的自感，存在大跨距线圈相绕组与不存在大跨距线圈相绕组之间的互感要大于不存在大跨距线圈相绕组之间的互感，与前面分析一致。另外，由于样机定子铁心轴向长度为225mm，线圈在定子槽内的直线部分与端部长度相差较小，因此引起了存在大跨距线圈相绕组的自感和互感与不存在大跨距线圈相绕组的自感和互感相差较大。而该种模块组合式定子结构主要应用在大型电机场合，因此实际中，大跨距线圈端部漏感的影响将会很小。

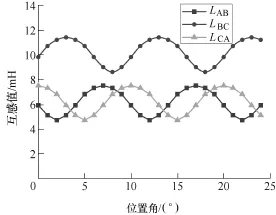
图12 三相绕组的互感实验曲线Fig.12 Experimental curves of three-phase winding mutual-inductance

6.2空载反电动势测试

由于样机转矩较大，采用反拖法测量空载反电动势波形有一定的困难。因此，本文充分利用样机多支路的特点，采用样机单条支路或者两条支路通电维持电机空载运行，在另一条开路支路测取电机的空载反电动势波形，测试结果如图13所示。

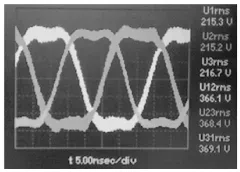
图13 样机空载反电动势波形Fig.13 The no-load EMF wave of motor

从图13看出，样机实测的空载反电动势波形与有限元仿真结果吻合良好。样机空载反电动势的设计值为210.5V，实测为215.3V，误差为2.28%。

6.3负载实验

采用变频器供电，对电机进行了负载实验。样机定子分为3个独立模块，每个模块单独构成一条支路。其额定转矩为1 138.9N·m，因此每个模块的额定转矩为1 138.9/3N·m=379.6N·m。由于样机是变频电机，因此除了测取额定转速下的负载特性曲线外，还需要测取其他转速下的负载特性曲线。实验中，利用变频器的压频比控制方式，分别测取了样机在供电频率分别为15Hz、20Hz和25Hz（相应的电机转速分别为60r/min、80r/min、100r/min）三种情况下负载由1.2TN降到空载的性能参数。并且每种供电频率下又分别对样机单个模块投入、2个模块投入以及3个模块全部投入三种情况进行了测试。测得的样机不同转速下不同数量模块投入时效率随负载率变化关系如图14、图15所示。

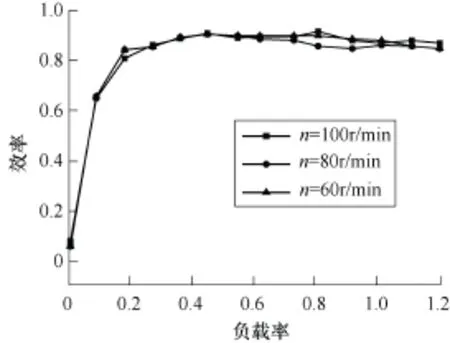
图14 不同转速下3模块全投入样机效率随负载率变化曲线Fig.14 The efficiency curve with load rate of the model machine with three modules running at different speed

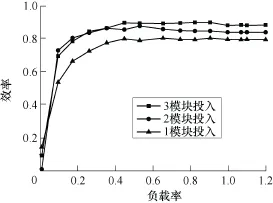
图15 额定转速下不同模块投入样机效率曲线Fig.15 The efficiency curve of different modules running at rate speed

从图14可以看出，由于新型模块组合式定子结构永磁电机运行在恒转矩区间，因此转速对其效率的影响很小。从图15可以看出，当电机运行于某一固定转速时，3个模块全部投入运行时电机的效率最高，2个模块投入运行时效率次之，单个模块运行时电机的效率最低。究其原因，不难发现是由于电机铁耗、机械损耗、杂散损耗（这三种损耗统称为电机的不变损耗，即不管电机运行于何种工况，其大小都近似保持恒定）等引起的。由于电机的输入电功率与模块数成正比，因此不变损耗占电机输入电功率的比例会随着投入模块数的减少而增加，这就造成了电机效率随着投入模块减少而降低，理论分析与实验结果相吻合。

7 结论

针对低速大功率电机过大的体积给其制造、运输、装配以及维护带来困难等问题，提出了一种基于采用不等跨距绕组的LSHP-MCSPMSM结构，实现了低速大功率交流电机定子的模块化制作，增强了电机的制造灵活性、运行可靠性、可维护性以及容错性。本文首先阐述了LSHP-MCSPMSM的结构，总结了其设计方法。通过在常规永磁电机设计程序的基础上引入温度循环，能很好的考虑温度对永磁体性能的影响。并对模块组合式电机定子分块规则和不等跨距绕组进行了研究。在此基础上设计制造了一台12kW样机，采用有限元方法进行了仿真分析，并用解析法和增量电感法分别计算了样机的自感参数和互感参数，最后搭建试验台进行了实验。仿真结果和实验结果都验证了所提结构和设计方法的合理性。对于这类电机，由于不变损耗的影响，当电机运行于某个固定转速时，电机的效率会随模块投入数量的增加而升高。绕组中大跨距线圈的存在会在一定程度上引起电机电抗参数的不对称，但是这种影响在大型电机中是很小的，可以忽略。本文研究内容为LSHP-MCSPMSM设计提供了一定的参考依据。

参考文献

[1] 李伟力, 杨雪峰, 顾德宝, 等. 多风路空冷汽轮发电机定子内流体流动与传热耦合计算与分析[J]. 电工技术学报, 2009, 24(12): 24-31.

Li Weili, Yang Xuefeng, Gu Debao, et al. Calculation and analysis of fluid flow and heat transfer of aircooled turbo-generator with multipath ventilation[J]. Transactions of China Electrotechnical Society, 2009, 24(12): 24-31.

[2] 张磊, 高春侠, 张加胜, 等. 具有凸极效应的永磁同步电机电磁振动特性[J]. 电工技术学报, 2012, 27(11): 89-96.

Zhang Lei, Gao Chunxia, Zhang Jiasheng, et al. Electromagnetic vibration characteristics of PMSMs with salient effect[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 89-96.

[3] 白玉成, 唐小琦, 吴功平. 内置式永磁同步电机弱磁调速控制[J]. 电工技术学报, 2011, 26(9): 54-59.

Bai Yucheng, Tang Xiaoqi, Wu Gongping. Speed control of flux weakening on interior permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 54-59.

[4] 丁树业, 孙兆琼. 永磁风力发电机流场与温度场耦合分析[J]. 电工技术学报, 2012, 27(11): 118-124.

Ding Shuye, Sun Zhaoqiong. Investigation of fluid field and thermal field coupled for permanent magnet winding generator[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 118-124.

[5] 陈小元, 邓智泉, 王小琳, 等. 分块开关磁阻电机的研究现状及其新结构构想[J]. 电工技术学报, 2011, 26(3): 20-28.

Chen Xiaoyuan, Deng Zhiquan, Wang Xiaolin, et al. Current status and new configurations of segmented switched reluctance machines[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 20-28.

[6] 张炳义, 冯桂宏, 王凤翔, 等. SPWM电源供电下低速大扭矩永磁同步电动机设计研究[J]. 电工技术学报, 2001, 16(6): 85-90.

Zhang Bingyi, Feng Guihong, Wang Fengxiang, et al. Study on low speed and high torque PMSM design with SPWM power supply[J]. Transactions of China Electrotechnical Society, 2001, 16(6): 85-90.

[7] Ayman M E, Thomas M J. Optimal flux weakening in surface PM machines using fractional-slot concentrated windings[J]. IEEE Transactions on Industry Applications, 2005, 41(3): 790-800.

[8] 安忠良. 模块式变速恒压混合励磁风力发电机设计研究[D]. 沈阳: 沈阳工业大学, 2011.

[9] 韩守亮, 崔淑梅, 王铁成, 等. 分数槽集中绕组永磁电机在模块化级联电机系统上的应用[J]. 电工技术学报, 2013, 28(3): 9-16.

Han Shouliang, Cui Shumei, Wang Tiecheng, et al. Application of fractional-slot concentrated winding permanent magnet machines in modular cascade machine system[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 9-16.

[10] 张炳义, 贾宇琪, 李凯, 等. 一种表贴式永磁电机磁极结构优化研究[J]. 电机与控制学报, 2014, 18(5): 43-48.

Zhang Bingyi, Jia Yuqi, Li Kai, et al. Study onmagnetic pole structure of surface mounted PMSM[J]. Electric Machines and Control, 2014, 18(5): 43-48.

[11] 王骞, 邹继斌, 赵玫. 横向磁场永磁直线电机结构及电感参数分析[J]. 电机与控制学报: 2010, 14(11): 37-43.

Wang Qian, Zou Jibin, Zhao Mei. Analysis of structure and inductance on a transverse flux Permanent magnet linear machine[J]. Electric Machines and Control, 2010, 14(11): 37-43.

[12] Gieras J F, Wing M. Permanent magnet motor technology[M]. New York: Marcel Dekker, 2002.

[13] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 2002.

[14] Hendershot J R, Miller The. Design of brushless permanent magnet motor[M]. Oxford: Clarendon Press, 1994.

[15] G Krebs, A Tounzi, B Pauwels. Modeling of a linear and rotary permanent magnet actuator[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4357-4360.

[16] 杨玉波, 王秀和, 丁婷婷. 基于单一磁极宽度变化的内置式永磁同步电动机齿槽转矩削弱方法[J]. 电工技术学报, 2009, 24(7): 41-45.

Yang Yubo, Wang Xiuhe, Ding Tingting. Different pole-arc width combination for reducing cogging torque of interior-magnet PMSM[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 41-45.

[17] 陈世元, 黄世鹏. 交流电机的绕组理论[M]. 北京:中国电力出版社, 2009.

[18] 常九健. 基于弧形电机拼接的大型望远镜驱动技术研究[D]. 北京: 中国科学院大学, 2013.

[19] Chang Jiujian, Ma Wenli, Huang Jinlong. Design and optimization of arc permanent magnet synchronous motor used on large telescope[J]. IEEE Transactions on Magnetics, 2012, 48(5): 1943-1947.

[20] Chang Jiujian, Wen Lima, Yong Kun Fan, et al. New methods for arc permanent magnet linear synchronous motor to decrease torque ripple[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2659-2663.

Novel Permanent Magnet Synchronous Machines with Modules Combination Stator

Zhang Bingyi Jia Yuqi Feng Guihong
（Shenyang University of Technology Shenyang 110870 China）

Aiming at the large volume of low-speed and high-power machines bringing the problems of manufacturing, transportation, installation and maintenance difficulties, a permanent magnet synchronous machine with modules combination stator based on unequal span winding was proposed. This structure achieves modular manufacturing of low-speed and high-power machines, and enhances the manufacturing flexibility, operation reliability, maintenance and fault tolerance. This paper describes the structure of the permanent magnet synchronous machines with modules combination stator, and its design method was summarized. Meanwhile, the partitioning principle and q selection method was studied. On this basis, a prototype machine was designed, and the simulation analysis was carried on by using the finite element method. At the same time, the self-inductance and mutual-inductance parameters of prototype were calculated by analytical method and incremental inductance method respectively. Finally, a test-bed of model machine was built to carry out the experiment. The simulation and experimental results were presented to verify the rationality of proposed structure and design method.

LSHP, modules combination stator, PMSM, unequal span winding, design

TM351

张炳义 男，1954年生，教授，博士生导师，主要研究方向为特种电机及其控制。

国家自然科学基金(51177106)和国家重大科学仪器设备开发专项（2012YQ05024207）资助项目。

2014-10-09

贾宇琪 男，1988年生，博士研究生，研究方向为特种电机及其控制（通讯作者）。